人教版九年级数学上册第二十三章旋转复习学案含答案
文档属性
| 名称 | 人教版九年级数学上册第二十三章旋转复习学案含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 225.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 20:23:32 | ||
图片预览

文档简介
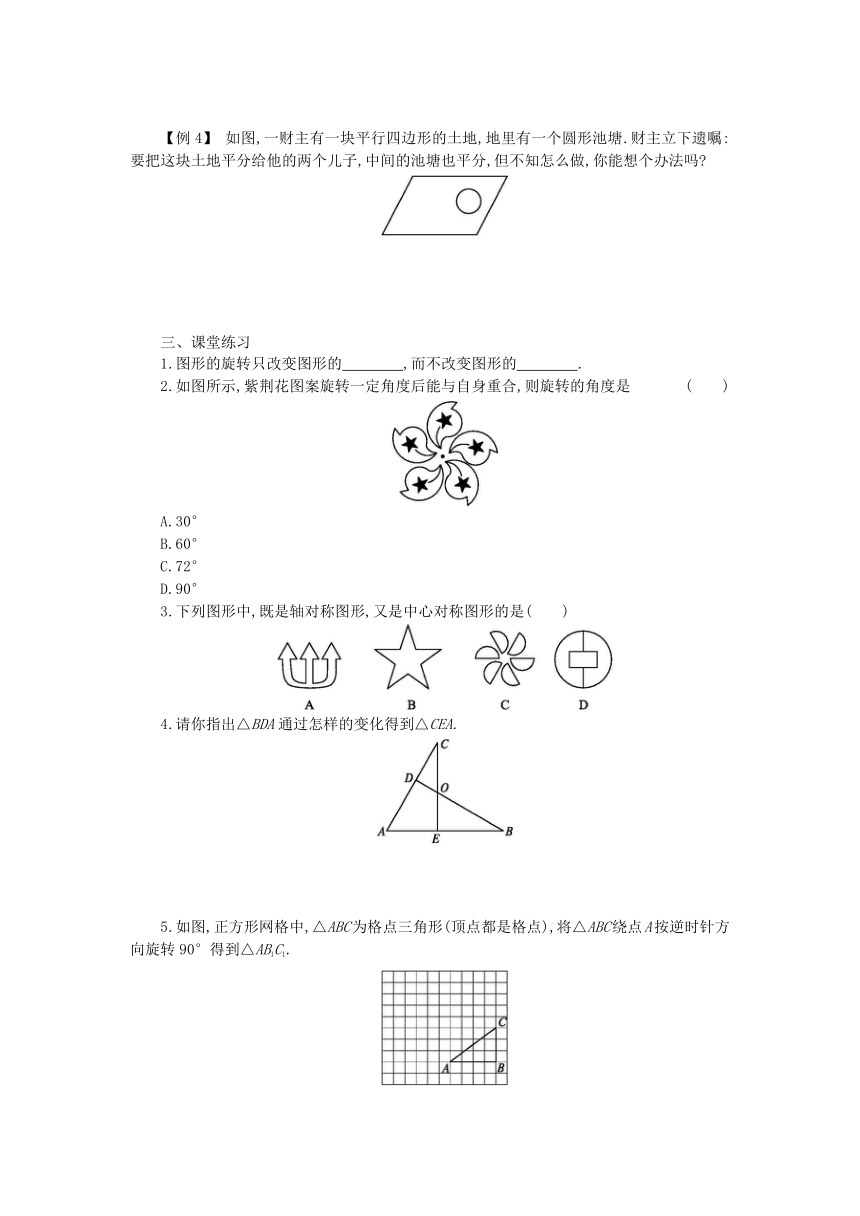
第二十三章 旋转
复习课
学习目标
通过复习系统掌握本章知识.
学习过程
一、自主思考
填空:
1.把一个图形绕着某一点O转动一个角度的图形变换叫做 ,点O叫做 ,转动的角叫做 ,则对应点到旋转中心的距离 .对应点与旋转中心所连线段的夹角等于 .旋转前后的图形 .?
2.把一个图形绕着某一点O旋转 ,如果它能够与另一个图形重合,那么就说这两个图形 ,这个点叫做 ,这两个图形中的对应点叫做 .则对称点所连线段都经过 ,而且被对称中心所 .关于某点中心对称的两个图形是 .?
二、学习新知
【例1】 请选择一个与众不同的图形( )
【例2】 将△ABO绕点O逆时针旋转90°,得到△A'B'O.若点A的坐标为(a,b),则点A'的坐标为 .?
【例3】 如图,平面上有一正方形ABCD,其中心(即对角线的交点)为O,∠EOF的一边OE交AB于点E,另一边OF交BC于点F,且∠EOF=90°.
(1)当∠EOF绕点O旋转时,∠EOF与正方形的边围成的图形的面积会发生变化吗?
(2)请你猜想:将正方形换成正六边形后,∠EOF的度数为多少时,∠EOF与正六边形的边围成的图形的面积,在∠EOF绕其中心O旋转时也是不变的?如果换成正八边形呢?从中你得到了什么启发?
【例4】 如图,一财主有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间的池塘也平分,但不知怎么做,你能想个办法吗?
三、课堂练习
1.图形的旋转只改变图形的 ,而不改变图形的 .?
2.如图所示,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度是 ( )
A.30°
B.60°
C.72°
D.90°
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.请你指出△BDA通过怎样的变化得到△CEA.
5.如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
(1)在正方形网格中,作出△AB1C1;(不要求写作法)
(2)设网格小正方形的边长为1 cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π)
四、自我检测
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
2.跟我学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪?即∠ABC的度数为( )
A.126° B.108° C.90° D.72°
3.下列图案中,既是轴对称图形又是中心对称图形的是 ( )
4.广告设计人员进行图案设计时,经常将一个基本图案进行轴对称、平移和 等.?
5.以等腰直角△ABC的斜边AB所在的直线为对称轴,作这个△ABC的对称图形△ABC',则所得到的四边形ACBC'一定是 .?
6.如图,在一个10×10的正方形DEFG网格中有一个△ABC.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1.
(2)在网格中画出△ABC绕C点逆时针方向旋转90°得到的△A2B2C.
(3)若以EF所在的直线为x轴,ED所在的直线为y轴建立直角坐标系,写出A1,A2两点的坐标.
7.如图,在△ABC中,A(-2,3),B(-3,1),C(-1,2).
(1)将△ABC向右平移4个单位,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(4)在△A1B1C1,△A2B2C2,△A3B3C3中,哪些是成轴对称的,对称轴是什么?哪些是成中心对称的,对称中心的坐标是什么?
布置作业
1.必做题:课本第76页复习题23第1,2,3题.
2.选做题:课本第76页复习题23第4,5题.
参考答案
一、自主思考
1.旋转 旋转中心 旋转角 相等 旋转角 全等
2.180° 关于这个点对称或中心对称 对称中心 对称点 对称中心 平分 全等图形
二、学习新知
【例1】 D
【例2】 (-b,a)
【例3】 解:连接OA和OB,可证明△AOE≌△BOF,因而得到不管∠EOF怎样变化,阴影部分的面积总等于正方形面积的四分之一,同理可以证明将正方形变成正六边形、正八边形、正n边形都是不变的.
【例4】 解:连接平行四边形的两条对角线,其交点O就是平行四边形的中心,找出圆的圆心O',过O,O'作一条直线l,这条直线l就将地与池塘的面积平分了.
三、课堂练习
1.位置 形状和大小
2.C
3.D 解析:图A,B均是轴对称图形,但不是中心对称图形;图C是中心对称图形,但不是轴对称图形.只有图D既是轴对称图形又是中心对称图形.
4.解:△BDA先绕点A逆时针旋转,使DA和AB在一条直线上,然后再以过A点垂直AB的直线为对称轴作它的对称图形.(或将△BDA绕点A顺时针旋转∠CAB,再以AE为对称轴翻折.)
5.解:(1)作图如下:
(2)线段BC所扫过的图形如图阴影部分所示.
根据网格图知:AB=4,BC=3,所以AC=5,线段BC所扫过的图形的面积S=π(AC2-AB2)=(cm2).
四、自我检测
1.B 解析:图A是轴对称图形,但不是中心对称图形;图C、D均是中心对称图形,但不是轴对称图形.只有图B既是轴对称图形又是中心对称图形.
2.A
3.C 解析:图A只是轴对称图形;图B、D只是中心对称图形,只有图C既是轴对称图形又是中心对称图形.
4.旋转
5.正方形
6.解:如图.A1(8,2), A2(4,9).
7.解:图略.(4)△A2B2C2与△A3B3C3成轴对称,对称轴是y轴;△A3B3C3与△A1B1C1成中心对称,对称中心的坐标是(2,0).
复习课
学习目标
通过复习系统掌握本章知识.
学习过程
一、自主思考
填空:
1.把一个图形绕着某一点O转动一个角度的图形变换叫做 ,点O叫做 ,转动的角叫做 ,则对应点到旋转中心的距离 .对应点与旋转中心所连线段的夹角等于 .旋转前后的图形 .?
2.把一个图形绕着某一点O旋转 ,如果它能够与另一个图形重合,那么就说这两个图形 ,这个点叫做 ,这两个图形中的对应点叫做 .则对称点所连线段都经过 ,而且被对称中心所 .关于某点中心对称的两个图形是 .?
二、学习新知
【例1】 请选择一个与众不同的图形( )
【例2】 将△ABO绕点O逆时针旋转90°,得到△A'B'O.若点A的坐标为(a,b),则点A'的坐标为 .?
【例3】 如图,平面上有一正方形ABCD,其中心(即对角线的交点)为O,∠EOF的一边OE交AB于点E,另一边OF交BC于点F,且∠EOF=90°.
(1)当∠EOF绕点O旋转时,∠EOF与正方形的边围成的图形的面积会发生变化吗?
(2)请你猜想:将正方形换成正六边形后,∠EOF的度数为多少时,∠EOF与正六边形的边围成的图形的面积,在∠EOF绕其中心O旋转时也是不变的?如果换成正八边形呢?从中你得到了什么启发?
【例4】 如图,一财主有一块平行四边形的土地,地里有一个圆形池塘.财主立下遗嘱:要把这块土地平分给他的两个儿子,中间的池塘也平分,但不知怎么做,你能想个办法吗?
三、课堂练习
1.图形的旋转只改变图形的 ,而不改变图形的 .?
2.如图所示,紫荆花图案旋转一定角度后能与自身重合,则旋转的角度是 ( )
A.30°
B.60°
C.72°
D.90°
3.下列图形中,既是轴对称图形,又是中心对称图形的是( )
4.请你指出△BDA通过怎样的变化得到△CEA.
5.如图,正方形网格中,△ABC为格点三角形(顶点都是格点),将△ABC绕点A按逆时针方向旋转90°得到△AB1C1.
(1)在正方形网格中,作出△AB1C1;(不要求写作法)
(2)设网格小正方形的边长为1 cm,用阴影表示出旋转过程中线段BC所扫过的图形,然后求出它的面积.(结果保留π)
四、自我检测
1.下列图形中,既是轴对称图形,又是中心对称图形的是( )
2.跟我学剪五角星:如图,先将一张长方形纸片按图①的虚线对折,得到图②,然后将图②沿虚线折叠得到图③,再将图③沿虚线BC剪下△ABC,展开即可得到一个五角星.若想得到一个正五角星(如图④,正五角星的5个角都是36°),则在图③中应沿什么角度剪?即∠ABC的度数为( )
A.126° B.108° C.90° D.72°
3.下列图案中,既是轴对称图形又是中心对称图形的是 ( )
4.广告设计人员进行图案设计时,经常将一个基本图案进行轴对称、平移和 等.?
5.以等腰直角△ABC的斜边AB所在的直线为对称轴,作这个△ABC的对称图形△ABC',则所得到的四边形ACBC'一定是 .?
6.如图,在一个10×10的正方形DEFG网格中有一个△ABC.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1.
(2)在网格中画出△ABC绕C点逆时针方向旋转90°得到的△A2B2C.
(3)若以EF所在的直线为x轴,ED所在的直线为y轴建立直角坐标系,写出A1,A2两点的坐标.
7.如图,在△ABC中,A(-2,3),B(-3,1),C(-1,2).
(1)将△ABC向右平移4个单位,画出平移后的△A1B1C1;
(2)画出△ABC关于x轴对称的△A2B2C2;
(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;
(4)在△A1B1C1,△A2B2C2,△A3B3C3中,哪些是成轴对称的,对称轴是什么?哪些是成中心对称的,对称中心的坐标是什么?
布置作业
1.必做题:课本第76页复习题23第1,2,3题.
2.选做题:课本第76页复习题23第4,5题.
参考答案
一、自主思考
1.旋转 旋转中心 旋转角 相等 旋转角 全等
2.180° 关于这个点对称或中心对称 对称中心 对称点 对称中心 平分 全等图形
二、学习新知
【例1】 D
【例2】 (-b,a)
【例3】 解:连接OA和OB,可证明△AOE≌△BOF,因而得到不管∠EOF怎样变化,阴影部分的面积总等于正方形面积的四分之一,同理可以证明将正方形变成正六边形、正八边形、正n边形都是不变的.
【例4】 解:连接平行四边形的两条对角线,其交点O就是平行四边形的中心,找出圆的圆心O',过O,O'作一条直线l,这条直线l就将地与池塘的面积平分了.
三、课堂练习
1.位置 形状和大小
2.C
3.D 解析:图A,B均是轴对称图形,但不是中心对称图形;图C是中心对称图形,但不是轴对称图形.只有图D既是轴对称图形又是中心对称图形.
4.解:△BDA先绕点A逆时针旋转,使DA和AB在一条直线上,然后再以过A点垂直AB的直线为对称轴作它的对称图形.(或将△BDA绕点A顺时针旋转∠CAB,再以AE为对称轴翻折.)
5.解:(1)作图如下:
(2)线段BC所扫过的图形如图阴影部分所示.
根据网格图知:AB=4,BC=3,所以AC=5,线段BC所扫过的图形的面积S=π(AC2-AB2)=(cm2).
四、自我检测
1.B 解析:图A是轴对称图形,但不是中心对称图形;图C、D均是中心对称图形,但不是轴对称图形.只有图B既是轴对称图形又是中心对称图形.
2.A
3.C 解析:图A只是轴对称图形;图B、D只是中心对称图形,只有图C既是轴对称图形又是中心对称图形.
4.旋转
5.正方形
6.解:如图.A1(8,2), A2(4,9).
7.解:图略.(4)△A2B2C2与△A3B3C3成轴对称,对称轴是y轴;△A3B3C3与△A1B1C1成中心对称,对称中心的坐标是(2,0).
同课章节目录
