人教版九年级数学上册24.2.2直线和圆的位置关系学案(共4课时,附答案)
文档属性
| 名称 | 人教版九年级数学上册24.2.2直线和圆的位置关系学案(共4课时,附答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 465.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 00:00:00 | ||
图片预览



文档简介
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第1课时)
学习目标
1.理解直线与圆的相交、相切、相离三种位置关系.
2.掌握它们的判定方法.
学习过程设计
一、设计问题,创设情境
活动1:
1.点与圆有几种位置关系?
2.怎样判定点和圆的位置关系?
活动2:
你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
二、信息交流,揭示规律
活动3:
(1)直线和圆的公共点个数的变化情况如何?公共点个数最少时有几个?最多时有几个?
(2)通过刚才的研究,你认为直线和圆的位置关系可分为几种类型?
1.判断下列直线和圆的位置关系.
2.判断下列说法正确与否
(1)直线与圆最多有两个公共点.( )
(2)若C为☉O上的一点,则过点C的直线与☉O相切. ( )
(3)若A,B是☉O外两点,则直线AB与☉O相离. ( )
(4)若C为☉O内一点,则过点C的直线与☉O相交. ( )
活动4:议一议
对比点和圆的位置关系的判定方法,是否还有其他的方法来判断直线与圆的位置关系?
三、运用规律,解决问题
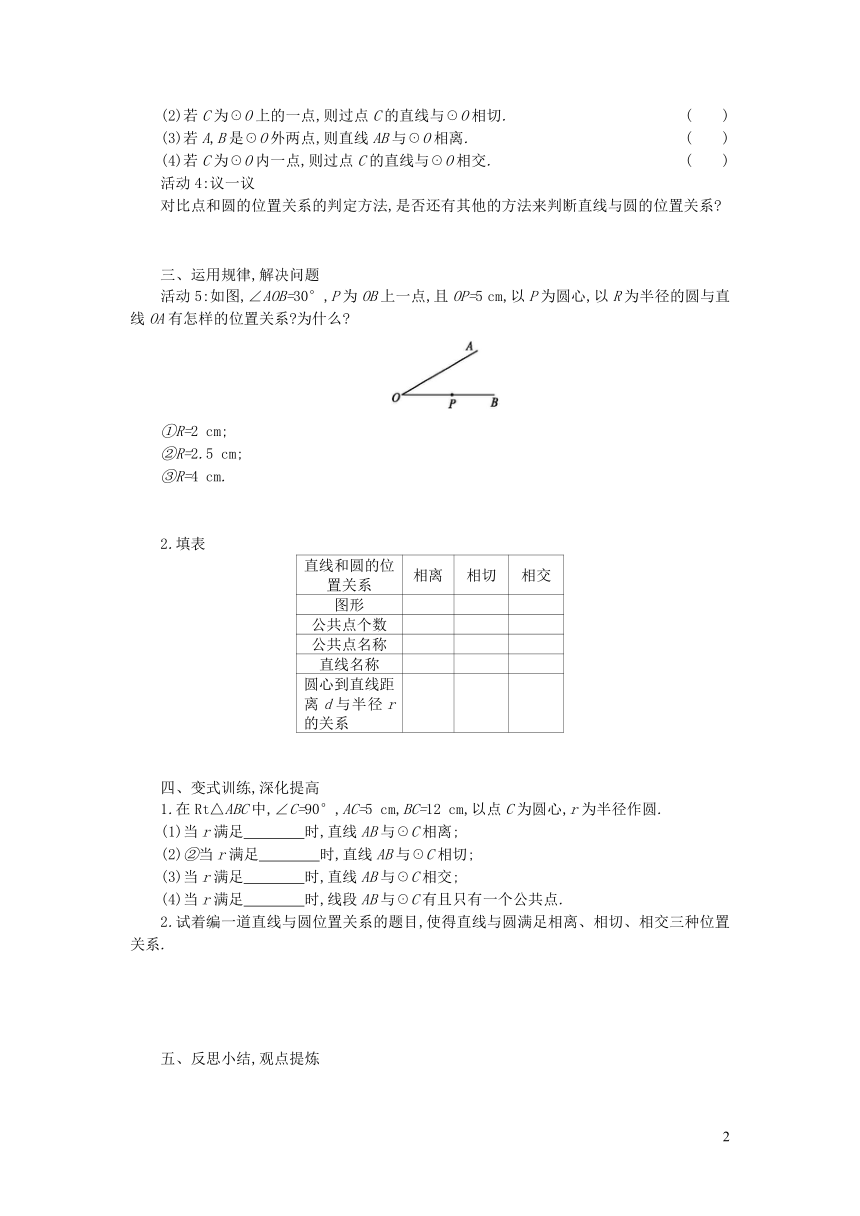
活动5:如图,∠AOB=30°,P为OB上一点,且OP=5 cm,以P为圆心,以R为半径的圆与直线OA有怎样的位置关系?为什么?
①R=2 cm;
②R=2.5 cm;
③R=4 cm.
2.填表
直线和圆的位置关系 相离 相切 相交
图形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
四、变式训练,深化提高
1.在Rt△ABC中,∠C=90°,AC=5 cm,BC=12 cm,以点C为圆心,r为半径作圆.
(1)当r满足 时,直线AB与☉C相离;?
(2)②当r满足 时,直线AB与☉C相切;?
(3)当r满足 时,直线AB与☉C相交;?
(4)当r满足 时,线段AB与☉C有且只有一个公共点.?
2.试着编一道直线与圆位置关系的题目,使得直线与圆满足相离、相切、相交三种位置关系.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
活动1:1.3种
2.(1)点到圆心的距离大于半径时,点在圆外.
(2)点到圆心的距离等于半径时,点在圆上.
(3)点到圆心的距离小于半径时,点在圆内.
活动2:直线和圆有三种位置关系.
二、信息交流,揭示规律
活动3:(1)一开始没有公共点,到有一个公共点,然后有两个公共点;0;2 (2)3种
1.相离;与☉O1相离,与☉O2相交;相切;相交.
2.(1)√ (2)× (3)× (4)√
活动4:利用圆心到直线的距离与半径的大小关系来判断直线与圆的位置关系.
三、运用规律,解决问题
1.解:过点P作PM⊥OA于点M.
在Rt△OMP中,∠AOB=30°,OP=5 cm
∴PM=2.5 cm.
(1)R=2 cm,
∵2<2.5,
∴☉P与OA相离.
(2)R=2.5 cm,
∵2.5=2.5,
∴☉P与OA相切.
(3)R=4 cm,
∵4>2.5,
∴☉P与OA相交.
2.
直线和圆的 位置关系 相离 相切 相交
图形
公共点个数 0 1 2
公共点名称 切点 割点
直线名称 切线 割线
圆心到直线距离d与半径r的关系 d>r d=r d
四、变式训练,深化提高
1.(1)0 (4)r=或52.略
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第2课时)
学习目标
1.掌握切线的判定定理的内容,并会运用它进行切线的证明.
2.能灵活选用切线的三种判定方法判定一条直线是圆的切线.
学习过程设计
一、设计问题,创设情境
1.圆的直径是15 cm,如果直线与圆心的距离分别是(1)5.5 cm,(2)7.5 cm,(3)15 cm,那么直线和圆的位置关系分别是(1) ,(2) ,(3) ;直线和圆的公共点的个数依次是 , , .?
2.你有哪几种方法判断一条直线是圆的切线?
二、信息交流,揭示规律
1.切线的判定定理的得出:
作图:在☉O中,经过半径OA的外端点A作直线l⊥OA,已知OA=r.那么,(1)圆心O到直线l的距离是 ;?
(2)直线l和☉O的位置关系是 .?
归纳:切线的判定定理:
经过 并且 的直线是圆的切线.?
请依据上图,用符号语言表达切线的判定定理:
?
判断:(1)过半径的外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点与半径垂直的直线是圆的切线.( )
2.总结:到此为止学习的切线的判定方法共有:
(1) ;?
(2) ;?
(3) .?
三、运用规律,解决问题
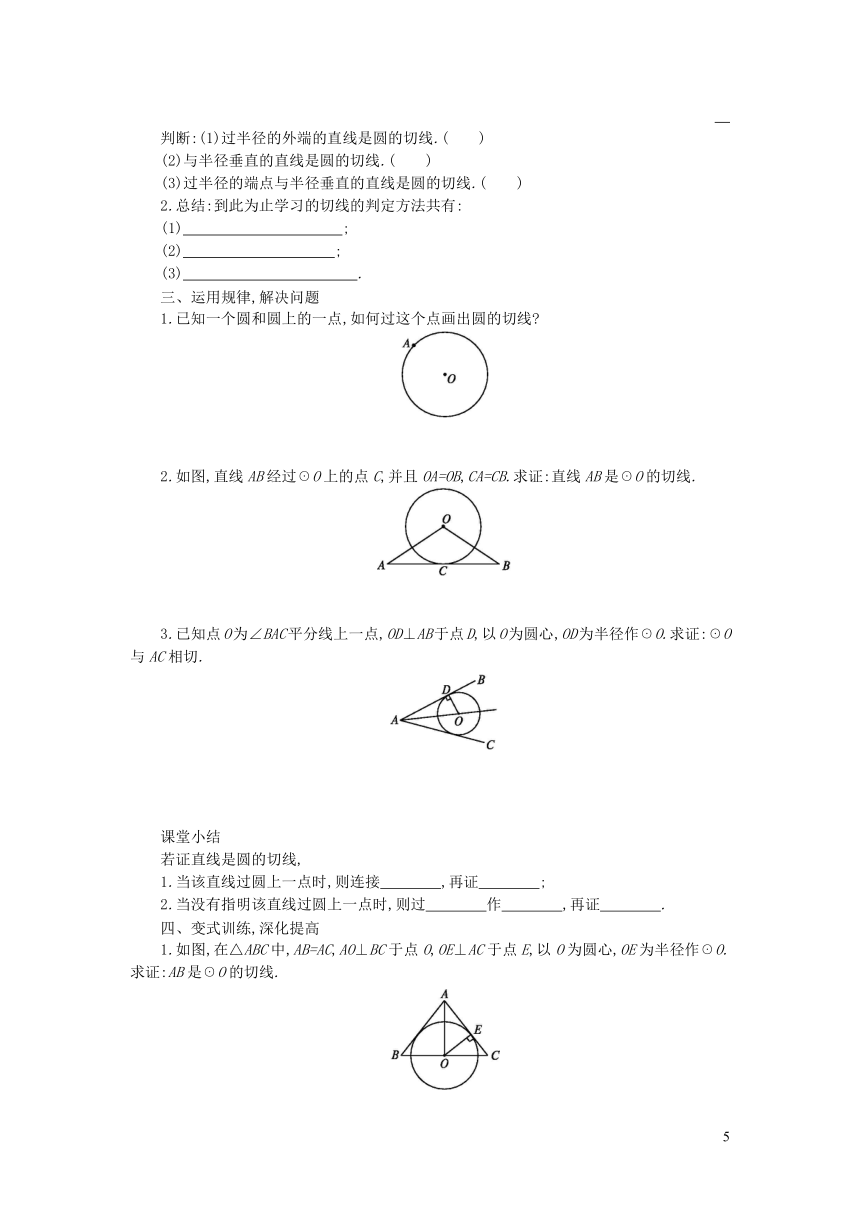
1.已知一个圆和圆上的一点,如何过这个点画出圆的切线?
2.如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:直线AB是☉O的切线.
3.已知点O为∠BAC平分线上一点,OD⊥AB于点D,以O为圆心,OD为半径作☉O.求证:☉O与AC相切.
课堂小结
若证直线是圆的切线,
1.当该直线过圆上一点时,则连接 ,再证 ;?
2.当没有指明该直线过圆上一点时,则过 作 ,再证 .?
四、变式训练,深化提高
1.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AC于点E,以O为圆心,OE为半径作☉O.求证:AB是☉O的切线.
2.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况):① ;② .?
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.相交 相切 相离 2 1 0
2.(1)定义法:和圆有且只有一个公共点的直线是圆的切线.
(2)数量法(d=r):和圆心距离等于半径的直线是圆的切线.
二、信息交流,揭示规律
1.(1)r (2)相切 半径的外端 垂直于半径
∵OA是半径,l⊥OA于点A
∴l是☉O的切线.
判断:(1)× (2)× (3)×
2.总结:(1)定义法:和圆有且只有一个公共点的直线是圆的切线
(2)数量法(d=r):和圆心距离等于半径的直线是圆的切线
(3)判定定理:经过半径外端且垂直于这条半径的直线是圆的切线
三、运用规律,解决问题
1.略
2.证明:连接OC(图略).
∵在△OAB中,OA=OB,CA=CB,
∴AB⊥OC于C.
∵OC是☉O的半径,
∴AB是☉O的切线.
3.证明:过O作OE⊥AC于点E(图略).
∵AO平分∠BAC,OD⊥AB,
∴∠DAO=∠CAO,
∠ADO=∠AEO=90°,
又∵AO=AO,∴△ADO≌△AEO,
∴OE=OD,
即圆心O到AC的距离d=r,
∴AC是☉O的切线.
课堂小结:1.这点和圆心 直线垂直于经过这点的半径
2.圆心 直线的垂线段 这条线段的长等于圆的半径
四、变式训练,深化提高
1.证明:过点O作OF⊥AB于点F
∵AB=AC,AO⊥BC,
∴AO平分∠BAC,
又∵OE⊥AC,OF⊥AB,
∴OE=OF,
∴AB是☉O的切线.
2.(1)AB⊥EF ∠CAE=∠B
(2)证明:过点O作直径AD,连接DC.
∵=,
∴∠D=∠B.
∵AD是直径,
∴∠ACD=90°,
∴∠CAD+∠D=90°,
即∠CAD+∠B=90°.
又∵∠CAE=∠B,
∴∠CAD+∠CAE=90°,
∴OA⊥EF,
∴EF是☉O的切线.
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第3课时)
学习目标
1.理解切线的性质定理内容和推出过程.
2.会用切线的性质定理证明.
学习过程设计
一、设计问题,创设情境
作图1:过☉O外一点P作直线.
作图2:若点A为☉O上的一点,如何过点A作☉O的切线?
二、信息交流,揭示规律
如图,如果直线AB是☉O的切线,切点为点C,那么半径OC与直线AB是不是一定垂直呢?(用反证法说明)
归纳:圆的切线的性质: ?
符号表示:
∵ ?
∴ ?
三、运用规律,解决问题
1.如图,AB是☉O的直径,直线l1,l2是☉O的切线,A,B是切点,l1与l2有怎样的位置关系?证明你的结论.
2.如图,以O为圆心的两个同心圆,大圆的弦AB是小圆的切线,点P为切点,求证:AP=BP.
四、变式训练,深化提高
1.如图,AB为☉O的直径,C为☉O上一点,AD和过C点的切线互相垂直,垂足为点D,求证:AC平分∠DAB.
2.如图,BC切☉O于点B,AB为☉O的直径,弦AD∥OC.求证:CD是☉O的切线.
课堂小结
切线的判定方法:?
切线的性质:?
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
二、信息交流,揭示规律
反证法:假设直线AB与OC不垂直,则过点O作OM⊥l,垂足为点M.
根据垂线段最短,得OM所以直线AB与☉O相交.
这与已知“AB是☉O的切线”矛盾,
所以假设不成立,即AB⊥OC.
归纳:圆的切线垂直于过切点的半径.
AB是☉O的切线
OC⊥AB
三、运用规律,解决问题
1.解:l1∥l2,证明如下:
∵AB是☉O的直径,直线l1,l2是☉O的切线,A、B是切点,
∴AB⊥l1,AB⊥l2,
∴∠1=∠2=90°,∴∠1+∠2=180°,
∴l1∥l2.
2.证明:如图,连接OP.
∵AB是小圆的切线,P为切点,
∴OP⊥AB.
在大圆☉O中,根据垂径定理,得C是AB的中点,
∴AP=BP.
四、变式训练,深化提高
1.证明:连接OC,则OC⊥CD.
∵AD⊥CD,
∴AD∥OC,
∴∠2=∠3.
又∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB.
2.证明:连接OD.
∵BC切☉O于点B.
∴AB⊥CB,
∴∠B=90°.
∵OA=OD,
∴∠A=∠3.
又∵AD∥OC,
∴∠1=∠A,∠2=∠3,
∴∠1=∠2.
∵OD=OB,OC=OC,
∴△OBC≌△ODC,
∴∠B=∠ODC=90°,
∴OD⊥CD,即CD是☉O的切线.
课堂小结:略
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第4课时)
学习目标
1.理解切线长定义.
2.掌握切线长定理并能运用切线长定理解决问题.
3.掌握画三角形内切圆的方法、三角形内心的概念.
学习过程设计
一、设计问题,创设情境
1.已知△ABC,作三个内角的角平分线,说说它们具有什么性质?
2.直线和圆有什么位置关系?切线的判定定理和性质定理的内容是什么?
3.过圆上一点可以作圆的几条切线?过圆外一点呢?圆内一点呢?
二、信息交流,揭示规律
1.如图,经过平面内一点,画出☉O的切线.
切线长定义:? .?
2.如图,点P为☉O外一点,PA,PB为☉O的切线,A,B为切点.连接OP,则线段PA与PB,∠APO与∠BPO分别有什么关系?
由此我们得到切线长定理:? .?
推理形式:
3.如图是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下的圆与三角形的三边都相切?
归纳:与三角形各边 叫做三角形的内切圆,内切圆的圆心是三角形 的交点,叫做三角形的 .?
三、运用规律,解决问题
【例1】 如图,已知☉O是△ABC的内切圆,切点为D、E、F,如果AE=2,CD=1,BF=3,且△ABC的面积为6.求内切圆的半径r.
【例2】 如图,△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13,求AF,BD,CE的长.
四、变式训练,深化提高
探究:PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于点C.
(1)写出图中所有的垂直关系;
(2)写出图中与∠OAC相等的角;
(3)写出图中所有的全等三角形;
(4)写出图中所有的等腰三角形.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.在黑板上作出△ABC的三条角平分线,其性质:①三条角平分线相交于一点;②交点到三条边的距离相等.
2.直线和圆的位置关系同样有三种:直线l和☉O相交?dr.
切线的判定定理:经过半径的外端并且垂直于半径的直线是圆的切线.
切线的性质定理:圆的切线垂直于过切点的半径.
(3)
二、信息交流,揭示规律
1.经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
2.PA=PB,∠APO=∠BPO.
∵PA,PB分别切☉O于点A,B,
∴PA=PB,∠APO=∠BPO.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
3.方法:略
归纳:都相切的圆 三条角平分线 内心
三、运用规律,解决问题
【例1】 解:连接AO,BO,CO.
∵☉O是△ABC的内切圆且D,E,F是切点,
∴AF=AE=2,BD=BF=3,CE=CD=1,
∴AB=5,BC=4,AC=3.
又∵S△ABC=6,
∴(4+5+3)r=6,
∴r=1.
∴所求的内切圆的半径为1.
【例2】 解:设AF=x,则AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由CD+BD=BC可得
(13-x)+(9-x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
四、变式训练,深化提高
探究:(1)OA⊥PA,OB⊥PB,AB⊥OP.
(2)∠OAC=∠OBC=∠APC=∠BPC.
(3)△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP.
(4)△ABP,△AOB.
五、反思小结,观点提炼
略
1
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第1课时)
学习目标
1.理解直线与圆的相交、相切、相离三种位置关系.
2.掌握它们的判定方法.
学习过程设计
一、设计问题,创设情境
活动1:
1.点与圆有几种位置关系?
2.怎样判定点和圆的位置关系?
活动2:
你能根据直线和圆的公共点个数想象一下,直线和圆有几种位置关系吗?
二、信息交流,揭示规律
活动3:
(1)直线和圆的公共点个数的变化情况如何?公共点个数最少时有几个?最多时有几个?
(2)通过刚才的研究,你认为直线和圆的位置关系可分为几种类型?
1.判断下列直线和圆的位置关系.
2.判断下列说法正确与否
(1)直线与圆最多有两个公共点.( )
(2)若C为☉O上的一点,则过点C的直线与☉O相切. ( )
(3)若A,B是☉O外两点,则直线AB与☉O相离. ( )
(4)若C为☉O内一点,则过点C的直线与☉O相交. ( )
活动4:议一议
对比点和圆的位置关系的判定方法,是否还有其他的方法来判断直线与圆的位置关系?
三、运用规律,解决问题
活动5:如图,∠AOB=30°,P为OB上一点,且OP=5 cm,以P为圆心,以R为半径的圆与直线OA有怎样的位置关系?为什么?
①R=2 cm;
②R=2.5 cm;
③R=4 cm.
2.填表
直线和圆的位置关系 相离 相切 相交
图形
公共点个数
公共点名称
直线名称
圆心到直线距离d与半径r的关系
四、变式训练,深化提高
1.在Rt△ABC中,∠C=90°,AC=5 cm,BC=12 cm,以点C为圆心,r为半径作圆.
(1)当r满足 时,直线AB与☉C相离;?
(2)②当r满足 时,直线AB与☉C相切;?
(3)当r满足 时,直线AB与☉C相交;?
(4)当r满足 时,线段AB与☉C有且只有一个公共点.?
2.试着编一道直线与圆位置关系的题目,使得直线与圆满足相离、相切、相交三种位置关系.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
活动1:1.3种
2.(1)点到圆心的距离大于半径时,点在圆外.
(2)点到圆心的距离等于半径时,点在圆上.
(3)点到圆心的距离小于半径时,点在圆内.
活动2:直线和圆有三种位置关系.
二、信息交流,揭示规律
活动3:(1)一开始没有公共点,到有一个公共点,然后有两个公共点;0;2 (2)3种
1.相离;与☉O1相离,与☉O2相交;相切;相交.
2.(1)√ (2)× (3)× (4)√
活动4:利用圆心到直线的距离与半径的大小关系来判断直线与圆的位置关系.
三、运用规律,解决问题
1.解:过点P作PM⊥OA于点M.
在Rt△OMP中,∠AOB=30°,OP=5 cm
∴PM=2.5 cm.
(1)R=2 cm,
∵2<2.5,
∴☉P与OA相离.
(2)R=2.5 cm,
∵2.5=2.5,
∴☉P与OA相切.
(3)R=4 cm,
∵4>2.5,
∴☉P与OA相交.
2.
直线和圆的 位置关系 相离 相切 相交
图形
公共点个数 0 1 2
公共点名称 切点 割点
直线名称 切线 割线
圆心到直线距离d与半径r的关系 d>r d=r d
四、变式训练,深化提高
1.(1)0
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第2课时)
学习目标
1.掌握切线的判定定理的内容,并会运用它进行切线的证明.
2.能灵活选用切线的三种判定方法判定一条直线是圆的切线.
学习过程设计
一、设计问题,创设情境
1.圆的直径是15 cm,如果直线与圆心的距离分别是(1)5.5 cm,(2)7.5 cm,(3)15 cm,那么直线和圆的位置关系分别是(1) ,(2) ,(3) ;直线和圆的公共点的个数依次是 , , .?
2.你有哪几种方法判断一条直线是圆的切线?
二、信息交流,揭示规律
1.切线的判定定理的得出:
作图:在☉O中,经过半径OA的外端点A作直线l⊥OA,已知OA=r.那么,(1)圆心O到直线l的距离是 ;?
(2)直线l和☉O的位置关系是 .?
归纳:切线的判定定理:
经过 并且 的直线是圆的切线.?
请依据上图,用符号语言表达切线的判定定理:
?
判断:(1)过半径的外端的直线是圆的切线.( )
(2)与半径垂直的直线是圆的切线.( )
(3)过半径的端点与半径垂直的直线是圆的切线.( )
2.总结:到此为止学习的切线的判定方法共有:
(1) ;?
(2) ;?
(3) .?
三、运用规律,解决问题
1.已知一个圆和圆上的一点,如何过这个点画出圆的切线?
2.如图,直线AB经过☉O上的点C,并且OA=OB,CA=CB.求证:直线AB是☉O的切线.
3.已知点O为∠BAC平分线上一点,OD⊥AB于点D,以O为圆心,OD为半径作☉O.求证:☉O与AC相切.
课堂小结
若证直线是圆的切线,
1.当该直线过圆上一点时,则连接 ,再证 ;?
2.当没有指明该直线过圆上一点时,则过 作 ,再证 .?
四、变式训练,深化提高
1.如图,在△ABC中,AB=AC,AO⊥BC于点O,OE⊥AC于点E,以O为圆心,OE为半径作☉O.求证:AB是☉O的切线.
2.已知:△ABC内接于☉O,过点A作直线EF.
(1)如图1,AB为直径,要使EF为☉O的切线,还需添加的条件是(只需写出两种情况):① ;② .?
(2)如图2,AB是非直径的弦,∠CAE=∠B,求证:EF是☉O的切线.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.相交 相切 相离 2 1 0
2.(1)定义法:和圆有且只有一个公共点的直线是圆的切线.
(2)数量法(d=r):和圆心距离等于半径的直线是圆的切线.
二、信息交流,揭示规律
1.(1)r (2)相切 半径的外端 垂直于半径
∵OA是半径,l⊥OA于点A
∴l是☉O的切线.
判断:(1)× (2)× (3)×
2.总结:(1)定义法:和圆有且只有一个公共点的直线是圆的切线
(2)数量法(d=r):和圆心距离等于半径的直线是圆的切线
(3)判定定理:经过半径外端且垂直于这条半径的直线是圆的切线
三、运用规律,解决问题
1.略
2.证明:连接OC(图略).
∵在△OAB中,OA=OB,CA=CB,
∴AB⊥OC于C.
∵OC是☉O的半径,
∴AB是☉O的切线.
3.证明:过O作OE⊥AC于点E(图略).
∵AO平分∠BAC,OD⊥AB,
∴∠DAO=∠CAO,
∠ADO=∠AEO=90°,
又∵AO=AO,∴△ADO≌△AEO,
∴OE=OD,
即圆心O到AC的距离d=r,
∴AC是☉O的切线.
课堂小结:1.这点和圆心 直线垂直于经过这点的半径
2.圆心 直线的垂线段 这条线段的长等于圆的半径
四、变式训练,深化提高
1.证明:过点O作OF⊥AB于点F
∵AB=AC,AO⊥BC,
∴AO平分∠BAC,
又∵OE⊥AC,OF⊥AB,
∴OE=OF,
∴AB是☉O的切线.
2.(1)AB⊥EF ∠CAE=∠B
(2)证明:过点O作直径AD,连接DC.
∵=,
∴∠D=∠B.
∵AD是直径,
∴∠ACD=90°,
∴∠CAD+∠D=90°,
即∠CAD+∠B=90°.
又∵∠CAE=∠B,
∴∠CAD+∠CAE=90°,
∴OA⊥EF,
∴EF是☉O的切线.
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第3课时)
学习目标
1.理解切线的性质定理内容和推出过程.
2.会用切线的性质定理证明.
学习过程设计
一、设计问题,创设情境
作图1:过☉O外一点P作直线.
作图2:若点A为☉O上的一点,如何过点A作☉O的切线?
二、信息交流,揭示规律
如图,如果直线AB是☉O的切线,切点为点C,那么半径OC与直线AB是不是一定垂直呢?(用反证法说明)
归纳:圆的切线的性质: ?
符号表示:
∵ ?
∴ ?
三、运用规律,解决问题
1.如图,AB是☉O的直径,直线l1,l2是☉O的切线,A,B是切点,l1与l2有怎样的位置关系?证明你的结论.
2.如图,以O为圆心的两个同心圆,大圆的弦AB是小圆的切线,点P为切点,求证:AP=BP.
四、变式训练,深化提高
1.如图,AB为☉O的直径,C为☉O上一点,AD和过C点的切线互相垂直,垂足为点D,求证:AC平分∠DAB.
2.如图,BC切☉O于点B,AB为☉O的直径,弦AD∥OC.求证:CD是☉O的切线.
课堂小结
切线的判定方法:?
切线的性质:?
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
二、信息交流,揭示规律
反证法:假设直线AB与OC不垂直,则过点O作OM⊥l,垂足为点M.
根据垂线段最短,得OM
这与已知“AB是☉O的切线”矛盾,
所以假设不成立,即AB⊥OC.
归纳:圆的切线垂直于过切点的半径.
AB是☉O的切线
OC⊥AB
三、运用规律,解决问题
1.解:l1∥l2,证明如下:
∵AB是☉O的直径,直线l1,l2是☉O的切线,A、B是切点,
∴AB⊥l1,AB⊥l2,
∴∠1=∠2=90°,∴∠1+∠2=180°,
∴l1∥l2.
2.证明:如图,连接OP.
∵AB是小圆的切线,P为切点,
∴OP⊥AB.
在大圆☉O中,根据垂径定理,得C是AB的中点,
∴AP=BP.
四、变式训练,深化提高
1.证明:连接OC,则OC⊥CD.
∵AD⊥CD,
∴AD∥OC,
∴∠2=∠3.
又∵OA=OC,
∴∠1=∠3,
∴∠1=∠2,
即AC平分∠DAB.
2.证明:连接OD.
∵BC切☉O于点B.
∴AB⊥CB,
∴∠B=90°.
∵OA=OD,
∴∠A=∠3.
又∵AD∥OC,
∴∠1=∠A,∠2=∠3,
∴∠1=∠2.
∵OD=OB,OC=OC,
∴△OBC≌△ODC,
∴∠B=∠ODC=90°,
∴OD⊥CD,即CD是☉O的切线.
课堂小结:略
五、反思小结,观点提炼
略
第二十四章 圆
24.2 点和圆、直线和圆的位置关系
24.2.2 直线和圆的位置关系(第4课时)
学习目标
1.理解切线长定义.
2.掌握切线长定理并能运用切线长定理解决问题.
3.掌握画三角形内切圆的方法、三角形内心的概念.
学习过程设计
一、设计问题,创设情境
1.已知△ABC,作三个内角的角平分线,说说它们具有什么性质?
2.直线和圆有什么位置关系?切线的判定定理和性质定理的内容是什么?
3.过圆上一点可以作圆的几条切线?过圆外一点呢?圆内一点呢?
二、信息交流,揭示规律
1.如图,经过平面内一点,画出☉O的切线.
切线长定义:? .?
2.如图,点P为☉O外一点,PA,PB为☉O的切线,A,B为切点.连接OP,则线段PA与PB,∠APO与∠BPO分别有什么关系?
由此我们得到切线长定理:? .?
推理形式:
3.如图是一张三角形的铁皮,如何在它上面截下一块圆形的用料,并且使截下的圆与三角形的三边都相切?
归纳:与三角形各边 叫做三角形的内切圆,内切圆的圆心是三角形 的交点,叫做三角形的 .?
三、运用规律,解决问题
【例1】 如图,已知☉O是△ABC的内切圆,切点为D、E、F,如果AE=2,CD=1,BF=3,且△ABC的面积为6.求内切圆的半径r.
【例2】 如图,△ABC的内切圆☉O与BC,CA,AB分别相切于点D,E,F,且AB=9,BC=14,CA=13,求AF,BD,CE的长.
四、变式训练,深化提高
探究:PA,PB是☉O的两条切线,A,B为切点,直线OP交☉O于点D,E,交AB于点C.
(1)写出图中所有的垂直关系;
(2)写出图中与∠OAC相等的角;
(3)写出图中所有的全等三角形;
(4)写出图中所有的等腰三角形.
五、反思小结,观点提炼
参考答案
一、设计问题,创设情境
1.在黑板上作出△ABC的三条角平分线,其性质:①三条角平分线相交于一点;②交点到三条边的距离相等.
2.直线和圆的位置关系同样有三种:直线l和☉O相交?d
切线的判定定理:经过半径的外端并且垂直于半径的直线是圆的切线.
切线的性质定理:圆的切线垂直于过切点的半径.
(3)
二、信息交流,揭示规律
1.经过圆外一点作圆的切线,这点和切点之间的线段长,叫做这点到圆的切线长.
2.PA=PB,∠APO=∠BPO.
∵PA,PB分别切☉O于点A,B,
∴PA=PB,∠APO=∠BPO.
从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角.
3.方法:略
归纳:都相切的圆 三条角平分线 内心
三、运用规律,解决问题
【例1】 解:连接AO,BO,CO.
∵☉O是△ABC的内切圆且D,E,F是切点,
∴AF=AE=2,BD=BF=3,CE=CD=1,
∴AB=5,BC=4,AC=3.
又∵S△ABC=6,
∴(4+5+3)r=6,
∴r=1.
∴所求的内切圆的半径为1.
【例2】 解:设AF=x,则AE=x,
CD=CE=AC-AE=13-x,
BD=BF=AB-AF=9-x,
由CD+BD=BC可得
(13-x)+(9-x)=14.
解得x=4.
因此AF=4,BD=5,CE=9.
四、变式训练,深化提高
探究:(1)OA⊥PA,OB⊥PB,AB⊥OP.
(2)∠OAC=∠OBC=∠APC=∠BPC.
(3)△AOP≌△BOP,△AOC≌△BOC,△ACP≌△BCP.
(4)△ABP,△AOB.
五、反思小结,观点提炼
略
1
同课章节目录
