沪科版八年级数学上册第13章 三角形中的边角关系、命题与证明单元测试卷2含解析
文档属性
| 名称 | 沪科版八年级数学上册第13章 三角形中的边角关系、命题与证明单元测试卷2含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 166.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 16:30:49 | ||
图片预览




文档简介
绝密★启用前
三角形中的边角关系单元测试卷
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题4分,共20分)
1.在△ABC中,∠A=30°,∠B=75°,则△ABC是( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.等腰三角形
2.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14 B.10 C.3 D.2
3.有下列三个命题:
(1)两点之间线段最短
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)过直线外一点有且只有一条直线与这条直线平行
其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
4.在△ABC中,AD是中线,AB=12 cm,AC=10 cm,则△ABD和△ACD的周长差为( )
A.7 cm B.6 cm C.2 cm D.14 cm
5.等腰△ABC的周长为20,其中一边长为9,则这个等腰三角形的腰长为( )
A.5.5 B.9 C.11 D.5.5或9
6.如图,将纸片沿折叠,使点落在四边形外点的位置,则下列结论正确的是( )
A. B.
C. D.
7.已知△ABC中,∠A与∠C的度数比为5:7,且∠B比∠A大10°,那么∠B为(? )
A.40° B.50° C.60° D.70°
8.三角形三条高的交点在一边上,则这个三角形是? (????? )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
9.如图,若∠1>∠2,则∠1,∠2,∠3用“<”号连接,正确的是( )
A.∠3<∠2<∠1 B.∠2<∠3<∠1 C.∠2<∠1<∠3 D.以上都不对
10.如图,∠MAN=100°,点B,C是射线AM,AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为( )
A.40° B.50° C.80° D.随点B,C的移动而变化
第II卷(非选择题)
二、填空题(每题5分,共20分)
11.写出命题“内错角相等”的逆命题_____.
12.一副分别含30°和45°角的两个直角三角板拼成如图所示的图形,其中∠C=90°,∠B=45°,∠E=30°.则∠AFE=______________.
13.如图, 已知AD、DE、EF分别是△ABC,△ABD,△AED的中线,若S△ABc=24cm2,则阴影部分△DEF的面积为____________cm2.
14.如图,在△ABC中,∠B=50°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______°.
三、解答题
15.已知三角形的三边长分别是x,x?1,x+1.求x的取值范围。
16.如图,在△DBC中,BD⊥CD,BA平分∠DBC,∠BAC=124°,求∠C的度数.
17.如图所示,已知P是△ABC内一点,试说明PA+PB+PC>(AB+BC+AC).
18.如图,已知AB∥CD,若∠A=20°,∠E=35°,求∠C的度数.
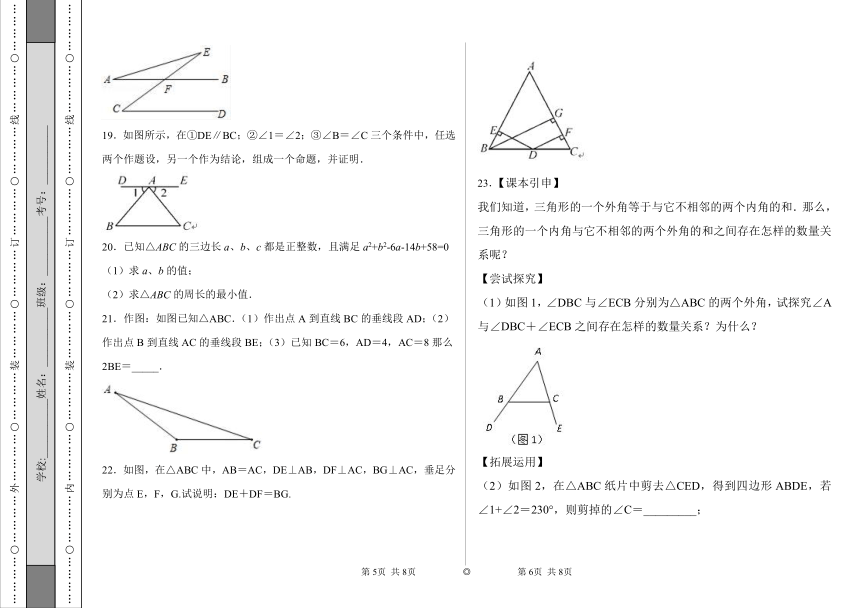
19.如图所示,在①DE∥BC;②∠1=∠2;③∠B=∠C三个条件中,任选两个作题设,另一个作为结论,组成一个命题,并证明.
20.已知△ABC的三边长a、b、c都是正整数,且满足a2+b2-6a-14b+58=0
(1)求a、b的值;
(2)求△ABC的周长的最小值.
21.作图:如图已知△ABC.(1)作出点A到直线BC的垂线段AD;(2)作出点B到直线AC的垂线段BE;(3)已知BC=6,AD=4,AC=8那么2BE=_____.
22.如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为点E,F,G.试说明:DE+DF=BG.
23.【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.D
【解析】试题解析:∵在△ABC中,∠A=30°,∠B=75°,
∴∠C=180°-30°-75°=75°,
∴△ABC是等腰三角形.
故选D.
2.B
【解析】
【详解】
设第三边是x,由三角形边的性质可得:8-5 ∴3所以选B.
3.D
【解析】
试题分析:利用线段公理、垂线的性质等知识分别判断后即可确定正确的选项.
解:(1)两点之间线段最短,正确,是真命题;
(2)平面内,过一点能且只能作一条直线与已知直线垂直,正确,是真命题;
(3)过直线外一点有且只有一条直线与这条直线平行,正确,是真命题,
故选D.
4.C
【解析】
分析:由三角形中线的定义推知BD=DC;然后根据三角形的周长的定义知△ABD与△ADC的周长之差为(AB-AC).
详解:∵如图,在△ABC中,AD是△ABC的中线,
∴BD=CD.
∵△ABD的周长=AB+AD+BD,△ADC的周长=AC+AD+CD=AC+AD+BD,
∴△ABD与△ADC的周长之差为:AB-AC=12-10=2.
故选C.
点睛:本题考查了三角形的中线的定义,三角形周长的计算.解题时,根据三角形的周长的计算方法得到:△ABD的周长和△ADC的周长的差就是AB与AC的差是解答本题的关键.
5.D
【解析】
(1)设长为9的边为腰,则底边为:20-9-9=2,因为9、9、2能围成三角形,所以这个等腰三角形的腰长可以为9;
(2)设长为9的边为底边,则腰长为: ,因为9、5.5、5.5能围成三角形,所以这个等腰三角形的腰长可以为5.5.
综上所述,这个等腰三角形的腰长为9或5.5.
故选D.
点睛:(1)解这类题时,一般都需分已知边是腰或底两种情况讨论;(2)求出的结果必须用三角形三边间的关系检验,看能否围成三角形.
6.D
【解析】
【分析】
根据折叠的性质和三角形的外角的性质解答即可.
【详解】
解:如图:
∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
∵∠1=∠A+∠3,∠3=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠1-∠2=2∠A,
故选:D.
【点睛】
本题考查的是三角形的外角性质和图形的翻折变换,理清图中角与角的关系是解决问题的关键.
7.C
【解析】
依题意可设∠A与∠C的度数分别为5n°、7n°,则∠B=∠A+10°=5n°+10°,
在△ABC中,∠A+∠B+∠C=180°,即5n°+5n°+10°+7n°=180°,解得n°=10°.
所以∠B=60°.故选C.
8.B
【解析】
锐角三角形的三条高线交于三角形内部,钝角三角形的三条高线交于三角形外部,直角三角形的高线交于三角形的直角顶点。故选B
9.C
【解析】
分析:由三角形外角的性质知, ∠3>∠1, ∠3>∠2,结合已知条件∠1>∠2,可求出结论.
详解:∵∠3>∠1, ∠3>∠2, ∠1>∠2,
∴∠2<∠1<∠3.
故选C.
点睛:本题考查了三角形外角的性质:三角形的外角大于任何一个与它不相邻的内角,熟练掌握这一性质是解答本题的关键..
10.B
【解析】
试题解析:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故选B.
11.如果两个角相等,那么这两个角是内错角
【解析】
将原命题的条件与结论互换就得到其逆命题,故其逆命题为:如果两个角相等,那么这两个角是内错角.
故答案是:如果两个角相等,那么这两个角是内错角.
12.15°
【解析】
∵∠C=90°,∠B=45°,
∴∠BAC=45°,
又∵∠BAC=∠E+∠AFE,∠E=30°,
∴∠AFE=45°-30°=15°.
13.3
【解析】
∵三角形一边上的中线把三角形分成面积相等的两个三角形,且AD、DE、EF分别是△ABC、△ABD、△AED的中线,
∴S△ABD=S△ABC,S△ADE=S△ABD,S△DEF=S△ADE,
∵S△ABC=24cm2,
∴S△DEF=3cm2.
14.65
【解析】
如图,∵AE平分∠DAC,CE平分∠ACF,
∴∠1=∠DAC,∠2=∠ACF,
∴∠1+∠2=(∠DAC+∠ACF),
又∵∠DAC+∠ACF=(180°-∠BAC)+(180°-∠ACB)=360°-(∠BAC+∠ACB),且
∠BAC+∠ACB=180°-∠ABC=180°-50°=130°,
∴∠1+∠2=(360°-130°)=115°,
∴在△ACE中,∠E=180°-(∠1+∠2)=180°-115°=65°.
15.x>2.
【解析】
【分析】
根据三角形的三边关系列出关于x的不等式组,求出x的取值范围即可;
【详解】
∵三角形的三边长分别是x,x?1,x+1,
∴x+1?(x?1)解得:x>2,
∴x的取值范围是x>2.
【点睛】
此题考查三角形三边关系,解一元一次不等式组,解题关键在于列出不等式.
16.∠C=22°.
【解析】
分析:首先根据三角形的一个外角等于和它不相邻的两个内角的和求得∠DBA的度数,再根据角平分线的概念求得∠DBC的度数,最后根据三角形的内角和定理即可求解.
详解:在△ABD中,∠BAC=∠D+∠DBA.
∵BD⊥CD,∴∠D=90°.
又∵∠BAC=124°
,∴∠DBA =34°.
∵BA平分∠DBC,
∴∠DBC=2∠DBA=68°,
∠C=180°-(∠D+∠DBC)=22°.
点睛:本题考查了三角形外角的性质,角平分线的定义,三角形内角和定理,根据外角的性质求出∠DBA =34°是解答本题的关键.
17.见解析
【解析】
【分析】
根据三角形三边的关系定理:三角形的任意两边之和大于三角形的第三边,任意两边之差小于三角形第三边证明即可.
【详解】
在△APB中,AP+BP>AB,
同理BP+PC>BC,PC+AP>AC,
三式相加得2(AP+BP+PC)>AB+AC+BC,
∴AP+BP+CP>(AB+AC+BC).
【点睛】
此题考查三角形三边关系定理,解题关键在于掌握三角形三边的关系.
18.55°.
【解析】
试题分析:根据三角形的外角等于和它不相邻的两个内角的和以及平行线的性质进行求解.
试题解析:∵∠A=20°,∠E=35°,
∴∠EFB=∠A+∠E=55°,
∵AB∥CD,
∴∠C=∠EFB=55°.
考点:1.三角形的外角性质;2.平行线的性质.
19.见解析.
【解析】
分析:依据题意,一共能组成2个命题,它们是:题设:DE//BC,∠1=∠2,结论:∠B=∠C;题设:DE//BC,∠B=∠C,结论:∠1=∠2;可根据“同位角相等,两直线平行”,“两直线平行,同位角相等”来写出证明过程即可.
详解:已知,DE∥BC,∠1=∠2.
求证:∠B=∠C.
证明:∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠1=∠2,
∴∠B=∠C.
点睛:本题考查了平行线的判定与性质.应用平行线的判定和性质定理时,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系;故要求一定要弄清题设和结论,切莫混淆.
20.(1)a=3,b=7;(2)△ABC周长的最小值为15.
【解析】
【分析】
(1)根据完全平方公式整理成非负数的和的形式,再根据非负数的性质列式求出a、b;
(2)根据三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出第三边的取值范围,再求出第三边最小时的值,再求解即可.
【详解】
解:(1)∵a2+b2-6a-14b+58=(a2-6a+9)+(b2-14b+49)=(a-3)2+(b-7)2=0,
∴a-3=0,b-7=0,
解得a=3,b=7;
(2)∵a、b、c是△ABC的三边长,
∴b-a<c<a+b,
即4<c<10,
要使△ABC周长的最小只需使得边长c最小,
又∵c是正整数,
∴c的最小值是5,
∴△ABC周长的最小值为3+5+7=15.
故答案为:(1)a=3,b=7;(2)△ABC周长的最小值为15.
【点睛】
本题考查因式分解的实际运用,掌握完全平方公式,利用完全平方式的特点分解是解决问题的关键.也考查了三角形三边关系.
21.(1)见解析;(2)见解析;(3)6
【解析】
【分析】
(1)根据尺规作垂线的方法作图即可;
(2)根据尺规作垂线的方法作图即可;
(3)利用三角形的面积求出BE即得结果.
【详解】
解:(1)线段AD如图所示.
(2)线段BE如图所示.
(3)∵S△ABC=?BC?AD=?AC?BE,
∴BE=,
∴2BE=6.
故答案为6.
【点睛】
本题考查了基本的尺规作图和利用三角形的面积求高的知识,熟练尺规作垂线的方法和步骤是作图的关键.
22.说明见解析.
【解析】
试题分析:连结AD.根据△ABC的面积=△ABD的面积+△ACD的面积,以及AB=AC,即可得到DE+DF=BG.
试题解析:证明:连结AD.
则△ABC的面积=△ABD的面积+△ACD的面积,
AB?DE+AC?DF=AC?BG,
∵AB=AC,
∴DE+DF=BG.
23.(1)∠DBC+∠ECB =180°+∠A (2)50°(3)∠P=90°-∠A (4)∠BAD+∠CDA=360°-2∠P.
【解析】试题分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;
(2)根据(1)的结论整理计算即可得解;
(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;
(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解;
试题解析:
(1)∠DBC+∠ECB=180°-∠ABC+180°-∠ACB
=360°-(∠ABC+∠ACB)
=360°-(180°-∠A)
=180°+∠A
(2)50°
(3)∠P=90°-∠A
(4)延长BA、CD交于点Q,
则∠P=90°-∠Q,∴∠Q=180°-2∠P.
∴∠BAD+∠CDA=180°+∠Q=180°+180°-2∠P=360°-2∠P.
点睛:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键。
答案第1页,总2页
答案第1页,总2页
三角形中的边角关系单元测试卷
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题4分,共20分)
1.在△ABC中,∠A=30°,∠B=75°,则△ABC是( )
A.直角三角形 B.钝角三角形 C.等边三角形 D.等腰三角形
2.若一个三角形的两边长分别为5和8,则第三边长可能是( )
A.14 B.10 C.3 D.2
3.有下列三个命题:
(1)两点之间线段最短
(2)平面内,过一点能且只能作一条直线与已知直线垂直
(3)过直线外一点有且只有一条直线与这条直线平行
其中真命题的个数是( )
A.0个 B.1个 C.2个 D.3个
4.在△ABC中,AD是中线,AB=12 cm,AC=10 cm,则△ABD和△ACD的周长差为( )
A.7 cm B.6 cm C.2 cm D.14 cm
5.等腰△ABC的周长为20,其中一边长为9,则这个等腰三角形的腰长为( )
A.5.5 B.9 C.11 D.5.5或9
6.如图,将纸片沿折叠,使点落在四边形外点的位置,则下列结论正确的是( )
A. B.
C. D.
7.已知△ABC中,∠A与∠C的度数比为5:7,且∠B比∠A大10°,那么∠B为(? )
A.40° B.50° C.60° D.70°
8.三角形三条高的交点在一边上,则这个三角形是? (????? )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.以上都有可能
9.如图,若∠1>∠2,则∠1,∠2,∠3用“<”号连接,正确的是( )
A.∠3<∠2<∠1 B.∠2<∠3<∠1 C.∠2<∠1<∠3 D.以上都不对
10.如图,∠MAN=100°,点B,C是射线AM,AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为( )
A.40° B.50° C.80° D.随点B,C的移动而变化
第II卷(非选择题)
二、填空题(每题5分,共20分)
11.写出命题“内错角相等”的逆命题_____.
12.一副分别含30°和45°角的两个直角三角板拼成如图所示的图形,其中∠C=90°,∠B=45°,∠E=30°.则∠AFE=______________.
13.如图, 已知AD、DE、EF分别是△ABC,△ABD,△AED的中线,若S△ABc=24cm2,则阴影部分△DEF的面积为____________cm2.
14.如图,在△ABC中,∠B=50°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_______°.
三、解答题
15.已知三角形的三边长分别是x,x?1,x+1.求x的取值范围。
16.如图,在△DBC中,BD⊥CD,BA平分∠DBC,∠BAC=124°,求∠C的度数.
17.如图所示,已知P是△ABC内一点,试说明PA+PB+PC>(AB+BC+AC).
18.如图,已知AB∥CD,若∠A=20°,∠E=35°,求∠C的度数.
19.如图所示,在①DE∥BC;②∠1=∠2;③∠B=∠C三个条件中,任选两个作题设,另一个作为结论,组成一个命题,并证明.
20.已知△ABC的三边长a、b、c都是正整数,且满足a2+b2-6a-14b+58=0
(1)求a、b的值;
(2)求△ABC的周长的最小值.
21.作图:如图已知△ABC.(1)作出点A到直线BC的垂线段AD;(2)作出点B到直线AC的垂线段BE;(3)已知BC=6,AD=4,AC=8那么2BE=_____.
22.如图,在△ABC中,AB=AC,DE⊥AB,DF⊥AC,BG⊥AC,垂足分别为点E,F,G.试说明:DE+DF=BG.
23.【课本引申】
我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在怎样的数量关系呢?
【尝试探究】
(1)如图1,∠DBC与∠ECB分别为△ABC的两个外角,试探究∠A与∠DBC+∠ECB之间存在怎样的数量关系?为什么?
【拓展运用】
(2)如图2,在△ABC纸片中剪去△CED,得到四边形ABDE,若∠1+∠2=230°,则剪掉的∠C=_________;
(3)小明联想到了曾经解决的一个问题:如图3,在△ABC中,BP、CP分别平分外角∠DBC、∠ECB,∠P与∠A有何数量关系?请直接写出答案_ .
(4)如图4,在四边形ABCD中,BP、CP分别平分外角∠EBC、∠FCB,∠P与∠A、∠D有何数量关系?为什么?(若需要利用上面的结论说明,可直接使用,不需说明理由)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.D
【解析】试题解析:∵在△ABC中,∠A=30°,∠B=75°,
∴∠C=180°-30°-75°=75°,
∴△ABC是等腰三角形.
故选D.
2.B
【解析】
【详解】
设第三边是x,由三角形边的性质可得:8-5
3.D
【解析】
试题分析:利用线段公理、垂线的性质等知识分别判断后即可确定正确的选项.
解:(1)两点之间线段最短,正确,是真命题;
(2)平面内,过一点能且只能作一条直线与已知直线垂直,正确,是真命题;
(3)过直线外一点有且只有一条直线与这条直线平行,正确,是真命题,
故选D.
4.C
【解析】
分析:由三角形中线的定义推知BD=DC;然后根据三角形的周长的定义知△ABD与△ADC的周长之差为(AB-AC).
详解:∵如图,在△ABC中,AD是△ABC的中线,
∴BD=CD.
∵△ABD的周长=AB+AD+BD,△ADC的周长=AC+AD+CD=AC+AD+BD,
∴△ABD与△ADC的周长之差为:AB-AC=12-10=2.
故选C.
点睛:本题考查了三角形的中线的定义,三角形周长的计算.解题时,根据三角形的周长的计算方法得到:△ABD的周长和△ADC的周长的差就是AB与AC的差是解答本题的关键.
5.D
【解析】
(1)设长为9的边为腰,则底边为:20-9-9=2,因为9、9、2能围成三角形,所以这个等腰三角形的腰长可以为9;
(2)设长为9的边为底边,则腰长为: ,因为9、5.5、5.5能围成三角形,所以这个等腰三角形的腰长可以为5.5.
综上所述,这个等腰三角形的腰长为9或5.5.
故选D.
点睛:(1)解这类题时,一般都需分已知边是腰或底两种情况讨论;(2)求出的结果必须用三角形三边间的关系检验,看能否围成三角形.
6.D
【解析】
【分析】
根据折叠的性质和三角形的外角的性质解答即可.
【详解】
解:如图:
∵△A′DE是△ADE沿DE折叠得到,
∴∠A′=∠A,
∵∠1=∠A+∠3,∠3=∠A′+∠2,
∴∠1=∠A+∠A′+∠2,
∴∠1-∠2=2∠A,
故选:D.
【点睛】
本题考查的是三角形的外角性质和图形的翻折变换,理清图中角与角的关系是解决问题的关键.
7.C
【解析】
依题意可设∠A与∠C的度数分别为5n°、7n°,则∠B=∠A+10°=5n°+10°,
在△ABC中,∠A+∠B+∠C=180°,即5n°+5n°+10°+7n°=180°,解得n°=10°.
所以∠B=60°.故选C.
8.B
【解析】
锐角三角形的三条高线交于三角形内部,钝角三角形的三条高线交于三角形外部,直角三角形的高线交于三角形的直角顶点。故选B
9.C
【解析】
分析:由三角形外角的性质知, ∠3>∠1, ∠3>∠2,结合已知条件∠1>∠2,可求出结论.
详解:∵∠3>∠1, ∠3>∠2, ∠1>∠2,
∴∠2<∠1<∠3.
故选C.
点睛:本题考查了三角形外角的性质:三角形的外角大于任何一个与它不相邻的内角,熟练掌握这一性质是解答本题的关键..
10.B
【解析】
试题解析:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故选B.
11.如果两个角相等,那么这两个角是内错角
【解析】
将原命题的条件与结论互换就得到其逆命题,故其逆命题为:如果两个角相等,那么这两个角是内错角.
故答案是:如果两个角相等,那么这两个角是内错角.
12.15°
【解析】
∵∠C=90°,∠B=45°,
∴∠BAC=45°,
又∵∠BAC=∠E+∠AFE,∠E=30°,
∴∠AFE=45°-30°=15°.
13.3
【解析】
∵三角形一边上的中线把三角形分成面积相等的两个三角形,且AD、DE、EF分别是△ABC、△ABD、△AED的中线,
∴S△ABD=S△ABC,S△ADE=S△ABD,S△DEF=S△ADE,
∵S△ABC=24cm2,
∴S△DEF=3cm2.
14.65
【解析】
如图,∵AE平分∠DAC,CE平分∠ACF,
∴∠1=∠DAC,∠2=∠ACF,
∴∠1+∠2=(∠DAC+∠ACF),
又∵∠DAC+∠ACF=(180°-∠BAC)+(180°-∠ACB)=360°-(∠BAC+∠ACB),且
∠BAC+∠ACB=180°-∠ABC=180°-50°=130°,
∴∠1+∠2=(360°-130°)=115°,
∴在△ACE中,∠E=180°-(∠1+∠2)=180°-115°=65°.
15.x>2.
【解析】
【分析】
根据三角形的三边关系列出关于x的不等式组,求出x的取值范围即可;
【详解】
∵三角形的三边长分别是x,x?1,x+1,
∴x+1?(x?1)
∴x的取值范围是x>2.
【点睛】
此题考查三角形三边关系,解一元一次不等式组,解题关键在于列出不等式.
16.∠C=22°.
【解析】
分析:首先根据三角形的一个外角等于和它不相邻的两个内角的和求得∠DBA的度数,再根据角平分线的概念求得∠DBC的度数,最后根据三角形的内角和定理即可求解.
详解:在△ABD中,∠BAC=∠D+∠DBA.
∵BD⊥CD,∴∠D=90°.
又∵∠BAC=124°
,∴∠DBA =34°.
∵BA平分∠DBC,
∴∠DBC=2∠DBA=68°,
∠C=180°-(∠D+∠DBC)=22°.
点睛:本题考查了三角形外角的性质,角平分线的定义,三角形内角和定理,根据外角的性质求出∠DBA =34°是解答本题的关键.
17.见解析
【解析】
【分析】
根据三角形三边的关系定理:三角形的任意两边之和大于三角形的第三边,任意两边之差小于三角形第三边证明即可.
【详解】
在△APB中,AP+BP>AB,
同理BP+PC>BC,PC+AP>AC,
三式相加得2(AP+BP+PC)>AB+AC+BC,
∴AP+BP+CP>(AB+AC+BC).
【点睛】
此题考查三角形三边关系定理,解题关键在于掌握三角形三边的关系.
18.55°.
【解析】
试题分析:根据三角形的外角等于和它不相邻的两个内角的和以及平行线的性质进行求解.
试题解析:∵∠A=20°,∠E=35°,
∴∠EFB=∠A+∠E=55°,
∵AB∥CD,
∴∠C=∠EFB=55°.
考点:1.三角形的外角性质;2.平行线的性质.
19.见解析.
【解析】
分析:依据题意,一共能组成2个命题,它们是:题设:DE//BC,∠1=∠2,结论:∠B=∠C;题设:DE//BC,∠B=∠C,结论:∠1=∠2;可根据“同位角相等,两直线平行”,“两直线平行,同位角相等”来写出证明过程即可.
详解:已知,DE∥BC,∠1=∠2.
求证:∠B=∠C.
证明:∵DE∥BC,
∴∠1=∠B,∠2=∠C.
又∵∠1=∠2,
∴∠B=∠C.
点睛:本题考查了平行线的判定与性质.应用平行线的判定和性质定理时,平行线的判定是由角的数量关系判断两直线的位置关系,平行线的性质是由平行关系来寻找角的数量关系;故要求一定要弄清题设和结论,切莫混淆.
20.(1)a=3,b=7;(2)△ABC周长的最小值为15.
【解析】
【分析】
(1)根据完全平方公式整理成非负数的和的形式,再根据非负数的性质列式求出a、b;
(2)根据三角形的任意两边之和大于第三边,三角形的任意两边之差小于第三边求出第三边的取值范围,再求出第三边最小时的值,再求解即可.
【详解】
解:(1)∵a2+b2-6a-14b+58=(a2-6a+9)+(b2-14b+49)=(a-3)2+(b-7)2=0,
∴a-3=0,b-7=0,
解得a=3,b=7;
(2)∵a、b、c是△ABC的三边长,
∴b-a<c<a+b,
即4<c<10,
要使△ABC周长的最小只需使得边长c最小,
又∵c是正整数,
∴c的最小值是5,
∴△ABC周长的最小值为3+5+7=15.
故答案为:(1)a=3,b=7;(2)△ABC周长的最小值为15.
【点睛】
本题考查因式分解的实际运用,掌握完全平方公式,利用完全平方式的特点分解是解决问题的关键.也考查了三角形三边关系.
21.(1)见解析;(2)见解析;(3)6
【解析】
【分析】
(1)根据尺规作垂线的方法作图即可;
(2)根据尺规作垂线的方法作图即可;
(3)利用三角形的面积求出BE即得结果.
【详解】
解:(1)线段AD如图所示.
(2)线段BE如图所示.
(3)∵S△ABC=?BC?AD=?AC?BE,
∴BE=,
∴2BE=6.
故答案为6.
【点睛】
本题考查了基本的尺规作图和利用三角形的面积求高的知识,熟练尺规作垂线的方法和步骤是作图的关键.
22.说明见解析.
【解析】
试题分析:连结AD.根据△ABC的面积=△ABD的面积+△ACD的面积,以及AB=AC,即可得到DE+DF=BG.
试题解析:证明:连结AD.
则△ABC的面积=△ABD的面积+△ACD的面积,
AB?DE+AC?DF=AC?BG,
∵AB=AC,
∴DE+DF=BG.
23.(1)∠DBC+∠ECB =180°+∠A (2)50°(3)∠P=90°-∠A (4)∠BAD+∠CDA=360°-2∠P.
【解析】试题分析:(1)根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠DBC+∠ECB,再利用三角形内角和定理整理即可得解;
(2)根据(1)的结论整理计算即可得解;
(3)表示出∠DBC+∠ECB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形内角和定理列式整理即可得解;
(4)延长BA、CD相交于点Q,先用∠Q表示出∠P,再用(1)的结论整理即可得解;
试题解析:
(1)∠DBC+∠ECB=180°-∠ABC+180°-∠ACB
=360°-(∠ABC+∠ACB)
=360°-(180°-∠A)
=180°+∠A
(2)50°
(3)∠P=90°-∠A
(4)延长BA、CD交于点Q,
则∠P=90°-∠Q,∴∠Q=180°-2∠P.
∴∠BAD+∠CDA=180°+∠Q=180°+180°-2∠P=360°-2∠P.
点睛:本题考查了三角形的一个外角等于与它不相邻的两个内角的和的性质,三角形的内角和定理,角平分线的定义,熟记性质并读懂题目信息是解题的关键。
答案第1页,总2页
答案第1页,总2页
