沪科版八年级数学上册第13章 三角形中的边角关系、命题与证明单元测试卷3含解析
文档属性
| 名称 | 沪科版八年级数学上册第13章 三角形中的边角关系、命题与证明单元测试卷3含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 368.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 16:48:10 | ||
图片预览

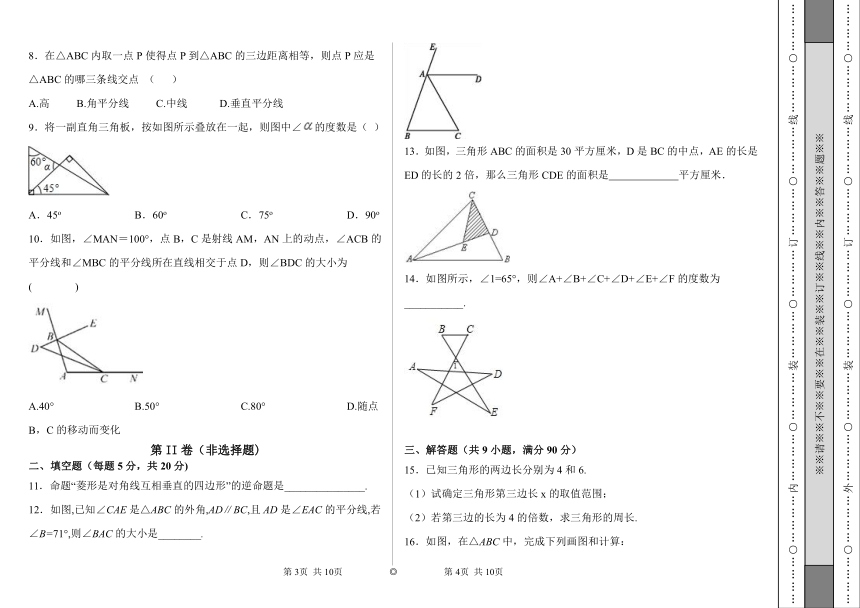

文档简介
绝密★启用前
三角形中的边角关系单元测试卷
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题4分,共20分)
1.适合条件∠A=∠B=∠C的三角形ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
2.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7 C.-3<x<11 D.x>3
3.下列命题中,属于假命题的是( )
A.等腰三角形两底角相等 B.内错角相等,两直线平行
C.矩形的对角线相等 D.相等的角是对顶角
4.如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A.1个 B.2个 C.3个 D.4个
5.已知等腰△ABC的两条边长分别是5和6,则△ABC的周长为( )
A.11 B.16 C.17 D.16或17
6.如图所示,∠1=∠2=150°,则∠3=( )
A.30° B.150° C.120° D.60°
7.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
8.在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )
A.高 B.角平分线 C.中线 D.垂直平分线
9.将一副直角三角板,按如图所示叠放在一起,则图中∠的度数是( )
A.45o B.60o C.75o D.90o
10.如图,∠MAN=100°,点B,C是射线AM,AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为( )
A.40° B.50° C.80° D.随点B,C的移动而变化
第II卷(非选择题)
二、填空题(每题5分,共20分)
11.命题“菱形是对角线互相垂直的四边形”的逆命题是_______________.
12.如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线,若∠B=71°,则∠BAC的大小是________.
13.如图,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是 平方厘米.
14.如图所示,∠1=65°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.
三、解答题(共9小题,满分90分)
15.已知三角形的两边长分别为4和6.
(1)试确定三角形第三边长x的取值范围;
(2)若第三边的长为4的倍数,求三角形的周长.
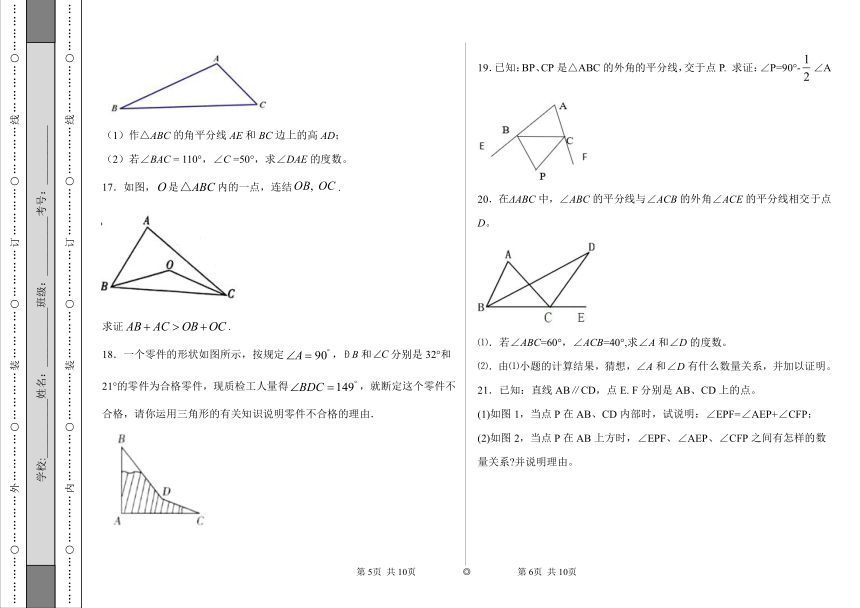
16.如图,在△ABC中,完成下列画图和计算:
(1)作△ABC的角平分线AE和BC边上的高AD;
(2)若∠BAC = 110°,∠C =50°,求∠DAE的度数。
17.如图,是内的一点,连结.
求证.
18.一个零件的形状如图所示,按规定,和分别是32°和21°的零件为合格零件,现质检工人量得,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
19.已知:BP、CP是△ABC的外角的平分线,交于点P. 求证:∠P=90°-∠A
20.在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。
⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
21.已知:直线AB∥CD,点E. F分别是AB、CD上的点。
(1)如图1,当点P在AB、CD内部时,试说明:∠EPF=∠AEP+∠CFP;
(2)如图2,当点P在AB上方时,∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。
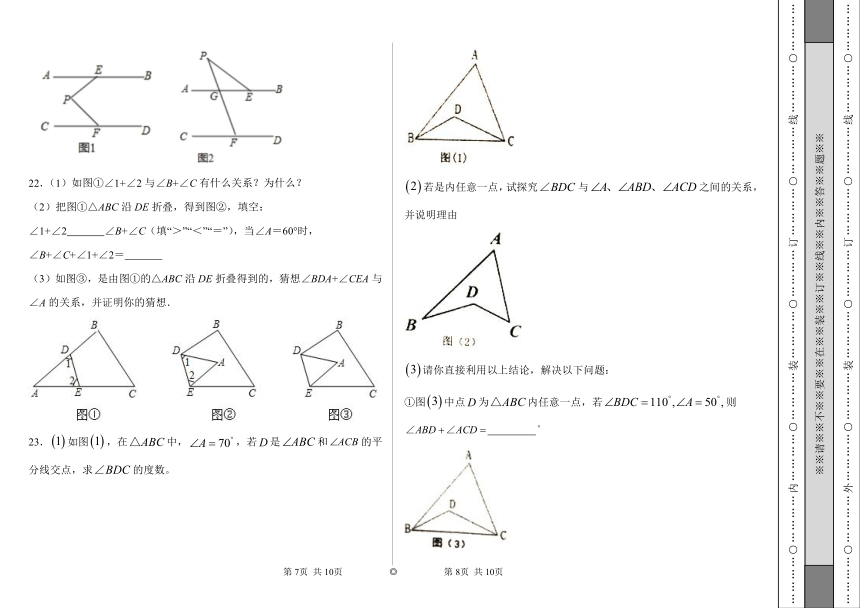
22.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:
∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=60°时,∠B+∠C+∠1+∠2=
(3)如图③,是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并证明你的猜想.
23.如图,在中,,若是和的平分线交点,求的度数。
若是内任意一点,试探究与之间的关系,并说明理由
请你直接利用以上结论,解决以下问题:
①图中点为内任意一点,若则
②如图平分平分,若,求的度数.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.B
【解析】
试题解析:∵∠A=∠B=∠C,
∴设∠A=x,则∠B=2x,∠C=3x,
∵三角形的内角和是180°,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
2.A
【解析】∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11,
故选A.
3.D
【解析】对于D相等的角可以是对顶角,也可以是同位角,所以D错误。所以选D。
4.B
【解析】
解:①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;
②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;
③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;
④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.
故选B.
点睛:本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.
5.D
【解析】
分5是腰长与底边长两种情况讨论:①5是腰长时,三边分别为5、5、6时,能组成三角形,周长=5+5+6=16;②5是底边时,三边分别为5、6、6,能组成三角形,周长=5+6+6=17.
综上所述,等腰三角形的周长为16或17.故选D.
6.D
【解析】
【分析】
由∠1,∠2的度数,利用邻补角互补可求出∠ABC,∠BAC的度数,再利用三角形的外角性质即可求出∠3的度数.
【详解】
解:∵∠1=∠2=150°,
∴∠ABC=∠BAC=180°-150°=30°,
∴∠3=∠ABC+∠BAC=60°.
故选:D.
【点睛】
本题考查了三角形的外角性质以及邻补角,牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键.
7.C
【解析】
【分析】
利用三角形内角和定理求解即可.
【详解】
因为三角形内角和为180°,且∠A = 60°,∠B = 75°,所以∠C=180°–60°–75°=45°.
【点睛】
三角形内角和定理是常考的知识点.
8.B
【解析】解:∵到三角形三边距离相等的点是三角形三条角平分线的交点,
∴点P应是△ABC的三条角平分线的交点.
故选B.
9.C
【解析】
如图,
∵∠1=90°-60°=30°,
∴∠α=45°+30°=75°。故选C。
10.B
【解析】
试题解析:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故选B.
11.对角线互相垂直的四边形是菱形
【解析】分析:把一个命题的条件和结论互换就得到它的逆命题.
详解:命题“菱形是对角线互相垂直的四边形”的逆命题是“对角线互相垂直的四边形是菱形”.
点睛:本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
12.38°
【解析】
试题分析:由AD∥BC可得∠EAD=∠B=71°,由AD是的平分线可得∠EAC=2∠EAD=2×71°=142°,则∠BAC=180°–=180°–142°=38°.
考点:三角形的外角性质;平行线的性质.
13.5
【解析】
解:S△ABD=S△ADC=S△ABC=×30=15(平方厘米);
S△CAE:S△CDE=2:1,
S△CDE=S△ADC=×15=5(平方厘米);
答:三角形CDE的面积是5平方厘米.
14.230°
【解析】
【分析】
依据三角形内角和定理,即可得到∠B+∠C=115°,∠MGH+∠MHG=115°,再根据三角形外角性质,即可得出∠A+∠B+∠C+∠D+∠E+∠F的度数.
【详解】
如图所示,
∵∠1=∠BMC=65°,
∴∠B+∠C=180°?65°=115°,∠MGH+∠MHG=115°,
又∵∠MGH是△DFG的外角,∠MHG是△AEH的外角,
∴∠MGH=∠F+∠D,∠MHG=∠A+∠E,
∴∠F+∠D+∠A+∠E=∠MGH+∠MHG=115°,
∴∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°,
故答案为:230°.
【点睛】
本题考查了三角形的外角和三角形的内角和的相关知识,解决本题的关键是利用三角形外角性质:三角形的一个外角等于和它不相邻的两个内角的和.
15.(1) 2【解析】分析:(1),根据“三角形中,任意两边之和大于第三边,两边之差小于第三边”即可得到第三边x的取值范围;(2) 根据(1)中第三边的取值范围,再结合等腰三角形的性质,即可得到第三边的长,最后根据三角形周长公式进行计算即可.
本题解析:
(1)由三角形三边关系,得x>6-4且x<6+4,即x>2且x<10.所以2(2)由(1)可知,x的值为4或8,所以三角形周长为14或18.
16.(1)见解析;(2)15°
【解析】
【分析】
(1)根据角平分线及垂线的画法作图即可;
(2)利用角平分线把一个角平分的性质和高线得到90°的性质可得∠DAE的度数.
【详解】
(1)如图,
(2)解:∵ AE平分∠BAC,∠BAC=110°,
∴∠CAC=∠BAC=55° ,
∵ AD是BC边上的高,
∴∠ADC=90° ,
∵∠C=50°,
∴∠CAD=180°- ∠C- ∠ADC=40°,
∴∠EAD=∠CAE- ∠CAD=15°.
【点睛】
本题考查了三角形的高与角平分线的画法;求三角形同一顶点处的高线与角平分线的夹角注意运用角平分线的性质,高线的性质,以及三角形内角和定理.
17.见解析
【解析】
【分析】
延长BP交AC于点D,在△ABD中可得OB+OD<AB+AD,在△OCD中,OC<OD+CD然后把两个不等式相加整理后可得结论.
【详解】
证明:延长BO交AC于点D,
在△ABD中,OB+OD<AB+AD①,
在△OCD中,OC<OD+CD②,
①+②得OB+OD+OC<AB+AD+OD+CD,
即OB+OC<AB+AC,
即:.
【点睛】
此题考查三角形的三边关系,关键是熟练掌握三角形的三边关系定理:两边之和大于第三边.
18.零件不合格,理由详见解析
【解析】
【分析】
按题意作出四边形ABDC,再想办法利用三角形关于角的性质验证,验证的关键在于找出∠BDC与∠A、∠B、∠C之间的关系.
【详解】
连接AD,并延长至点E.
由于∠CDE=∠CAD+∠C,∠BDE=∠BAD+∠B,
所以∠CDE+∠BDE=∠CAD+∠C+∠BAD+∠B,
即∠CDB=∠BAC+∠B+∠C.
如果零件合格,那么∠CDB=90°+32°+21°=143°,
而现量得∠BDC=149°.
故零件不合格.
【点睛】
此题考查三角形内角和定理,三角形的外角性质,解题关键在于掌握各性质定义和作辅助线.
19.见解析.
【解析】
【分析】
利用角平分线的性质和三角形外角的性质得到∠PBC=(∠A+∠ACB),∠PCB=(∠A+∠ABC),然后根据三角形内角和定理得出结论.
【详解】
证明:∵BP、CP分别是△ABC两个外角∠EBC和∠BCF的平分线,
∴∠PBC=∠EBC=(∠A+∠ACB),∠PCB=∠BCF=(∠A+∠ABC),
∴∠P=180°?∠PBC?∠PCB=180°?(∠A+∠ACB+∠A+∠ABC),
∵∠A+∠ACB+∠BAC=180°,
∴∠P=180°?(∠A+180°)=90°?∠A.
【点睛】
此题主要考查了三角形外角的性质、三角形内角和定理以及角平分线的性质,正确应用角平分线的性质是解题关键.
20.(1)∠A=80°,∠D=40°;(2)∠A=2∠D,理由见解析
【解析】
【分析】
(1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
【详解】
(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°?∠ABC?∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=∠ABC=×60°=30°,
∠ACD= (180°?∠ACB)=×140°=70°,
∴∠D=180°?∠DBC?∠ACB?∠ACD=180°?30°?40°?70°=40°,
∴∠A=80°,∠D=40°;
(2)通过第(1)的计算,得到∠A=2∠D,理由如下:
∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE?∠DBC),∠D=∠DCE?∠DBC,
∴∠A=2∠D.
【点睛】
此题考查三角形内角和定理,三角形的外角性质,解题关键在于根据角平分线定义和外角的性质即可求得∠D度数.
21.(1)见解析;(2)∠AEP+∠EPF=∠CFP,理由见解析;
【解析】
【详解】
(1) 证明:过P点作PG∥AB,如图1,
∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠CFP,
∴∠AEP+∠CFP=∠EPF;
(2)∠AEP+∠EPF=∠CFP,理由如下:
∵∠AEP+∠EPF=∠AGP,
∵CD∥AB,
∴∠APG=∠CFP,
∴∠AEP+∠EPF=∠CFP.
【点睛】
此题考查三角形外角的性质以及平行线的性质,解题关键在于作辅助线和利用平行线的性质得到得到∠EPG=∠AEP.
22.(1)∠1+∠2=∠B+∠C;理由见解析;
(2)=;240°
(3)∠BDA+∠CEA=2∠A;理由见解析.
【解析】
【分析】
(1)根据三角形的内角和定理即可推得∠1+∠2与∠B+∠C的关系;
(2)由折叠的性质和(1)的结论可得∠1+∠2与∠B+∠C的关系;当∠A=60°时,先求出∠B+∠C的度数,再利用前者的结论即可得出答案;
(3)如图③,延长BD交CE的延长线于A′,利用三角形的外角的性质即可得出结论:∠BDA+∠CEA=2∠A.
【详解】
解:(1)根据三角形内角是180°,可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;
(2)由折叠的性质知:图②的∠1+∠2就是图①的∠1+∠2,而由(1)知:∠1+∠2=∠B+∠C;
∴在图②中有∠1+∠2=∠B+∠C;
当∠A=60°时,∠B+∠C=180°﹣∠A=120°,
∴∠B+∠C+∠1+∠2=120°×2=240°;
故答案为:=;240°
(3)∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
理由如下:如图③,延长BD交CE的延长线于A′,连接AA′.
∵∠BDA=∠DA′A+∠DAA′,∠AEC=∠EA′A+∠EAA′,∠DA′E=∠DAE,
∴∠BDA+∠AEC=2∠DAE,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
【点睛】
本题考查了折叠的性质、三角形的内角和定理与三角形外角的性质,熟练掌握三角形的内角和定理和三角形外角的性质是解此题的关键.
23.(1)∠BDC=125°;(2)∠BDC=∠BAC+∠ABD+∠ACD,理由见解析;(3)①60;②∠DCE=90°.
【解析】
【分析】
(1)根据三角形的内角和与DB平分∠ABC,DC平分∠ACB可求得∠DBC+∠DCB的度数,再在△DBC中应用三角形内角和定理即可求出结果;
(2)作射线AD,再运用三角形的外角性质即可得出结论;
(3)①直接应用(2)的结论计算即可;
②先由(2)的结论求出∠ADB+∠AEB的度数,再由CD平分∠ADB,CE平分∠ACB可求出∠ADC+∠AEC的度数,然后再运用(2)的结论即可求出结果.
【详解】
解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵DB平分∠ABC,DC平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×110°=55°,
∴∠BDC=180°-55°=125°;
(2)∠BDC=∠BAC+∠ABD+∠ACD,理由如下:
如图2,作射线AD,∵∠1、∠2分别是△ABD和△ACD的外角,
∴∠1=∠BAD+∠ABD,∠2=∠CAD+∠ACD,
∴∠BDC=∠1+∠2=∠BAD+∠ABD+∠CAD+∠ACD=∠BAC+∠ABD+∠ACD.
(3)①由(2)的结论可得:∠ABD+∠ACD=∠BDC―∠A=110°-50°=60°;故答案为60;
②由(2)的结论可得:∠ADB+∠AEB=∠DBE―∠A=130°-50°=80°;
∵CD平分∠ADB,CE平分∠ACB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC=(∠ADB+∠AEB)=×80°=40°,
又∵∠DCE=∠ADC+∠A+∠AEC,
∴∠DCE=50°+40°=90°.
【点睛】
本题考查了角平分线的定义、三角形的内角和定理、三角形的外角定理和整体代入求解的数学思想,熟练掌握三角形的内角和定理和外角性质、灵活应用整体代入的数学思想是解题的关键.
答案第1页,总2页
答案第1页,总2页
三角形中的边角关系单元测试卷
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.请将答案正确填写在答题卡上
第I卷(选择题)
一、单选题(每题4分,共20分)
1.适合条件∠A=∠B=∠C的三角形ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.都有可能
2.一个三角形的三边长分别为4,7,x,那么x的取值范围是( )
A.3<x<11 B.4<x<7 C.-3<x<11 D.x>3
3.下列命题中,属于假命题的是( )
A.等腰三角形两底角相等 B.内错角相等,两直线平行
C.矩形的对角线相等 D.相等的角是对顶角
4.如图,在△ABC中,∠1=∠2,G为AD的中点,BG的延长线交AC于点E,F为AB上的一点,CF与AD垂直,交AD于点H,则下面判断正确的有( )
①AD是△ABE的角平分线;②BE是△ABD的边AD上的中线;
③CH是△ACD的边AD上的高;④AH是△ACF的角平分线和高
A.1个 B.2个 C.3个 D.4个
5.已知等腰△ABC的两条边长分别是5和6,则△ABC的周长为( )
A.11 B.16 C.17 D.16或17
6.如图所示,∠1=∠2=150°,则∠3=( )
A.30° B.150° C.120° D.60°
7.一个缺角的三角形ABC残片如图所示,量得∠A=60°,∠B=75°,则这个三角形残缺前的∠C的度数为( )
A.75° B.60° C.45° D.40°
8.在△ABC内取一点P使得点P到△ABC的三边距离相等,则点P应是△ABC的哪三条线交点 ( )
A.高 B.角平分线 C.中线 D.垂直平分线
9.将一副直角三角板,按如图所示叠放在一起,则图中∠的度数是( )
A.45o B.60o C.75o D.90o
10.如图,∠MAN=100°,点B,C是射线AM,AN上的动点,∠ACB的平分线和∠MBC的平分线所在直线相交于点D,则∠BDC的大小为( )
A.40° B.50° C.80° D.随点B,C的移动而变化
第II卷(非选择题)
二、填空题(每题5分,共20分)
11.命题“菱形是对角线互相垂直的四边形”的逆命题是_______________.
12.如图,已知∠CAE是△ABC的外角,AD∥BC,且AD是∠EAC的平分线,若∠B=71°,则∠BAC的大小是________.
13.如图,三角形ABC的面积是30平方厘米,D是BC的中点,AE的长是ED的长的2倍,那么三角形CDE的面积是 平方厘米.
14.如图所示,∠1=65°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为___________.
三、解答题(共9小题,满分90分)
15.已知三角形的两边长分别为4和6.
(1)试确定三角形第三边长x的取值范围;
(2)若第三边的长为4的倍数,求三角形的周长.
16.如图,在△ABC中,完成下列画图和计算:
(1)作△ABC的角平分线AE和BC边上的高AD;
(2)若∠BAC = 110°,∠C =50°,求∠DAE的度数。
17.如图,是内的一点,连结.
求证.
18.一个零件的形状如图所示,按规定,和分别是32°和21°的零件为合格零件,现质检工人量得,就断定这个零件不合格,请你运用三角形的有关知识说明零件不合格的理由.
19.已知:BP、CP是△ABC的外角的平分线,交于点P. 求证:∠P=90°-∠A
20.在ΔABC中,∠ABC的平分线与∠ACB的外角∠ACE的平分线相交于点D。
⑴.若∠ABC=60°,∠ACB=40°,求∠A和∠D的度数。
⑵.由⑴小题的计算结果,猜想,∠A和∠D有什么数量关系,并加以证明。
21.已知:直线AB∥CD,点E. F分别是AB、CD上的点。
(1)如图1,当点P在AB、CD内部时,试说明:∠EPF=∠AEP+∠CFP;
(2)如图2,当点P在AB上方时,∠EPF、∠AEP、∠CFP之间有怎样的数量关系?并说明理由。
22.(1)如图①∠1+∠2与∠B+∠C有什么关系?为什么?
(2)把图①△ABC沿DE折叠,得到图②,填空:
∠1+∠2 ∠B+∠C(填“>”“<”“=”),当∠A=60°时,∠B+∠C+∠1+∠2=
(3)如图③,是由图①的△ABC沿DE折叠得到的,猜想∠BDA+∠CEA与∠A的关系,并证明你的猜想.
23.如图,在中,,若是和的平分线交点,求的度数。
若是内任意一点,试探究与之间的关系,并说明理由
请你直接利用以上结论,解决以下问题:
①图中点为内任意一点,若则
②如图平分平分,若,求的度数.
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案
1.B
【解析】
试题解析:∵∠A=∠B=∠C,
∴设∠A=x,则∠B=2x,∠C=3x,
∵三角形的内角和是180°,
∴x+2x+3x=180°,解得x=30°,
∴∠C=3x=90°,
∴此三角形是直角三角形.
2.A
【解析】∵三角形的三边长分别为4,7,x,∴7-4<x<7+4,即3<x<11,
故选A.
3.D
【解析】对于D相等的角可以是对顶角,也可以是同位角,所以D错误。所以选D。
4.B
【解析】
解:①根据三角形的角平分线的概念,知AG是△ABE的角平分线,故此说法错误;
②根据三角形的中线的概念,知BG是△ABD的边AD上的中线,故此说法错误;
③根据三角形的高的概念,知CH为△ACD的边AD上的高,故此说法正确;
④根据三角形的角平分线和高的概念,知AH是△ACF的角平分线和高线,故此说法正确.
故选B.
点睛:本题考查了三角形的角平分线、三角形的中线、三角形的高的概念,注意:三角形的角平分线、中线、高都是线段,且都是顶点和三角形的某条边相交的交点之间的线段.透彻理解定义是解题的关键.
5.D
【解析】
分5是腰长与底边长两种情况讨论:①5是腰长时,三边分别为5、5、6时,能组成三角形,周长=5+5+6=16;②5是底边时,三边分别为5、6、6,能组成三角形,周长=5+6+6=17.
综上所述,等腰三角形的周长为16或17.故选D.
6.D
【解析】
【分析】
由∠1,∠2的度数,利用邻补角互补可求出∠ABC,∠BAC的度数,再利用三角形的外角性质即可求出∠3的度数.
【详解】
解:∵∠1=∠2=150°,
∴∠ABC=∠BAC=180°-150°=30°,
∴∠3=∠ABC+∠BAC=60°.
故选:D.
【点睛】
本题考查了三角形的外角性质以及邻补角,牢记“三角形的一个外角等于和它不相邻的两个内角的和”是解题的关键.
7.C
【解析】
【分析】
利用三角形内角和定理求解即可.
【详解】
因为三角形内角和为180°,且∠A = 60°,∠B = 75°,所以∠C=180°–60°–75°=45°.
【点睛】
三角形内角和定理是常考的知识点.
8.B
【解析】解:∵到三角形三边距离相等的点是三角形三条角平分线的交点,
∴点P应是△ABC的三条角平分线的交点.
故选B.
9.C
【解析】
如图,
∵∠1=90°-60°=30°,
∴∠α=45°+30°=75°。故选C。
10.B
【解析】
试题解析:∵CD平分∠ACB,BE平分∠MBC,
∴∠ACB=2∠DCB,∠MBC=2∠CBE,
∵∠MBC=2∠CBE=∠A+∠ACB,∠CBE=∠D+∠DCB,
∴2∠CBE=∠D+∠DCB,
∴∠MBC=2∠D+∠ACB,
∴2∠D+∠ACB=∠A+∠ACB,
∴∠A=2∠D,
∵∠A=100°,
∴∠D=50°.
故选B.
11.对角线互相垂直的四边形是菱形
【解析】分析:把一个命题的条件和结论互换就得到它的逆命题.
详解:命题“菱形是对角线互相垂直的四边形”的逆命题是“对角线互相垂直的四边形是菱形”.
点睛:本题考查了互逆命题的知识,两个命题中,如果第一个命题的条件是第二个命题的结论,而第一个命题的结论又是第二个命题的条件,那么这两个命题叫做互逆命题.其中一个命题称为另一个命题的逆命题.
12.38°
【解析】
试题分析:由AD∥BC可得∠EAD=∠B=71°,由AD是的平分线可得∠EAC=2∠EAD=2×71°=142°,则∠BAC=180°–=180°–142°=38°.
考点:三角形的外角性质;平行线的性质.
13.5
【解析】
解:S△ABD=S△ADC=S△ABC=×30=15(平方厘米);
S△CAE:S△CDE=2:1,
S△CDE=S△ADC=×15=5(平方厘米);
答:三角形CDE的面积是5平方厘米.
14.230°
【解析】
【分析】
依据三角形内角和定理,即可得到∠B+∠C=115°,∠MGH+∠MHG=115°,再根据三角形外角性质,即可得出∠A+∠B+∠C+∠D+∠E+∠F的度数.
【详解】
如图所示,
∵∠1=∠BMC=65°,
∴∠B+∠C=180°?65°=115°,∠MGH+∠MHG=115°,
又∵∠MGH是△DFG的外角,∠MHG是△AEH的外角,
∴∠MGH=∠F+∠D,∠MHG=∠A+∠E,
∴∠F+∠D+∠A+∠E=∠MGH+∠MHG=115°,
∴∠A+∠B+∠C+∠D+∠E+∠F=115°+115°=230°,
故答案为:230°.
【点睛】
本题考查了三角形的外角和三角形的内角和的相关知识,解决本题的关键是利用三角形外角性质:三角形的一个外角等于和它不相邻的两个内角的和.
15.(1) 2
本题解析:
(1)由三角形三边关系,得x>6-4且x<6+4,即x>2且x<10.所以2
16.(1)见解析;(2)15°
【解析】
【分析】
(1)根据角平分线及垂线的画法作图即可;
(2)利用角平分线把一个角平分的性质和高线得到90°的性质可得∠DAE的度数.
【详解】
(1)如图,
(2)解:∵ AE平分∠BAC,∠BAC=110°,
∴∠CAC=∠BAC=55° ,
∵ AD是BC边上的高,
∴∠ADC=90° ,
∵∠C=50°,
∴∠CAD=180°- ∠C- ∠ADC=40°,
∴∠EAD=∠CAE- ∠CAD=15°.
【点睛】
本题考查了三角形的高与角平分线的画法;求三角形同一顶点处的高线与角平分线的夹角注意运用角平分线的性质,高线的性质,以及三角形内角和定理.
17.见解析
【解析】
【分析】
延长BP交AC于点D,在△ABD中可得OB+OD<AB+AD,在△OCD中,OC<OD+CD然后把两个不等式相加整理后可得结论.
【详解】
证明:延长BO交AC于点D,
在△ABD中,OB+OD<AB+AD①,
在△OCD中,OC<OD+CD②,
①+②得OB+OD+OC<AB+AD+OD+CD,
即OB+OC<AB+AC,
即:.
【点睛】
此题考查三角形的三边关系,关键是熟练掌握三角形的三边关系定理:两边之和大于第三边.
18.零件不合格,理由详见解析
【解析】
【分析】
按题意作出四边形ABDC,再想办法利用三角形关于角的性质验证,验证的关键在于找出∠BDC与∠A、∠B、∠C之间的关系.
【详解】
连接AD,并延长至点E.
由于∠CDE=∠CAD+∠C,∠BDE=∠BAD+∠B,
所以∠CDE+∠BDE=∠CAD+∠C+∠BAD+∠B,
即∠CDB=∠BAC+∠B+∠C.
如果零件合格,那么∠CDB=90°+32°+21°=143°,
而现量得∠BDC=149°.
故零件不合格.
【点睛】
此题考查三角形内角和定理,三角形的外角性质,解题关键在于掌握各性质定义和作辅助线.
19.见解析.
【解析】
【分析】
利用角平分线的性质和三角形外角的性质得到∠PBC=(∠A+∠ACB),∠PCB=(∠A+∠ABC),然后根据三角形内角和定理得出结论.
【详解】
证明:∵BP、CP分别是△ABC两个外角∠EBC和∠BCF的平分线,
∴∠PBC=∠EBC=(∠A+∠ACB),∠PCB=∠BCF=(∠A+∠ABC),
∴∠P=180°?∠PBC?∠PCB=180°?(∠A+∠ACB+∠A+∠ABC),
∵∠A+∠ACB+∠BAC=180°,
∴∠P=180°?(∠A+180°)=90°?∠A.
【点睛】
此题主要考查了三角形外角的性质、三角形内角和定理以及角平分线的性质,正确应用角平分线的性质是解题关键.
20.(1)∠A=80°,∠D=40°;(2)∠A=2∠D,理由见解析
【解析】
【分析】
(1)根据三角形内角和定理,已知∠ABC=60°,∠ACB=40°,易求∠A,根据角平分线定义和外角的性质即可求得∠D度数.
(2)根据三角形内角和定理以及角平分线性质,先求出∠D的等式,再与∠A比较即可解答.
【详解】
(1)在△ABC中,∠ABC=60°,∠ACB=40°,
∴∠A=180°?∠ABC?∠ACB=80°,
∵BD为∠ABC,CD为∠ACE的角平分线,
∴∠DBC=∠ABC=×60°=30°,
∠ACD= (180°?∠ACB)=×140°=70°,
∴∠D=180°?∠DBC?∠ACB?∠ACD=180°?30°?40°?70°=40°,
∴∠A=80°,∠D=40°;
(2)通过第(1)的计算,得到∠A=2∠D,理由如下:
∵∠ACE=∠A+∠ABC,
∴∠ACD+∠ECD=∠A+∠ABD+∠DBE,∠DCE=∠D+∠DBC,
又∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠DBE,∠ACD=∠ECD,
∴∠A=2(∠DCE?∠DBC),∠D=∠DCE?∠DBC,
∴∠A=2∠D.
【点睛】
此题考查三角形内角和定理,三角形的外角性质,解题关键在于根据角平分线定义和外角的性质即可求得∠D度数.
21.(1)见解析;(2)∠AEP+∠EPF=∠CFP,理由见解析;
【解析】
【详解】
(1) 证明:过P点作PG∥AB,如图1,
∵PG∥AB,
∴∠EPG=∠AEP,
∵AB∥CD,
∴PG∥CD,
∴∠FPG=∠CFP,
∴∠AEP+∠CFP=∠EPF;
(2)∠AEP+∠EPF=∠CFP,理由如下:
∵∠AEP+∠EPF=∠AGP,
∵CD∥AB,
∴∠APG=∠CFP,
∴∠AEP+∠EPF=∠CFP.
【点睛】
此题考查三角形外角的性质以及平行线的性质,解题关键在于作辅助线和利用平行线的性质得到得到∠EPG=∠AEP.
22.(1)∠1+∠2=∠B+∠C;理由见解析;
(2)=;240°
(3)∠BDA+∠CEA=2∠A;理由见解析.
【解析】
【分析】
(1)根据三角形的内角和定理即可推得∠1+∠2与∠B+∠C的关系;
(2)由折叠的性质和(1)的结论可得∠1+∠2与∠B+∠C的关系;当∠A=60°时,先求出∠B+∠C的度数,再利用前者的结论即可得出答案;
(3)如图③,延长BD交CE的延长线于A′,利用三角形的外角的性质即可得出结论:∠BDA+∠CEA=2∠A.
【详解】
解:(1)根据三角形内角是180°,可知:∠1+∠2=180°﹣∠A,∠B+∠C=180°﹣∠A,
∴∠1+∠2=∠B+∠C;
(2)由折叠的性质知:图②的∠1+∠2就是图①的∠1+∠2,而由(1)知:∠1+∠2=∠B+∠C;
∴在图②中有∠1+∠2=∠B+∠C;
当∠A=60°时,∠B+∠C=180°﹣∠A=120°,
∴∠B+∠C+∠1+∠2=120°×2=240°;
故答案为:=;240°
(3)∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
理由如下:如图③,延长BD交CE的延长线于A′,连接AA′.
∵∠BDA=∠DA′A+∠DAA′,∠AEC=∠EA′A+∠EAA′,∠DA′E=∠DAE,
∴∠BDA+∠AEC=2∠DAE,
∴∠BDA+∠CEA与∠A的关系为:∠BDA+∠CEA=2∠A.
【点睛】
本题考查了折叠的性质、三角形的内角和定理与三角形外角的性质,熟练掌握三角形的内角和定理和三角形外角的性质是解此题的关键.
23.(1)∠BDC=125°;(2)∠BDC=∠BAC+∠ABD+∠ACD,理由见解析;(3)①60;②∠DCE=90°.
【解析】
【分析】
(1)根据三角形的内角和与DB平分∠ABC,DC平分∠ACB可求得∠DBC+∠DCB的度数,再在△DBC中应用三角形内角和定理即可求出结果;
(2)作射线AD,再运用三角形的外角性质即可得出结论;
(3)①直接应用(2)的结论计算即可;
②先由(2)的结论求出∠ADB+∠AEB的度数,再由CD平分∠ADB,CE平分∠ACB可求出∠ADC+∠AEC的度数,然后再运用(2)的结论即可求出结果.
【详解】
解:(1)∵∠A=70°,
∴∠ABC+∠ACB=180°-∠A=180°-70°=110°,
∵DB平分∠ABC,DC平分∠ACB,
∴∠DBC=∠ABC,∠DCB=∠ACB,
∴∠DBC+∠DCB=(∠ABC+∠ACB)=×110°=55°,
∴∠BDC=180°-55°=125°;
(2)∠BDC=∠BAC+∠ABD+∠ACD,理由如下:
如图2,作射线AD,∵∠1、∠2分别是△ABD和△ACD的外角,
∴∠1=∠BAD+∠ABD,∠2=∠CAD+∠ACD,
∴∠BDC=∠1+∠2=∠BAD+∠ABD+∠CAD+∠ACD=∠BAC+∠ABD+∠ACD.
(3)①由(2)的结论可得:∠ABD+∠ACD=∠BDC―∠A=110°-50°=60°;故答案为60;
②由(2)的结论可得:∠ADB+∠AEB=∠DBE―∠A=130°-50°=80°;
∵CD平分∠ADB,CE平分∠ACB,
∴∠ADC=∠ADB,∠AEC=∠AEB,
∴∠ADC+∠AEC=(∠ADB+∠AEB)=×80°=40°,
又∵∠DCE=∠ADC+∠A+∠AEC,
∴∠DCE=50°+40°=90°.
【点睛】
本题考查了角平分线的定义、三角形的内角和定理、三角形的外角定理和整体代入求解的数学思想,熟练掌握三角形的内角和定理和外角性质、灵活应用整体代入的数学思想是解题的关键.
答案第1页,总2页
答案第1页,总2页
