北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第26讲 平行四边形的判定定理(提高)含答案
文档属性
| 名称 | 北师大版初中数学八年级下册知识讲解,巩固练习(教学资料,补习资料):第26讲 平行四边形的判定定理(提高)含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 270.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-16 20:57:32 | ||
图片预览


文档简介
平行四边形的判定定理(提高)
【学习目标】
1.平行四边形的四个判定定理及应用,会应用判定定理判断一个四边形是不是平行四边形.
2.会综合应用平行四边形的性质定理和判定定理解决简单的几何问题.
【要点梳理】
要点一、平行四边形的判定
1.两组对边分别平行的四边形是平行四边形;
2.一组对边平行且相等的四边形是平行四边形;
3. 两组对边分别相等的四边形是平行四边形;
4.两组对角分别相等的四边形是平行四边形;
5.对角线互相平分的四边形是平行四边形.
要点诠释:
(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个
行四边形时,应选择较简单的方法.
(2)这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.
【典型例题】
类型一、平行四边形的判定
1、如图,点A、B、C在正方形网格的格点上(小正方形的边长为单位1). (1)在图中确定格点D,并画出以A、B、C、D为顶点的平行四边形. (2)若以C为原点,BC所在直线为x轴,建立直角坐标系,则你确定的点D的坐标是________________.
【思路点拨】(1)分为三种情况:以AC为对角线时、以AB为对角线时、以BC为对角线时,画出图形,根据A、B、C的坐标求出即可; (2)在(1)的基础上,把y轴向左平移了一个单位,根据平移性质求出即可.
【答案与解析】
(1)解:从图中可知A(-3,2),B(-4,0)C(-1,0), 以AB为对角线时,得出平行四边形ACBD1,D1的坐标是(-6,2), 以AC为对角线时,得出平行四边形ABCD2,D2的坐标是(0,2), 以BC为对角线时,得出平行四边形ABD3C,D3的坐标是(-2,-2), (2)解:以C为原点,BC所在直线为x轴,建立直角坐标系,D的坐标是(-1,2),(1,2),(-5,2), 故答案为:(-1,2)或(1,2)或(-5,2).
【总结升华】本题考查了平行四边形的性质和坐标与图形性质的应用,主要考查学生能否运用平行四边形的性质进行计算,注意:一定要进行分类讨论.
举一反三
【变式】(2019?呼伦贝尔)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【答案】
证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴Rt△AFE≌Rt△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
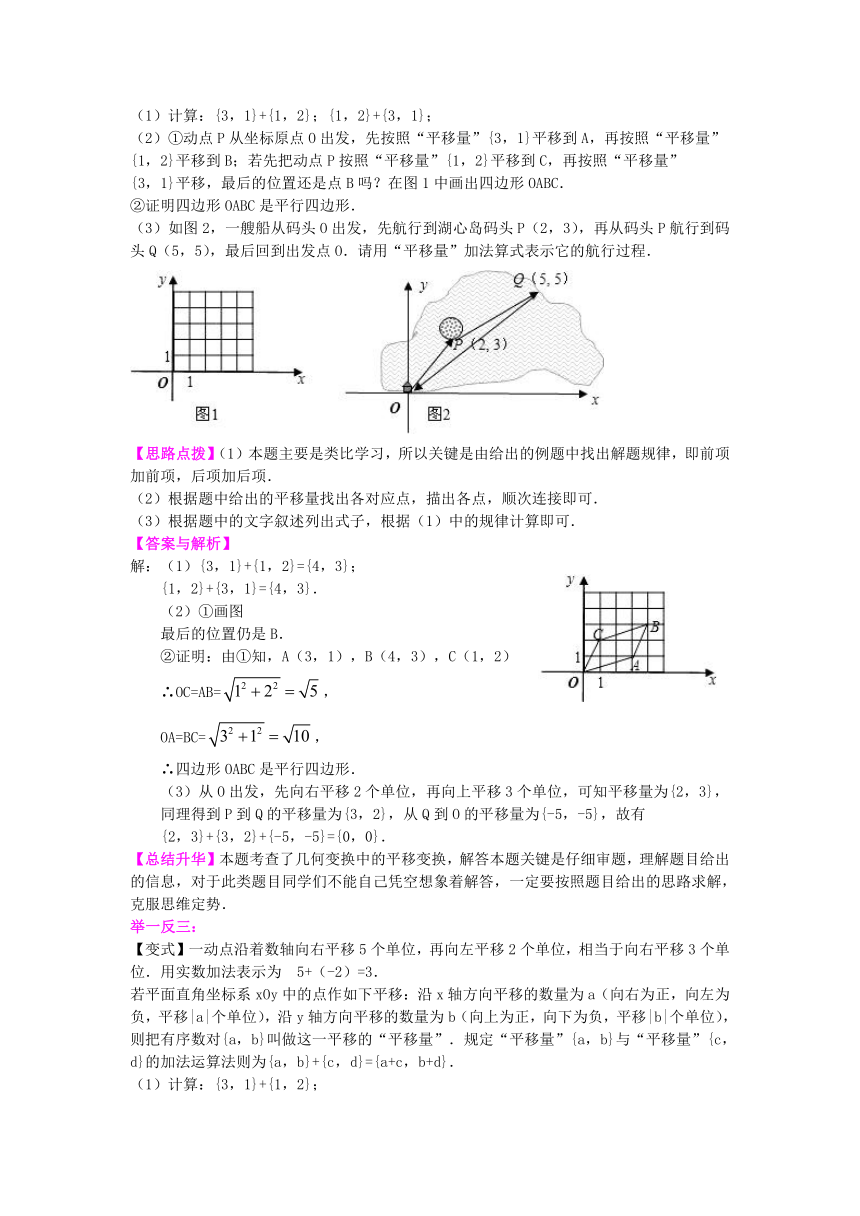
2、类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1. 若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}. 解决问题: (1)计算:{3,1}+{1,2};{1,2}+{3,1}; (2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量” {1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量” {3,1}平移,最后的位置还是点B吗?在图1中画出四边形OABC. ②证明四边形OABC是平行四边形. (3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
【思路点拨】(1)本题主要是类比学习,所以关键是由给出的例题中找出解题规律,即前项加前项,后项加后项. (2)根据题中给出的平移量找出各对应点,描出各点,顺次连接即可. (3)根据题中的文字叙述列出式子,根据(1)中的规律计算即可.
【答案与解析】
解:(1){3,1}+{1,2}={4,3}; {1,2}+{3,1}={4,3}. (2)①画图 最后的位置仍是B. ②证明:由①知,A(3,1),B(4,3),C(1,2) ∴OC=AB=, OA=BC=, ∴四边形OABC是平行四边形. (3)从O出发,先向右平移2个单位,再向上平移3个单位,可知平移量为{2,3}, 同理得到P到Q的平移量为{3,2},从Q到O的平移量为{-5,-5},故有 {2,3}+{3,2}+{-5,-5}={0,0}.
【总结升华】本题考查了几何变换中的平移变换,解答本题关键是仔细审题,理解题目给出的信息,对于此类题目同学们不能自己凭空想象着解答,一定要按照题目给出的思路求解,克服思维定势.
举一反三:
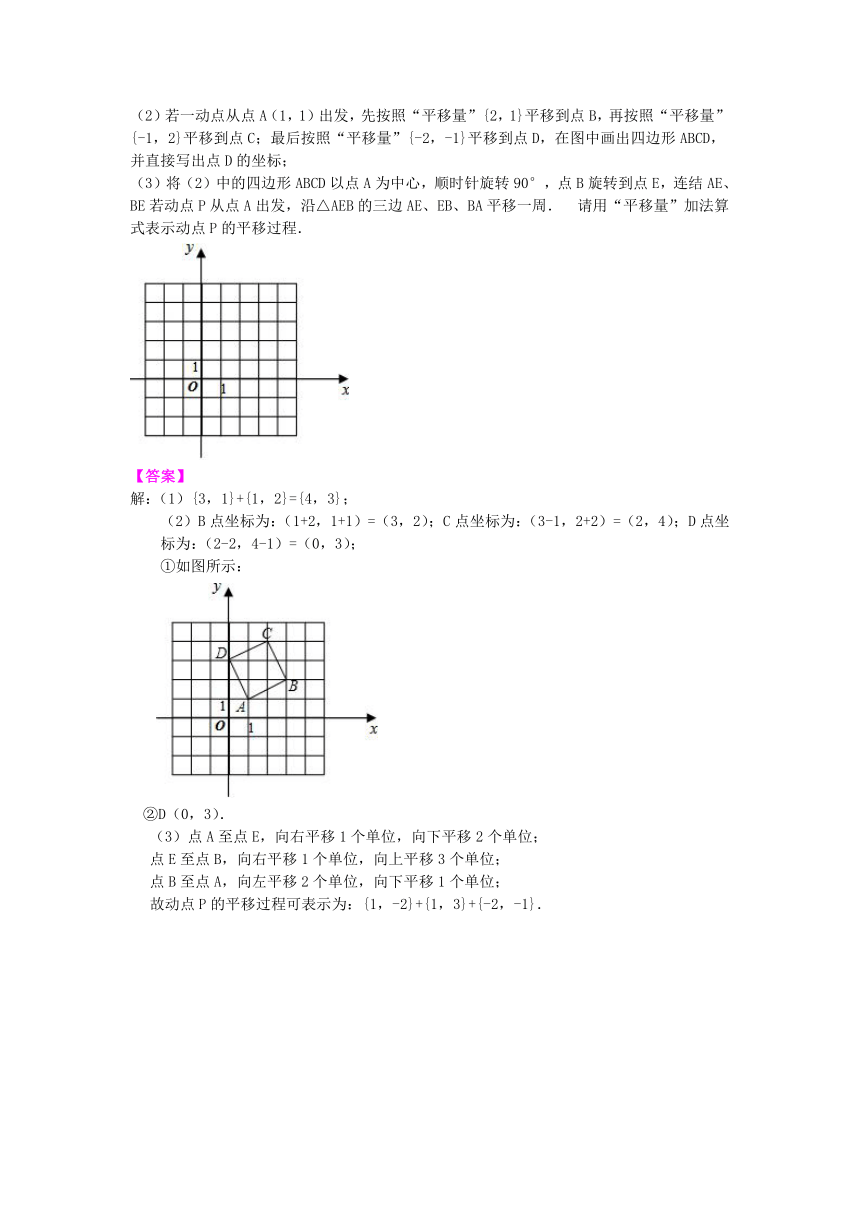
【变式】一动点沿着数轴向右平移5个单位,再向左平移2个单位,相当于向右平移3个单位.用实数加法表示为?5+(-2)=3. 若平面直角坐标系xOy中的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.规定“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}. (1)计算:{3,1}+{1,2}; (2)若一动点从点A(1,1)出发,先按照“平移量”{2,1}平移到点B,再按照“平移量” {-1,2}平移到点C;最后按照“平移量”{-2,-1}平移到点D,在图中画出四边形ABCD,并直接写出点D的坐标; (3)将(2)中的四边形ABCD以点A为中心,顺时针旋转90°,点B旋转到点E,连结AE、BE若动点P从点A出发,沿△AEB的三边AE、EB、BA平移一周.?请用“平移量”加法算式表示动点P的平移过程.
【答案】
解:(1){3,1}+{1,2}={4,3}; (2)B点坐标为:(1+2,1+1)=(3,2);C点坐标为:(3-1,2+2)=(2,4);D点坐标为:(2-2,4-1)=(0,3); ①如图所示:
②D(0,3).
(3)点A至点E,向右平移1个单位,向下平移2个单位; 点E至点B,向右平移1个单位,向上平移3个单位; 点B至点A,向左平移2个单位,向下平移1个单位; 故动点P的平移过程可表示为:{1,-2}+{1,3}+{-2,-1}.
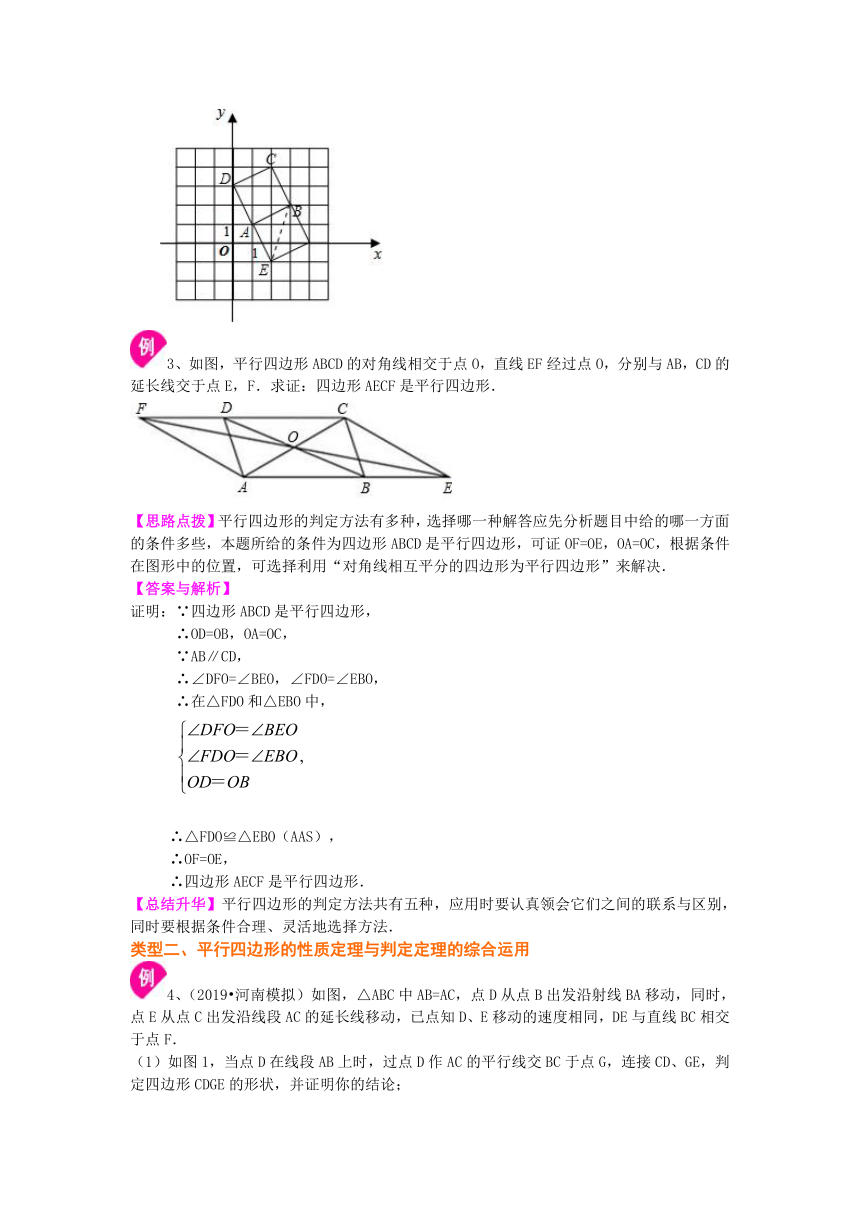
3、如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
【思路点拨】平行四边形的判定方法有多种,选择哪一种解答应先分析题目中给的哪一方面的条件多些,本题所给的条件为四边形ABCD是平行四边形,可证OF=OE,OA=OC,根据条件在图形中的位置,可选择利用“对角线相互平分的四边形为平行四边形”来解决.
【答案与解析】
证明:∵四边形ABCD是平行四边形, ∴OD=OB,OA=OC, ∵AB∥CD, ∴∠DFO=∠BEO,∠FDO=∠EBO, ∴在△FDO和△EBO中,
∴△FDO≌△EBO(AAS), ∴OF=OE, ∴四边形AECF是平行四边形.
【总结升华】平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
类型二、平行四边形的性质定理与判定定理的综合运用
4、(2019?河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
【思路点拨】(1)由题意得出BD=CE,由平行线的性质得出∠DGB=∠ACB,由等腰三角形的性质得出∠B=∠ACB,得出∠B=∠DGB,证出BD=GD=CE,即可得出结论;
(2)由(1)得:BD=GD=CE,由等腰三角形的三线合一性质得出BM=GM,由平行线得出GF=CF,即可得出结论.
【答案与解析】
解:(1)四边形CDGE是平行四边.理由如下:如图1所示:
∵D、E移动的速度相同,
∴BD=CE,
∵DG∥AE,
∴∠DGB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DGB,
∴BD=GD=CE,
又∵DG∥CE,
∴四边形CDGE是平行四边形;
(2)BM+CF=MF;理由如下:如图2所示:
由(1)得:BD=GD=CE,
∵DM⊥BC,
∴BM=GM,
∵DG∥AE,
∴GF=CF,
∴BM+CF=GM+GF=MF.
【总结升华】本题考查了等腰三角形的判定与性质、平行四边形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
举一反三
【变式】如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F. (1)求证:BE=DF; (2)若?M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).
【答案】
解:(1)∵四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD, ∴∠ABD=∠CDB, ∵AE⊥BD于E,CF⊥BD于F, ∴∠AEB=∠CFD=90°, ∴△ABE≌△CDF(AAS), ∴BE=DF;
(2)四边形MENF是平行四边形. 证明:由(1)可知:BE=DF, ∵四边形ABCD为平行四边形, ∴AD∥BC, ∴∠MDB=∠NBD, ∵DM=BN, ∴△DMF≌△BNE, ∴NE=MF,∠MFD=∠NEB, ∴∠MFE=∠NEF, ∴MF∥NE, ∴四边形MENF是平行四边形.
5、如图,已知在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG. (1)求证:四边形GEHF是平行四边形; (2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
【思路点拨】(1)先由平行四边形的性质,得AB=CD,AB∥CD,根据两直线平行内错角相等得∠GBE=∠HDF.再由SAS可证△GBE≌△HDF,利用全等的性质,证明∠GEF=∠HFE,从而得GE∥HF,又GE=HF,运用一组对边平行且相等的四边形是平行四边形得证. (2)仍成立.可仿照(1)的证明方法进行证明.
【答案与解析】
(1)证明:∵四边形ABCD是平行四边形, ∴AB=CD,AB∥CD,∴∠GBE=∠HDF. 又∵AG=CH,∴BG=DH. 又∵BE=DF,∴△GBE≌△HDF. ∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE, ∴GE∥HF,∴四边形GEHF是平行四边形.
(2)解:仍成立.(证法同上)
【总结升华】本题考查的知识点为:一组对边平行且相等的四边形是平行四边形.
举一反三
【变式】如图,ABCD中,对角线AC,BD相交于O点,AE⊥BD于E,CF⊥BD于F,BG⊥AG于G,DH⊥AC于H.求证:四边形GEHF是平行四边形.
【答案】
证明:∵四边形ABCD是平行四边形, ∴BO=DO,AO=CO,AB=CD,AB∥CD, ∴∠ABD=∠CDB, ∵AE⊥BD于E,CF⊥BD于F, ∴∠AEB=∠CFD=90°, 在△ABE和△CDF中,
∴△ABE≌△CDF(AAS), ∴BE=DF, ∴BO-BE=DO-DF, 即:EO=FO, 同理:△ABG≌△CDH, ∴AG=CH, ∴AO-AG=CO-CH, 即:GO=OH, ∴四边形GEHF是平行四边形.
【巩固练习】
一.选择题
1.如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )
A.(3,-1) B.(-1,-1) C.(1,1) D.(-2,-1)
2.以不共线的三点A、B、C为顶点的平行四边形共有( )个.
A.1 B.2 C.3 D.无数
3.A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个中任选两个作为条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
4. (2019春?海南校级月考)如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
5. 如图,在ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
A. AE=CF B.DE=BF
C. D.
6.(杭州模拟)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2;
④四边形ACEB的面积是16.
则以上结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②④
二.填空题
7.已知四边形ABCD的对角线相交于O,给出下列5个条件①AB∥CD?②AD∥BC③AB=CD?④∠BAD=∠DCB,从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有____________组.
8.在?ABCD中,对角线相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=AB,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO其中能够判定ABCD是平行四边形的有____________.
9.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可以找出______个平行四边形.
10.如图,已知AB=CD,AD=CB,则∠ABC+∠BAD=___________度.
11.(2019春?太原期末)如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,若要使四边形是平行四边形,则需要添加的一个条件是 .(只写出一种情况即可)
12.(2019春?成都校级期末)如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
三.解答题
13. 在ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
14.(2019?镇江二模)如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
15. 如图所示,已知△ABC是等边三角形,D、F两点分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
【答案与解析】
一.选择题
1.【答案】D;
【解析】A、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(3,-1)时, ∴BO=AC1=2, ∵A,C1,两点纵坐标相等, ∴BO∥AC1, ∴四边形OAC1B是平行四边形;故此选项正确; B、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(-1,-1)时, ∴BO=AC2=2, ∵A,C2,两点纵坐标相等, ∴BO∥AC2, ∴四边形OC2AB是平行四边形;故此选项正确; C、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(1,1)时, ∴BO=AC1=2, ∵A,C1,两点纵坐标相等, ∴C3O=BC3=, 同理可得出AO=AB=, 进而得出C3O=BC3=AO=AB,∠OAB=90°, ∴四边形OABC3是正方形;故此选项正确; D、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(-1,-1)时,四边形OC2AB是平行四边形; ∴当第四个点为(-2,-1)时,四边形OC2AB不可能是平行四边形; 故此选项错误.故选:D.
2.【答案】C;
【解析】分别以AB,BC,AC为对角线作平行四边形.
3.【答案】C;
【解析】根据平行四边形的判定,可以有四种:①与②,③与④,①与③,②与④都能判定四边形是平行四边形,故选C.
4.【答案】B;
【解析】设EF与NH交于点O,∵在?ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边AEOH、DHOF、BEON、CFON、AEFD、BEFC、AHNB、DHNC
和ABCD都是平行四边形,共9个.
故选B.
5.【答案】B;
【解析】C选项和D选项均可证明△ADE≌△CBF,从而得到AE=CF,EO=FO,BO=DO,所以可证四边形DEBF是平行四边形.
6.【答案】A;
【解析】解:①∵∠ACB=90°,DE⊥BC,
∴∠ACD=∠CDE=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,故①正确;
②∵D是BC的中点,DE⊥BC,
∴EC=EB,
∴△BCE是等腰三角形,故②正确;
③∵AC=2,∠ADC=30°,
∴AD=4,CD=2,
∵四边形ACED是平行四边形,
∴CE=AD=4,
∵CE=EB,
∴EB=4,DB=2,
∴CB=4,
∴AB==2,
∴四边形ACEB的周长是10+2故③正确;
④四边形ACEB的面积:×2×4+×4×2=8,故④错误,
故选:A.
二.填空题
7.【答案】4;
【解析】①和②根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形; ①和③根据一组对边平行且相等的四边形是平行四边形,能推出四边形ABCD为平行四边形; ①和④,②和④根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形; 所以能推出四边形ABCD为平行四边形的有四组.故答案为:4.
8.【答案】①②③④;
【解析】∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形,∴①正确; ∵AD=BC,AD∥BC, ∴四边形ABCD是平行四边形,∴②正确; ∵AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形,∴③正确; ∵AO=CO,BO=DO, ∴四边形ABCD是平行四边形,∴④正确; 即其中能判定四边形ABCD是平行四边形的有①②③④, 故答案为:①②③④.
9.【答案】15;
【解析】两个全等的等边三角形,以一边为对角线构成的四边形是平行四边形,这样的两个平行四边形又可组成较大的平行四边形,从该图案中可以找出15个平行四边形. 故答案为:15.
10.【答案】180°;
【解析】依题意得ABCD是平行四边形, ∴AD∥BC, ∴∠ABC+∠BAD=180°.
11.【答案】AD=BC;
【解析】∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,
故答案为:AD=BC.
12.【答案】6;
【解析】解:∵在△ABC中,AB=3,AC=4,BC=5,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证△ABC≌△EFC,
∴AB=EF=AD=3,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=30°,
∴S口AEFD=AD?(DF×)=3×(4×)=6.
即四边形AEFD的面积是6.
故答案为:6.
二.解答题
13.【解析】
证明:在ABCD中
AD∥BC,AO=CO,BO=DO
∴∠GAO=∠HCO
在△AGO和△CHO中
∴△AGO≌△CHO
∴GO=HO
又∵BO=DO,BE=DF
∴EO=FO
∴四边形EHFG为平行四边形.
14.【解析】
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
,
∴△ACE≌△DBF(AAS);
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.
15.【解析】
证明:(1)∵ △ABC是等边三角形,
∴ ∠ABC=60°.
又∵ ∠EFB=60°,
∴ EF∥BC,即EF∥DC.
又∵ DC=EF,
∴ 四边形EFCD是平行四边形.
(2)如图,连接BE.
∵ BF=EF,∠EFB=60°,
∴ △EFB是等边三角形,
∴ BE=BF=EF,∠EBF=60°,
∴ DC=EF=BE.
∵ △ABC是等边三角形,
∴ AC=AB,∠ACD=60°.
在△ABE和△ACD中,
∵ AB=AC,∠ABE=∠ACD,BE=CD,
∴ △ABE≌△ACD,
∴ AE=AD.
【学习目标】
1.平行四边形的四个判定定理及应用,会应用判定定理判断一个四边形是不是平行四边形.
2.会综合应用平行四边形的性质定理和判定定理解决简单的几何问题.
【要点梳理】
要点一、平行四边形的判定
1.两组对边分别平行的四边形是平行四边形;
2.一组对边平行且相等的四边形是平行四边形;
3. 两组对边分别相等的四边形是平行四边形;
4.两组对角分别相等的四边形是平行四边形;
5.对角线互相平分的四边形是平行四边形.
要点诠释:
(1)这些判定方法是学习本章的基础,必须牢固掌握,当几种方法都能判定同一个
行四边形时,应选择较简单的方法.
(2)这些判定方法既可作为判定平行四边形的依据,也可作为“画平行四边形”的依据.
【典型例题】
类型一、平行四边形的判定
1、如图,点A、B、C在正方形网格的格点上(小正方形的边长为单位1). (1)在图中确定格点D,并画出以A、B、C、D为顶点的平行四边形. (2)若以C为原点,BC所在直线为x轴,建立直角坐标系,则你确定的点D的坐标是________________.
【思路点拨】(1)分为三种情况:以AC为对角线时、以AB为对角线时、以BC为对角线时,画出图形,根据A、B、C的坐标求出即可; (2)在(1)的基础上,把y轴向左平移了一个单位,根据平移性质求出即可.
【答案与解析】
(1)解:从图中可知A(-3,2),B(-4,0)C(-1,0), 以AB为对角线时,得出平行四边形ACBD1,D1的坐标是(-6,2), 以AC为对角线时,得出平行四边形ABCD2,D2的坐标是(0,2), 以BC为对角线时,得出平行四边形ABD3C,D3的坐标是(-2,-2), (2)解:以C为原点,BC所在直线为x轴,建立直角坐标系,D的坐标是(-1,2),(1,2),(-5,2), 故答案为:(-1,2)或(1,2)或(-5,2).
【总结升华】本题考查了平行四边形的性质和坐标与图形性质的应用,主要考查学生能否运用平行四边形的性质进行计算,注意:一定要进行分类讨论.
举一反三
【变式】(2019?呼伦贝尔)如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE,已知:∠BAC=30°,EF⊥AB,垂足为F,连接DF.
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
【答案】
证明:(1)∵Rt△ABC中,∠BAC=30°,
∴AB=2BC,
又∵△ABE是等边三角形,EF⊥AB,
∴AB=2AF
∴AF=BC,
在Rt△AFE和Rt△BCA中,
,
∴Rt△AFE≌Rt△BCA(HL),
∴AC=EF;
(2)∵△ACD是等边三角形,
∴∠DAC=60°,AC=AD,
∴∠DAB=∠DAC+∠BAC=90°
又∵EF⊥AB,
∴EF∥AD,
∵AC=EF,AC=AD,
∴EF=AD,
∴四边形ADFE是平行四边形.
2、类比学习:一动点沿着数轴向右平移3个单位,再向左平移2个单位,相当于向右平移1个单位.用实数加法表示为3+(-2)=1. 若坐标平面上的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”;“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}. 解决问题: (1)计算:{3,1}+{1,2};{1,2}+{3,1}; (2)①动点P从坐标原点O出发,先按照“平移量”{3,1}平移到A,再按照“平移量” {1,2}平移到B;若先把动点P按照“平移量”{1,2}平移到C,再按照“平移量” {3,1}平移,最后的位置还是点B吗?在图1中画出四边形OABC. ②证明四边形OABC是平行四边形. (3)如图2,一艘船从码头O出发,先航行到湖心岛码头P(2,3),再从码头P航行到码头Q(5,5),最后回到出发点O.请用“平移量”加法算式表示它的航行过程.
【思路点拨】(1)本题主要是类比学习,所以关键是由给出的例题中找出解题规律,即前项加前项,后项加后项. (2)根据题中给出的平移量找出各对应点,描出各点,顺次连接即可. (3)根据题中的文字叙述列出式子,根据(1)中的规律计算即可.
【答案与解析】
解:(1){3,1}+{1,2}={4,3}; {1,2}+{3,1}={4,3}. (2)①画图 最后的位置仍是B. ②证明:由①知,A(3,1),B(4,3),C(1,2) ∴OC=AB=, OA=BC=, ∴四边形OABC是平行四边形. (3)从O出发,先向右平移2个单位,再向上平移3个单位,可知平移量为{2,3}, 同理得到P到Q的平移量为{3,2},从Q到O的平移量为{-5,-5},故有 {2,3}+{3,2}+{-5,-5}={0,0}.
【总结升华】本题考查了几何变换中的平移变换,解答本题关键是仔细审题,理解题目给出的信息,对于此类题目同学们不能自己凭空想象着解答,一定要按照题目给出的思路求解,克服思维定势.
举一反三:
【变式】一动点沿着数轴向右平移5个单位,再向左平移2个单位,相当于向右平移3个单位.用实数加法表示为?5+(-2)=3. 若平面直角坐标系xOy中的点作如下平移:沿x轴方向平移的数量为a(向右为正,向左为负,平移|a|个单位),沿y轴方向平移的数量为b(向上为正,向下为负,平移|b|个单位),则把有序数对{a,b}叫做这一平移的“平移量”.规定“平移量”{a,b}与“平移量”{c,d}的加法运算法则为{a,b}+{c,d}={a+c,b+d}. (1)计算:{3,1}+{1,2}; (2)若一动点从点A(1,1)出发,先按照“平移量”{2,1}平移到点B,再按照“平移量” {-1,2}平移到点C;最后按照“平移量”{-2,-1}平移到点D,在图中画出四边形ABCD,并直接写出点D的坐标; (3)将(2)中的四边形ABCD以点A为中心,顺时针旋转90°,点B旋转到点E,连结AE、BE若动点P从点A出发,沿△AEB的三边AE、EB、BA平移一周.?请用“平移量”加法算式表示动点P的平移过程.
【答案】
解:(1){3,1}+{1,2}={4,3}; (2)B点坐标为:(1+2,1+1)=(3,2);C点坐标为:(3-1,2+2)=(2,4);D点坐标为:(2-2,4-1)=(0,3); ①如图所示:
②D(0,3).
(3)点A至点E,向右平移1个单位,向下平移2个单位; 点E至点B,向右平移1个单位,向上平移3个单位; 点B至点A,向左平移2个单位,向下平移1个单位; 故动点P的平移过程可表示为:{1,-2}+{1,3}+{-2,-1}.
3、如图,平行四边形ABCD的对角线相交于点O,直线EF经过点O,分别与AB,CD的延长线交于点E,F.求证:四边形AECF是平行四边形.
【思路点拨】平行四边形的判定方法有多种,选择哪一种解答应先分析题目中给的哪一方面的条件多些,本题所给的条件为四边形ABCD是平行四边形,可证OF=OE,OA=OC,根据条件在图形中的位置,可选择利用“对角线相互平分的四边形为平行四边形”来解决.
【答案与解析】
证明:∵四边形ABCD是平行四边形, ∴OD=OB,OA=OC, ∵AB∥CD, ∴∠DFO=∠BEO,∠FDO=∠EBO, ∴在△FDO和△EBO中,
∴△FDO≌△EBO(AAS), ∴OF=OE, ∴四边形AECF是平行四边形.
【总结升华】平行四边形的判定方法共有五种,应用时要认真领会它们之间的联系与区别,同时要根据条件合理、灵活地选择方法.
类型二、平行四边形的性质定理与判定定理的综合运用
4、(2019?河南模拟)如图,△ABC中AB=AC,点D从点B出发沿射线BA移动,同时,点E从点C出发沿线段AC的延长线移动,已点知D、E移动的速度相同,DE与直线BC相交于点F.
(1)如图1,当点D在线段AB上时,过点D作AC的平行线交BC于点G,连接CD、GE,判定四边形CDGE的形状,并证明你的结论;
(2)过点D作直线BC的垂线垂足为M,当点D、E在移动的过程中,线段BM、MF、CF有何数量关系?请直接写出你的结论.
【思路点拨】(1)由题意得出BD=CE,由平行线的性质得出∠DGB=∠ACB,由等腰三角形的性质得出∠B=∠ACB,得出∠B=∠DGB,证出BD=GD=CE,即可得出结论;
(2)由(1)得:BD=GD=CE,由等腰三角形的三线合一性质得出BM=GM,由平行线得出GF=CF,即可得出结论.
【答案与解析】
解:(1)四边形CDGE是平行四边.理由如下:如图1所示:
∵D、E移动的速度相同,
∴BD=CE,
∵DG∥AE,
∴∠DGB=∠ACB,
∵AB=AC,
∴∠B=∠ACB,
∴∠B=∠DGB,
∴BD=GD=CE,
又∵DG∥CE,
∴四边形CDGE是平行四边形;
(2)BM+CF=MF;理由如下:如图2所示:
由(1)得:BD=GD=CE,
∵DM⊥BC,
∴BM=GM,
∵DG∥AE,
∴GF=CF,
∴BM+CF=GM+GF=MF.
【总结升华】本题考查了等腰三角形的判定与性质、平行四边形的判定与性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.
举一反三
【变式】如图,已知四边形ABCD为平行四边形,AE⊥BD于E,CF⊥BD于F. (1)求证:BE=DF; (2)若?M、N分别为边AD、BC上的点,且DM=BN,试判断四边形MENF的形状(不必说明理由).
【答案】
解:(1)∵四边形ABCD是平行四边形, ∴ AB=CD,AB∥CD, ∴∠ABD=∠CDB, ∵AE⊥BD于E,CF⊥BD于F, ∴∠AEB=∠CFD=90°, ∴△ABE≌△CDF(AAS), ∴BE=DF;
(2)四边形MENF是平行四边形. 证明:由(1)可知:BE=DF, ∵四边形ABCD为平行四边形, ∴AD∥BC, ∴∠MDB=∠NBD, ∵DM=BN, ∴△DMF≌△BNE, ∴NE=MF,∠MFD=∠NEB, ∴∠MFE=∠NEF, ∴MF∥NE, ∴四边形MENF是平行四边形.
5、如图,已知在ABCD中,E、F是对角线BD上的两点,BE=DF,点G、H分别在BA和DC的延长线上,且AG=CH,连接GE、EH、HF、FG. (1)求证:四边形GEHF是平行四边形; (2)若点G、H分别在线段BA和DC上,其余条件不变,则(1)中的结论是否成立?(不用说明理由)
【思路点拨】(1)先由平行四边形的性质,得AB=CD,AB∥CD,根据两直线平行内错角相等得∠GBE=∠HDF.再由SAS可证△GBE≌△HDF,利用全等的性质,证明∠GEF=∠HFE,从而得GE∥HF,又GE=HF,运用一组对边平行且相等的四边形是平行四边形得证. (2)仍成立.可仿照(1)的证明方法进行证明.
【答案与解析】
(1)证明:∵四边形ABCD是平行四边形, ∴AB=CD,AB∥CD,∴∠GBE=∠HDF. 又∵AG=CH,∴BG=DH. 又∵BE=DF,∴△GBE≌△HDF. ∴GE=HF,∠GEB=∠HFD,∴∠GEF=∠HFE, ∴GE∥HF,∴四边形GEHF是平行四边形.
(2)解:仍成立.(证法同上)
【总结升华】本题考查的知识点为:一组对边平行且相等的四边形是平行四边形.
举一反三
【变式】如图,ABCD中,对角线AC,BD相交于O点,AE⊥BD于E,CF⊥BD于F,BG⊥AG于G,DH⊥AC于H.求证:四边形GEHF是平行四边形.
【答案】
证明:∵四边形ABCD是平行四边形, ∴BO=DO,AO=CO,AB=CD,AB∥CD, ∴∠ABD=∠CDB, ∵AE⊥BD于E,CF⊥BD于F, ∴∠AEB=∠CFD=90°, 在△ABE和△CDF中,
∴△ABE≌△CDF(AAS), ∴BE=DF, ∴BO-BE=DO-DF, 即:EO=FO, 同理:△ABG≌△CDH, ∴AG=CH, ∴AO-AG=CO-CH, 即:GO=OH, ∴四边形GEHF是平行四边形.
【巩固练习】
一.选择题
1.如图,在平面直角坐标系中,以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形,下列各点中不能作为平行四边形第四个顶点坐标的是( )
A.(3,-1) B.(-1,-1) C.(1,1) D.(-2,-1)
2.以不共线的三点A、B、C为顶点的平行四边形共有( )个.
A.1 B.2 C.3 D.无数
3.A,B,C,D在同一平面内,从①AB∥CD,②AB=CD,③BC∥AD,④BC=AD这四个中任选两个作为条件,能使四边形ABCD为平行四边形的选法有( )
A.6种 B.5种 C.4种 D.3种
4. (2019春?海南校级月考)如图,在?ABCD中,EF∥AD,HN∥AB,则图中的平行四边形(不包括四边形ABCD)的个数共有( )
A.9个 B.8个 C.6个 D.4个
5. 如图,在ABCD中, 对角线AC、BD相交于点O. E、F是对角线AC上的两个不同点,当E、F两点满足下列条件时,四边形DEBF不一定是平行四边形( ).
A. AE=CF B.DE=BF
C. D.
6.(杭州模拟)如图,在△ABC中,∠ACB=90°,D是BC的中点,DE⊥BC,CE∥AD,若AC=2,∠ADC=30°,
①四边形ACED是平行四边形;
②△BCE是等腰三角形;
③四边形ACEB的周长是10+2;
④四边形ACEB的面积是16.
则以上结论正确的是( )
A.①②③ B.①②④ C.①③④ D.②④
二.填空题
7.已知四边形ABCD的对角线相交于O,给出下列5个条件①AB∥CD?②AD∥BC③AB=CD?④∠BAD=∠DCB,从以上4个条件中任选2个条件为一组,能推出四边形ABCD为平行四边形的有____________组.
8.在?ABCD中,对角线相交于点O,给出下列条件:①AB=CD,AD=BC,②AD=AB,AD∥BC,③AB∥CD,AD∥BC,④AO=CO,BO=DO其中能够判定ABCD是平行四边形的有____________.
9.如图,用9个全等的等边三角形,按图拼成一个几何图案,从该图案中可以找出______个平行四边形.
10.如图,已知AB=CD,AD=CB,则∠ABC+∠BAD=___________度.
11.(2019春?太原期末)如图,四边形ABCD的对角线AC与BD相交于点O,AD∥BC,若要使四边形是平行四边形,则需要添加的一个条件是 .(只写出一种情况即可)
12.(2019春?成都校级期末)如图,在△ABC中,AB=4,AC=3,BC=5,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积为 .
三.解答题
13. 在ABCD中,对角线BD、AC相交于点O,BE=DF,过点O作线段GH交AD于点G,交BC于点H,顺次连接EH、HF、FG、GE,求证:四边形EHFG是平行四边形.
14.(2019?镇江二模)如图,已知点A、B、C、D在一条直线上,BF、CE相交于O,AE=DF,∠E=∠F,OB=OC.
(1)求证:△ACE≌△DBF;
(2)如果把△DBF沿AD折翻折使点F落在点G,连接BE和CG. 求证:四边形BGCE是平行四边形.
15. 如图所示,已知△ABC是等边三角形,D、F两点分别在线段BC、AB上,∠EFB=60°,DC=EF.
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
【答案与解析】
一.选择题
1.【答案】D;
【解析】A、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(3,-1)时, ∴BO=AC1=2, ∵A,C1,两点纵坐标相等, ∴BO∥AC1, ∴四边形OAC1B是平行四边形;故此选项正确; B、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(-1,-1)时, ∴BO=AC2=2, ∵A,C2,两点纵坐标相等, ∴BO∥AC2, ∴四边形OC2AB是平行四边形;故此选项正确; C、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(1,1)时, ∴BO=AC1=2, ∵A,C1,两点纵坐标相等, ∴C3O=BC3=, 同理可得出AO=AB=, 进而得出C3O=BC3=AO=AB,∠OAB=90°, ∴四边形OABC3是正方形;故此选项正确; D、∵以O(0,0)、A(1,-1)、B(2,0)为顶点,构造平行四边形, 当第四个点为(-1,-1)时,四边形OC2AB是平行四边形; ∴当第四个点为(-2,-1)时,四边形OC2AB不可能是平行四边形; 故此选项错误.故选:D.
2.【答案】C;
【解析】分别以AB,BC,AC为对角线作平行四边形.
3.【答案】C;
【解析】根据平行四边形的判定,可以有四种:①与②,③与④,①与③,②与④都能判定四边形是平行四边形,故选C.
4.【答案】B;
【解析】设EF与NH交于点O,∵在?ABCD中,EF∥AD,HN∥AB,
∴AD∥EF∥BC,AB∥NH∥CD,
则图中的四边AEOH、DHOF、BEON、CFON、AEFD、BEFC、AHNB、DHNC
和ABCD都是平行四边形,共9个.
故选B.
5.【答案】B;
【解析】C选项和D选项均可证明△ADE≌△CBF,从而得到AE=CF,EO=FO,BO=DO,所以可证四边形DEBF是平行四边形.
6.【答案】A;
【解析】解:①∵∠ACB=90°,DE⊥BC,
∴∠ACD=∠CDE=90°,
∴AC∥DE,
∵CE∥AD,
∴四边形ACED是平行四边形,故①正确;
②∵D是BC的中点,DE⊥BC,
∴EC=EB,
∴△BCE是等腰三角形,故②正确;
③∵AC=2,∠ADC=30°,
∴AD=4,CD=2,
∵四边形ACED是平行四边形,
∴CE=AD=4,
∵CE=EB,
∴EB=4,DB=2,
∴CB=4,
∴AB==2,
∴四边形ACEB的周长是10+2故③正确;
④四边形ACEB的面积:×2×4+×4×2=8,故④错误,
故选:A.
二.填空题
7.【答案】4;
【解析】①和②根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形; ①和③根据一组对边平行且相等的四边形是平行四边形,能推出四边形ABCD为平行四边形; ①和④,②和④根据两组对边分别平行的四边形是平行四边形,能推出四边形ABCD为平行四边形; 所以能推出四边形ABCD为平行四边形的有四组.故答案为:4.
8.【答案】①②③④;
【解析】∵AB=CD,AD=BC, ∴四边形ABCD是平行四边形,∴①正确; ∵AD=BC,AD∥BC, ∴四边形ABCD是平行四边形,∴②正确; ∵AB∥CD,AD∥BC, ∴四边形ABCD是平行四边形,∴③正确; ∵AO=CO,BO=DO, ∴四边形ABCD是平行四边形,∴④正确; 即其中能判定四边形ABCD是平行四边形的有①②③④, 故答案为:①②③④.
9.【答案】15;
【解析】两个全等的等边三角形,以一边为对角线构成的四边形是平行四边形,这样的两个平行四边形又可组成较大的平行四边形,从该图案中可以找出15个平行四边形. 故答案为:15.
10.【答案】180°;
【解析】依题意得ABCD是平行四边形, ∴AD∥BC, ∴∠ABC+∠BAD=180°.
11.【答案】AD=BC;
【解析】∵AD=BC,AD∥BC,
∴四边形ABCD是平行四边形,
故答案为:AD=BC.
12.【答案】6;
【解析】解:∵在△ABC中,AB=3,AC=4,BC=5,
∴BC2=AB2+AC2,
∴∠BAC=90°,
∵△ABD,△ACE都是等边三角形,
∴∠DAB=∠EAC=60°,
∴∠DAE=150°.
∵△ABD和△FBC都是等边三角形,
∴∠DBF+∠FBA=∠ABC+∠ABF=60°,
∴∠DBF=∠ABC.
在△ABC与△DBF中,
∴△ABC≌△DBF(SAS),
∴AC=DF=AE=4,
同理可证△ABC≌△EFC,
∴AB=EF=AD=3,
∴四边形DAEF是平行四边形(两组对边分别相等的四边形是平行四边形).
∴∠FDA=180°﹣∠DAE=30°,
∴S口AEFD=AD?(DF×)=3×(4×)=6.
即四边形AEFD的面积是6.
故答案为:6.
二.解答题
13.【解析】
证明:在ABCD中
AD∥BC,AO=CO,BO=DO
∴∠GAO=∠HCO
在△AGO和△CHO中
∴△AGO≌△CHO
∴GO=HO
又∵BO=DO,BE=DF
∴EO=FO
∴四边形EHFG为平行四边形.
14.【解析】
证明:(1)如图1,
∵OB=OC,
∴∠ACE=∠DBF,
在△ACE和△DBF中,
,
∴△ACE≌△DBF(AAS);
(2)如图2,
∵∠ACE=∠DBF,∠DBG=∠DBF,
∴∠ACE=∠DBG,
∴CE∥BG,
∵CE=BF,BG=BF,
∴CE=BG,
∴四边形BGCE是平行四边形.
15.【解析】
证明:(1)∵ △ABC是等边三角形,
∴ ∠ABC=60°.
又∵ ∠EFB=60°,
∴ EF∥BC,即EF∥DC.
又∵ DC=EF,
∴ 四边形EFCD是平行四边形.
(2)如图,连接BE.
∵ BF=EF,∠EFB=60°,
∴ △EFB是等边三角形,
∴ BE=BF=EF,∠EBF=60°,
∴ DC=EF=BE.
∵ △ABC是等边三角形,
∴ AC=AB,∠ACD=60°.
在△ABE和△ACD中,
∵ AB=AC,∠ABE=∠ACD,BE=CD,
∴ △ABE≌△ACD,
∴ AE=AD.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
