人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):第03章 章末检测高二数学(理)
文档属性
| 名称 | 人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):第03章 章末检测高二数学(理) |  | |
| 格式 | zip | ||
| 文件大小 | 806.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-19 23:48:16 | ||
图片预览




文档简介
一、选择题:在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在空间四边形中,
A. B.
C. D.
2.已知a=(-3,2,5),b=(1,x,-1),且a·b=-2,则x的值是
A.6 B.5
C.4 D.3
3.与向量共线的单位向量是
A. B.
C.和 D.和
4.设l1的方向向量为a=(1,2,-2),l2的方向向量为b=(-2,3,m),若l1⊥l2,则实数m的值为
A.3 B.2
C.1 D.
5.已知,,,,则向量与之间的夹角为
A. B.
C. D.以上都不对
6.已知、分别是四面体的棱,的中点,点在线段上,且,设,,,则
A. B.
C. D.
7.设平面上有四个互异的点,,,,已知,则是
A.直角三角形 B.等腰三角形
C.等腰直角三角形 D.等边三角形
8.若正方体ABCD-A1B1C1D1的棱长为a,则平面AB1D1与平面BDC1的距离为
A.a B.a
C.a D.a
9.已知若三个向量不能构成空间的一个基底,则实数的值为
A.0 B.
C.9 D.
10.正三棱柱ABC-A1B1C1的各棱长都为2,E,F分别是AB,A1C1的中点,则EF的长是
A. B.
C. D.
11.已知空间四个点A(1,1,1),B(-4,0,2),C(-3,-1,0),D(-1,0,4),则直线AD与平面ABC所成的角为
A.30° B.45°
C.60° D.90°
12.已知二面角α-l-β的大小为50°,P为空间中任意一点,则过点P且与平面α和平面β所成的角都是25°的直线的条数为
A.2 B.3
C.4 D.5
二、填空题:请将答案填在题中横线上.
13.已知{i,j,k}为单位正交基底,且a=-i+j+3k,b=2i-3j-2k,则向量a+b与向量a-2b的坐标分别为_________________、_________________.
14.已知向量,,若,则_________________.
15.正方体ABCD-A1B1C1D1中,面ABD1与面B1BD1所成角的大小为_________________.
16.在下列命题中:
①若a,b共线,则a,b所在的直线平行;
②若a,b所在的直线是异面直线,则a,b一定不共面;
③若a,b,c三向量两两共面,则a,b,c三向量一定也共面;
④已知三向量a,b,c,则空间任意一个向量p总可以唯一表示为p=xa+yb+zc.
其中不正确的命题为_________________.(填序号)
三、解答题:解答应写出文字说明、证明过程或演算步骤.
17.已知是单位正交基底,设a1=2i-j+k,a2=i+3j-2k,a3=-2i+j-3k,a4=3i+2j+5k,试问是否存在实数a,b,c使a4=aa1+ba2+ca3成立?如果存在,求出a,b,c的值;如果不存在,请说明理由.
18.如图所示,四边形ABCD、四边形ABEF都是平行四边形且不共面,M,N分别是AC,BF的中点,试判断与是否共线.
19.如图,在正方体中,,,,,分别为,,,,的中点,求证:
(1)直线平面;
(2)平面平面.
20.如图,已知PA垂直于正方形ABCD所成平面,M,N分别是AB,PC的中点,且PAAD2.
(1)求M,N两点之间的距离;
(2)求证:MN⊥平面PCD;
(3)求直线PA与MN所成的角.
21.如图,在以A,B,C,D,E,F为顶点的五面体中,面为正方形,,,且二面角与二面角都是.
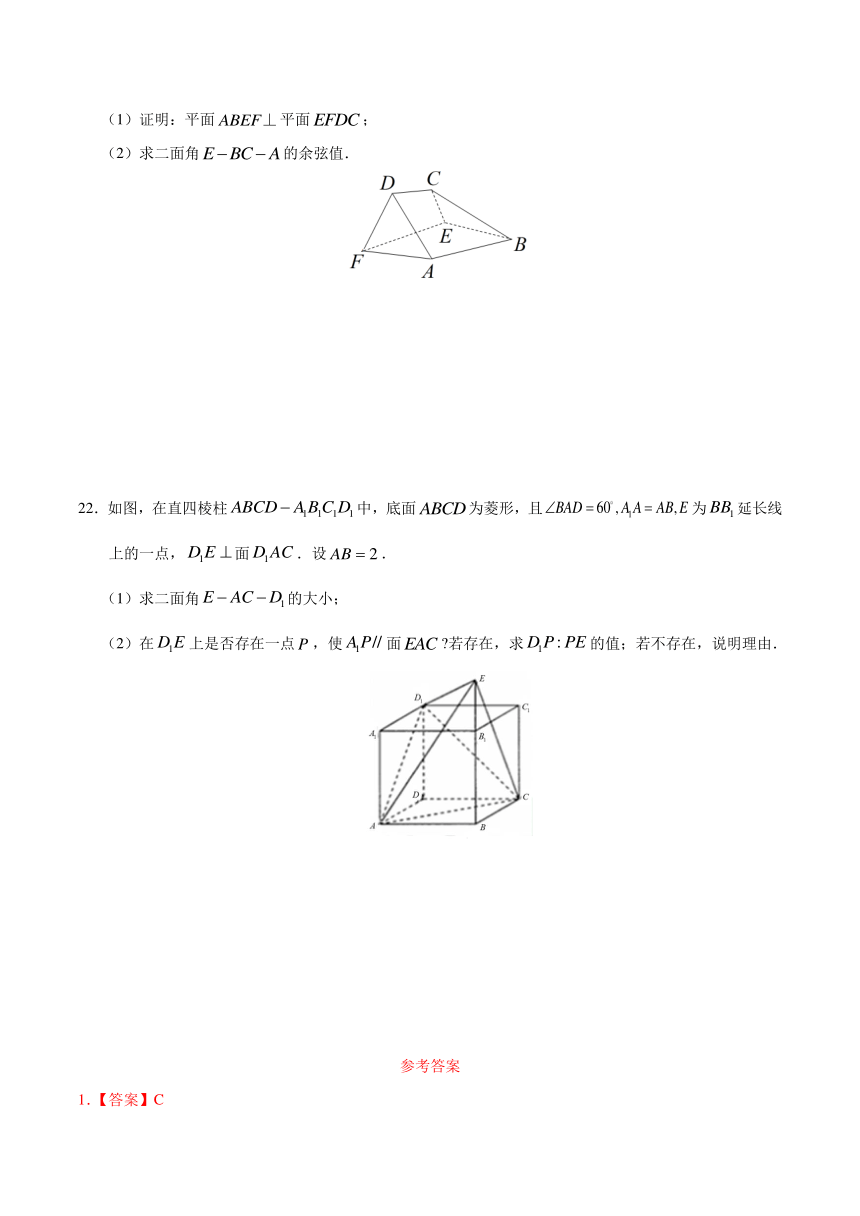
(1)证明:平面平面;
(2)求二面角的余弦值.
22.如图,在直四棱柱中,底面为菱形,且为延长线上的一点,面.设.
(1)求二面角的大小;
(2)在上是否存在一点,使面?若存在,求的值;若不存在,说明理由.
参考答案
1.【答案】C
【解析】.故选C.
2.【答案】D
【解析】a·b=-3+2x-5=-2,∴x=3.故选D.
3.【答案】D
【解析】,∴与a共线的单位向量是(2,3,6),故选D.
4.【答案】B
【解析】∵l1⊥l2,∴a⊥b,∴a·b=0,∴-2+6-2m=0,∴m=2.故选B.
5.【答案】D
【解析】由已知,得,则,由此可得.
从而.故选D.
6.【答案】B
7.【答案】B
【解析】∵,
∴,
∴,故是等腰三角形,故选B.
8.【答案】D
【解析】由正方体的性质易得平面AB1D1∥平面BDC1,则两平面间的距离可转化为点B到平面AB1D1的距离.显然A1C⊥平面AB1D1,以点D为坐标原点,DA,DC,DD1所在直线分别为x轴,y轴,z轴建立空间直角坐标系,则易得平面AB1D1的一个法向量为n=(1,-1,1),A(a,0,0),B(a,a,0),=(0,-a,0),则两平面间的距离为d=.
9.【答案】D
10.【答案】C
【解析】因为,所以
,所以,即
.故选C.
11.【答案】A
【解析】设平面ABC的法向量为,∵,,由及,得
令z=1,得,,∴n=(,,1).,
设AD与平面ABC所成的角为θ,则,
∴θ=30°.故选A.
12.【答案】B
【解析】过点P分别作平面α,β的垂线l1和l2,则l1与l2所成的角为130°或50°,问题转化为过点P与直线l1,l2成65°角的直线有几条,与l1,l2共面的有一条,不共面的有2条.因此,共有3条.故选B.
13.【答案】(1,-2,1) (-5,7,7)
【解析】依题意知,a=(-1,1,3),b=(2,-3,-2),则a+b=(1,-2,1),a-2b=(-1,1,3)-2(2,-3,-2)=(-5,7,7).
14.【答案】
【解析】由,及,可知存在实数满足,即,即且且,解得.故填.
15.【答案】60°
【解析】如图,建立空间直角坐标系D-xyz,
16.【答案】①②③④
【解析】①a,b所在的直线可能重合,所以①错;
②空间任意两个向量均共面,所以②错;
③以空间向量的一组基底{a,b,c}为例,知它们两两共面,但它们三个不共面,所以③错;
④当a,b,c共面时,不成立,所以④错.
故不正确的命题为①②③④.
17.【解析】存在,理由如下:
假设a4=aa1+ba2+ca3成立,
由已知可得a1=(2,-1,1),a2=(1,3,-2),a3=(-2,1,-3),a4=(3,2,5),
可得(2a+b-2c,-a+3b+c,a-2b-3c)=(3,2,5),∴,
解得a=-2,b=1,c=-3,故a4=-2a1+a2-3a3,
所以a,b,c存在,且a=-2,b=1,c=-3.
19.【解析】如图,以D为原点,DA,DC,DD1所在直线分别为x轴、y轴、z轴建立空间直角坐标系Dxyz,设正方体的棱长为2,则,,,,,,,.
(1)易得,,
设平面的法向量为,则,即,
取,得,,
所以平面的一个法向量为.
又,所以,
所以,
显然不在平面内,所以平面.
20.【解析】如图所示,建立空间直角坐标系.
由题意易得,,,,,,
(1)由题易得,
故M,N两点之间的距离为.
(2)由题易得,.
因为,所以,即,
因为,所以,即,
又,所以平面.
(3)由题易得,
因为,所以,
所以,
故直线与所成的角为.
21.【解析】(1)由已知可得,,所以平面.
又平面,故平面平面.
(2)过作,垂足为,
由(1)知平面.
以为坐标原点,的方向为轴正方向,为单位长度,建立如图所示的空间直角坐标系.
所以,,,.
设是平面的法向量,则,
即,所以可取.
设是平面的法向量,同理可取,
所以,
易知二面角为钝角,
故二面角的余弦值为.
22.【解析】(1)设与交于,设,如图所示建立空间直角坐标系,
,
