人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题1.1 命题及其关系高二数学(理)
文档属性
| 名称 | 人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题1.1 命题及其关系高二数学(理) |

|
|
| 格式 | zip | ||
| 文件大小 | 441.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-19 00:00:00 | ||
图片预览




文档简介
知识
1.命题
一般地,在数学中,我们把用语言、符号或式子表达的,可以判断真假的_______叫做命题.其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
在本章中,我们只讨论具有“若p,则q”这种形式的命题,通常把这种形式的命题中的p叫做命题的条件,q叫做命题的结论.
注意:(1)一个数学命题要么是真命题,要么是假命题,但不能既真又假,也不能模棱两可、无法判断其真假.数学中的定义、定理、公理都是真命题.
(2)有一些语句,虽然目前还不能判断它的真假,但是随着科学技术的发展与时间的推移,总能确定它们的真假.我们把这一类语句也算作命题,如“神农架野人”,虽然目前还不能确定有没有野人,但是随着时间的推移,人们是能够考察清楚的.
(3)数学中有一些命题虽然表面上不是“若p,则q”的形式,但是把它的表述作适当改变,也可以写成“若p,则q”的形式.关键是分清命题的条件和结论.
2.四种命题
(1)原命题与逆命题
一般地,对于两个命题,如果一个命题的条件和结论分别是另一个命题的_________,那么我们把这样的两个命题叫做互逆命题.其中一个命题叫做原命题,另一个命题叫做原命题的逆命题.也就是说,如果原命题为“若p,则q”,那么它的逆命题为“若q,则p”.
(2)否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的___________,我们把这样的两个命题叫做互否命题.其中一个命题叫做原命题,另一个命题叫做原命题的否命题.也就是说,如果原命题为“若p,则q”,那么它的否命题为“若,则”.
(3)逆否命题
对于两个命题,其中一个命题的条件和结论恰好是另一个命题的__________,我们把这样的两个命题叫做互为逆否命题.如果把其中一个命题叫做原命题,那么另一个命题叫做原命题的逆否命题.
也就是说,如果原命题为“若p,则q”,那么它的逆否命题为“若,则”.
提示:在对原命题的条件和结论进行否定时,一定要注意问题的全面性,千万不能遗漏或重复.
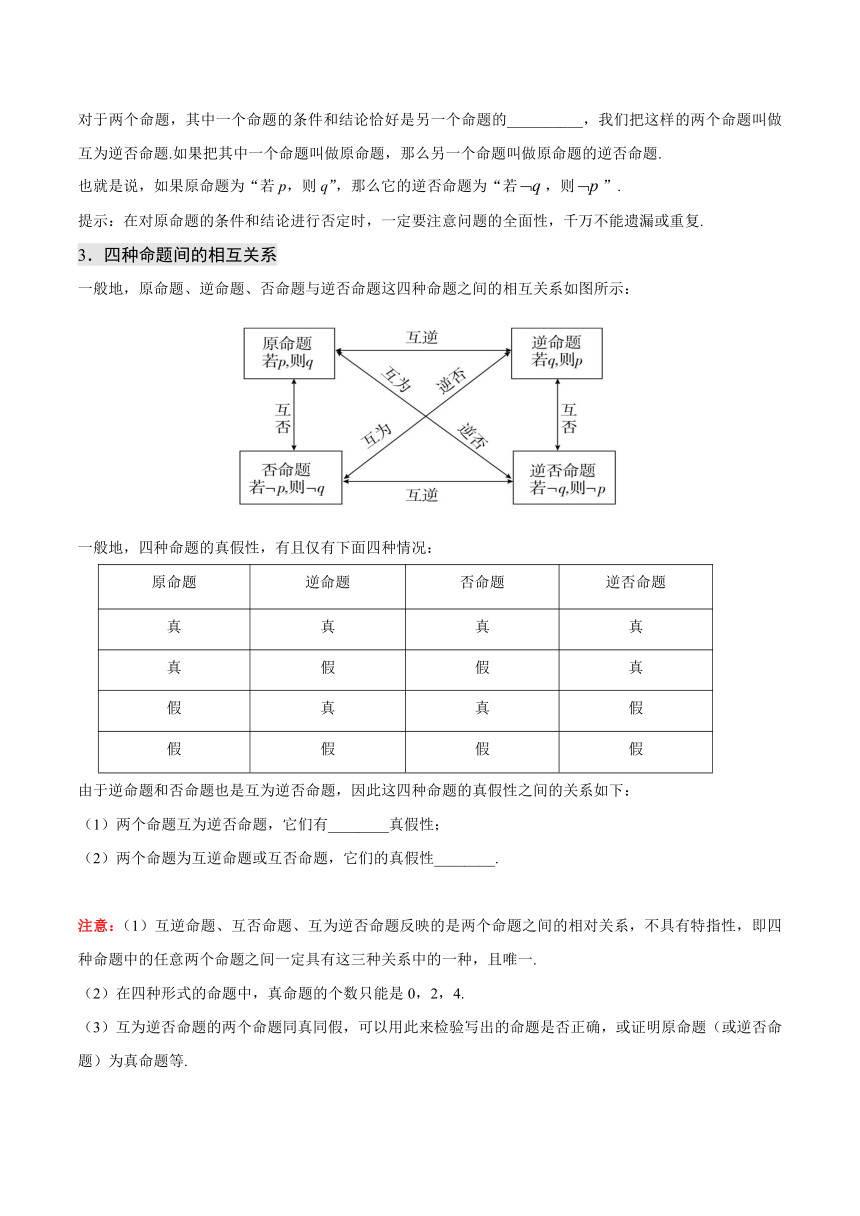
3.四种命题间的相互关系
一般地,原命题、逆命题、否命题与逆否命题这四种命题之间的相互关系如图所示:
一般地,四种命题的真假性,有且仅有下面四种情况:
原命题
逆命题
否命题
逆否命题
真
真
真
真
真
假
假
真
假
真
真
假
假
假
假
假
由于逆命题和否命题也是互为逆否命题,因此这四种命题的真假性之间的关系如下:
(1)两个命题互为逆否命题,它们有________真假性;
(2)两个命题为互逆命题或互否命题,它们的真假性________.
注意:(1)互逆命题、互否命题、互为逆否命题反映的是两个命题之间的相对关系,不具有特指性,即四种命题中的任意两个命题之间一定具有这三种关系中的一种,且唯一.
(2)在四种形式的命题中,真命题的个数只能是0,2,4.
(3)互为逆否命题的两个命题同真同假,可以用此来检验写出的命题是否正确,或证明原命题(或逆否命题)为真命题等.
知识参考答案:
1.陈述句
2.(1)结论和条件 (2)条件的否定和结论的否定 (3)结论的否定和条件的否定
3.(1)相同的 (2)没有关系
重点
重点
四种命题及其关系,命题真假的判断
难点
涉及命题真假判断的多选型试题
易错
对于含有大前提的命题,改写时,易忽略大前提
1.命题的概念及真假判断
判断一个语句是不是命题,关键看两点:第一,是否是“陈述句”;第二,是否“可以判断真假”,这两个条件缺一不可.疑问句、祈使句、感叹句均不是命题.
命题真假的判断方法:
(1)真命题的判断方法:真命题的判定过程实际就是利用命题的条件,结合正确的逻辑推理方法进行正确地逻辑推理的一个过程,判断命题为真的关键是弄清命题的条件,选择正确的逻辑推理方法.
(2)假命题的判断方法:通过构造一个反例否定命题的正确性,这是判断一个命题为假命题的常用方法.
另外,一些命题的真假也可以依据客观事实作出判断.
【例1】下列命题中的假命题是
A.在中,若,则
B.函数为奇函数
C.
D.对于任意的,直线与圆都相交
【答案】C
【例2】把下列命题改写成“若p,则q”的形式,并判断其真假.
(1)能被9整除的数是偶数;
(2)当x2+(y-1)2=0时,有x=0,y=1;
(3)如果a>1,那么函数f(x)=(a-1)x是增函数.
【解析】(1)若一个数能被9整除,则这个数是偶数.它是假命题.
(2)若x2+(y-1)2=0,则x=0,y=1.它是真命题.
(3)若a>1,则函数f(x)=(a-1)x是增函数.它是假命题.
2.四种命题
由原命题写出其他三种命题,关键要分清原命题的条件和结论.
(1)将原命题的条件和结论交换,即得原命题的逆命题.
(2)将原命题的条件和结论进行否定,作为新命题的条件和结论,即得原命题的否命题.否定命题的条件或结论,关键是否定条件或结论的关键词.
(3)先写出原命题的逆命题,再写出逆命题的否命题,即得逆否命题.也可以先写出原命题的否命题,再写出否命题的逆命题,即得逆否命题.
【例3】把下列命题改写成“若p,则q”的形式,并分别写出它们的逆命题、否命题与逆否命题,并判断真假:
①负数小于零.
②在空间中,平行于同一个平面的两条直线平行.
【解析】①原命题:若一个数是负数,则它小于零.是真命题.
逆命题:若一个数小于零,则它是负数.是真命题.
否命题:若一个数不是负数,则它不小于零.是真命题.
逆否命题:若一个数不小于零,则它不是负数.是真命题.
②原命题:在空间中,若两条直线平行于同一个平面,则这两条直线平行.是假命题.
逆命题:在空间中,若两条直线平行,则它们平行于同一个平面.是假命题.
否命题:在空间中,若两条直线不平行于同一个平面,则这两条直线不平行.是假命题.
逆否命题:在空间中,若两条直线不平行,则它们不平行于同一个平面.是假命题.
【名师点睛】对于①,“小于”的否定是“不小于”,而不是“大于”,因为“不小于”包括了“大于和等于”.
3.四种命题间的相互关系
由于原命题和它的逆否命题有相同的真假性,所以在直接证明某一个命题为真命题较困难时,可以通过证明它的逆否命题为真命题,来间接地证明原命题为真命题.
【例4】判断命题“若a>0,则x2+x-a=0有实根”的逆否命题的真假.
4.由命题的真假性求参数的值
对于此类问题,若由已知条件可以得出一个真命题,即可据此建立相应的不等式或方程求解.解题时要善于从条件中寻找解题思路,善于构造性质、定理等运用的条件.
【例5】命题:若,则;命题:若,则恒成立.若的逆命题, 的逆否命题都是真命题,则实数的取值范围是__________.
【答案】
【解析】命题的逆命题:若,则,故;
命题的逆否命题为真命题,故原命题为真命题,则,即.
故实数的取值范围是.
5.改写命题时,忽略大前提
【例6】将命题“当时,函数的值随的减小而减小”写成“若,则”的形式,并写出其逆命题、否命题和逆否命题.
【错解】“若,则”的形式:若,则函数的值随的减小而减小.
逆命题:若函数的值随的减小而减小,则.
否命题:若,则函数的值随的不减小而不减小.
逆否命题:若函数的值随的不减小而不减小,则.
?【错因分析】原命题有两个条件:和减小,其中是大前提,将原命题改写为“若,则”的形式时,要把置于“若”字的前面,把减小作为条件.
【正解】“若,则”的形式:当时,若减小,则函数的值也减小.
逆命题:当时,若函数的值减小,则也减小.
否命题:当时,若不减小,则函数的值也不减小.
逆否命题:当时,若函数的值不减小,则也不减小.
【名师点睛】(1)有大前提的命题改写成“若,则”的形式时,要注意其书写格式为“大前提,若,则”.
(2)对于含有大前提的命题,在写其他三种命题时,应保持大前提不变.
基础训练
1.命题“若,则”的逆命题是
A.若,则 B.若,则
C.若,则 D.若,则
2.下列语句中是命题的是
A.周期函数和是周期函数吗?
B.
C.
D.梯形是不是平面图形呢?
3.一个命题与它的逆命题、否命题、逆否命题这四个命题中
A.假命题与真命题的个数相同
B.真命题的个数是奇数
C.真命题的个数是偶数
D.假命题的个数是奇数
4.下列命题中为真命题的是
A.命题“若,则”的逆命题 B.命题“若,则”的否命题
C.命题“若,则”的逆否命题 D.命题“若,则”的逆命题
5.原命题:“设a,b,c∈R,若a>b,则ac2>bc2”,在原命题以及它的逆命题、否命题、逆否命题中,真命题的个数为
A.0 B.1
C.2 D.4
6.命题“若,则”的逆否命题是__________.
7.命题“若且,,则”的条件为__________,结论为__________.
8.若命题“满足”为真命题,则实数的取值范围是__________.
9.把下列命题改写成“若p,则q”的形式,并判断命题的真假.
(1)能被6整除的数一定是偶数;
(2)当时,a=1,b=-2;
(3)已知x,y为正整数,当y=x2时,y=1,x=1.
10.分别写出下列命题的逆命题、否命题和逆否命题,并判断它们的真假.
(1)若一个三角形的两条边相等,则这两条边所对的角相等;
(2)奇函数的图象关于原点对称;
(3)已知a,b,c,d是实数,若a=b,c=d,则a+c=b+d;
(4)若q<1,则方程x2+2x+q=0有实根.
能力提升
11.已知原命题“若,则、中至少有一个不小于1”,原命题与其逆命题的真假情况是
A.原命题为假,逆命题为真 B.原命题为真,逆命题为假
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
12.命题“正数a的平方根不等于0”是命题“若一个数a的平方根不等于0,则a是正数”的
A.逆命题 B.否命题
C.逆否命题 D.否定命题
13.能够说明“设是实数,若,则”是假命题的一个实数的值为________.
14.已知a,b∈R,求证:若a3+b3+3ab≠1,则a+b≠1.
15.已知两个命题,如果对任意的与有且仅有一个是真命题,求实数的取值范围.
真题练习
16.(2019山东模拟)设,命题“若,则方程有实根”的逆否命题是
A.若方程有实根,则
B.若方程有实根,则
C.若方程没有实根,则
D.若方程没有实根,则
17.(2019陕西模拟)原命题为“若,,则为递减数列”,关于逆命题,否命题,逆否命题真假性的判断依次如下,正确的是
A.真,真,真 B.假,假,真
C.真,真,假 D.假,假,假
18.(2018北京)能说明“若f(x)>f(0)对任意的x∈(0,2]都成立,则f(x)在[0,2]上是增函数”为假命题的一个函数是__________.
参考答案
1
2
3
4
5
11
12
16
17
C
B
C
D
C
B
A
D
A
1.【答案】C
【解析】因为将原命题的结论当条件,条件当结论即可到其逆命题,所以命题“若,则”的逆命题是“若,则”,故选C.
2.【答案】B
【解析】命题是可以判断真假的陈述句,4个选项中只有B满足.
3.【答案】C
【解析】一个命题与它的逆命题、否命题、逆否命题这四个命题中,真命题的个数可以为0,2,4个,所以选C.
4.【答案】D
5.【答案】C
【解析】原命题:“设a,b,c∈R,若a>b,则ac2>bc2”,当c=0时显然不成立,所以是假命题;
由于原命题是假命题,所以其逆否命题也是假命题;
逆命题为:若ac2>bc2,则a>b,是真命题;
由于逆命题和否命题互为逆否命题,所以其真假性是一样的,所以其否命题也是真命题.
所以在原命题以及它的逆命题、否命题、逆否命题中真命题的个数为2,故答案为C.
6.【答案】若,则
【解析】“若,则”的逆否命题是:若,则.
7.【答案】且,
【解析】由命题的定义易得.
8.【答案】
【解析】即,即,解得.
实数的取值范围是.
9.【解析】(1)若一个数能被6整除,则这个数为偶数.真命题.
(2)若,则且.真命题.
(3)已知,为正整数,若,则且.假命题.
10.【解析】(1)逆命题:若一个三角形的两个角相等,则这两个角所对的边相等.显然该命题是真命题.
否命题:若一个三角形的两条边不相等,则这两条边所对的角不相等.由于原命题的逆命题是真命题,所以原命题的否命题也是真命题.
逆否命题:若一个三角形的两个角不相等,则这两个角所对的边不相等.由于原命题为真命题,所以其逆否命题也是真命题.
(3)逆命题:已知a,b,c,d是实数,若a+c=b+d,则a=b,c=d.是假命题.
否命题:已知a,b,c,d是实数,若a≠b或c≠d,则a+c≠b+d.是假命题.
逆否命题:已知a,b,c,d是实数,若a+c≠b+d,则a≠b或c≠d.是真命题.
(4)逆命题:若方程x2+2x+q=0有实根,则q<1.是假命题.
否命题:若q≥1,则方程x2+2x+q=0无实根.是假命题.
逆否命题:若方程x2+2x+q=0无实根,则q≥1.是真命题.
11.【答案】B
【解析】逆否命题为:a,b都小于1,则a+b≤2,是真命题,所以原命题是真命题.
逆命题为:若、中至少有一个不小于1,则a+b>2,例如,当a=2,b=﹣2时,满足条件,此时a+b=2+(﹣2)=0,与a+b>2矛盾,故为假命题.故选B.
12.【答案】A
【解析】命题“正数的平方根不等于0”的条件为,结论为;
命题“若一个数的平方根不等于0,则是正数”的条件为,结论为.
∴命题“正数的平方根不等于0”是命题“若一个数的平方根不等于0,则是正数”的逆命题.故选A.
13.【答案】2
【解析】因为,所以,
等号成立的条件为,故当时函数值等于3.
此时不满足题干.故答案为2.
14.【解析】原命题证明较困难,故可改证它的等价命题(逆否命题):已知a,b∈R,若,则a3+b3+3ab=1.
因为,所以,
所以原命题成立.
16.【答案】D
【解析】一个命题的逆否命题,要将原命题的条件、结论加以否定,并且加以互换,故选D.
17.【答案】A
【解析】由为递减数列,所以原命题为真命题.
逆命题:若为递减数列,则,.
若为递减数列,则,即,所以逆命题为真命题.
因为逆否命题的真假和原命题的真假相同,否命题的真假和逆命题的真假相同,所以逆否命题、否命题也为真命题.故选A.
18.【答案】 (答案不唯一)
