江西省赣州市南康中学2019-2020学年高一上学期第一次大考数学试题 解析版
文档属性
| 名称 | 江西省赣州市南康中学2019-2020学年高一上学期第一次大考数学试题 解析版 |
|
|
| 格式 | zip | ||
| 文件大小 | 265.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 00:00:00 | ||
图片预览





文档简介
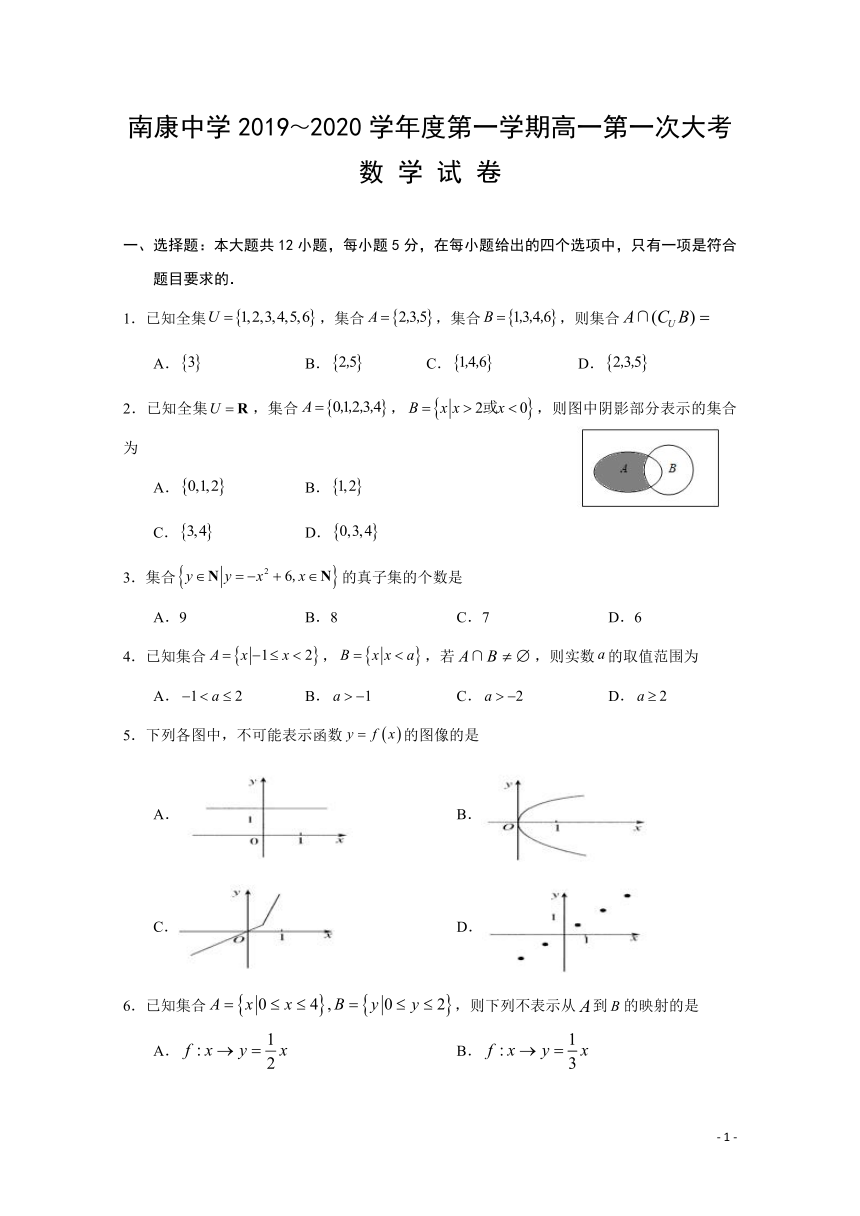
南康中学2019~2020学年度第一学期高一第一次大考
数 学 试 卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则集合
A. B. C. D.
2.已知全集,集合,,则图中阴影部分表示的集合为
A. B.
C. D.
3.集合的真子集的个数是
A.9 B.8 C.7 D.6
4.已知集合,,若,则实数的取值范围为
A. B. C. D.
5.下列各图中,不可能表示函数的图像的是
A. B.
C. D.
6.已知集合,则下列不表示从到的映射的是
A. B.
C. D.
7.下列四组函数中,表示相同函数的一组是
A. B.
C. D.
8.设函数,若,则
A.或 B.或 C.或 D.或或
9.下列函数中,不满足:是
A. B. C. D.
10.已知集合,,则能使成立的实数的取值范围是
A. B. C. D.
11.若函数的定义域、值域都是则
A. B. C. D.
12.对任意实数x,规定f(x)取4-x,x+1,(5-x)三个值中的最小值,则f(x)
A.无最大值,无最小值 B.有最大值2,最小值1
C.有最大值1,无最小值 D.有最大值2,无最小值
二、填空题:本大题共4小题,每小题5分.
13.若,,则_____ ______.
14.已知,则______ _____.
15.已知f(x)=则f(3)的值为__ ______.
16.已知函数满足,且,,
那么____ _.(用,表示)
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
若,集合,
求:(1);
(2).
18.(12分)
已知集合,,且.
(1)用反证法证明;
(2)若,求实数的值.
19.(12分)
已知方程的两个不相等实根为.集合,,
,且.
求实数的值.
20.(12分)
已知二次函数满足,试求:
(1)求的解析式;
(2)若,试求函数的值域.
21.(12分)
某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是
p=该商品的日销售量Q(件)与时间t(天)的函数关系是
Q=-t+40(022.(12分)
已知函数.
(1)直接写出此函数的定义域与值域(用区间表示);
(2)证明:对于任意的,都有 ;
(3)用单调性定义证明在上是减函数.
南康中学2019~2020学年度第一学期高一第一次大考
数学试卷参考答案
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】∵,,∴,
∵,则,故选B.
2.【答案】A
【解析】∵全集,集合,,∴,
∴图中阴影部分表示的集合为,故选A.
3.【答案】C
【解析】时,;时,;时,;时,;
∵函数在上是减函数,
∴当时,;,共3个元素,
可得其真子集的个数为个,故选C.
4.【答案】B
【解析】∵,,,
作出图形如下:
∴,故选B.
5.【答案】B
【解析】函数表示每个自变量有唯一的函数值与之对应的一种对应关系,
对B中图象,的值,有两个值与之对应,故不是函数图象,故选B.
6.【答案】C
【解析】对于选项,集合中每一个值,
集合中都存在唯一的与之对应,因此符合映射“都有像,
像唯一”的定义;
对于选项C,当时,B中不存在元素与之对应即当时“无像”,
所以不是从到的映射,故选C.
7.【答案】A
【解析】∵只有当定义域和对应法则相同的时候,才能保证函数相同
可知选项B、C、D中,定义域不同.∴只能选A.
8.【答案】C
【解析】当时,由,可得,符合题意;
当时,由,可得或(舍),
综上可知,的值是或,故选C.
9.【答案】D
【解析】A中;
B中;
C中;
D中.
10.【答案】C
【解析】∵,∴,∴,故选C.
11.【答案】A
【解析】∵函数的对称轴为,
由二次函数的性质可得在上为增函数,且有,
∵函数的定义域,值域都是,,
即,
化简可得,解得或(舍去),故选A.
12.【答案】D [画出f(x)的图像,如图,由得A(1,2).]
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】,,∴.
14.【答案】
【解析】令,
那么,则,故答案为.
15.【答案】2 [f(3)=f(7)=7-5=2.]
16.【答案】
【解析】因为满足,且,,
所以,所以,故填.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【解】(1)∵是分母,∴,因此只能;………………5分
(2)由得,即
∴,
∴.………………10分
18.【解】(1)由,解得或,,
设,则必有,与矛盾,∴假设错误,
∴;………………6分
(2)∵又∴,又,∴可能为,
当或时,要求,即,
①当时,适合;
②当时=不适合,应舍去.
综上,实数.………………12分
19.【解】由,知,
又,则,,而,故,,
显然即属于又不属于的元素只有1和3.
不妨设,………………6分
对于方程的两根,
应用韦达定理可得,.………………12分
20.【解】(1)设,
则有,对任意实数恒成立,
,解之得,,,.…………6分
(2)由(1)可得在上递减,在递增,
又,,
∴函数的值域为.………………12分
21.【解】∵日销售金额y=p·Q,
∴ y=………………6分
=
当0当25≤t≤30,t∈N,t=25时.ymax=1125(元)
∵ 1125>900,∴第25天日销售金额最大,ymax=1125(元).…………12分
答:略
22【解】(1)定义域,值域……………………4分
(2)对于任意的,…………8分
(3)令
∵
又∵,∴,
∴即
∴在上是减函数.……………………12分
数 学 试 卷
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知全集,集合,集合,则集合
A. B. C. D.
2.已知全集,集合,,则图中阴影部分表示的集合为
A. B.
C. D.
3.集合的真子集的个数是
A.9 B.8 C.7 D.6
4.已知集合,,若,则实数的取值范围为
A. B. C. D.
5.下列各图中,不可能表示函数的图像的是
A. B.
C. D.
6.已知集合,则下列不表示从到的映射的是
A. B.
C. D.
7.下列四组函数中,表示相同函数的一组是
A. B.
C. D.
8.设函数,若,则
A.或 B.或 C.或 D.或或
9.下列函数中,不满足:是
A. B. C. D.
10.已知集合,,则能使成立的实数的取值范围是
A. B. C. D.
11.若函数的定义域、值域都是则
A. B. C. D.
12.对任意实数x,规定f(x)取4-x,x+1,(5-x)三个值中的最小值,则f(x)
A.无最大值,无最小值 B.有最大值2,最小值1
C.有最大值1,无最小值 D.有最大值2,无最小值
二、填空题:本大题共4小题,每小题5分.
13.若,,则_____ ______.
14.已知,则______ _____.
15.已知f(x)=则f(3)的值为__ ______.
16.已知函数满足,且,,
那么____ _.(用,表示)
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.(10分)
若,集合,
求:(1);
(2).
18.(12分)
已知集合,,且.
(1)用反证法证明;
(2)若,求实数的值.
19.(12分)
已知方程的两个不相等实根为.集合,,
,且.
求实数的值.
20.(12分)
已知二次函数满足,试求:
(1)求的解析式;
(2)若,试求函数的值域.
21.(12分)
某商品在近30天内每件的销售价格p(元)与时间t(天)的函数关系是
p=该商品的日销售量Q(件)与时间t(天)的函数关系是
Q=-t+40(0
已知函数.
(1)直接写出此函数的定义域与值域(用区间表示);
(2)证明:对于任意的,都有 ;
(3)用单调性定义证明在上是减函数.
南康中学2019~2020学年度第一学期高一第一次大考
数学试卷参考答案
一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.【答案】B
【解析】∵,,∴,
∵,则,故选B.
2.【答案】A
【解析】∵全集,集合,,∴,
∴图中阴影部分表示的集合为,故选A.
3.【答案】C
【解析】时,;时,;时,;时,;
∵函数在上是减函数,
∴当时,;,共3个元素,
可得其真子集的个数为个,故选C.
4.【答案】B
【解析】∵,,,
作出图形如下:
∴,故选B.
5.【答案】B
【解析】函数表示每个自变量有唯一的函数值与之对应的一种对应关系,
对B中图象,的值,有两个值与之对应,故不是函数图象,故选B.
6.【答案】C
【解析】对于选项,集合中每一个值,
集合中都存在唯一的与之对应,因此符合映射“都有像,
像唯一”的定义;
对于选项C,当时,B中不存在元素与之对应即当时“无像”,
所以不是从到的映射,故选C.
7.【答案】A
【解析】∵只有当定义域和对应法则相同的时候,才能保证函数相同
可知选项B、C、D中,定义域不同.∴只能选A.
8.【答案】C
【解析】当时,由,可得,符合题意;
当时,由,可得或(舍),
综上可知,的值是或,故选C.
9.【答案】D
【解析】A中;
B中;
C中;
D中.
10.【答案】C
【解析】∵,∴,∴,故选C.
11.【答案】A
【解析】∵函数的对称轴为,
由二次函数的性质可得在上为增函数,且有,
∵函数的定义域,值域都是,,
即,
化简可得,解得或(舍去),故选A.
12.【答案】D [画出f(x)的图像,如图,由得A(1,2).]
二、填空题:本大题共4小题,每小题5分.
13.【答案】
【解析】,,∴.
14.【答案】
【解析】令,
那么,则,故答案为.
15.【答案】2 [f(3)=f(7)=7-5=2.]
16.【答案】
【解析】因为满足,且,,
所以,所以,故填.
三、解答题:本大题共6个大题,共70分,解答应写出文字说明、证明过程或演算步骤.
17.【解】(1)∵是分母,∴,因此只能;………………5分
(2)由得,即
∴,
∴.………………10分
18.【解】(1)由,解得或,,
设,则必有,与矛盾,∴假设错误,
∴;………………6分
(2)∵又∴,又,∴可能为,
当或时,要求,即,
①当时,适合;
②当时=不适合,应舍去.
综上,实数.………………12分
19.【解】由,知,
又,则,,而,故,,
显然即属于又不属于的元素只有1和3.
不妨设,………………6分
对于方程的两根,
应用韦达定理可得,.………………12分
20.【解】(1)设,
则有,对任意实数恒成立,
,解之得,,,.…………6分
(2)由(1)可得在上递减,在递增,
又,,
∴函数的值域为.………………12分
21.【解】∵日销售金额y=p·Q,
∴ y=………………6分
=
当0
∵ 1125>900,∴第25天日销售金额最大,ymax=1125(元).…………12分
答:略
22【解】(1)定义域,值域……………………4分
(2)对于任意的,…………8分
(3)令
∵
又∵,∴,
∴即
∴在上是减函数.……………………12分
同课章节目录
