青岛版九年级数学上册第1章 图形的相似1.2 怎样判定三角形相似(2)同步练习附答案解析
文档属性
| 名称 | 青岛版九年级数学上册第1章 图形的相似1.2 怎样判定三角形相似(2)同步练习附答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 58.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 11:58:46 | ||
图片预览

文档简介
1.2 怎样判定三角形相似(2)
1.下列说法错误的是( )
A.有一个角是30°的两个等腰三角形相似
B.有一个角是60°的两个等腰三角形相似
C.有一个角是90°的两个等腰三角形相似
D.有一个角是120°的两个等腰三角形相似
2.已知△MNP如图所示,则下列四个三角形中与△MNP相似的是( )
(第2题)
3. 如图,矩形ABCG(ABA. 0个 B. 1个 C. 2个 D. 3个
(第3题) (第4题)
4.如图,△ABC中,D,E分别是AB,AC上的点,有下列条件:①∠AED=∠B;②=;③=.其中能够判断△ADE与△ACB相似的有( )
A.①② B.①③
C.①②③ D.①
5.在△ABC中,E是AB上一点,AE=2,BE=3,AC=4.在AC上取一点D,使△ADE与△ABC相似,则AD的值是( )
A. B. C.或 D.或
6.如图,BC平分∠ABD,AB=4,BD=6,当BC= 时,△ABC∽△CBD.
(第6题)
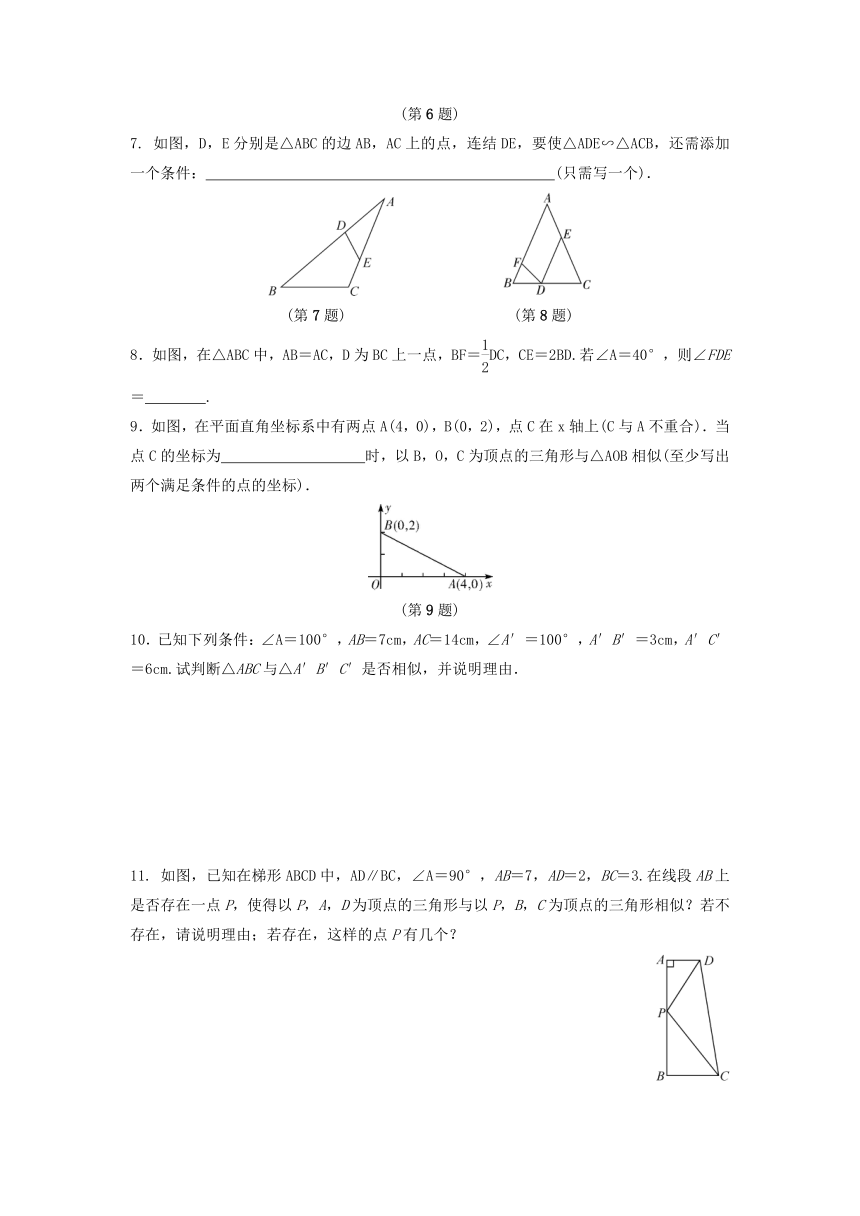
7. 如图,D,E分别是△ABC的边AB,AC上的点,连结DE,要使△ADE∽△ACB,还需添加一个条件: (只需写一个).
(第7题) (第8题)
8.如图,在△ABC中,AB=AC,D为BC上一点,BF=DC,CE=2BD.若∠A=40°,则∠FDE= .
9.如图,在平面直角坐标系中有两点A(4,0),B(0,2),点C在x轴上(C与A不重合).当点C的坐标为 时,以B,O,C为顶点的三角形与△AOB相似(至少写出两个满足条件的点的坐标).
(第9题)
10.已知下列条件:∠A=100°,AB=7cm,AC=14cm,∠A′=100°,A′B′=3cm,A′C′=6cm.试判断△ABC与△A′B′C′是否相似,并说明理由.
11. 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3.在线段AB上是否存在一点P,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若不存在,请说明理由;若存在,这样的点P有几个?
(第11题)
12. 如图,在△ABC中,AB=6,BC=4,AC=3.点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D,设PB=x,AD=y.
(1)求y关于x的函数表达式和自变量x的取值范围;
(2)当x取何值时,y最小?最小值是多少?
(第12题)
13.如图,已知BD∥AC,AB=3AC,BD=3AE,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE;
(2)若AC=BD,AD=2 BD,设BD=a,求BC的长.
(第13题)
参考答案
1.A 2.C 3. C 4.A
5.C 【解析】 如解图.(1)当△ADE∽△ABC时,有=.∵AE=2,BE=3,∴AB=5.∴=,∴AD=.(2)当△AED∽△ABC时,有=,∴=,∴AD=.
(第5题解)
6. 2
7. 此题答案不唯一,如∠ADE=∠C或∠AED=∠B或AD·AB=AE·AC或AD∶AC=AE∶AB等
8.70°
9. (1,0)或(-1,0)或(-4,0)
10.【解】 相似,理由如下:
∵=,==,
∴=.
又∵∠A=∠A′=100°,
∴△ABC∽△A′B′C′.
11. 【解】 存在点P,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似,这样的点P有3个.理由如下:
要使△PAD和△PBC相似,因为∠A=∠B=90°,根据两边成比例,夹角相等的两个三角形相似,应有=或=.
设AP=x(0代入已知数据,可得=或=,
解得x1=2.8,x2=1,x3=6.
∴PA=1或2.8或6.
即这样的点P共有3个.
12. 【解】 (1)∵∠B=∠B,∠DPB=∠A,
∴△BPD∽△BAC,
∴=,即=,
∴y=6-x(0<x≤4).
(2)当x=4时,y最小,最小值是.
13.【解】 (1)∵BD∥AC,且点B,A,E在同一条直线上,
∴∠DBA=∠CAE.
又∵==3,
∴△ABD∽△CAE.
(2)∵AB=3AC,AC=BD,AD=2 BD,
∴AB=3BD,∴AB2=(3BD)2=9BD2,AD2+BD2=8BD2+BD2=9BD2,
∴AB2=AD2+BD2,∴∠D=90°.
由(1)得△ABD∽△CAE,
∴∠E=∠D=90°,EC=AD= BD.
在Rt△BCE中,
∵AE=BD,AB=3BD,
∴BC2=BE2+EC2=(AB+AE)2+EC2
=+
=12BD2=12a2,
∴BC=2 a.
1.下列说法错误的是( )
A.有一个角是30°的两个等腰三角形相似
B.有一个角是60°的两个等腰三角形相似
C.有一个角是90°的两个等腰三角形相似
D.有一个角是120°的两个等腰三角形相似
2.已知△MNP如图所示,则下列四个三角形中与△MNP相似的是( )
(第2题)
3. 如图,矩形ABCG(AB
(第3题) (第4题)
4.如图,△ABC中,D,E分别是AB,AC上的点,有下列条件:①∠AED=∠B;②=;③=.其中能够判断△ADE与△ACB相似的有( )
A.①② B.①③
C.①②③ D.①
5.在△ABC中,E是AB上一点,AE=2,BE=3,AC=4.在AC上取一点D,使△ADE与△ABC相似,则AD的值是( )
A. B. C.或 D.或
6.如图,BC平分∠ABD,AB=4,BD=6,当BC= 时,△ABC∽△CBD.
(第6题)
7. 如图,D,E分别是△ABC的边AB,AC上的点,连结DE,要使△ADE∽△ACB,还需添加一个条件: (只需写一个).
(第7题) (第8题)
8.如图,在△ABC中,AB=AC,D为BC上一点,BF=DC,CE=2BD.若∠A=40°,则∠FDE= .
9.如图,在平面直角坐标系中有两点A(4,0),B(0,2),点C在x轴上(C与A不重合).当点C的坐标为 时,以B,O,C为顶点的三角形与△AOB相似(至少写出两个满足条件的点的坐标).
(第9题)
10.已知下列条件:∠A=100°,AB=7cm,AC=14cm,∠A′=100°,A′B′=3cm,A′C′=6cm.试判断△ABC与△A′B′C′是否相似,并说明理由.
11. 如图,已知在梯形ABCD中,AD∥BC,∠A=90°,AB=7,AD=2,BC=3.在线段AB上是否存在一点P,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似?若不存在,请说明理由;若存在,这样的点P有几个?
(第11题)
12. 如图,在△ABC中,AB=6,BC=4,AC=3.点P在边BC上运动(不含点B),过点P作∠DPB=∠A,PD交AB于点D,设PB=x,AD=y.
(1)求y关于x的函数表达式和自变量x的取值范围;
(2)当x取何值时,y最小?最小值是多少?
(第12题)
13.如图,已知BD∥AC,AB=3AC,BD=3AE,点B,A,E在同一条直线上.
(1)求证:△ABD∽△CAE;
(2)若AC=BD,AD=2 BD,设BD=a,求BC的长.
(第13题)
参考答案
1.A 2.C 3. C 4.A
5.C 【解析】 如解图.(1)当△ADE∽△ABC时,有=.∵AE=2,BE=3,∴AB=5.∴=,∴AD=.(2)当△AED∽△ABC时,有=,∴=,∴AD=.
(第5题解)
6. 2
7. 此题答案不唯一,如∠ADE=∠C或∠AED=∠B或AD·AB=AE·AC或AD∶AC=AE∶AB等
8.70°
9. (1,0)或(-1,0)或(-4,0)
10.【解】 相似,理由如下:
∵=,==,
∴=.
又∵∠A=∠A′=100°,
∴△ABC∽△A′B′C′.
11. 【解】 存在点P,使得以P,A,D为顶点的三角形与以P,B,C为顶点的三角形相似,这样的点P有3个.理由如下:
要使△PAD和△PBC相似,因为∠A=∠B=90°,根据两边成比例,夹角相等的两个三角形相似,应有=或=.
设AP=x(0
解得x1=2.8,x2=1,x3=6.
∴PA=1或2.8或6.
即这样的点P共有3个.
12. 【解】 (1)∵∠B=∠B,∠DPB=∠A,
∴△BPD∽△BAC,
∴=,即=,
∴y=6-x(0<x≤4).
(2)当x=4时,y最小,最小值是.
13.【解】 (1)∵BD∥AC,且点B,A,E在同一条直线上,
∴∠DBA=∠CAE.
又∵==3,
∴△ABD∽△CAE.
(2)∵AB=3AC,AC=BD,AD=2 BD,
∴AB=3BD,∴AB2=(3BD)2=9BD2,AD2+BD2=8BD2+BD2=9BD2,
∴AB2=AD2+BD2,∴∠D=90°.
由(1)得△ABD∽△CAE,
∴∠E=∠D=90°,EC=AD= BD.
在Rt△BCE中,
∵AE=BD,AB=3BD,
∴BC2=BE2+EC2=(AB+AE)2+EC2
=+
=12BD2=12a2,
∴BC=2 a.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
