青岛版九年级数学上册第2章 解直角三角形2.4 解直角三角形同步练习附答案解析
文档属性
| 名称 | 青岛版九年级数学上册第2章 解直角三角形2.4 解直角三角形同步练习附答案解析 |  | |
| 格式 | zip | ||
| 文件大小 | 168.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 12:17:50 | ||
图片预览



文档简介
2.4 解直角三角形
1.菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的个数有( )
①DE=3cm; ②BE=1cm; ③菱形的面积为15cm2; ④BD=2cm.
第1题图
A.1个 B.2个 C.3个 D.4个
2.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=, 则下列结论中正确的个数为( ) ①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
第2题图
A.3个 B.2个 C.1个 D.0个
3.如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=, 则点P的坐标是(??? ?)
第3题图
A.(2,3) B.(2,) C.(, 2) D.(2,)
4.如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
第4题图
A.2 B.4 C.8 D.8
5.如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(?? )
第5题图
A.10米 B.15米 C.25米 D.30米
6.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
第6题图
A.(4.8,6.4) B.(4,6) C.(5.4,5.8) D.(5,6)
7.如图,在梯形ABCD中,AD∥BC,BD⊥DC,∠C=60°,AD=4,BC=6,则AB长为( )
第7题图
A.2 B. C.5 D.
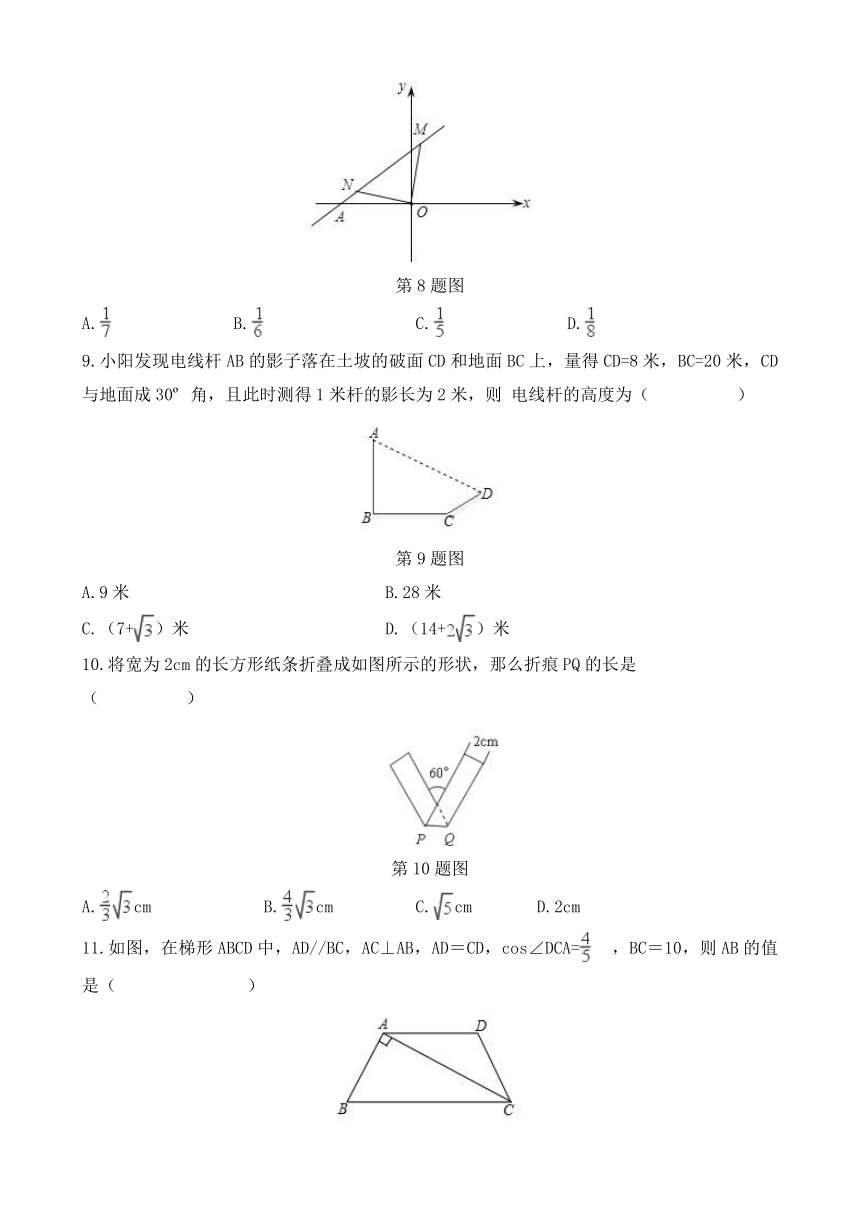
8.如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M.N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为(?? )??????????
第8题图
A. B. C. D.
9.小阳发现电线杆AB的影子落在土坡的破面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30o 角,且此时测得1米杆的影长为2米,则 电线杆的高度为( ? ? ? )
第9题图
A.9米 B.28米 C.(7+)米 D.(14+)米
10.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( ? ? ? )????
第10题图
A.cm B.cm C.cm D.2cm
11.如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA=?,BC=10,则AB的值是(??????? )
第11题图
A.3 B.6 C.8 D.9
12.如图,在△ABC中,∠BAC=90°,AD⊥BC于D , DC=4,BC=9,则AC为( )
第12题图
A.5 B.6 C.7 D.8
13.在△ABC中,∠A,∠B均为锐角,且sinA=, cosB=, AC=40,则△ABC的面积是( )
A.800 B.800 C.400 D.400
14.如图,AB是⊙O的直径,C.D是圆上的两点.若BC=8,cosD=, 则AB的长为( )
第14题图
A. B. C. D.12
15.一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( ? ?? )
第15题图
A.75cm2 B.(25+25)cm2 C.(25+)cm2 D.(25+)cm2
16.在Rt△ABC中,∠A=90°,AB=2,若sinC=, 则BC的长度为________?
17.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=, 则cos∠ADC=________.
第17题图 第18题图
18.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=, 则AD的长为________.
19.如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
第19题图 第20题图
20.如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm.BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________
21.如图,矩形ABCD的对角线AC.BD相交于点O , 过点O作OE⊥AC交AD于E , 若AB=6,AD=8,求sin∠OEA的值 .
?
第21题图
22.如图,AD是△ABC的中线,tanB=, cosC=, AC=. 求:
(1)BC的长;
(2)sin∠ADC的值.
第22题图
23.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
第23题图
24.如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于E,AE=1.求梯形ABCD的高.
?
第24题图
25.已知,如图,△ABC中.AD⊥BC于D,AC=10,BC=21,△ABC面积为84,求sinBcosC+cosBsinC的值.
第25题图
答案部分
1. C 2. A 3. D 4. B 5. B 6. A 7. B
8. A 9. D 10. B 11. B 12. B 13. D 14. D
15. C 16. 10
17. 18. 2 19. 20.
21.【解】连接EC , 如答图
第21题答图
∵四边形ABCD为矩形, ∴OA=OC , ∠ABC=90°, 利用勾股定理得:AC= =10,即OA=5, ∵OE⊥AC , ∴AE=CE , 在Rt△EDC中,设EC=AE=x , 则有ED=AD-AE=8-x , DC=AB=6, 根据勾股定理得:x2=(8-x)2+62, 解得:x= , ∴AE= , 在Rt△AOE中,sin∠OEA= . ?
22.【解】(1)过点A作AE⊥BC于点E,如答图. ∵cosC=,∴∠C=45°, 在Rt△ACE中,CE=AC?cosC=1, ∴AE=CE=1, 在Rt△ABE中,tanB=,即=, ∴BE=3AE=3, ∴BC=BE+CE=4; (2)∵AD是△ABC的中线, ∴CD=BC=2, ∴DE=CD﹣CE=1, ∵AE⊥BC,DE=AE, ∴∠ADC=45°, ∴sin∠ADC=.
第22题答图
23.【解】(1)∵DE⊥AB, ∴∠DEA=90°, ∴∠A+∠ADE=90°, ∵∠ACB=90°, ∴∠A+∠B=90°, ∴∠ADE=∠B, 在Rt△ABC中,∵AC=12,BC=5, ∴AB=13, ∴, ∴; (2)由(1)得, 设AD为x,则, ∵AC=AD+CD=12, ∴, 解得, ∴. 24.【解】∵AD∥BC,∴∠2=∠3 又AB=AD,∴∠1=∠3∠ABC=∠C=60° ∴∠1=∠2=30° 在Rt△ABE中,AE=1,∠1=30°, ∴AB=2 作AF⊥BC垂足为F,如答图. 在Rt△ABF中,AF=AB?sin∠ABC=AB?sin60°=2×= ∴梯形ABCD的高为.
?
第24题答图
25.【解】∵AD⊥BC,S△ABC=84,BC=21, ∴BC?AD=84,即×21×AD=84,解得,AD=8??????????????????????? ∵AC=10, ∴在直角△ACD中,由勾股定理得到:CD==6 ∴在直角△ABD中,BD=15,AB==17??????????????? ∴sinB==,cosB==,sinC==,cosC== ∴sinBcosC+cosBsinC=×+×=.
1.菱形ABCD的周长为20cm,DE⊥AB,垂足为E,sinA=,则下列结论正确的个数有( )
①DE=3cm; ②BE=1cm; ③菱形的面积为15cm2; ④BD=2cm.
第1题图
A.1个 B.2个 C.3个 D.4个
2.如图,菱形ABCD的周长为20cm,DE⊥AB,垂足为E,cosA=, 则下列结论中正确的个数为( ) ①DE=3cm;②EB=1cm;③S菱形ABCD=15cm2
第2题图
A.3个 B.2个 C.1个 D.0个
3.如图,在直角坐标平面内,点P与原点O的距离OP=3,线段OP与X轴正半轴的夹角为a,且cosα=, 则点P的坐标是(??? ?)
第3题图
A.(2,3) B.(2,) C.(, 2) D.(2,)
4.如图,在菱形ABCD中,∠ABC=60°,AC=4,则BD的长为( )
第4题图
A.2 B.4 C.8 D.8
5.如图,一棵大树在一次强台风中于离地面5米处折断倒下,倒下部分与地面成30°夹角,这棵大树在折断前的高度为(?? )
第5题图
A.10米 B.15米 C.25米 D.30米
6.如图,在直角坐标系中,将矩形OABC沿OB对折,使点A落在点A1处,已知OA=8,OC=4,则点A1的坐标为( )
第6题图
A.(4.8,6.4) B.(4,6) C.(5.4,5.8) D.(5,6)
7.如图,在梯形ABCD中,AD∥BC,BD⊥DC,∠C=60°,AD=4,BC=6,则AB长为( )
第7题图
A.2 B. C.5 D.
8.如图,直线y=x+3交x轴于A点,将一块等腰直角三角形纸板的直角顶点置于原点O,另两个顶点M.N恰落在直线y=x+3上,若N点在第二象限内,则tan∠AON的值为(?? )??????????
第8题图
A. B. C. D.
9.小阳发现电线杆AB的影子落在土坡的破面CD和地面BC上,量得CD=8米,BC=20米,CD与地面成30o 角,且此时测得1米杆的影长为2米,则 电线杆的高度为( ? ? ? )
第9题图
A.9米 B.28米 C.(7+)米 D.(14+)米
10.将宽为2cm的长方形纸条折叠成如图所示的形状,那么折痕PQ的长是( ? ? ? )????
第10题图
A.cm B.cm C.cm D.2cm
11.如图,在梯形ABCD中,AD//BC,AC⊥AB,AD=CD,cos∠DCA=?,BC=10,则AB的值是(??????? )
第11题图
A.3 B.6 C.8 D.9
12.如图,在△ABC中,∠BAC=90°,AD⊥BC于D , DC=4,BC=9,则AC为( )
第12题图
A.5 B.6 C.7 D.8
13.在△ABC中,∠A,∠B均为锐角,且sinA=, cosB=, AC=40,则△ABC的面积是( )
A.800 B.800 C.400 D.400
14.如图,AB是⊙O的直径,C.D是圆上的两点.若BC=8,cosD=, 则AB的长为( )
第14题图
A. B. C. D.12
15.一副三角板按图1所示的位置摆放.将△DEF绕点A(F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( ? ?? )
第15题图
A.75cm2 B.(25+25)cm2 C.(25+)cm2 D.(25+)cm2
16.在Rt△ABC中,∠A=90°,AB=2,若sinC=, 则BC的长度为________?
17.如图所示,四边形ABCD中,∠B=90°,AB=2,CD=8,AC⊥CD,若sin∠ACB=, 则cos∠ADC=________.
第17题图 第18题图
18.如图,在等腰Rt△ABC中,∠C=90°,AC=6,D是AC上一点,若tan∠DBA=, 则AD的长为________.
19.如图,在正方形ABCD外作等腰直角△CDE,DE=CE,连接BE,则tan∠EBC=________.
第19题图 第20题图
20.如图,△ABC是一张直角三角形纸片,∠C=90°,两直角边AC=6cm.BC=8cm,现将△ABC折叠,使点B与点A重合,折痕为EF,则tan∠CAE=________
21.如图,矩形ABCD的对角线AC.BD相交于点O , 过点O作OE⊥AC交AD于E , 若AB=6,AD=8,求sin∠OEA的值 .
?
第21题图
22.如图,AD是△ABC的中线,tanB=, cosC=, AC=. 求:
(1)BC的长;
(2)sin∠ADC的值.
第22题图
23.如图,在△ABC中,∠ACB=90°,D为AC上一点,DE⊥AB于点E,AC=12,BC=5.
(1)求cos∠ADE的值;
(2)当DE=DC时,求AD的长.
第23题图
24.如图,在梯形ABCD中,AD∥BC,AB=DC=AD,∠C=60°,AE⊥BD于E,AE=1.求梯形ABCD的高.
?
第24题图
25.已知,如图,△ABC中.AD⊥BC于D,AC=10,BC=21,△ABC面积为84,求sinBcosC+cosBsinC的值.
第25题图
答案部分
1. C 2. A 3. D 4. B 5. B 6. A 7. B
8. A 9. D 10. B 11. B 12. B 13. D 14. D
15. C 16. 10
17. 18. 2 19. 20.
21.【解】连接EC , 如答图
第21题答图
∵四边形ABCD为矩形, ∴OA=OC , ∠ABC=90°, 利用勾股定理得:AC= =10,即OA=5, ∵OE⊥AC , ∴AE=CE , 在Rt△EDC中,设EC=AE=x , 则有ED=AD-AE=8-x , DC=AB=6, 根据勾股定理得:x2=(8-x)2+62, 解得:x= , ∴AE= , 在Rt△AOE中,sin∠OEA= . ?
22.【解】(1)过点A作AE⊥BC于点E,如答图. ∵cosC=,∴∠C=45°, 在Rt△ACE中,CE=AC?cosC=1, ∴AE=CE=1, 在Rt△ABE中,tanB=,即=, ∴BE=3AE=3, ∴BC=BE+CE=4; (2)∵AD是△ABC的中线, ∴CD=BC=2, ∴DE=CD﹣CE=1, ∵AE⊥BC,DE=AE, ∴∠ADC=45°, ∴sin∠ADC=.
第22题答图
23.【解】(1)∵DE⊥AB, ∴∠DEA=90°, ∴∠A+∠ADE=90°, ∵∠ACB=90°, ∴∠A+∠B=90°, ∴∠ADE=∠B, 在Rt△ABC中,∵AC=12,BC=5, ∴AB=13, ∴, ∴; (2)由(1)得, 设AD为x,则, ∵AC=AD+CD=12, ∴, 解得, ∴. 24.【解】∵AD∥BC,∴∠2=∠3 又AB=AD,∴∠1=∠3∠ABC=∠C=60° ∴∠1=∠2=30° 在Rt△ABE中,AE=1,∠1=30°, ∴AB=2 作AF⊥BC垂足为F,如答图. 在Rt△ABF中,AF=AB?sin∠ABC=AB?sin60°=2×= ∴梯形ABCD的高为.
?
第24题答图
25.【解】∵AD⊥BC,S△ABC=84,BC=21, ∴BC?AD=84,即×21×AD=84,解得,AD=8??????????????????????? ∵AC=10, ∴在直角△ACD中,由勾股定理得到:CD==6 ∴在直角△ABD中,BD=15,AB==17??????????????? ∴sinB==,cosB==,sinC==,cosC== ∴sinBcosC+cosBsinC=×+×=.
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
