人教版数学七年级下册《 5.2.2 平行线的判定》 课件(22张PPT)
文档属性
| 名称 | 人教版数学七年级下册《 5.2.2 平行线的判定》 课件(22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 578.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 20:23:57 | ||
图片预览




文档简介
(共22张PPT)
5.2.2 平行线的判定
1、在同一平面内,两直线的位置关系有__________
相交和平行
2、平行公理:
经过直线外一点, 一条直线与这条直线平行。
有且只有
3、思考:
我们该怎样画出过直线外一点与这条直线平行
的直线呢?
温故知新
1
2
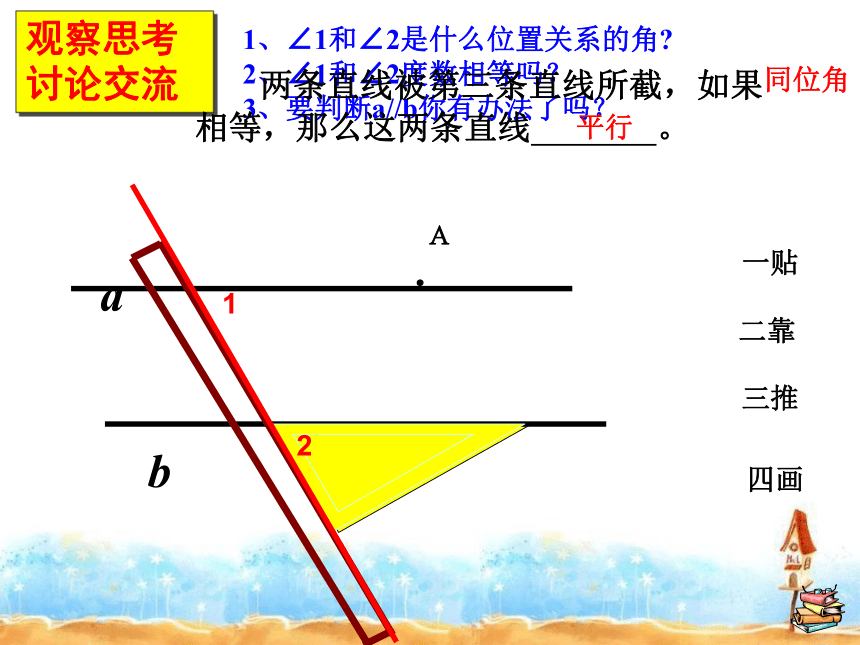
观察思考
讨论交流
a
b
.
A
1、∠1和∠2是什么位置关系的角?
2、∠1和∠2度数相等吗?
3、要判断a//b你有办法了吗?
一贴
二靠
三推
四画
两条直线被第三条直线所截,如果
相等,那么这两条直线 。
同位角
平行
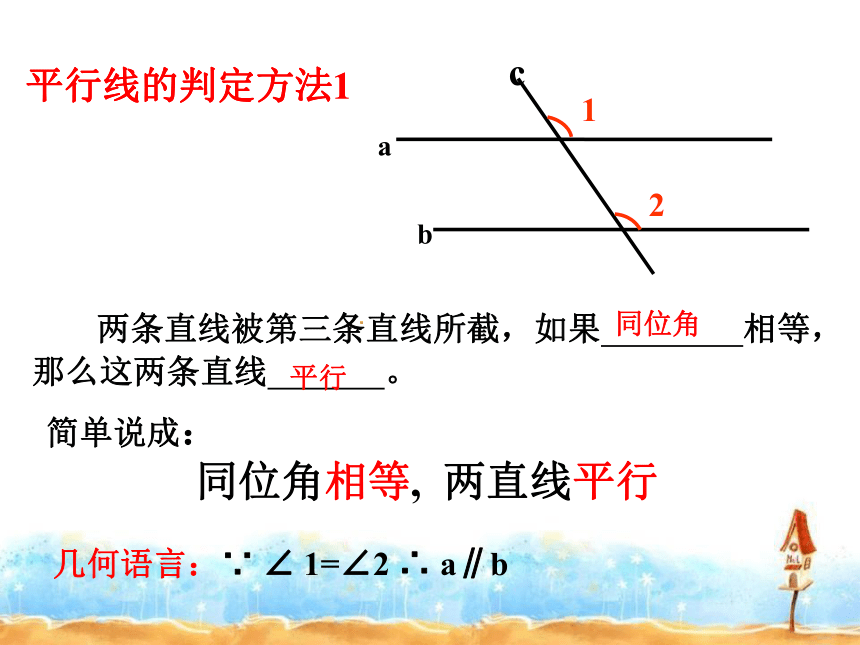
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行
平行线的判定方法1
同位角
平行
平行线的判定方法1
1、如图所示,已知∠1=60°,
当∠2=___°时,a∥b。
2、如图所示,已知∠1=60°,
当∠3=___°时,a∥b。
小试牛刀
60
120
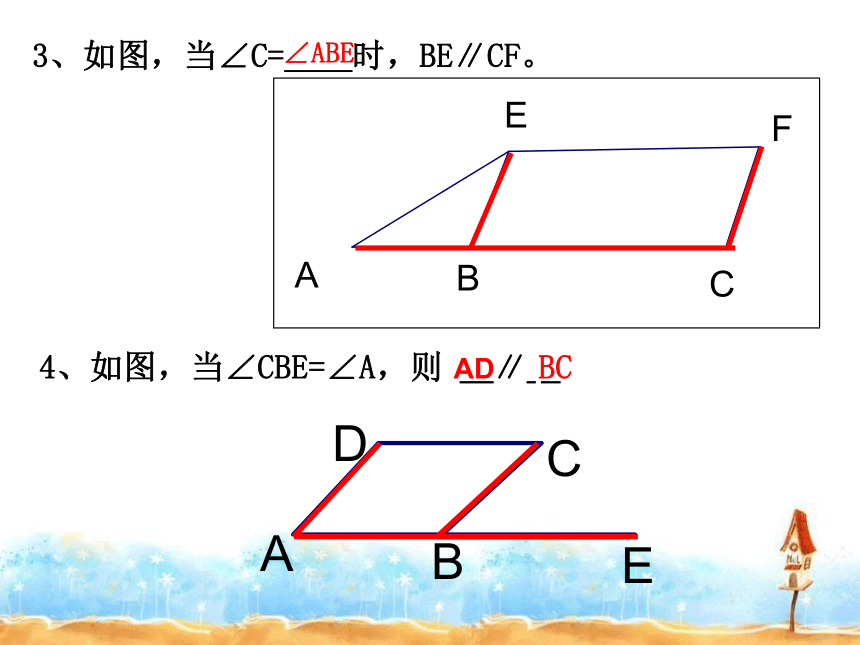
3、如图,当∠C=____时,BE∥CF。
4、如图,当∠CBE=∠A,则 _∥_
∠ABE
AD
BC
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
3
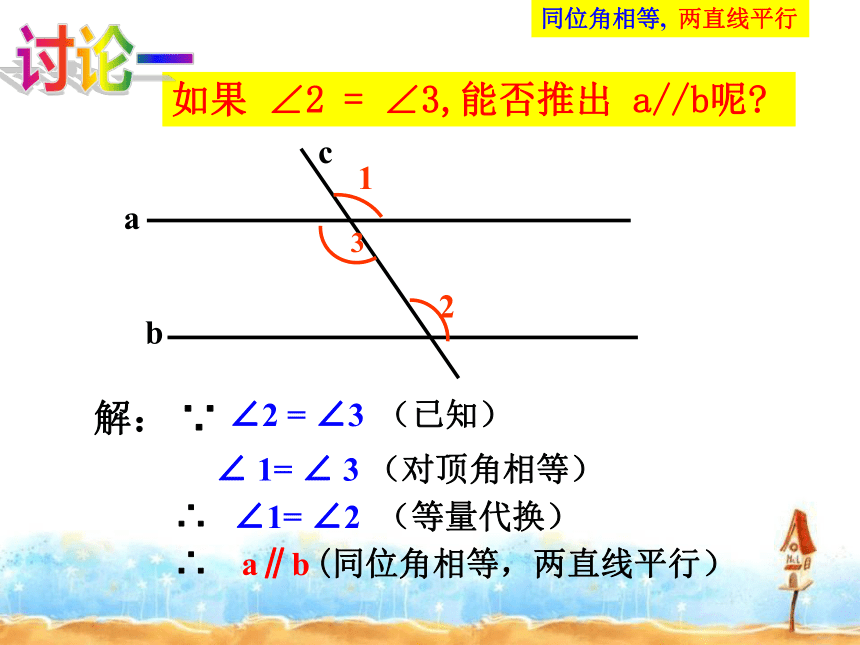
解: ∵
∠ 1= ∠ 3 (对顶角相等)
∴ ∠1= ∠2 (等量代换)
∴ a∥b
如果 ∠2 = ∠3,能否推出 a//b呢?
∠2 = ∠3
(已知)
同位角相等, 两直线平行
(同位角相等,两直线平行)
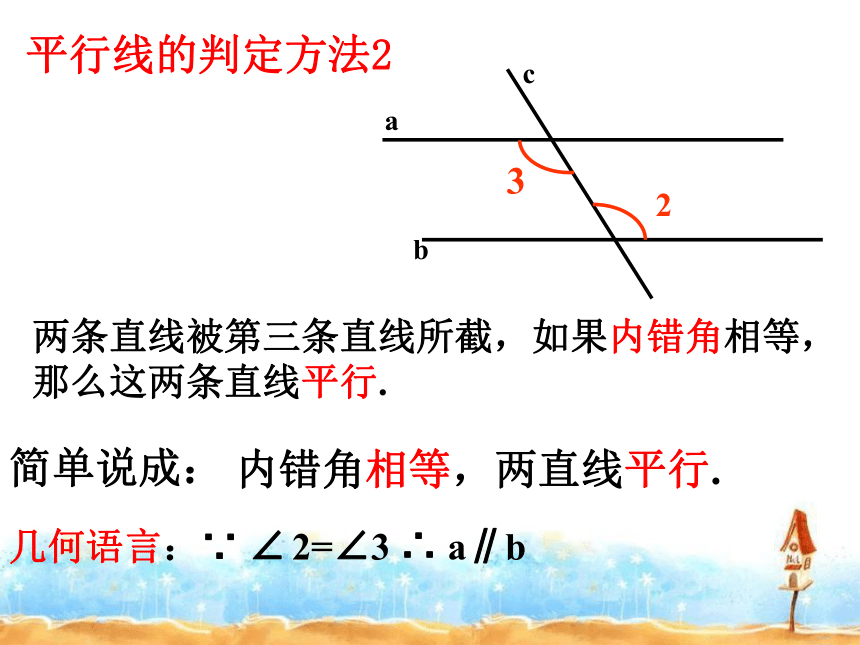
平行线的判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
1、如图所示,已知∠1=50°,
当∠2=___°时,a∥b。
2、如图所示,已知∠1=70°,
当∠3=___°时,a∥b。
再来一试
50
110
3、如图,当∠C=____ 时,AB∥CD。
4、如图,能判断AB∥CE的条件是_____
∠CBE
∠A=∠ACE
或∠B=∠ECD
如果 ∠2+ ∠4= 180o,能得到 a//b吗?
解:
∵ ∠1 + ∠4 = 180o
∠2 + ∠4 = 180o
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
a
b
c
1
2
3
4
解:
∵ ∠3 + ∠4 = 180o
∠2 + ∠4 = 180o
∴ ∠3 =∠2(同角的补角相等)
∴a∥b (内错角相等、两直线平行)
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
1、如图所示,已知∠1=50°,
当∠2=___°时,a∥b。
2、如图,当∠C+ ∠ __ =1800时,BC∥AD。
一试身手
130
ADC
如图所示:AC与BD相交于O,∠C=∠COD,∠A=∠AOB,
求证:AB∥CD
例1
∵∠C=∠COD, ∠A=∠AOB,
∠AOB=∠COD
∴∠A=∠C
∴AB ∥CD
证明:
已知∠3=45 °,∠1与∠2互余,你能得到
解:∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD
AB//CD吗?
例2
(1)∵∠1=∠B(已知)
∴__∥__(
(3)∵∠_ = ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
3 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
(4)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
AD BC 同旁内角互补,两直线平行
基础训练
本节课你学到了什么?
平行线的判定方法:
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
体验成功——达标检测
∠ C=60
当∠ABE= 时,EF∥CN
当∠CBF= 时,EF∥CN
。
1如图:
60°
60°
2、如图
(1)∵∠1=∠4(已知)
∴ ___∥___ ( )
(2)∵∠___ =∠___(已知)
∴AD∥BC ( )
(3)∵∠5=∠____(已知)
∴AB∥CD ( )
(4)∵∠A+∠ABC=1800(已知)
∴ ___∥___
ABC
当∠CBE= 时,EF∥CN
120°
内错角相等,两直线平行
内错角相等,两直线平行
同位角相等,两直线平行
(同旁内角互补,两直线平行)
3.如图所示,在下列条件中,不能判断L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4+∠5=180° D.∠2+∠4=180°
B
4.如图所示,已知∠1=120°,∠2=60°.试说明a与b的关系?
5.如图所示,已知∠OEB=130°∠FOD=25°,OF平分∠EOD,试说明AB∥CD
5.2.2 平行线的判定
1、在同一平面内,两直线的位置关系有__________
相交和平行
2、平行公理:
经过直线外一点, 一条直线与这条直线平行。
有且只有
3、思考:
我们该怎样画出过直线外一点与这条直线平行
的直线呢?
温故知新
1
2
观察思考
讨论交流
a
b
.
A
1、∠1和∠2是什么位置关系的角?
2、∠1和∠2度数相等吗?
3、要判断a//b你有办法了吗?
一贴
二靠
三推
四画
两条直线被第三条直线所截,如果
相等,那么这两条直线 。
同位角
平行
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行
平行线的判定方法1
同位角
平行
平行线的判定方法1
1、如图所示,已知∠1=60°,
当∠2=___°时,a∥b。
2、如图所示,已知∠1=60°,
当∠3=___°时,a∥b。
小试牛刀
60
120
3、如图,当∠C=____时,BE∥CF。
4、如图,当∠CBE=∠A,则 _∥_
∠ABE
AD
BC
两条直线被第三条直线所截,同时得到同位角、内错角和同旁内角,由同位角相等可以判定两直线平行,那么,能否利用内错角和同旁内角来判定两直线平行呢?
3
解: ∵
∠ 1= ∠ 3 (对顶角相等)
∴ ∠1= ∠2 (等量代换)
∴ a∥b
如果 ∠2 = ∠3,能否推出 a//b呢?
∠2 = ∠3
(已知)
同位角相等, 两直线平行
(同位角相等,两直线平行)
平行线的判定方法2
两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.
内错角相等,两直线平行.
简单说成:
1、如图所示,已知∠1=50°,
当∠2=___°时,a∥b。
2、如图所示,已知∠1=70°,
当∠3=___°时,a∥b。
再来一试
50
110
3、如图,当∠C=____ 时,AB∥CD。
4、如图,能判断AB∥CE的条件是_____
∠CBE
∠A=∠ACE
或∠B=∠ECD
如果 ∠2+ ∠4= 180o,能得到 a//b吗?
解:
∵ ∠1 + ∠4 = 180o
∠2 + ∠4 = 180o
∴ ∠1 =∠2(同角的补角相等)
∴a∥b (同位角相等、两直线平行)
a
b
c
1
2
3
4
解:
∵ ∠3 + ∠4 = 180o
∠2 + ∠4 = 180o
∴ ∠3 =∠2(同角的补角相等)
∴a∥b (内错角相等、两直线平行)
简单说成:
同旁内角互补,两直线平行
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.
1、如图所示,已知∠1=50°,
当∠2=___°时,a∥b。
2、如图,当∠C+ ∠ __ =1800时,BC∥AD。
一试身手
130
ADC
如图所示:AC与BD相交于O,∠C=∠COD,∠A=∠AOB,
求证:AB∥CD
例1
∵∠C=∠COD, ∠A=∠AOB,
∠AOB=∠COD
∴∠A=∠C
∴AB ∥CD
证明:
已知∠3=45 °,∠1与∠2互余,你能得到
解:∵∠1+∠2=90° ∠1=∠2
∴∠1=∠2=45°
∵ ∠3=45°
∴∠ 2=∠3
∴ AB∥CD
AB//CD吗?
例2
(1)∵∠1=∠B(已知)
∴__∥__(
(3)∵∠_ = ∠_(已知)
∴AB∥CD( )
AD BC 同位角相等,两直线平行)
(2)∵∠1=∠D(已知)
∴ ∥ ( )
3 5
内错角相等,两直线平行
AB DC 内错角相等,两直线平行
(4)∵∠B+∠BAD=180°(已知)
∴ ∥ ( )
AD BC 同旁内角互补,两直线平行
基础训练
本节课你学到了什么?
平行线的判定方法:
1、同位角相等,两直线平行
2、内错角相等,两直线平行
3、同旁内角互补,两直线平行
体验成功——达标检测
∠ C=60
当∠ABE= 时,EF∥CN
当∠CBF= 时,EF∥CN
。
1如图:
60°
60°
2、如图
(1)∵∠1=∠4(已知)
∴ ___∥___ ( )
(2)∵∠___ =∠___(已知)
∴AD∥BC ( )
(3)∵∠5=∠____(已知)
∴AB∥CD ( )
(4)∵∠A+∠ABC=1800(已知)
∴ ___∥___
ABC
当∠CBE= 时,EF∥CN
120°
内错角相等,两直线平行
内错角相等,两直线平行
同位角相等,两直线平行
(同旁内角互补,两直线平行)
3.如图所示,在下列条件中,不能判断L1∥L2的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4+∠5=180° D.∠2+∠4=180°
B
4.如图所示,已知∠1=120°,∠2=60°.试说明a与b的关系?
5.如图所示,已知∠OEB=130°∠FOD=25°,OF平分∠EOD,试说明AB∥CD
