六年级下册 数学 教案 -《探究圆柱表面积的巧算法》人教新课标(2014)
文档属性
| 名称 | 六年级下册 数学 教案 -《探究圆柱表面积的巧算法》人教新课标(2014) |  | |
| 格式 | zip | ||
| 文件大小 | 372.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 19:38:38 | ||
图片预览



文档简介
《探究圆柱表面积的巧算法》教学设计
【设计背景】
在教师的指导下,学生自主确定研究主题,在探索研究过程中积极主动地获取知识、应用知识、建构知识、解决问题,可以有效地提升学习能力,培养创新精神和综合实践素质。作为义务教育阶段的教师,精心发掘教材中的探究性教学内容就显得尤为重要。
这节课是六年级数学下册《圆柱和圆锥》教学完成后设计的一节探究课。这节课的教学内容有一定的现实性,因为表面积的普通算法很容易,但计算量大,学生感到难算、易出错;这个内容又有一定的价值,因为巧算法不但可以降低难度,还可以强化“转化”思想,上下底面的转化重现了“化圆为方”,图形的拼、切、组也体现了转化思想;这个内容也是有挑战性的,因为它依据课本又超出课本,是开发出的教学材料,因其生疏,才会更好地激发学生主动观察、主动实验、主动猜测、验证、推理、交流,这是有效的数学学习活动,可以有效地提升学生的学习兴趣、思维水平。
【课标与教材分析】
动手实践、主动探究和合作学习是小学阶段学习数学的重要方式,在探索研究过程中积极主动地获取知识、应用知识、建构知识、解决问题,可以有效地提升学习能力,培养创新精神和综合实践素质。本课是数学人教版义务教育教科书六年级下册第三单元《圆柱和圆锥》教学完成后设计的一节探究课,依据课本又超出课本,是开发出的教学材料,因学生对其生疏,才会更好地激发学生主动观察、主动实验、主动猜测、验证、推理、交流,这是有效的数学学习活动,可以有效地提升学生的学习兴趣、思维水平。
【学情分析】
六年级上册学生利用转化推导过圆的面积公式,现在已经直观认识了圆柱的基本特征,掌握了教材上圆柱表面积的计算方法。本课的教学内容具有一定的现实性,因为表面积的普通算法很容易,但计算量大,学生感到难算、易出错;本课的教学内容有特别的价值,因为巧算法不但可以降低计算难度,还可以强化转化思想。
【教学目标】
1.理解并掌握圆柱表面积的新算法,会运用新算法计算圆柱的表面积,解决有关的简单实际问题。
2.回顾并唤起对转化思想的认识,借助观察、尝试动手操作,组织小组合作,探究将圆柱展开图的三部分转化为规则图形,推导并归纳出圆柱表面积的巧算法。
3.通过圆柱表面积计算方法的探究,体会知识、思想、方法之间的联系性,进一步了解转化、推理、数形结合的数学思想在学习中的实际应用;在合作、探究、思考、交流、反思的过程中,进一步训练思维的严谨性,培养学科的理性精神。
【教学重点】推导圆柱表面积巧算法的过程;了解圆柱表面积的巧算法。
【教学难点】通过实践操作、合作交流,体会转化的数学思想。
【教学、具准备】小组合作,转化的数学思想。每名学生红、白A4纸各一张、胶棒(双面胶)、剪刀。
【教学过程】
一.复习旧知、提出探究课题
1.师:请同学们看大屏幕,回答以下三个问题。
(1)用什么数学方法推导出的圆的面积公式。
生:转化。
板书:转化。
师:转化是数学中一个非常重要的数学思想。
叙述推导圆的面积的过程。
生:将一个圆平均分成若干等份,拼成一个近似的长方形,长方形的长就是圆的周长的一半,长方形的宽就是圆的半径。
师:您回答的非常好,知识学习的很扎实。
求圆柱的表面积需要哪些基本条件?
生:需要知道圆柱的高和圆柱底面圆的半径。
师:你能用字母将圆柱的表面积公式表示出来吗?
生:S表=2πr×h+2×πr?(板书)
师:下面请同学们利用这个公式计算r=2cm,h=8cm的圆柱的表面积。
学生解答,教师巡视。
(4)师:在解题的过程中,你认为本题的难点在哪里呢?
生:方法简单,计算量大,容易出错。
师:有没有一种更简单、快捷的方法来计算圆柱的表面积呢?本节课,我们就一起探究圆柱表面积另外的计算方法。
板书:圆柱的表面积。
二.思考加工、明晰探究任务
师:要研究圆柱的表面积,首先应该知道圆柱的什么知识呢?
生:圆柱是由几部分组成的。
师:圆柱是由哪些部分组成的呢?
生:一个侧面,两个底面。
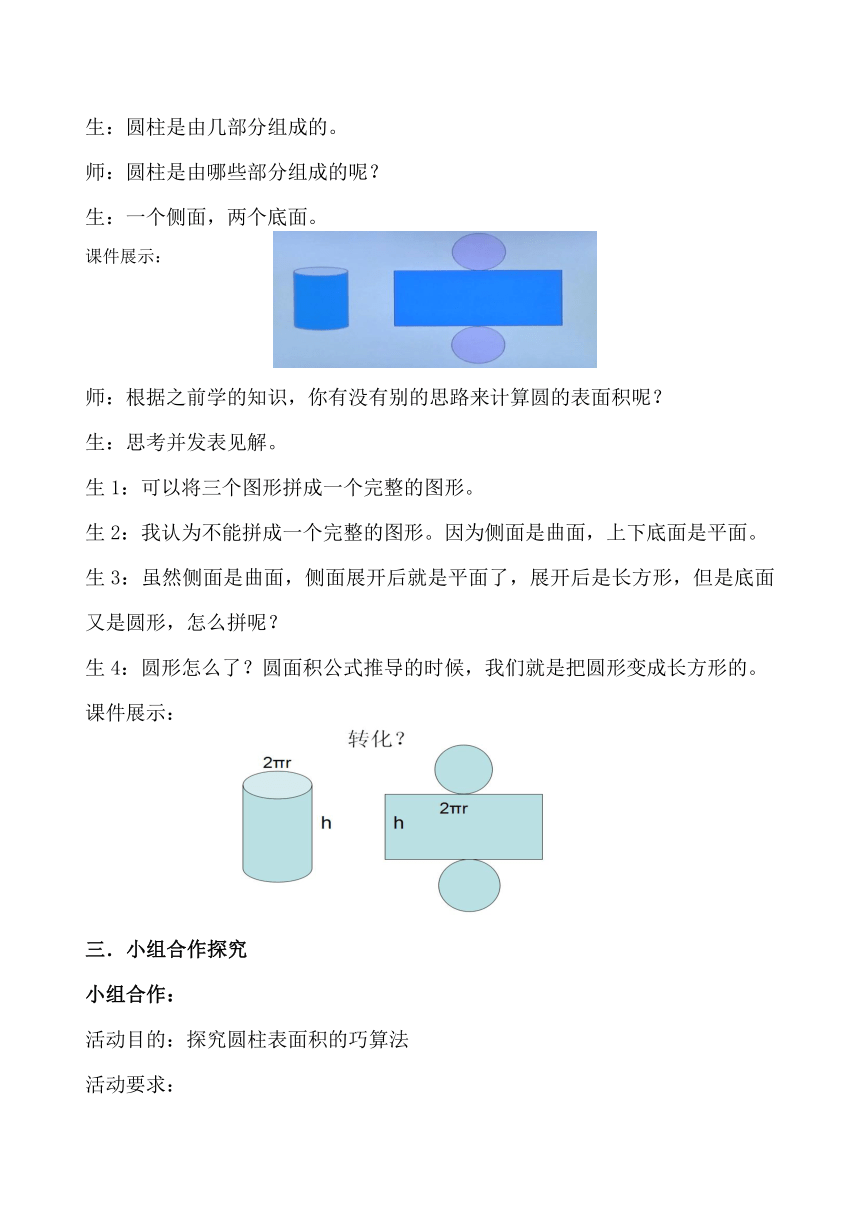
课件展示:
师:根据之前学的知识,你有没有别的思路来计算圆的表面积呢?
生:思考并发表见解。
生1:可以将三个图形拼成一个完整的图形。
生2:我认为不能拼成一个完整的图形。因为侧面是曲面,上下底面是平面。
生3:虽然侧面是曲面,侧面展开后就是平面了,展开后是长方形,但是底面又是圆形,怎么拼呢?
生4:圆形怎么了?圆面积公式推导的时候,我们就是把圆形变成长方形的。
课件展示:
三.小组合作探究
小组合作:
活动目的:探究圆柱表面积的巧算法
活动要求:
1.联系学过的内容,尝试将圆柱展开图的三部分转化成一个完整的规则图形。
2.先组内交流方法,再动手操作。
3.动手试一试,粘贴好转化后的图形,并用字母表示出图形各部分的名称。
4.思考、交流、总结圆柱表面积的新算法。
提醒:
1.可能需要调整粘贴位置,不要涂太多胶水。
2.用剪刀时要注意安全。
学生使用提前发的白色A4纸进行剪,粘贴在提前发的红色A4纸上。
四.汇报交流、获得结论
师:在小组合作过程中有没有遇到什么困难?你们又是怎么克服的呢?
预设:生:在对圆进行等份剪裁过程中,剪的份数不能过多,否则粘贴时候会很难粘贴。
小组汇报。(三个小组进行汇报,并进行讲解。)
小组1:平均分成8份。
小组2:平均分成12份。
小组3:平均分成16份。
师:通过三个小组的展示,你有什么发现吗?
生:我发现,分的份数越多,最后粘贴的图形越接近于长方形。
小组4:平均分成18份,粘贴后发现剩下一部分没有粘上。
师:现在你知道什么原因了吗?
生:在画长方形的时候,没有量圆的半径的长度,只是随意画了一个长方形。
课件展示:
板书:S表=c×(h+r)=2πr×(h+r)
师:现在请同学们再用现在得到的公式计算口算我们做的题目。
师:之前的公式:S表=2πr×h+2×πr?,我们是否可以借助之前学过的乘法分配律公式进行化简呢?通过观察,我们发现,可以提出2πr,从而得到:
S表=2πr×h+2×πr?
=2πr×(h+r)
这样,我们就从代数的角度也验证了我们新算法公式的正确性。
继续探究,无盖圆柱的表面积是否有巧算法
师:刚才我们探究了完整的圆柱的表面积的算法,那么无盖的情况下,能不能也有新的方法?
学生思考并发表见解。
无盖:
S表=2πr×(?r+h)
六.总结
在数学学习中,转化是很常用,也是很重要的一种思想,这节课我们也是利用转化的方法,推导出圆柱的表面积公式,可见,转化法在我们数学的学习过程中的作用非常大。希望同学们在今后的学习过程中,多思考,从不同的角度来理解问题,这样能够促进你们对数学的理解,也会感到数学原来是那么的有趣!
七.当堂练习
1.判断:
算式2×3.14×6×5+2×3.14×6?=2×3.14×6×(5+6)用了乘法的结合律。( )
2.计算下面圆柱的表面积。(利用新学的计算方法)
r=1cm,h=9cm d=6cm,h=7cm
3.一个有盖的水桶,底面半径为3分米,高为6分米。做这样的水桶,需要多大面积的铁皮?(接口处不计)
4.一个无盖的水桶,底面半径为3分米,高为6分米。做这样的水桶,需要多大面积的铁皮?(接口处不计)
八.板书
圆柱的表面积
转化
有盖:S表=2πr×h+2×πr? 无盖:S表=2πr×(?r+h)
=2πr×(h+r)
【设计背景】
在教师的指导下,学生自主确定研究主题,在探索研究过程中积极主动地获取知识、应用知识、建构知识、解决问题,可以有效地提升学习能力,培养创新精神和综合实践素质。作为义务教育阶段的教师,精心发掘教材中的探究性教学内容就显得尤为重要。
这节课是六年级数学下册《圆柱和圆锥》教学完成后设计的一节探究课。这节课的教学内容有一定的现实性,因为表面积的普通算法很容易,但计算量大,学生感到难算、易出错;这个内容又有一定的价值,因为巧算法不但可以降低难度,还可以强化“转化”思想,上下底面的转化重现了“化圆为方”,图形的拼、切、组也体现了转化思想;这个内容也是有挑战性的,因为它依据课本又超出课本,是开发出的教学材料,因其生疏,才会更好地激发学生主动观察、主动实验、主动猜测、验证、推理、交流,这是有效的数学学习活动,可以有效地提升学生的学习兴趣、思维水平。
【课标与教材分析】
动手实践、主动探究和合作学习是小学阶段学习数学的重要方式,在探索研究过程中积极主动地获取知识、应用知识、建构知识、解决问题,可以有效地提升学习能力,培养创新精神和综合实践素质。本课是数学人教版义务教育教科书六年级下册第三单元《圆柱和圆锥》教学完成后设计的一节探究课,依据课本又超出课本,是开发出的教学材料,因学生对其生疏,才会更好地激发学生主动观察、主动实验、主动猜测、验证、推理、交流,这是有效的数学学习活动,可以有效地提升学生的学习兴趣、思维水平。
【学情分析】
六年级上册学生利用转化推导过圆的面积公式,现在已经直观认识了圆柱的基本特征,掌握了教材上圆柱表面积的计算方法。本课的教学内容具有一定的现实性,因为表面积的普通算法很容易,但计算量大,学生感到难算、易出错;本课的教学内容有特别的价值,因为巧算法不但可以降低计算难度,还可以强化转化思想。
【教学目标】
1.理解并掌握圆柱表面积的新算法,会运用新算法计算圆柱的表面积,解决有关的简单实际问题。
2.回顾并唤起对转化思想的认识,借助观察、尝试动手操作,组织小组合作,探究将圆柱展开图的三部分转化为规则图形,推导并归纳出圆柱表面积的巧算法。
3.通过圆柱表面积计算方法的探究,体会知识、思想、方法之间的联系性,进一步了解转化、推理、数形结合的数学思想在学习中的实际应用;在合作、探究、思考、交流、反思的过程中,进一步训练思维的严谨性,培养学科的理性精神。
【教学重点】推导圆柱表面积巧算法的过程;了解圆柱表面积的巧算法。
【教学难点】通过实践操作、合作交流,体会转化的数学思想。
【教学、具准备】小组合作,转化的数学思想。每名学生红、白A4纸各一张、胶棒(双面胶)、剪刀。
【教学过程】
一.复习旧知、提出探究课题
1.师:请同学们看大屏幕,回答以下三个问题。
(1)用什么数学方法推导出的圆的面积公式。
生:转化。
板书:转化。
师:转化是数学中一个非常重要的数学思想。
叙述推导圆的面积的过程。
生:将一个圆平均分成若干等份,拼成一个近似的长方形,长方形的长就是圆的周长的一半,长方形的宽就是圆的半径。
师:您回答的非常好,知识学习的很扎实。
求圆柱的表面积需要哪些基本条件?
生:需要知道圆柱的高和圆柱底面圆的半径。
师:你能用字母将圆柱的表面积公式表示出来吗?
生:S表=2πr×h+2×πr?(板书)
师:下面请同学们利用这个公式计算r=2cm,h=8cm的圆柱的表面积。
学生解答,教师巡视。
(4)师:在解题的过程中,你认为本题的难点在哪里呢?
生:方法简单,计算量大,容易出错。
师:有没有一种更简单、快捷的方法来计算圆柱的表面积呢?本节课,我们就一起探究圆柱表面积另外的计算方法。
板书:圆柱的表面积。
二.思考加工、明晰探究任务
师:要研究圆柱的表面积,首先应该知道圆柱的什么知识呢?
生:圆柱是由几部分组成的。
师:圆柱是由哪些部分组成的呢?
生:一个侧面,两个底面。
课件展示:
师:根据之前学的知识,你有没有别的思路来计算圆的表面积呢?
生:思考并发表见解。
生1:可以将三个图形拼成一个完整的图形。
生2:我认为不能拼成一个完整的图形。因为侧面是曲面,上下底面是平面。
生3:虽然侧面是曲面,侧面展开后就是平面了,展开后是长方形,但是底面又是圆形,怎么拼呢?
生4:圆形怎么了?圆面积公式推导的时候,我们就是把圆形变成长方形的。
课件展示:
三.小组合作探究
小组合作:
活动目的:探究圆柱表面积的巧算法
活动要求:
1.联系学过的内容,尝试将圆柱展开图的三部分转化成一个完整的规则图形。
2.先组内交流方法,再动手操作。
3.动手试一试,粘贴好转化后的图形,并用字母表示出图形各部分的名称。
4.思考、交流、总结圆柱表面积的新算法。
提醒:
1.可能需要调整粘贴位置,不要涂太多胶水。
2.用剪刀时要注意安全。
学生使用提前发的白色A4纸进行剪,粘贴在提前发的红色A4纸上。
四.汇报交流、获得结论
师:在小组合作过程中有没有遇到什么困难?你们又是怎么克服的呢?
预设:生:在对圆进行等份剪裁过程中,剪的份数不能过多,否则粘贴时候会很难粘贴。
小组汇报。(三个小组进行汇报,并进行讲解。)
小组1:平均分成8份。
小组2:平均分成12份。
小组3:平均分成16份。
师:通过三个小组的展示,你有什么发现吗?
生:我发现,分的份数越多,最后粘贴的图形越接近于长方形。
小组4:平均分成18份,粘贴后发现剩下一部分没有粘上。
师:现在你知道什么原因了吗?
生:在画长方形的时候,没有量圆的半径的长度,只是随意画了一个长方形。
课件展示:
板书:S表=c×(h+r)=2πr×(h+r)
师:现在请同学们再用现在得到的公式计算口算我们做的题目。
师:之前的公式:S表=2πr×h+2×πr?,我们是否可以借助之前学过的乘法分配律公式进行化简呢?通过观察,我们发现,可以提出2πr,从而得到:
S表=2πr×h+2×πr?
=2πr×(h+r)
这样,我们就从代数的角度也验证了我们新算法公式的正确性。
继续探究,无盖圆柱的表面积是否有巧算法
师:刚才我们探究了完整的圆柱的表面积的算法,那么无盖的情况下,能不能也有新的方法?
学生思考并发表见解。
无盖:
S表=2πr×(?r+h)
六.总结
在数学学习中,转化是很常用,也是很重要的一种思想,这节课我们也是利用转化的方法,推导出圆柱的表面积公式,可见,转化法在我们数学的学习过程中的作用非常大。希望同学们在今后的学习过程中,多思考,从不同的角度来理解问题,这样能够促进你们对数学的理解,也会感到数学原来是那么的有趣!
七.当堂练习
1.判断:
算式2×3.14×6×5+2×3.14×6?=2×3.14×6×(5+6)用了乘法的结合律。( )
2.计算下面圆柱的表面积。(利用新学的计算方法)
r=1cm,h=9cm d=6cm,h=7cm
3.一个有盖的水桶,底面半径为3分米,高为6分米。做这样的水桶,需要多大面积的铁皮?(接口处不计)
4.一个无盖的水桶,底面半径为3分米,高为6分米。做这样的水桶,需要多大面积的铁皮?(接口处不计)
八.板书
圆柱的表面积
转化
有盖:S表=2πr×h+2×πr? 无盖:S表=2πr×(?r+h)
=2πr×(h+r)
