六年级下册 数学 教案 -《解决问题的策略——转化》人教新课标(2014)
文档属性
| 名称 | 六年级下册 数学 教案 -《解决问题的策略——转化》人教新课标(2014) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-17 20:15:52 | ||
图片预览



文档简介
《解决问题的策略--转化》教学设计
【学习内容】六年级总复习《解决问题策略--转化》
【课程标准描述】
形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神。
【学习目标】
1.学生初步学会运用转化的策略分析问题,并能根据问题的特点确定具体的转化方法,从而有效解决实际问题。
2.学生通过对解决问题过程的反思,感受解决问题策略的特点和价值,进一步培养思维的条理性和严密性。
3.学生通过学习,进一步积累解决问题的实际经验,增强解决问题的策略意识,获得解决问题的成功体验。
【学习重点】感受“转化”策略的价值,初步掌握转化??的方法和技巧。
【学习难点】灵活运用“转化”的策略解决问题。
【评价活动方案】
1.通过直观演示,初步感悟转化,以评价学习目标1。
2.通过回忆经历过的转化活动,体会转化策略的应用过程,感受解决问题策略的特点和价值,以评价学习目标2。
3.通过实践应用,增强解决问题的策略意识,以及应用转化策略解决实际问题,以评价学习目标3。
【学习过程】
1、游戏导入,激发兴趣
1.同学们,上课之前咱们先来玩个游戏,看屏幕上是什么?(一头牛!)你知道一头牛有几只眼睛?几条腿?几条尾巴?喂什么?(为什么?)到底为什么呢?看看问题你一定就清楚了,(出示喂什么?)你怎么笑了?看来有些时候需要一定的联想力。
2.72小时,猜一字。(晶)你是怎么想到谜底的?
在不知不觉中他就运用了一种非常重要的解决问题的策略——转化。接下来的40分钟就让我们一起走进转化的世界去来领略转化的神奇。这节课我们就来一起研究解决问题的策略——转化。(板书课题)
2、自主探究,合作交流
(一)直观演示,感受转化 (评价目标1)
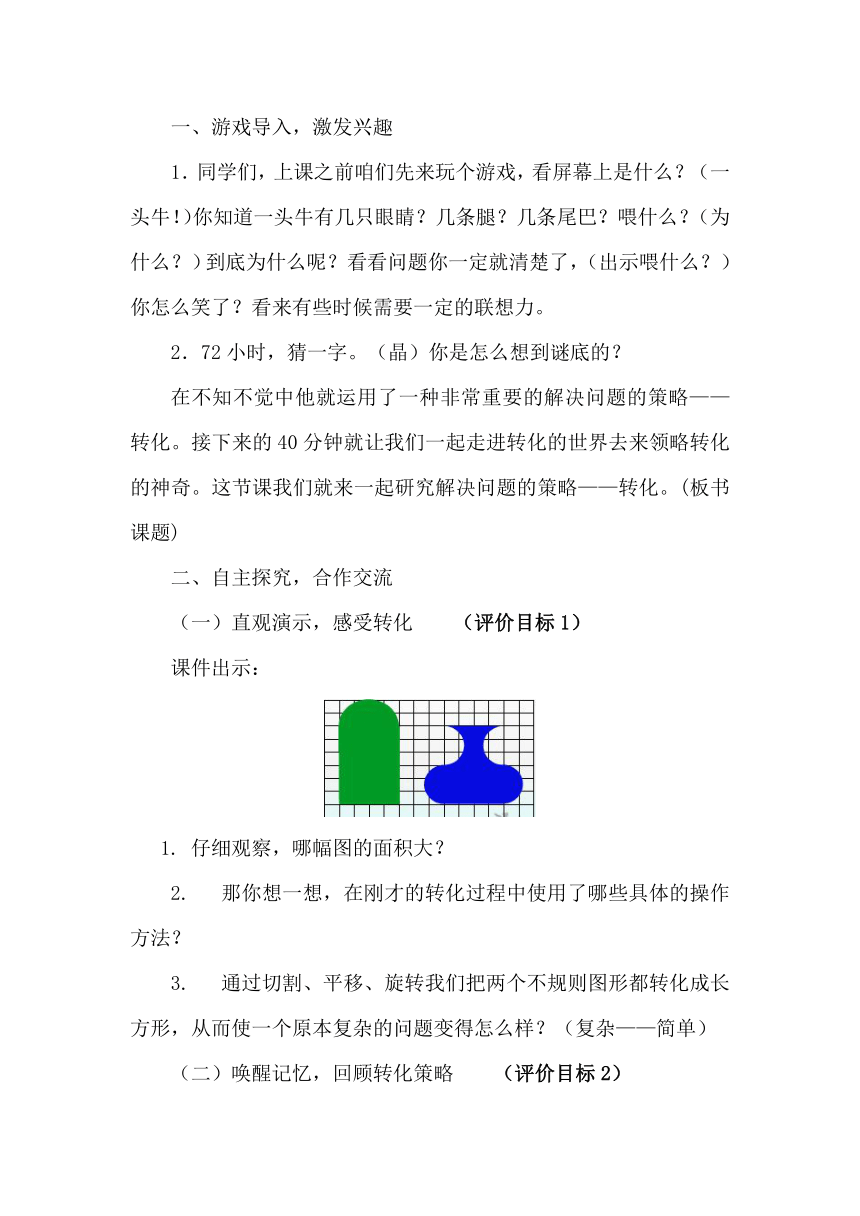
课件出示:?
1. 仔细观察,哪幅图的面积大?
2. 那你想一想,在刚才的转化过程中使用了哪些具体的操作方法?
3. 通过切割、平移、旋转我们把两个不规则图形都转化成长方形,从而使一个原本复杂的问题变得怎么样?(复杂——简单)
(二)唤醒记忆,回顾转化策略 (评价目标2)
1.其实转化在我们以往的数学学习中经常用到,而且用它解决过许多问题。回想一下,哪用到过?(面积,体积,计算)
2.在这三个领域中我们是怎样利用转化来解决这些问题的呢?每个小组都有一张学习单,下面以4人小组为单位,选择其中的一个领域研究一下,把转化的过程画一画、写一写、说一说,看哪个小组最先完成,开始。
3.汇报:(1)面积领域的转化
预设1:通过切割、平移,把平行四边行转化成长方形。
预设2:通过旋转、平移,把两个完全一样的三角形转化成了平行四边形。
预设3:通过旋转、平移,把两个完全一样的梯形转化成平行四边形。
预设4:通过切割、拼插,把圆转化成长方形。
(2)体积领域的转化
预设1:通过把圆柱体切割,拼插的方法将其拼插转化成圆柱体。
预设2:通过实验的方法,向圆锥体模型中注入水或沙子,将其倒入等底等高的圆柱体模型中,把圆锥的体积转化成圆柱体积的三分之一。
(3)计算领域的转化
预设1:小数乘法是转化为整数乘法。
预设2:分数除法是转化为分数乘法。
预设3:除数是小数除法转化为除数是整数的除法。
预设4:异分母分数加减法通过通分转化成同分母分数。
(4)小结:同学们说了这么多,看来转化在我们数学学习中的应用真的是太广泛了。一起来看一下。通过数方格,我们学会了长方形面积的计算方法,而在学习平行四边形和圆形的面积时,就转化成了学过的长方形,在学习三角形和梯形的面积时,又转化成了学过的平行四边形。以及应用转化来解决体积的问题。计算问题时,它们有一个共同点,就是当我们遇到一个新的问题,不会解决的问题时怎么办?(转化成以前学过的)。总结的真好,也就是把未知——已知。只不过转化的方法不尽相同。
(三)实践应用,体验转化策略 (评价目标3)
1.巧用转化写分数
图形一 图形二 图形三
三个图形,先独立思考,如果遇到困难,同桌交流,开始。
图形一预设:利用旋转、移动阴影部分占整个圆的四分之一。
图形二预设:利用平移,阴影部分占整个长方形面积的二分之一。
这个可不那么明显了,怎么办?尝试一下转化?
图形三预设1:把中间图形在绕中心旋转180°,就不难看出阴影部分的面积是整个图形面积的明显四分之一。
图形三预设2:将中间的三角形移动,与大三角形上方一个角重合,就可以看出阴影部分的面积是整个图形面积的四分之一。
小结:同学们,通过平移或旋转,我们把一个关系不明显的图形转化成了如此明显的关系,也就是把未知关系转化成已知。让我们一目了然的看出涂色部分占了整个图形的四分之一,同学们,你们说转化方法好用吧,所以我们一起要勇于转化,乐于转化。
2. 怎样知道涂色部分面积的和是多少?
(1)同学们可以在练习本上自己试着画一画,谁来说说你的想法?问问大家有问题吗?
预设:我们可以将这三个阴影部分拼成一个半圆。因为圆周角的度数是360°,三角形内角和的度数是180°。所以能拼成一个半圆。
(2)我来请教小老师一个问题吧,为什么涂色部分可以拼成一个半圆?只具备这一个条件就可以吗?
预设:还需要这3个扇形的半径相等,这3个扇形半径都是2厘米,所以能拼成一个半圆。
是啊,只有具备了这两个条件才可以拼成一个半圆。看来转化也是有条件的。一起来看看,利用旋转、平移,把涂色部分的面积和转化成了半圆的面积。
(3)怎样列式?
(4)小结:像这样把零散部分拼成一个整体,这种转化方法我们给它起个名字叫什么呢?大胆试试说说零拼整的转化方法。
3.一个圆柱形玻璃容器底面直径是10厘米,里面装有6厘米深的水。现在把一块石块放入容器中,水面上升到8厘米。这块石块的体积是多少?
(1)自己读题,理解题意,会怎么?在练习本上只列式不计算。
(2)谁来说说你的思路。
预设:不规则物体石块的体积转化成上升高为2厘米水的圆柱体体积。(动画演示。)
(3)怎么列式?
4.
(1)你想怎么做?通分吗?那怎么办?同学们别着急,当我们遇到这样复杂的问题而无从下手的时候,不妨以退为进。从比较简单的一部分开始研究,如果能从中发现规律的话,自然可以利用规律来解决复杂的问题。接受吗?
现在我们就先研究一下有想法吗?有的有,有的没有,如果实在没有的话,给你一个正方形表示1,利用它来试一试,可以集合四人小组的智慧,赶快研究吧。
(2)学生汇报:
预设1:我们可以利用拆分法。
预设2:利用数形结合,把求的和转化成了用1-空白的。
(3)如果继续加+ 怎么求? 再加一个该加多少了?怎么求?
(4)
这个复杂的问题可以解决了吗?怎么求?
三、交流收获,全课小结
真棒,我觉得我们不得不佩服自己,更要佩服转化这种策略。通过这些具体的转化方法,当然还有很多......我们可以把一个复杂的问题变得简单,把未知问题变成已知,从而巧妙的解决问题。其实在我们的数学学习中除了转化这种解题策略还有许多其他的,比如假设,替换,倒推等等,如果感兴趣的话课下可以继续研究。下课。
【学习目标检测】
1.用分数表示图中涂色的部分。
2.9999-999-99-9可以转化成怎样的算式来计算?先想一想再算出结果?
【学习内容】六年级总复习《解决问题策略--转化》
【课程标准描述】
形成解决问题的一些基本策略,体验解决问题策略的多样性,发展实践能力与创新精神。
【学习目标】
1.学生初步学会运用转化的策略分析问题,并能根据问题的特点确定具体的转化方法,从而有效解决实际问题。
2.学生通过对解决问题过程的反思,感受解决问题策略的特点和价值,进一步培养思维的条理性和严密性。
3.学生通过学习,进一步积累解决问题的实际经验,增强解决问题的策略意识,获得解决问题的成功体验。
【学习重点】感受“转化”策略的价值,初步掌握转化??的方法和技巧。
【学习难点】灵活运用“转化”的策略解决问题。
【评价活动方案】
1.通过直观演示,初步感悟转化,以评价学习目标1。
2.通过回忆经历过的转化活动,体会转化策略的应用过程,感受解决问题策略的特点和价值,以评价学习目标2。
3.通过实践应用,增强解决问题的策略意识,以及应用转化策略解决实际问题,以评价学习目标3。
【学习过程】
1、游戏导入,激发兴趣
1.同学们,上课之前咱们先来玩个游戏,看屏幕上是什么?(一头牛!)你知道一头牛有几只眼睛?几条腿?几条尾巴?喂什么?(为什么?)到底为什么呢?看看问题你一定就清楚了,(出示喂什么?)你怎么笑了?看来有些时候需要一定的联想力。
2.72小时,猜一字。(晶)你是怎么想到谜底的?
在不知不觉中他就运用了一种非常重要的解决问题的策略——转化。接下来的40分钟就让我们一起走进转化的世界去来领略转化的神奇。这节课我们就来一起研究解决问题的策略——转化。(板书课题)
2、自主探究,合作交流
(一)直观演示,感受转化 (评价目标1)
课件出示:?
1. 仔细观察,哪幅图的面积大?
2. 那你想一想,在刚才的转化过程中使用了哪些具体的操作方法?
3. 通过切割、平移、旋转我们把两个不规则图形都转化成长方形,从而使一个原本复杂的问题变得怎么样?(复杂——简单)
(二)唤醒记忆,回顾转化策略 (评价目标2)
1.其实转化在我们以往的数学学习中经常用到,而且用它解决过许多问题。回想一下,哪用到过?(面积,体积,计算)
2.在这三个领域中我们是怎样利用转化来解决这些问题的呢?每个小组都有一张学习单,下面以4人小组为单位,选择其中的一个领域研究一下,把转化的过程画一画、写一写、说一说,看哪个小组最先完成,开始。
3.汇报:(1)面积领域的转化
预设1:通过切割、平移,把平行四边行转化成长方形。
预设2:通过旋转、平移,把两个完全一样的三角形转化成了平行四边形。
预设3:通过旋转、平移,把两个完全一样的梯形转化成平行四边形。
预设4:通过切割、拼插,把圆转化成长方形。
(2)体积领域的转化
预设1:通过把圆柱体切割,拼插的方法将其拼插转化成圆柱体。
预设2:通过实验的方法,向圆锥体模型中注入水或沙子,将其倒入等底等高的圆柱体模型中,把圆锥的体积转化成圆柱体积的三分之一。
(3)计算领域的转化
预设1:小数乘法是转化为整数乘法。
预设2:分数除法是转化为分数乘法。
预设3:除数是小数除法转化为除数是整数的除法。
预设4:异分母分数加减法通过通分转化成同分母分数。
(4)小结:同学们说了这么多,看来转化在我们数学学习中的应用真的是太广泛了。一起来看一下。通过数方格,我们学会了长方形面积的计算方法,而在学习平行四边形和圆形的面积时,就转化成了学过的长方形,在学习三角形和梯形的面积时,又转化成了学过的平行四边形。以及应用转化来解决体积的问题。计算问题时,它们有一个共同点,就是当我们遇到一个新的问题,不会解决的问题时怎么办?(转化成以前学过的)。总结的真好,也就是把未知——已知。只不过转化的方法不尽相同。
(三)实践应用,体验转化策略 (评价目标3)
1.巧用转化写分数
图形一 图形二 图形三
三个图形,先独立思考,如果遇到困难,同桌交流,开始。
图形一预设:利用旋转、移动阴影部分占整个圆的四分之一。
图形二预设:利用平移,阴影部分占整个长方形面积的二分之一。
这个可不那么明显了,怎么办?尝试一下转化?
图形三预设1:把中间图形在绕中心旋转180°,就不难看出阴影部分的面积是整个图形面积的明显四分之一。
图形三预设2:将中间的三角形移动,与大三角形上方一个角重合,就可以看出阴影部分的面积是整个图形面积的四分之一。
小结:同学们,通过平移或旋转,我们把一个关系不明显的图形转化成了如此明显的关系,也就是把未知关系转化成已知。让我们一目了然的看出涂色部分占了整个图形的四分之一,同学们,你们说转化方法好用吧,所以我们一起要勇于转化,乐于转化。
2. 怎样知道涂色部分面积的和是多少?
(1)同学们可以在练习本上自己试着画一画,谁来说说你的想法?问问大家有问题吗?
预设:我们可以将这三个阴影部分拼成一个半圆。因为圆周角的度数是360°,三角形内角和的度数是180°。所以能拼成一个半圆。
(2)我来请教小老师一个问题吧,为什么涂色部分可以拼成一个半圆?只具备这一个条件就可以吗?
预设:还需要这3个扇形的半径相等,这3个扇形半径都是2厘米,所以能拼成一个半圆。
是啊,只有具备了这两个条件才可以拼成一个半圆。看来转化也是有条件的。一起来看看,利用旋转、平移,把涂色部分的面积和转化成了半圆的面积。
(3)怎样列式?
(4)小结:像这样把零散部分拼成一个整体,这种转化方法我们给它起个名字叫什么呢?大胆试试说说零拼整的转化方法。
3.一个圆柱形玻璃容器底面直径是10厘米,里面装有6厘米深的水。现在把一块石块放入容器中,水面上升到8厘米。这块石块的体积是多少?
(1)自己读题,理解题意,会怎么?在练习本上只列式不计算。
(2)谁来说说你的思路。
预设:不规则物体石块的体积转化成上升高为2厘米水的圆柱体体积。(动画演示。)
(3)怎么列式?
4.
(1)你想怎么做?通分吗?那怎么办?同学们别着急,当我们遇到这样复杂的问题而无从下手的时候,不妨以退为进。从比较简单的一部分开始研究,如果能从中发现规律的话,自然可以利用规律来解决复杂的问题。接受吗?
现在我们就先研究一下有想法吗?有的有,有的没有,如果实在没有的话,给你一个正方形表示1,利用它来试一试,可以集合四人小组的智慧,赶快研究吧。
(2)学生汇报:
预设1:我们可以利用拆分法。
预设2:利用数形结合,把求的和转化成了用1-空白的。
(3)如果继续加+ 怎么求? 再加一个该加多少了?怎么求?
(4)
这个复杂的问题可以解决了吗?怎么求?
三、交流收获,全课小结
真棒,我觉得我们不得不佩服自己,更要佩服转化这种策略。通过这些具体的转化方法,当然还有很多......我们可以把一个复杂的问题变得简单,把未知问题变成已知,从而巧妙的解决问题。其实在我们的数学学习中除了转化这种解题策略还有许多其他的,比如假设,替换,倒推等等,如果感兴趣的话课下可以继续研究。下课。
【学习目标检测】
1.用分数表示图中涂色的部分。
2.9999-999-99-9可以转化成怎样的算式来计算?先想一想再算出结果?
