江西省“山江湖”协作体2019-2020学年高一(自主班)上学期第一次联考数学(2)试卷 Word版含答案
文档属性
| 名称 | 江西省“山江湖”协作体2019-2020学年高一(自主班)上学期第一次联考数学(2)试卷 Word版含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 242.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 15:16:56 | ||
图片预览



文档简介
山江湖协作体联考高二数学试卷(理科)(自主班)
时间:120分钟 满分:150分
第Ⅰ卷
选择题:共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.若集合A={x|x2+x-6<0},B={x|≤0},则A∩B等于( )
A.(-3,3) B.(-2,2) C.[-2,2) D.[-2,3)
2.有下列函数:①y=x+(x>0);②y=x++1(x>1);③y=cosx+(00).其中最小值为4的函数有( )
A.1个 B.2个 C.3个 D.4个
3.互不相等的三个正数成等差数列,是a,b的等比中项,是b,c的等比中项,那么,,三个数( )
(A)成等差数列不成等比数列 (B)成等比数列不成等差数列
(C)既成等差数列又成等比数列 (D)既不成等差数列,又不成等比数列
4.直线xcos+ysin+1=0,的倾斜角是( )
A. B. C. D.
5.设是非零向量若函数的图象是一条直线则必有( )
A. B. C. D.
6.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有( )种
A.1080个 B.1280 C.2160个 D.4320
7.某程序框图如右图所示,若输出的S=57,则判断框内填( )
A、k4? B、k5? C、k6? D、k7?
已知a>0,x、y满足约束条件
若z=2x+y的最小值为1,则a=( )
A.2 B. 1 C. D.
9.在矩形中,,若向该矩形内随投一点,那么使得与的面积都不小于2的概率为( )
A. B. C. D.
10.设m,n为正实数,若直线(m+1)x+(n+1)y-4=0与圆x2+y2-4x-4y+4=0相切,则mn( )
A.有最小值1+,无最大值 B.有最小值3-2,最大值3+2
C.有最大值3+2,无最小值 D.有最小值3+2,无最大值
11.已知函数,若,使得成立,则实数的取值范围是( )
A. B. C. D.
12.已知函数满足,当时,;当时,,若函数在上有五个零点,则的最小值为( )
A. B. C. D.
第Ⅱ卷
二.填空题:本大题共四小题,每小题5分,共20分。
13.△ABC中,a、b是它的两边,S是△ABC的面积,若,则△ABC的形状为
14.设的展开式中的常数项为-16,则 .
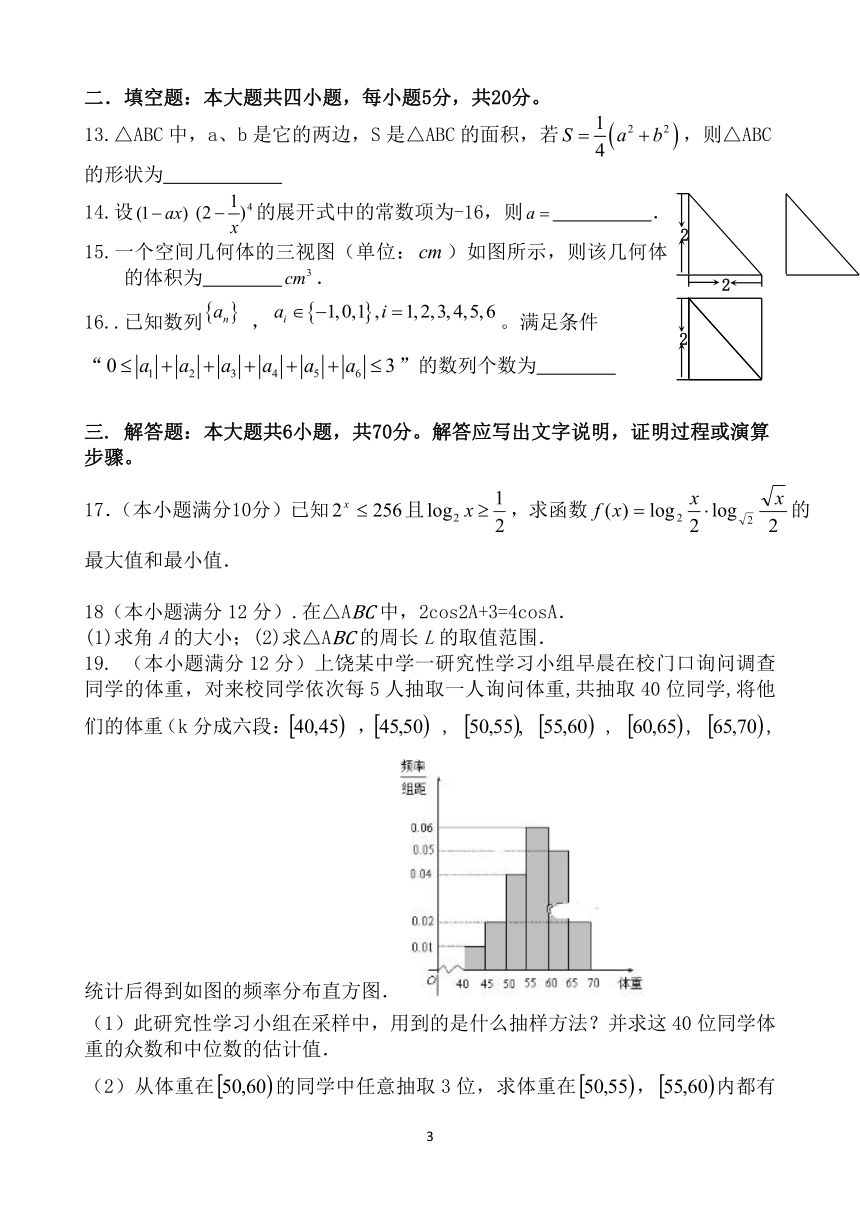
15.一个空间几何体的三视图(单位:)如图所示,则该几何体的体积为 .
16..已知数列 ,。满足条件
“”的数列个数为
三. 解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)已知且,求函数的最大值和最小值.
18(本小题满分12分).在△ABC中,2cos2A+3=4cosA. (1)求角A的大小;(2)求△ABC的周长L的取值范围.
19. (本小题满分12分)上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(k分成六段: , , , , , 统计后得到如图的频率分布直方图.
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在的同学中任意抽取3位,求体重在,内都有同学的概率.
20. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求证:平面平面;
(2)证明平面平面,并求出到平面的距离.
21.(本小题满分12分)在平面直角坐标系中,曲线与坐标轴的交点都在圆上
(Ⅰ)求圆的方程;
(Ⅱ)若圆与直线交与两点,且,求的值
22(本小题满分12分).已知数列满足,且.
(1)证明:数列为等比数列;
(2)设,记数列的前项和为,若对任意的,恒成立,求的取值范围.
高二数学(理)试卷答案及评分标准(自主班)
一、选择题:共12小题,每小题5分,满分60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
C
A
A
B
C
D
D
B
A
二、填空题:共4小题,每小题5分,共20分.
13. 等腰直角三角形. 14. -1 ; 15.; 16. 233
17.(本小题满分10分)
解:由得,即 …………………4分
. …………………8分
当,当 …………………10分
18.(本小题满分12分)
(1)因为2cos2A+3=4cosA,所以2cos2A+=2cosA,
所以4cos2A-4cosA+1=0,所以cosA=,又因为0(2)因为所以b=
所以(sinB+sinC).
因为B+C=,所以
又因为0(本小题满分12分)
解(1)系统抽样,57.5, 57.5; ……………………………6分
(2)
……………………12分
(本小题满分12分)
(1)分别是线段的中点,所以,又为正方形,,
所以,
又平面,所以平面.
因为分别是线段的中点,所以,
又平面,所以,平面.
所以平面平面. ………………………………5分
(2)因为,,,所以平面,
又,所以平面,所以平面平面.
取中点,连接,则,平面即为平面,
在平面内,作,垂足为,则平面,
即为到平面的距离, ………………………10分
在三角形中,为中点,.………12分
(本小题满分12分)
(Ⅰ)曲线与轴交于点,与与轴交于点
因而圆心坐标为则有.
半径为,所以圆方程是. ………6分
(Ⅱ)解法一:设点满足
解得:.
.
解得,满足,
………………………………12分
解法二:设经过直线和圆的交点的圆的方程为
,若,则以AB为直径的圆过坐标原点
设上述圆就是这样的圆,则圆过原点,所以 ①
同时,该圆的圆心在直线上,化简得 ②
由①②求得。
(本小题满分12分)
(1)证明:因为,所以
即,则
从而数列是以6为首项,2为公比的等比数列 ………………4分
(2)解:由(1)知,即
所以………6分
当为偶数时,
………………8分
当为奇数时,
………………10分
当为偶数时,是递减的,此时当时,取最大值,则;
当为奇数时,是递增的,此时,则.
综上,的取值范围是. ……………12分
时间:120分钟 满分:150分
第Ⅰ卷
选择题:共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项是符合题目要求的一项。
1.若集合A={x|x2+x-6<0},B={x|≤0},则A∩B等于( )
A.(-3,3) B.(-2,2) C.[-2,2) D.[-2,3)
2.有下列函数:①y=x+(x>0);②y=x++1(x>1);③y=cosx+(0
A.1个 B.2个 C.3个 D.4个
3.互不相等的三个正数成等差数列,是a,b的等比中项,是b,c的等比中项,那么,,三个数( )
(A)成等差数列不成等比数列 (B)成等比数列不成等差数列
(C)既成等差数列又成等比数列 (D)既不成等差数列,又不成等比数列
4.直线xcos+ysin+1=0,的倾斜角是( )
A. B. C. D.
5.设是非零向量若函数的图象是一条直线则必有( )
A. B. C. D.
6.将6位志愿者分成4组,其中两个组各2人,另两个组各1人,分赴世博会的四个不同场馆服务,不同的分配方案有( )种
A.1080个 B.1280 C.2160个 D.4320
7.某程序框图如右图所示,若输出的S=57,则判断框内填( )
A、k4? B、k5? C、k6? D、k7?
已知a>0,x、y满足约束条件
若z=2x+y的最小值为1,则a=( )
A.2 B. 1 C. D.
9.在矩形中,,若向该矩形内随投一点,那么使得与的面积都不小于2的概率为( )
A. B. C. D.
10.设m,n为正实数,若直线(m+1)x+(n+1)y-4=0与圆x2+y2-4x-4y+4=0相切,则mn( )
A.有最小值1+,无最大值 B.有最小值3-2,最大值3+2
C.有最大值3+2,无最小值 D.有最小值3+2,无最大值
11.已知函数,若,使得成立,则实数的取值范围是( )
A. B. C. D.
12.已知函数满足,当时,;当时,,若函数在上有五个零点,则的最小值为( )
A. B. C. D.
第Ⅱ卷
二.填空题:本大题共四小题,每小题5分,共20分。
13.△ABC中,a、b是它的两边,S是△ABC的面积,若,则△ABC的形状为
14.设的展开式中的常数项为-16,则 .
15.一个空间几何体的三视图(单位:)如图所示,则该几何体的体积为 .
16..已知数列 ,。满足条件
“”的数列个数为
三. 解答题:本大题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.(本小题满分10分)已知且,求函数的最大值和最小值.
18(本小题满分12分).在△ABC中,2cos2A+3=4cosA. (1)求角A的大小;(2)求△ABC的周长L的取值范围.
19. (本小题满分12分)上饶某中学一研究性学习小组早晨在校门口询问调查同学的体重,对来校同学依次每5人抽取一人询问体重,共抽取40位同学,将他们的体重(k分成六段: , , , , , 统计后得到如图的频率分布直方图.
(1)此研究性学习小组在采样中,用到的是什么抽样方法?并求这40位同学体重的众数和中位数的估计值.
(2)从体重在的同学中任意抽取3位,求体重在,内都有同学的概率.
20. (本小题满分12分)如图,在四棱锥中,是正方形,平面,, 分别是的中点.
(1)求证:平面平面;
(2)证明平面平面,并求出到平面的距离.
21.(本小题满分12分)在平面直角坐标系中,曲线与坐标轴的交点都在圆上
(Ⅰ)求圆的方程;
(Ⅱ)若圆与直线交与两点,且,求的值
22(本小题满分12分).已知数列满足,且.
(1)证明:数列为等比数列;
(2)设,记数列的前项和为,若对任意的,恒成立,求的取值范围.
高二数学(理)试卷答案及评分标准(自主班)
一、选择题:共12小题,每小题5分,满分60分.
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
B
A
C
A
A
B
C
D
D
B
A
二、填空题:共4小题,每小题5分,共20分.
13. 等腰直角三角形. 14. -1 ; 15.; 16. 233
17.(本小题满分10分)
解:由得,即 …………………4分
. …………………8分
当,当 …………………10分
18.(本小题满分12分)
(1)因为2cos2A+3=4cosA,所以2cos2A+=2cosA,
所以4cos2A-4cosA+1=0,所以cosA=,又因为0
所以(sinB+sinC).
因为B+C=,所以
又因为0
解(1)系统抽样,57.5, 57.5; ……………………………6分
(2)
……………………12分
(本小题满分12分)
(1)分别是线段的中点,所以,又为正方形,,
所以,
又平面,所以平面.
因为分别是线段的中点,所以,
又平面,所以,平面.
所以平面平面. ………………………………5分
(2)因为,,,所以平面,
又,所以平面,所以平面平面.
取中点,连接,则,平面即为平面,
在平面内,作,垂足为,则平面,
即为到平面的距离, ………………………10分
在三角形中,为中点,.………12分
(本小题满分12分)
(Ⅰ)曲线与轴交于点,与与轴交于点
因而圆心坐标为则有.
半径为,所以圆方程是. ………6分
(Ⅱ)解法一:设点满足
解得:.
.
解得,满足,
………………………………12分
解法二:设经过直线和圆的交点的圆的方程为
,若,则以AB为直径的圆过坐标原点
设上述圆就是这样的圆,则圆过原点,所以 ①
同时,该圆的圆心在直线上,化简得 ②
由①②求得。
(本小题满分12分)
(1)证明:因为,所以
即,则
从而数列是以6为首项,2为公比的等比数列 ………………4分
(2)解:由(1)知,即
所以………6分
当为偶数时,
………………8分
当为奇数时,
………………10分
当为偶数时,是递减的,此时当时,取最大值,则;
当为奇数时,是递增的,此时,则.
综上,的取值范围是. ……………12分
同课章节目录
