2019-2020学年度安徽省涡阳县新兴中心校第一学期九年级数学质量检测试卷(一)(word版,含答案)
文档属性
| 名称 | 2019-2020学年度安徽省涡阳县新兴中心校第一学期九年级数学质量检测试卷(一)(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 195.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 09:00:56 | ||
图片预览


文档简介
2019-2020学年度第一学期九年级质量检测试卷(一)
数学(沪科版)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共6页.
3.请务必在“答题卷”上答题,在“试题卷”上.答题是无效的.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10题,每题4分,共40分)
1.下列函数是二次函数的是( )
A.y=ax2+bx +c B.y=2x2-(1-2x)2 C.y =-x2 D.y=x2-+1
2.下列反比例函数中,图象经过点(1,-1)的是( )
A. B. C. D.
3.抛物线y =-2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(4,3) C.(-3,4) D.(4,-3)
4.已知抛物线y =ax2-2x+1的对称轴是直线x =1,a的值是( )
A.1 B.2 C.-1 D.-2
5.对于反比例函数,下列说法不正确的是( )
A.点(一2,-1)在它的图象上 B.它的图象在第一、三象限
C.当x>0时,y>0 D.y随x的增大而增大
6.如图,已知抛物线y =ax2+bx+c与x轴的一个交点为A(1,0),对称轴为直线x =-1,则方程ax2+bx+c =0的解是( )
A.x1 =-3,x2 =1
B.x1 =3,x2 =1
C.x =-3
D.x =-2
7.二次函数y =ax2+bx+2的图象经过点(1,0),则代数式2-a-b的值为( )
A.-3 B.0 C.4 D.-4
8.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形,它们分别是△P1A1O、△P2A2O、△P3A30,设它们的面积分别是S1、S2、S3,则( )
A.S1<S2<S3
B.S2<S1<S3
C.S3<S1<S2
D.S1=S2 =S3
9.某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m加设一根不锈钢支柱,防护栏的最高点距护栏底部 0.5m(如图),则这条护栏需要不锈钢支柱总长度至少为( )
A.50m
B.100m
C.120m
D.160m
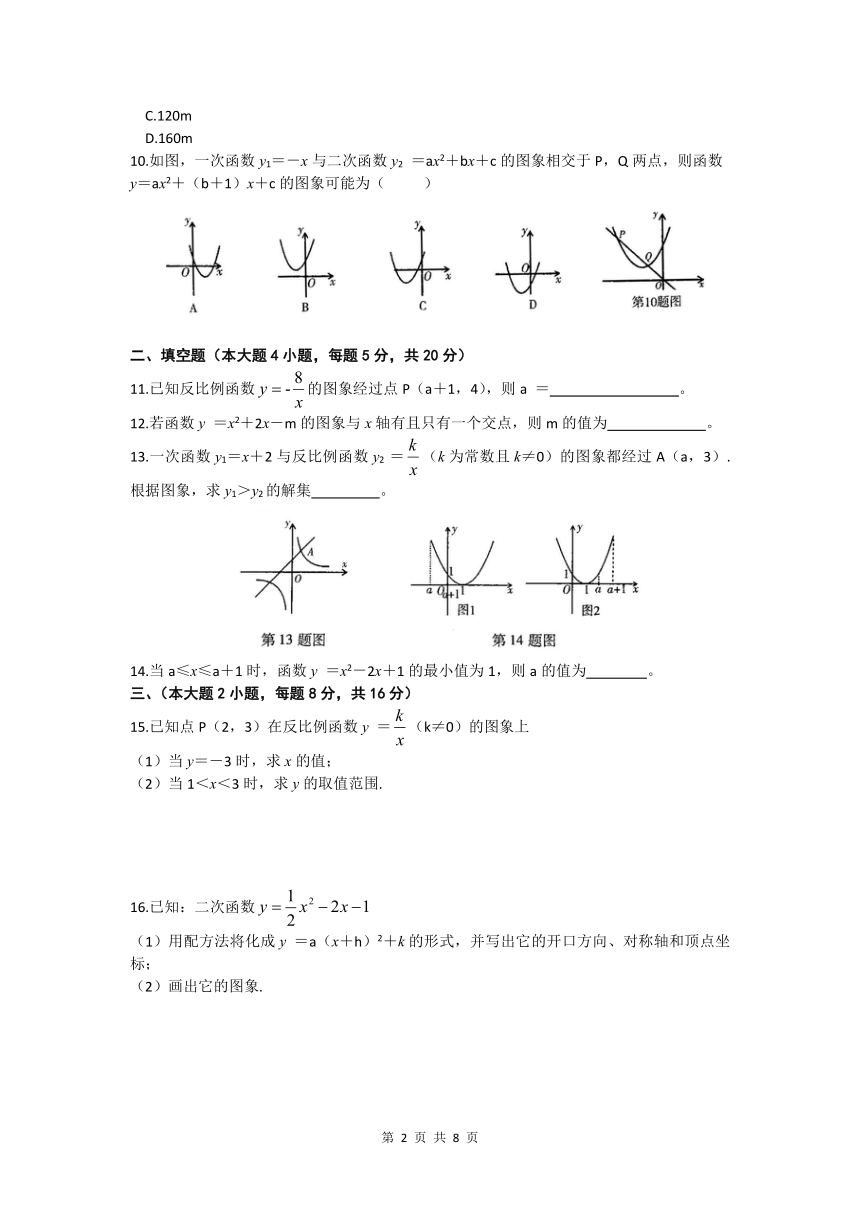
10.如图,一次函数y1=-x与二次函数y2 =ax2+bx+c的图象相交于P,Q两点,则函数
y=ax2+(b+1)x+c的图象可能为( )
二、填空题(本大题4小题,每题5分,共20分)
11.已知反比例函数的图象经过点P(a+1,4),则a = 。
12.若函数y =x2+2x-m的图象与x轴有且只有一个交点,则m的值为 。
13.一次函数y1=x+2与反比例函数y2 =(k为常数且k≠0)的图象都经过A(a,3).根据图象,求y1>y2的解集 。
14.当a≤x≤a+1时,函数y =x2-2x+1的最小值为1,则a的值为 。
三、(本大题2小题,每题8分,共16分)
15.已知点P(2,3)在反比例函数y =(k≠0)的图象上
(1)当y=-3时,求x的值;
(2)当1<x<3时,求y的取值范围.
16.已知:二次函数
(1)用配方法将化成y =a(x+h)2+k的形式,并写出它的开口方向、对称轴和顶点坐标;
(2)画出它的图象.
四、(本大题2小题,每题8分,共16分)
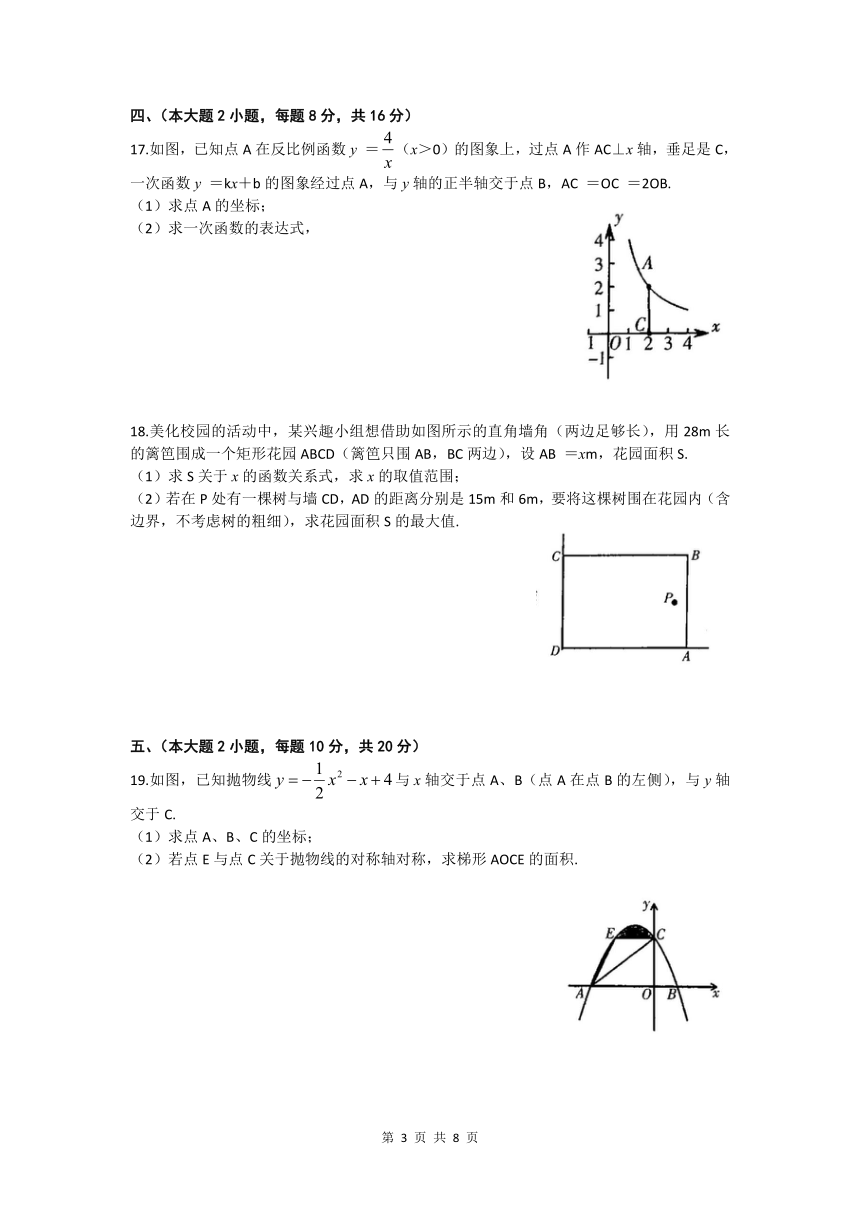
17.如图,已知点A在反比例函数y =(x>0)的图象上,过点A作AC⊥x轴,垂足是C,一次函数y =kx+b的图象经过点A,与y轴的正半轴交于点B,AC =OC =2OB.
(1)求点A的坐标;
(2)求一次函数的表达式,
18.美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB =xm,花园面积S.
(1)求S关于x的函数关系式,求x的取值范围;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
五、(本大题2小题,每题10分,共20分)
19.如图,已知抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
(1)求点A、B、C的坐标;
(2)若点E与点C关于抛物线的对称轴对称,求梯形AOCE的面积.
20.如图,已知一次函数y1=kx+b与反比例函数y2 =的图象在第一、第三象限分别交于
A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较线段AD、BC大小,并说明理由.
六、(本题12分)
21.已知关于x的二次函数y =-x2+(k-2)x+k+1.
(1)求证:该函数的图象与x轴一定有两个交点;
(2)当k =1时,设该函数的图象与x轴的交点为A、B(A在B的左侧),与y轴的交点为C,点P为其图象的对称轴上一动点,是否存在点P,使BP+CP最小,若存在,求出点P
的坐标.
七、(本题12分)
22.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间
为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式;
(2)方方上午8点驾驶小汽车从A地出发
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶
速度v的范围;
②方方能否在当天11点30分前到达B地?说明理由.
八、(本题14分)
23.草莓进入采摘旺季,某公司以3万元/吨的价格向农户收购了20吨草莓,分拣出甲类草莓x吨,其余为乙类草莓,甲类草莓包装后直接销售,乙类草莓深加工后再销售.甲类草莓的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y =-m+14(2≤m≤8),乙类草莓深加工(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系为S =3n+12,平均销售价格为9万元/吨。
(1)请直接写出该公司购买和包装甲类草莓所需资金: 万元.购买和加工乙类草
莓所需资金: 万元.
(2)若该公司将这20吨草莓全部售出,获得的毛利润为w万元.
(毛利润 =销售总收入-经营成本)
①求出w关于x的函数关系式;
②该公司的最小毛利润是多少?
2019-2020学年度第一学期九年级质量检测试卷(一)参考答案
数学(沪科版)
1—5.CBAAD 6—10.ACDDC
11.-3 12. -1 13.x>l或-3<x<0
14.a=2或a=-1
15.【答案】(1)∵点P(2,3)在反比例函数y=(k≠0)的图象上,
∴k=6,即y=,当y=-3时,-3==2,解得,x=-2;
(2)当x=1时,y=;当x=3时,y==2;又当∵1﹤x﹤3时,y随x的增大面减小,
∴y的取值范围2﹤x﹤6.
16.【答案】
(1)y=x2-2x-1=(x2-4x)-1=(x2-4x+4-4)-1
=(x-2)2-3,
∴开口方向向上,对称轴为x=2,顶点坐标(2,-3)
(2)二次函数y=x2-2x一1的图象如图所示
17.【答案](1)∵点A在反比例函数y=(x>0)的图象上,AC⊥x轴,AC=OC,
∴AC·OC=4,.AC=0C=2,
∴点A的坐标为(2,2).
(2)∵AC=OC=20B,∴OB=1,所以B的坐标为(0,1)
当B的坐标为(0,1),则有
解得,k=,b=1.即y=x+1,
∴一次函数的表达式为y=x+1,
18.(1)由题意可得出:S=x(28-x)=-x2+28x,求x的取值范曲0﹤x﹤28;
(2)S=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,∴x的取值范围6≤x≤13
∵-1﹤0,∴当6≤x≤13时.S随x的增大而增大,
∴x=13时,S取到最大值为:S=-(13-14)2+196=195,
答:花园面积S的最大值为195平方米.
19.{答案】解:(1)当y=0时,-x+4=0,解得x1=-4,x2=2,
∴A(-4,0),B(2,0),当x=0时,y=4,∴C(0,4);
(2)y=﹣x+4=(x+1)2+5,∴抛物线y=﹣x+4的对称轴是直线x=-1,
∴E的坐标为(-2,4),S梯形AOCE=,
20.(1)将A(3,4)代人y2=,可得m=12,∴y2=
将B(a,-2)代人y2=中,可得a=-6,∴B(-6,-2)
将A(3,4),B(-6,-2)分别代人y1=kx+b中,可得
解得k=,b=2,∴y1=+2,y2=
(2)AD=BC,理由为:
∵C,D是y=+2与y轴,x轴的交点,∴C(0,2),D(-3,0)
∴AD=2,BC=2,∴AD=BC.
21.解:(1)∵△=(k-2)2-4×(-1)(k+1)=k2+8,
∴该函数的图象与x轴一定有两个交点;
(2)当k=1时,y=-x2-x+2=(x+)2+
即此函数图象的对称轴为直线x=-2,当y=0时,-x2-x+2=0,解得:x1=1,x2=-2,
即A(-2,0),B(1,0);当x=0时,y=2,即C(0,2);
∵A、B关于直线x=对称,
∴点P为直线x=与AC交点时,BP+CP最小,设直线AC对应的解析式为:y=kx+b,
,解得k=1,b=2,即y=x+2,当x=时,y=
∴点的坐标为(,)
22.【答案】(1)根据题意,得vt=480,所以,因为480>0,
所以当v≤120时,t≥4.
综上,v关于t的函数表达式为(t≥4)
(2)①根据题意,得4.8≤t≤6,当t=4.8时,v=100;当t=6时,v=80.
∴小汽车行驶速度v的范围是80≤v≤100;
②方方不能在11点30分前到达B地.理由如下:
法一:若方方要在11点30分前到达B地,则t﹤3.5,
所以v>>120,所以方方不能在11点30分前到达B地;
法二:方方按最快的速度行驶,那么v=120,当v=120时,可得t==4,8+4=12,
∴方方最早也要在12点才能到达,不能在当天11点30分前到达B地,
23.【答案】解:(1)甲方式购买和包装x吨农产品所需资金为:4x万元;
乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
故答案为:4x,(132-6x);
(2)①w甲=x(-x+14)-x=-x2+13x;w乙=9(20-x)-[12+3(20-x)]=108-6x
∴W=w甲+w乙﹣3×20=(-x2+13x)+(108﹣6x)·60=-x2+7x+48;
②∵当2≤x≤8时,w=-x2+7x+48=-(x﹣3.5)2+60.25,
∴当x=8时,w最小=40;故当x=8时,利润最小为40万元.
数学(沪科版)
注意事项:
1.你拿到的试卷满分为150分,考试时间为120分钟
2.本试卷包括“试题卷”和“答题卷”两部分.“试题卷”共4页,“答题卷”共6页.
3.请务必在“答题卷”上答题,在“试题卷”上.答题是无效的.
4.考试结束后,请将“试题卷”和“答题卷”一并交回.
一、选择题(本大题共10题,每题4分,共40分)
1.下列函数是二次函数的是( )
A.y=ax2+bx +c B.y=2x2-(1-2x)2 C.y =-x2 D.y=x2-+1
2.下列反比例函数中,图象经过点(1,-1)的是( )
A. B. C. D.
3.抛物线y =-2(x-3)2+4的顶点坐标是( )
A.(3,4) B.(4,3) C.(-3,4) D.(4,-3)
4.已知抛物线y =ax2-2x+1的对称轴是直线x =1,a的值是( )
A.1 B.2 C.-1 D.-2
5.对于反比例函数,下列说法不正确的是( )
A.点(一2,-1)在它的图象上 B.它的图象在第一、三象限
C.当x>0时,y>0 D.y随x的增大而增大
6.如图,已知抛物线y =ax2+bx+c与x轴的一个交点为A(1,0),对称轴为直线x =-1,则方程ax2+bx+c =0的解是( )
A.x1 =-3,x2 =1
B.x1 =3,x2 =1
C.x =-3
D.x =-2
7.二次函数y =ax2+bx+2的图象经过点(1,0),则代数式2-a-b的值为( )
A.-3 B.0 C.4 D.-4
8.如图,P1、P2、P3是双曲线上的三点,过这三点分别作y轴的垂线,得到三个三角形,它们分别是△P1A1O、△P2A2O、△P3A30,设它们的面积分别是S1、S2、S3,则( )
A.S1<S2<S3
B.S2<S1<S3
C.S3<S1<S2
D.S1=S2 =S3
9.某学校院墙上部是由100段形状相同的抛物线形护栏组成的,为了牢固起见,每段护栏需要间隔0.4m加设一根不锈钢支柱,防护栏的最高点距护栏底部 0.5m(如图),则这条护栏需要不锈钢支柱总长度至少为( )
A.50m
B.100m
C.120m
D.160m
10.如图,一次函数y1=-x与二次函数y2 =ax2+bx+c的图象相交于P,Q两点,则函数
y=ax2+(b+1)x+c的图象可能为( )
二、填空题(本大题4小题,每题5分,共20分)
11.已知反比例函数的图象经过点P(a+1,4),则a = 。
12.若函数y =x2+2x-m的图象与x轴有且只有一个交点,则m的值为 。
13.一次函数y1=x+2与反比例函数y2 =(k为常数且k≠0)的图象都经过A(a,3).根据图象,求y1>y2的解集 。
14.当a≤x≤a+1时,函数y =x2-2x+1的最小值为1,则a的值为 。
三、(本大题2小题,每题8分,共16分)
15.已知点P(2,3)在反比例函数y =(k≠0)的图象上
(1)当y=-3时,求x的值;
(2)当1<x<3时,求y的取值范围.
16.已知:二次函数
(1)用配方法将化成y =a(x+h)2+k的形式,并写出它的开口方向、对称轴和顶点坐标;
(2)画出它的图象.
四、(本大题2小题,每题8分,共16分)
17.如图,已知点A在反比例函数y =(x>0)的图象上,过点A作AC⊥x轴,垂足是C,一次函数y =kx+b的图象经过点A,与y轴的正半轴交于点B,AC =OC =2OB.
(1)求点A的坐标;
(2)求一次函数的表达式,
18.美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB =xm,花园面积S.
(1)求S关于x的函数关系式,求x的取值范围;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
五、(本大题2小题,每题10分,共20分)
19.如图,已知抛物线与x轴交于点A、B(点A在点B的左侧),与y轴交于C.
(1)求点A、B、C的坐标;
(2)若点E与点C关于抛物线的对称轴对称,求梯形AOCE的面积.
20.如图,已知一次函数y1=kx+b与反比例函数y2 =的图象在第一、第三象限分别交于
A(3,4),B(a,-2)两点,直线AB与y轴,x轴分别交于C,D两点.
(1)求一次函数和反比例函数的解析式;
(2)比较线段AD、BC大小,并说明理由.
六、(本题12分)
21.已知关于x的二次函数y =-x2+(k-2)x+k+1.
(1)求证:该函数的图象与x轴一定有两个交点;
(2)当k =1时,设该函数的图象与x轴的交点为A、B(A在B的左侧),与y轴的交点为C,点P为其图象的对称轴上一动点,是否存在点P,使BP+CP最小,若存在,求出点P
的坐标.
七、(本题12分)
22.方方驾驶小汽车匀速地从A地行驶到B地,行驶里程为480千米,设小汽车的行驶时间
为t(单位:小时),行驶速度为v(单位:千米/小时),且全程速度限定为不超过120千米/小时.
(1)求v关于t的函数表达式;
(2)方方上午8点驾驶小汽车从A地出发
①方方需在当天12点48分至14点(含12点48分和14点)间到达B地,求小汽车行驶
速度v的范围;
②方方能否在当天11点30分前到达B地?说明理由.
八、(本题14分)
23.草莓进入采摘旺季,某公司以3万元/吨的价格向农户收购了20吨草莓,分拣出甲类草莓x吨,其余为乙类草莓,甲类草莓包装后直接销售,乙类草莓深加工后再销售.甲类草莓的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y =-m+14(2≤m≤8),乙类草莓深加工(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系为S =3n+12,平均销售价格为9万元/吨。
(1)请直接写出该公司购买和包装甲类草莓所需资金: 万元.购买和加工乙类草
莓所需资金: 万元.
(2)若该公司将这20吨草莓全部售出,获得的毛利润为w万元.
(毛利润 =销售总收入-经营成本)
①求出w关于x的函数关系式;
②该公司的最小毛利润是多少?
2019-2020学年度第一学期九年级质量检测试卷(一)参考答案
数学(沪科版)
1—5.CBAAD 6—10.ACDDC
11.-3 12. -1 13.x>l或-3<x<0
14.a=2或a=-1
15.【答案】(1)∵点P(2,3)在反比例函数y=(k≠0)的图象上,
∴k=6,即y=,当y=-3时,-3==2,解得,x=-2;
(2)当x=1时,y=;当x=3时,y==2;又当∵1﹤x﹤3时,y随x的增大面减小,
∴y的取值范围2﹤x﹤6.
16.【答案】
(1)y=x2-2x-1=(x2-4x)-1=(x2-4x+4-4)-1
=(x-2)2-3,
∴开口方向向上,对称轴为x=2,顶点坐标(2,-3)
(2)二次函数y=x2-2x一1的图象如图所示
17.【答案](1)∵点A在反比例函数y=(x>0)的图象上,AC⊥x轴,AC=OC,
∴AC·OC=4,.AC=0C=2,
∴点A的坐标为(2,2).
(2)∵AC=OC=20B,∴OB=1,所以B的坐标为(0,1)
当B的坐标为(0,1),则有
解得,k=,b=1.即y=x+1,
∴一次函数的表达式为y=x+1,
18.(1)由题意可得出:S=x(28-x)=-x2+28x,求x的取值范曲0﹤x﹤28;
(2)S=-x2+28x=-(x-14)2+196,
∵在P处有一棵树与墙CD,AD的距离分别是15m和6m,∴x的取值范围6≤x≤13
∵-1﹤0,∴当6≤x≤13时.S随x的增大而增大,
∴x=13时,S取到最大值为:S=-(13-14)2+196=195,
答:花园面积S的最大值为195平方米.
19.{答案】解:(1)当y=0时,-x+4=0,解得x1=-4,x2=2,
∴A(-4,0),B(2,0),当x=0时,y=4,∴C(0,4);
(2)y=﹣x+4=(x+1)2+5,∴抛物线y=﹣x+4的对称轴是直线x=-1,
∴E的坐标为(-2,4),S梯形AOCE=,
20.(1)将A(3,4)代人y2=,可得m=12,∴y2=
将B(a,-2)代人y2=中,可得a=-6,∴B(-6,-2)
将A(3,4),B(-6,-2)分别代人y1=kx+b中,可得
解得k=,b=2,∴y1=+2,y2=
(2)AD=BC,理由为:
∵C,D是y=+2与y轴,x轴的交点,∴C(0,2),D(-3,0)
∴AD=2,BC=2,∴AD=BC.
21.解:(1)∵△=(k-2)2-4×(-1)(k+1)=k2+8,
∴该函数的图象与x轴一定有两个交点;
(2)当k=1时,y=-x2-x+2=(x+)2+
即此函数图象的对称轴为直线x=-2,当y=0时,-x2-x+2=0,解得:x1=1,x2=-2,
即A(-2,0),B(1,0);当x=0时,y=2,即C(0,2);
∵A、B关于直线x=对称,
∴点P为直线x=与AC交点时,BP+CP最小,设直线AC对应的解析式为:y=kx+b,
,解得k=1,b=2,即y=x+2,当x=时,y=
∴点的坐标为(,)
22.【答案】(1)根据题意,得vt=480,所以,因为480>0,
所以当v≤120时,t≥4.
综上,v关于t的函数表达式为(t≥4)
(2)①根据题意,得4.8≤t≤6,当t=4.8时,v=100;当t=6时,v=80.
∴小汽车行驶速度v的范围是80≤v≤100;
②方方不能在11点30分前到达B地.理由如下:
法一:若方方要在11点30分前到达B地,则t﹤3.5,
所以v>>120,所以方方不能在11点30分前到达B地;
法二:方方按最快的速度行驶,那么v=120,当v=120时,可得t==4,8+4=12,
∴方方最早也要在12点才能到达,不能在当天11点30分前到达B地,
23.【答案】解:(1)甲方式购买和包装x吨农产品所需资金为:4x万元;
乙方式购买和加工其余农产品所需资金为:3(20-x)+3(20-x)+12=(132-6x)万元;
故答案为:4x,(132-6x);
(2)①w甲=x(-x+14)-x=-x2+13x;w乙=9(20-x)-[12+3(20-x)]=108-6x
∴W=w甲+w乙﹣3×20=(-x2+13x)+(108﹣6x)·60=-x2+7x+48;
②∵当2≤x≤8时,w=-x2+7x+48=-(x﹣3.5)2+60.25,
∴当x=8时,w最小=40;故当x=8时,利润最小为40万元.
同课章节目录
