青岛版九年级数学上册课件2.5 解直角三角形的应用(20张PPT)
文档属性
| 名称 | 青岛版九年级数学上册课件2.5 解直角三角形的应用(20张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 00:00:00 | ||
图片预览








文档简介
课件20张PPT。教学课件
数学 九年级上册 青岛版
第2章 解直角三角形
2.5 解直角三角形的应用教学重点难点重点:善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
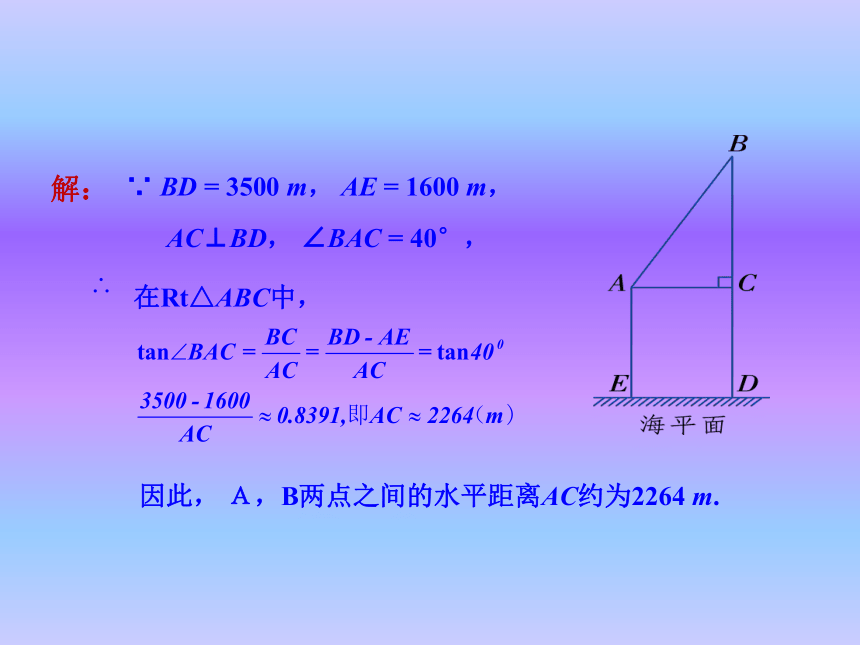
难点:根据实际问题构造合适的直角三角形.新课引入 在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.动脑筋 某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地——海拔为3 500 m的山峰顶点B处的水平距离. 他能想出一个可行的办法吗? 如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.∵ BD = 3500 m, AE = 1600 m,
AC⊥BD, ∠BAC = 40°, 因此, A,B两点之间的水平距离AC约为2264 m.解:例题探究例1 如图所示, 在离上海东方明珠塔底部1 000 m 的A 处, 用仪器测得塔顶的仰角∠BAC 为25°, 仪器距地面高AE 为1.7 m. 求上海东方明珠塔的高度BD(结果精确到 1 m).分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.解:如图,在Rt△ABC中,∠BAC =25°,AC =100m,答:上海东方明珠塔的高度BD为468 m.如图,从山脚到山顶有两条路 AB 与BD,问哪条路比较陡?探究右边的路BD 陡些.如何用数量来刻画哪条路陡呢?如图,在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m. 如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上. 已知在灯塔C的四周30km内有暗礁.问这艘船继续向东航行是否安全?
因此,该船能继续安全地向东航行.课堂练习 1.如图,某厂家新开发的一种电动车的大灯A射出的光线AB,AC与地面MN所形成的夹角∠ABN, ∠ACN分别为8°和15°,大灯A与地面的距离为1m,求该车大灯照亮地面的宽度BC(不考虑其他因素,结果精确到0.1m).课堂小结
数学 九年级上册 青岛版
第2章 解直角三角形
2.5 解直角三角形的应用教学重点难点重点:善于将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
难点:根据实际问题构造合适的直角三角形.新课引入 在日常生活中,我们经常会碰到一些与直角三角形有关的实际问题.对于这些问题,我们可以用所学的解直角三角形的知识来加以解决.动脑筋 某探险者某天到达如图所示的点A 处时,他准备估算出离他的目的地——海拔为3 500 m的山峰顶点B处的水平距离. 他能想出一个可行的办法吗? 如右图所示,BD表示点B的海拔,AE 表示点A 的海拔,AC⊥BD,垂足为点C. 先测量出海拔AE,再测出仰角∠BAC,然后用锐角三角函数的知识就可求出A,B两点之间的水平距离AC.∵ BD = 3500 m, AE = 1600 m,
AC⊥BD, ∠BAC = 40°, 因此, A,B两点之间的水平距离AC约为2264 m.解:例题探究例1 如图所示, 在离上海东方明珠塔底部1 000 m 的A 处, 用仪器测得塔顶的仰角∠BAC 为25°, 仪器距地面高AE 为1.7 m. 求上海东方明珠塔的高度BD(结果精确到 1 m).分析:在直角三角形中,已知一角和它的邻边,求对边利用该角的正切即可.解:如图,在Rt△ABC中,∠BAC =25°,AC =100m,答:上海东方明珠塔的高度BD为468 m.如图,从山脚到山顶有两条路 AB 与BD,问哪条路比较陡?探究右边的路BD 陡些.如何用数量来刻画哪条路陡呢?如图,在Rt△ABC中,∠B=90°,∠A=26.57°,AC=240m,答:这座山坡的坡角约为26.57°,小刚上升了约107.3 m. 如图,一艘船以40km/h的速度向正东航行,在A处测得灯塔C在北偏东60°方向上,继续航行1h到达B处,这时测得灯塔C在北偏东30°方向上. 已知在灯塔C的四周30km内有暗礁.问这艘船继续向东航行是否安全?
因此,该船能继续安全地向东航行.课堂练习 1.如图,某厂家新开发的一种电动车的大灯A射出的光线AB,AC与地面MN所形成的夹角∠ABN, ∠ACN分别为8°和15°,大灯A与地面的距离为1m,求该车大灯照亮地面的宽度BC(不考虑其他因素,结果精确到0.1m).课堂小结
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
