23.1.2 平行线分线段成比例 同步练习(含解析)
文档属性
| 名称 | 23.1.2 平行线分线段成比例 同步练习(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 18:39:52 | ||
图片预览



文档简介
初中数学华师大版九年级上学期 第23章 23.1.2 平行线分线段成比例
一、单选题
1.如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则(??? )21cnjy.com
A.??????????????B.??????????????C.??????????????D.?
2.如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为(??? ) 2·1·c·n·j·y
A.?1???????????????????????????????????????????B.????????????????????????????????????????????C.?2???????????????????????????????????????????D.?4
3.如图,在 中, , , , ,则 的长为(?? )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
4.如图所示,已知AB∥CD∥EF,那么下列结论正确的是(?? )
A.??????????????????????B.?= ?????????????????????C.?= ?????????????????????D.?=
5.哥哥身高 米,在地面上的影子长是 米,同一时间测得弟弟的影子长 米,则弟弟身高是( ???)
A.?1.44米????????????????????????????????B.?1.52米????????????????????????????????C.?1.96米????????????????????????????????D.?2.25米
6.如图l1∥l2∥l3 , 若 ,DF=10,则DE=(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
二、填空题
7.如图,在△ABC中,AB=5,AC=4,若进行一下操作,在边BC上从左到右一次取点D1、D2、D3、D4…;过点D1作AB、AC的平行线分别交于AC、AB与点E1、F1;过点D2作AB、AC的平行线分别交于AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交于AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2019E2019)+5(D1F1+D2F2+…+D2019F2019)=________.【来源:21·世纪·教育·网】
8.如图, ,直线a、b与 、 、 分别相交于点A、B、C和点D、E、F.若 , , ,则 ________. www-2-1-cnjy-com
9.如图L4 , L5被一组平行线L1 , L2 , L3所截,显然三条平行线不是等距的,若 ,则 为________. 21*cnjy*com
10.在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为________. 【来源:21cnj*y.co*m】
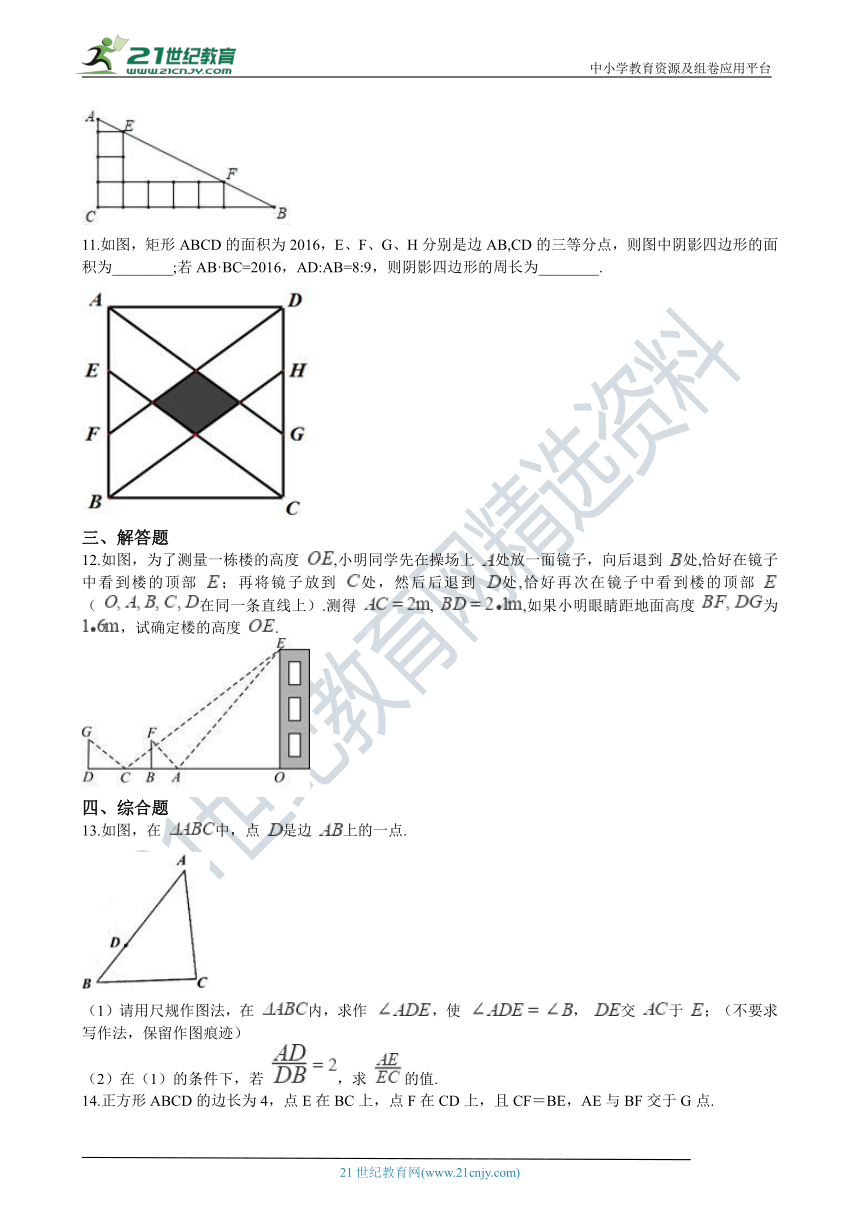
11.如图,矩形ABCD的面积为2016,E、F、G、H分别是边AB,CD的三等分点,则图中阴影四边形的面积为________;若AB·BC=2016,AD:AB=8:9,则阴影四边形的周长为________.【版权所有:21教育】
三、解答题
12.如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 . 21教育名师原创作品
四、综合题
13.如图,在 中,点 是边 上的一点.
(1)请用尺规作图法,在 内,求作 ,使 , 交 于 ;(不要求写作法,保留作图痕迹) 21*cnjy*com
(2)在(1)的条件下,若 ,求 的值.
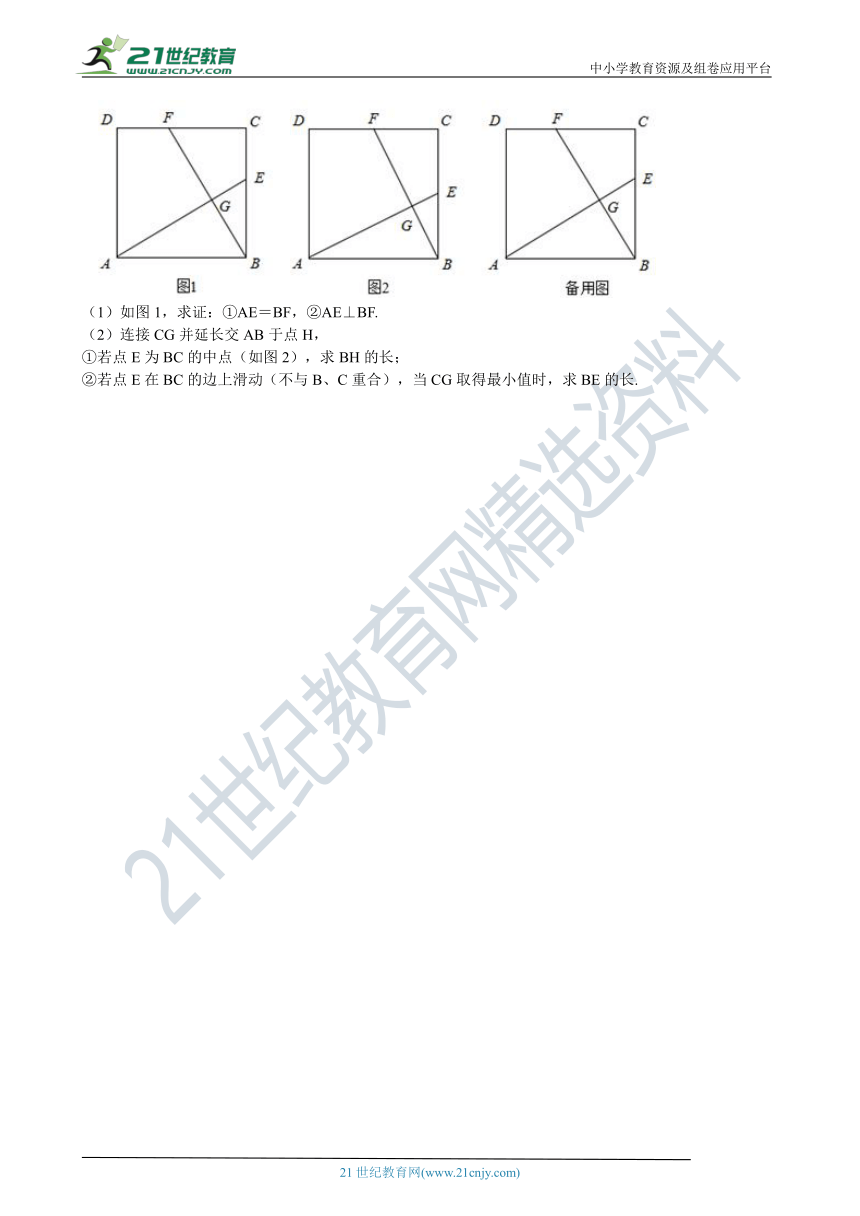
14.正方形ABCD的边长为4,点E在BC上,点F在CD上,且CF=BE,AE与BF交于G点.
(1)如图1,求证:①AE=BF,②AE⊥BF.
(2)连接CG并延长交AB于点H,
①若点E为BC的中点(如图2),求BH的长;
②若点E在BC的边上滑动(不与B、C重合),当CG取得最小值时,求BE的长.
答案解析部分
一、单选题
1. C
分析:解:A.∵DE∥BC,
∴ , ,
∴ , ,
∵ ≠ ,
∴ ≠ ,
故错误,A不符合题意;
B.∵DE∥BC,
∴ , ,
∴ , ,
∵ ≠ ,
∴ ≠ ,
故错误,B不符合题意;
C.∵DE∥BC,
∴ , ,
∴ = ,
故正确,C符合题意;
D.∵DE∥BC,
∴ , ,
∴ = ,
即 = ,
故错误,D不符合题意;
故答案为:C.
【分析】根据平行线截线段成比例逐一分析即可判断对错,从而可得答案.
2. C
分析:解:如图,延长FH交AB于点M,
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故答案为:C。
【分析】如图,延长FH交AB于点M,根据线段之间的关系可以得出AE:AB=AG:AC,CF:CD=CH:CA,根据平行线分线段成比例定理的逆用得出EG//BC,FH//AD,根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出△AEG∽△ABC,△CFH∽△CDA,根据相似三角形对应边成比例得出EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,根据矩形的性质进而即可得出EG=2,HF=2,根据一组对边平行且相等的四边形是平行四边形判断出四边形EHFG为平行四边形,进而根据平行四边形面积的计算方法即可算出答案。www.21-cn-jy.com
3. C
分析:∵ ,
∴ ,即 ,
∴ ,
∴ .
故答案为:C .
【分析】根据平行线分线段成比例定理,可得, 代入数据求出AE的长,由AC=AE+EC求出AC的长即可.2-1-c-n-j-y
4. A
分析:解:∵AB∥CD∥EF,
∴ = ,
∴A符合题意,
故答案为:A.
【分析】根据平行线分线段成比例定理可得:。
5. A
分析:解:设弟弟的身高是xm
则
解得:x=1.44
故答案为:A.
【分析】设弟弟的身高是xm,根据同一时刻,同一地点,同一平面不同物体的高度与影长成比例列出方程,求解即可。【出处:21教育名师】
6. B
分析:解:由题意得 ,则DE= ,
故答案为:B.
【分析】根据平行线分线段成比例定理得出, 根据比例式即可求出答案。
二、填空题
7. 40380
分析:∵D1E1∥AB? ?D1F1∥AC
∴ ??
∵AB=5?? AC=4
∴ ??? ??
∴
∴4D1E+5D1F=20?
有2019组,即2019×20=40380
故答案为: 40380 。 【分析】根据平行线分线段成比例定理得出 ?? 然后根据等式的性质,将两个等式相加即可得出4D1E+5D1F=20 ,进而利用乘法分配律及加法结合律可知整个代数式共有2019组20,从而根据有理数的乘法法则即可算出答案。
8. 4
分析:解:∵ ,
∴ ,
又 , , ,
∴ 。
故答案为:4。
【分析】根据平行线分线段成比例定理得出 ,由比例式即可建立方程,求解即可得出EF的长。
9.
分析:解:∵L1∥L2∥L3 ,
,
故答案为: .
【分析】根据平行线分线段成比例定理解答即可.
10.
分析:解:如图,设AH=x,GB=y,
∵EH∥BC,
,
∵FG∥AC,
,
由①②可得x= ,y=2,
∴AC= ,BC=7,
∴S△ABC= ,
故答案为 .
【分析】设AH=x,GB=y,再利用平行线分线段成比例定理,由EH∥BC,FG∥AC,可得出对应线段成比例,建立关于x,y的方程组,解方程组求出x,y的值,从而可求出AC,BC的值,然后利用直角三角形的面积公式就可求出△ABC的面积。21·cn·jy·com
11. 168;20
分析:解:连接KI,连接JL,并延长交AB、CD于点M、N,连接FG ∵矩形ABCD ∴AB∥CD ∵ E、F、G、H分别是边AB,CD的三等分点 ∴AE=AB,CG=CD, ∴AE=CG,AE∥CG ∴△AECG是平行四边形 ∴AG∥CE 同理可证:DF∥BH ∴四边形IJKL是平行四边形 ∵AF=DG,AF∥DG,∠FAD=90° ∴四边形AFGD是矩形, ∴IA=ID=IG=IF ∵AI∥EJ ∴即IJ=FI 同理可证IL=GI ∴JL是△IFG的中位线 ∴JL=FG=BC ∴IJ=IL ∴四边形IJKL是菱形, ∴JL⊥IK, ∵IK=AE=AB ∴S菱形IJKL=IK·JL=×AB·BC=AB·BC=×2016=168; ∵AB·BC=2016,AD:AB=8:9 设AD=8x,AB=9x ∴72x2=2016 解之:x= ∴IK=AB=, JL=BC= ∴IO=JL=, LO=IK= 在Rt△ILO中,IL= ∴菱形IJKL的周长为:4×= 故答案为:168; 【分析】连接KI,连接JL,并延长交AB、CD于点M、N,连接FG,利用矩形的性质及已知E、F、G、H分别是边AB,CD的三等分点,易证△AECG是平行四边形,再证明四边形IJKL是平行四边形,四边形AFGD是矩形,利用平行线分线段成比例定理及三角形中位线定理,可证得IJ=IL,从而可证得四边形IJKL是菱形,再证明JL=BC,IK=AB,然后利用菱形的面积等于两对角线之积的一半,就可求出阴影部分的面积;由已知AB·BC=2016,AD:AB=8:9,设AD=8x,AB=9x,列方程求出x的值,从而可求出IO、LO的长,再利用勾股定理求出IL的长,然后利用菱形的性质,就可求出阴影部分的周长。
三、解答题
12. 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,??
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
【解析】【分析】根据光的反射定律作出相关光路图,因为GF∥AC,利用三角形相似分别列比例式。因为根据平面镜成像特点,像和物是等大的,找出有关相等的线段,进行一系列相关的等量代换,使关系式用用已知线段表示,代入已知数据,得出楼的高度。21·世纪*教育网
四、综合题
13. (1)解:如图所示;
(2)解:∵ ,
∴ .
∴ .
【解析】【分析】(1)利用尺规,依次找到角的对应点,画出角即可。 (2)根据两线平行、两角相等,可得到对应的边成比例,得到比值。21教育网
14. (1)证明:①∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=∠BCD=90°,
在△ABE和△BCF中, ,
∴△ABE≌△BCF(SAS),
∴AE=BF;
②由①得:△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AGB=90°,
∴AE⊥BF
(2)解:①如图2所示:
∵E为BC的中点,
∴CF=BE= BC=2,
∴BF ,
由(1)得:AE⊥BF,
∴∠BGE=∠ABE=90°,
∵∠BEG=∠AEB,
∴△BEG∽△AEB,
∴ ,
设GE=x,则BG=2x,
在Rt△BEG中,由勾股定理得:x2+(2x)2=22 ,
解得:x= ,
∴BG=2× ,
∵AB∥CD,
∴ ,即 ,
解得:BH= ;
②由(1)得:∠AGB=90°,
∴点G在以AB为直径的圆上,
设AB的中点为M,
由图形可知:当C、G、M在同一直线上时,CG为最小值,如图3所示:
∵AE⊥BF,
∴∠AGB=90°,
∴GM= AB=BM=2,
∵AB∥CD,
∴ =1,
∴CF=CG,
∵CF=BE,
∴CF=CG=BE,
设CF=CG=BE=a,则CM=a+2,
在Rt△BCM中,由勾股定理得:22+42=(a+2)2 ,
解得:a=2 ﹣2,即
当CG取得最小值时,BE的长为2 ﹣2.
【解析】【分析】(1)①由正方形的性质得出AB=BC,∠ABC=∠BCD=90°,结合已知用边角边可证△ABE≌△BCF,由全等三角形的性质即可求解; ②由①中放入全等三角形可得∠BAE=∠CBF,结合∠CBF+∠ABF=90°可证∠AGB=90°,由垂线的定义即可求解; (2)①由直角三角形的性质得CF=BE=BC,用勾股定理求得BF得值,由(1)的结论得:AE⊥BF,则∠BGE=∠ABE=90°,根据两个角对应相等的两个三角形相似可证△BEG∽△AEB,由相似三角形的性质可得比例式, 设GE=x,则BG=2x,在Rt△BEG中,由勾股定理得关于x的方程,解方程求得BG的值,由平行线分线段成比例定理得比例式, 将已知的线段代入比例式计算即可求得BH的长; ②由(1)的结论得:∠AGB=90°,根据点与圆的位置关系知:点G在以AB为直径的圆上,设AB的中点为M,当C、G、M在同一直线上时,CG为最小值,则GM=AB=BM,由平行线分线段成比例定理得比例式, 结合已知可得CF=CG=BE,设CF=CG=BE=a,则CM=a+2,在Rt△BCM中,由勾股定理得关于a的方程,解方程即可求解.21世纪教育网版权所有
一、单选题
1.如图,在△ABC中,点D,E分别在AB和AC边上,DE∥BC,M为BC边上一点(不与点B、C重合),连接AM交DE于点N,则(??? )21cnjy.com
A.??????????????B.??????????????C.??????????????D.?
2.如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为(??? ) 2·1·c·n·j·y
A.?1???????????????????????????????????????????B.????????????????????????????????????????????C.?2???????????????????????????????????????????D.?4
3.如图,在 中, , , , ,则 的长为(?? )
A.?6???????????????????????????????????????????B.?7???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
4.如图所示,已知AB∥CD∥EF,那么下列结论正确的是(?? )
A.??????????????????????B.?= ?????????????????????C.?= ?????????????????????D.?=
5.哥哥身高 米,在地面上的影子长是 米,同一时间测得弟弟的影子长 米,则弟弟身高是( ???)
A.?1.44米????????????????????????????????B.?1.52米????????????????????????????????C.?1.96米????????????????????????????????D.?2.25米
6.如图l1∥l2∥l3 , 若 ,DF=10,则DE=(?? )
A.?4???????????????????????????????????????????B.?6???????????????????????????????????????????C.?8???????????????????????????????????????????D.?9
二、填空题
7.如图,在△ABC中,AB=5,AC=4,若进行一下操作,在边BC上从左到右一次取点D1、D2、D3、D4…;过点D1作AB、AC的平行线分别交于AC、AB与点E1、F1;过点D2作AB、AC的平行线分别交于AC、AB于点E2、F2;过点D3作AB、AC的平行线分别交于AC、AB于点E3、F3…,则4(D1E1+D2E2+…+D2019E2019)+5(D1F1+D2F2+…+D2019F2019)=________.【来源:21·世纪·教育·网】
8.如图, ,直线a、b与 、 、 分别相交于点A、B、C和点D、E、F.若 , , ,则 ________. www-2-1-cnjy-com
9.如图L4 , L5被一组平行线L1 , L2 , L3所截,显然三条平行线不是等距的,若 ,则 为________. 21*cnjy*com
10.在Rt△ABC纸片上剪出7个如图所示的正方形,点E,F落在AB边上,每个正方形的边长为1,则Rt△ABC的面积为________. 【来源:21cnj*y.co*m】
11.如图,矩形ABCD的面积为2016,E、F、G、H分别是边AB,CD的三等分点,则图中阴影四边形的面积为________;若AB·BC=2016,AD:AB=8:9,则阴影四边形的周长为________.【版权所有:21教育】
三、解答题
12.如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 . 21教育名师原创作品
四、综合题
13.如图,在 中,点 是边 上的一点.
(1)请用尺规作图法,在 内,求作 ,使 , 交 于 ;(不要求写作法,保留作图痕迹) 21*cnjy*com
(2)在(1)的条件下,若 ,求 的值.
14.正方形ABCD的边长为4,点E在BC上,点F在CD上,且CF=BE,AE与BF交于G点.
(1)如图1,求证:①AE=BF,②AE⊥BF.
(2)连接CG并延长交AB于点H,
①若点E为BC的中点(如图2),求BH的长;
②若点E在BC的边上滑动(不与B、C重合),当CG取得最小值时,求BE的长.
答案解析部分
一、单选题
1. C
分析:解:A.∵DE∥BC,
∴ , ,
∴ , ,
∵ ≠ ,
∴ ≠ ,
故错误,A不符合题意;
B.∵DE∥BC,
∴ , ,
∴ , ,
∵ ≠ ,
∴ ≠ ,
故错误,B不符合题意;
C.∵DE∥BC,
∴ , ,
∴ = ,
故正确,C符合题意;
D.∵DE∥BC,
∴ , ,
∴ = ,
即 = ,
故错误,D不符合题意;
故答案为:C.
【分析】根据平行线截线段成比例逐一分析即可判断对错,从而可得答案.
2. C
分析:解:如图,延长FH交AB于点M,
∵BE=2AE,DF=2FC,AB=AE+BE,CD=CF+DF,
∴AE:AB=1:3,CF:CD=1:3,
又∵G、H分别是AC的三等分点,
∴AG:AC=CH:AC=1:3,
∴AE:AB=AG:AC,CF:CD=CH:CA,
∴EG//BC,FH//AD,
∴△AEG∽△ABC,△CFH∽△CDA,BM:AB=CF:CD=1:3,∠EMH=∠B,
∴EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,
∵四边形ABCD是矩形,AB=3,BC=6,
∴CD=AB=3,AD=BC=6,∠B=90°,
∴AE=1,EG=2,CF=1,HF=2,BM=1,
∴EM=3-1-1=1,EG=FH,
∴EG FH,
∴四边形EHFG为平行四边形,
∴S四边形EHFG=2×1=2,
故答案为:C。
【分析】如图,延长FH交AB于点M,根据线段之间的关系可以得出AE:AB=AG:AC,CF:CD=CH:CA,根据平行线分线段成比例定理的逆用得出EG//BC,FH//AD,根据平行于三角形一边的直线,截其它两边,所截的三角形与原三角形相似得出△AEG∽△ABC,△CFH∽△CDA,根据相似三角形对应边成比例得出EG:BC=AE:AB=1:3,HF:AD=CF:CD=1:3,根据矩形的性质进而即可得出EG=2,HF=2,根据一组对边平行且相等的四边形是平行四边形判断出四边形EHFG为平行四边形,进而根据平行四边形面积的计算方法即可算出答案。www.21-cn-jy.com
3. C
分析:∵ ,
∴ ,即 ,
∴ ,
∴ .
故答案为:C .
【分析】根据平行线分线段成比例定理,可得, 代入数据求出AE的长,由AC=AE+EC求出AC的长即可.2-1-c-n-j-y
4. A
分析:解:∵AB∥CD∥EF,
∴ = ,
∴A符合题意,
故答案为:A.
【分析】根据平行线分线段成比例定理可得:。
5. A
分析:解:设弟弟的身高是xm
则
解得:x=1.44
故答案为:A.
【分析】设弟弟的身高是xm,根据同一时刻,同一地点,同一平面不同物体的高度与影长成比例列出方程,求解即可。【出处:21教育名师】
6. B
分析:解:由题意得 ,则DE= ,
故答案为:B.
【分析】根据平行线分线段成比例定理得出, 根据比例式即可求出答案。
二、填空题
7. 40380
分析:∵D1E1∥AB? ?D1F1∥AC
∴ ??
∵AB=5?? AC=4
∴ ??? ??
∴
∴4D1E+5D1F=20?
有2019组,即2019×20=40380
故答案为: 40380 。 【分析】根据平行线分线段成比例定理得出 ?? 然后根据等式的性质,将两个等式相加即可得出4D1E+5D1F=20 ,进而利用乘法分配律及加法结合律可知整个代数式共有2019组20,从而根据有理数的乘法法则即可算出答案。
8. 4
分析:解:∵ ,
∴ ,
又 , , ,
∴ 。
故答案为:4。
【分析】根据平行线分线段成比例定理得出 ,由比例式即可建立方程,求解即可得出EF的长。
9.
分析:解:∵L1∥L2∥L3 ,
,
故答案为: .
【分析】根据平行线分线段成比例定理解答即可.
10.
分析:解:如图,设AH=x,GB=y,
∵EH∥BC,
,
∵FG∥AC,
,
由①②可得x= ,y=2,
∴AC= ,BC=7,
∴S△ABC= ,
故答案为 .
【分析】设AH=x,GB=y,再利用平行线分线段成比例定理,由EH∥BC,FG∥AC,可得出对应线段成比例,建立关于x,y的方程组,解方程组求出x,y的值,从而可求出AC,BC的值,然后利用直角三角形的面积公式就可求出△ABC的面积。21·cn·jy·com
11. 168;20
分析:解:连接KI,连接JL,并延长交AB、CD于点M、N,连接FG ∵矩形ABCD ∴AB∥CD ∵ E、F、G、H分别是边AB,CD的三等分点 ∴AE=AB,CG=CD, ∴AE=CG,AE∥CG ∴△AECG是平行四边形 ∴AG∥CE 同理可证:DF∥BH ∴四边形IJKL是平行四边形 ∵AF=DG,AF∥DG,∠FAD=90° ∴四边形AFGD是矩形, ∴IA=ID=IG=IF ∵AI∥EJ ∴即IJ=FI 同理可证IL=GI ∴JL是△IFG的中位线 ∴JL=FG=BC ∴IJ=IL ∴四边形IJKL是菱形, ∴JL⊥IK, ∵IK=AE=AB ∴S菱形IJKL=IK·JL=×AB·BC=AB·BC=×2016=168; ∵AB·BC=2016,AD:AB=8:9 设AD=8x,AB=9x ∴72x2=2016 解之:x= ∴IK=AB=, JL=BC= ∴IO=JL=, LO=IK= 在Rt△ILO中,IL= ∴菱形IJKL的周长为:4×= 故答案为:168; 【分析】连接KI,连接JL,并延长交AB、CD于点M、N,连接FG,利用矩形的性质及已知E、F、G、H分别是边AB,CD的三等分点,易证△AECG是平行四边形,再证明四边形IJKL是平行四边形,四边形AFGD是矩形,利用平行线分线段成比例定理及三角形中位线定理,可证得IJ=IL,从而可证得四边形IJKL是菱形,再证明JL=BC,IK=AB,然后利用菱形的面积等于两对角线之积的一半,就可求出阴影部分的面积;由已知AB·BC=2016,AD:AB=8:9,设AD=8x,AB=9x,列方程求出x的值,从而可求出IO、LO的长,再利用勾股定理求出IL的长,然后利用菱形的性质,就可求出阴影部分的周长。
三、解答题
12. 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,??
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
【解析】【分析】根据光的反射定律作出相关光路图,因为GF∥AC,利用三角形相似分别列比例式。因为根据平面镜成像特点,像和物是等大的,找出有关相等的线段,进行一系列相关的等量代换,使关系式用用已知线段表示,代入已知数据,得出楼的高度。21·世纪*教育网
四、综合题
13. (1)解:如图所示;
(2)解:∵ ,
∴ .
∴ .
【解析】【分析】(1)利用尺规,依次找到角的对应点,画出角即可。 (2)根据两线平行、两角相等,可得到对应的边成比例,得到比值。21教育网
14. (1)证明:①∵四边形ABCD是正方形,
∴AB=BC=4,∠ABC=∠BCD=90°,
在△ABE和△BCF中, ,
∴△ABE≌△BCF(SAS),
∴AE=BF;
②由①得:△ABE≌△BCF,
∴∠BAE=∠CBF,
∵∠CBF+∠ABF=90°,
∴∠BAE+∠ABF=90°,
∴∠AGB=90°,
∴AE⊥BF
(2)解:①如图2所示:
∵E为BC的中点,
∴CF=BE= BC=2,
∴BF ,
由(1)得:AE⊥BF,
∴∠BGE=∠ABE=90°,
∵∠BEG=∠AEB,
∴△BEG∽△AEB,
∴ ,
设GE=x,则BG=2x,
在Rt△BEG中,由勾股定理得:x2+(2x)2=22 ,
解得:x= ,
∴BG=2× ,
∵AB∥CD,
∴ ,即 ,
解得:BH= ;
②由(1)得:∠AGB=90°,
∴点G在以AB为直径的圆上,
设AB的中点为M,
由图形可知:当C、G、M在同一直线上时,CG为最小值,如图3所示:
∵AE⊥BF,
∴∠AGB=90°,
∴GM= AB=BM=2,
∵AB∥CD,
∴ =1,
∴CF=CG,
∵CF=BE,
∴CF=CG=BE,
设CF=CG=BE=a,则CM=a+2,
在Rt△BCM中,由勾股定理得:22+42=(a+2)2 ,
解得:a=2 ﹣2,即
当CG取得最小值时,BE的长为2 ﹣2.
【解析】【分析】(1)①由正方形的性质得出AB=BC,∠ABC=∠BCD=90°,结合已知用边角边可证△ABE≌△BCF,由全等三角形的性质即可求解; ②由①中放入全等三角形可得∠BAE=∠CBF,结合∠CBF+∠ABF=90°可证∠AGB=90°,由垂线的定义即可求解; (2)①由直角三角形的性质得CF=BE=BC,用勾股定理求得BF得值,由(1)的结论得:AE⊥BF,则∠BGE=∠ABE=90°,根据两个角对应相等的两个三角形相似可证△BEG∽△AEB,由相似三角形的性质可得比例式, 设GE=x,则BG=2x,在Rt△BEG中,由勾股定理得关于x的方程,解方程求得BG的值,由平行线分线段成比例定理得比例式, 将已知的线段代入比例式计算即可求得BH的长; ②由(1)的结论得:∠AGB=90°,根据点与圆的位置关系知:点G在以AB为直径的圆上,设AB的中点为M,当C、G、M在同一直线上时,CG为最小值,则GM=AB=BM,由平行线分线段成比例定理得比例式, 结合已知可得CF=CG=BE,设CF=CG=BE=a,则CM=a+2,在Rt△BCM中,由勾股定理得关于a的方程,解方程即可求解.21世纪教育网版权所有
