北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第6讲 二次函数y=a(x-h)^2+ k(a≠0)的图像与性质(基础)含答案
文档属性
| 名称 | 北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第6讲 二次函数y=a(x-h)^2+ k(a≠0)的图像与性质(基础)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 209.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-18 22:02:46 | ||
图片预览



文档简介
二次函数y=a(x-h)2+k(a≠0)的图象与性质—知识讲解(基础)
【学习目标】
1.会用描点法画出二次函数(a、h、k常数,a≠0)的图象.掌握抛物线与图象之间的关系;
2.熟练掌握函数的有关性质,并能用函数的性质解决一些实际问题;
3.经历探索的图象及性质的过程,体验与、、之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴沿轴平移:向上(下)平移个单位,变成
(或)
⑵沿x轴平移:向左(右)平移个单位,变成(或)
【典型例题】
类型一、二次函数图象及性质
1.将抛物线作下列移动,求得到的新抛物线的解析式.
(1)向左平移2个单位,再向下平移3个单位;
(2)顶点不动,将原抛物线开口方向反向;
(3)以x轴为对称轴,将原抛物线开口方向反向.
【答案与解析】
抛物线的顶点为(1,3).
(1)将抛物线向左平移2个单位,再向下平移3个单位后,顶点为(-1,0),而开口方向和形状不变,所以a=2,得到抛物线解析式为.
(2)顶点不动为(1,3),开口方向反向,则,
所得抛物线解析式为.
(3)因为新顶点与原顶点(1,3)关于x轴对称,故新顶点应为(1,-3).又∵ 抛物线开口反向,
∴ .故所得抛物线解析式为.
【总结升华】当抛物线的形状确定以后,其位置完全决定于顶点,方向决定于a的符号,故可利用移动后的顶点坐标与开口方向求移动后的抛物线的解析式.
举一反三:
【变式】将抛物线向右平移2个单位,再向上平移5个单位,得到的抛物线解析式为 .
【答案】.
2.(2019?荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
【答案与解析】
解:y=x2﹣6x+5=(x﹣3)2﹣4,
∴抛物线的顶点坐标为(3,﹣4),
把点(3,﹣4)向上平移2个单位长度,再向右平移1个单位长度得到点的坐标为(4,﹣2),
∴平移后得到的抛物线解析式为y=(x﹣4)2﹣2.
【总结升华】由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
举一反三:
【变式】二次函数的图象可以看作是二次函数的图象向 平移4个单位,再向 平移3个单位得到的.
【答案】上;右.
类型二、二次函数性质的综合应用
3.(2019秋?安顺期末)二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
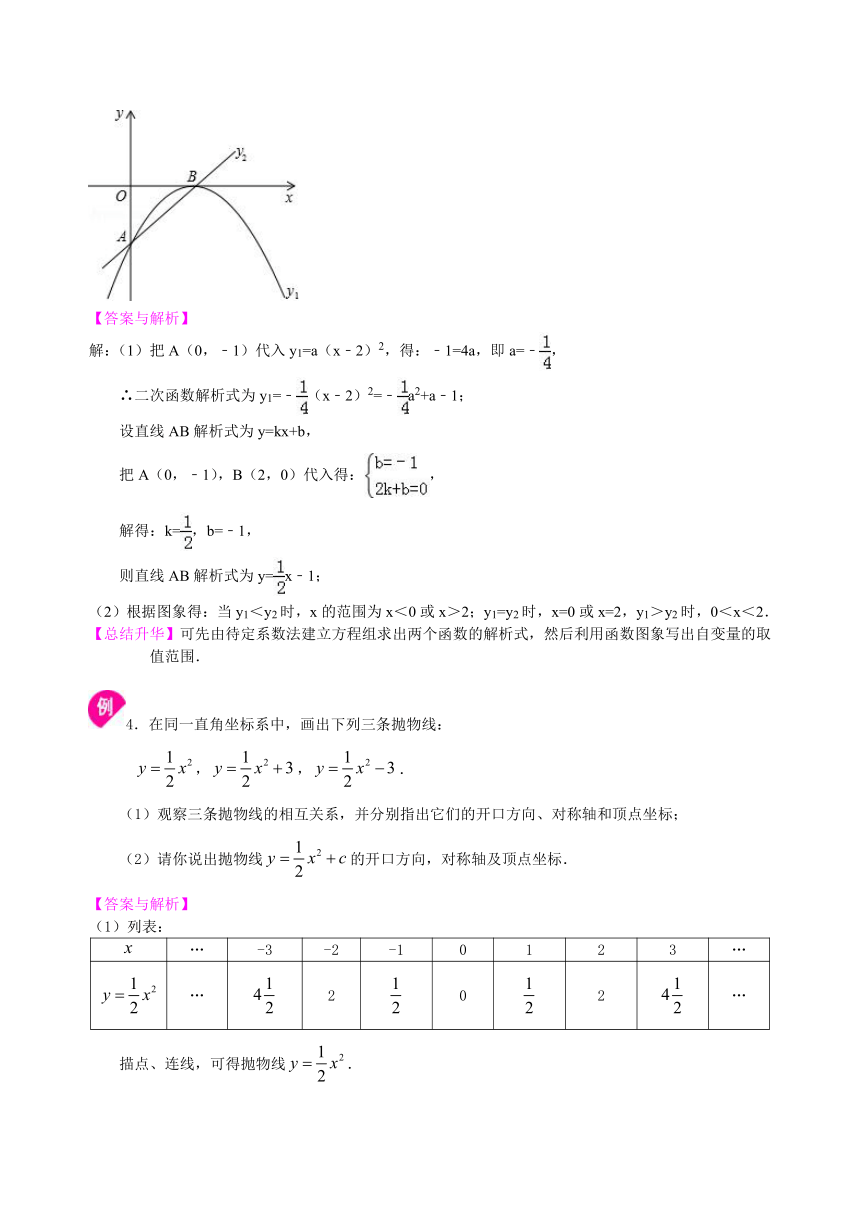
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
【答案与解析】
解:(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a=﹣,
∴二次函数解析式为y1=﹣(x﹣2)2=﹣a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:,
解得:k=,b=﹣1,
则直线AB解析式为y=x﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
【总结升华】可先由待定系数法建立方程组求出两个函数的解析式,然后利用函数图象写出自变量的取值范围.
4.在同一直角坐标系中,画出下列三条抛物线:
,,.
(1)观察三条抛物线的相互关系,并分别指出它们的开口方向、对称轴和顶点坐标;
(2)请你说出抛物线的开口方向,对称轴及顶点坐标.
【答案与解析】
(1)列表:
…
-3
-2
-1
0
1
2
3
…
…
2
0
2
…
描点、连线,可得抛物线.
将的图象分别向上和向下平移3个单位,就分别得到与的图象(如图所示).
抛物线,与开口都向上,对称轴都是y轴,顶点坐标依次
是(0,0)、(0,3)和(0,-3).
(2)抛物线的开口向上,对称轴是y轴(或直线),顶点坐标为(0,c).
【总结升华】先用描点法画出的图象,再用平移法得到另两条抛物线,并根据图象回答问题.
规律总结:.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(基础)
【巩固练习】
一、选择题 1.抛物线的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.函数y=x2+2x+1写成y=a(x-h)2+k的形式是( )
A.y=(x-1)2+2 B.y=(x-1)2+ C.y=(x-1)2-3 D.y=(x+2)2-1
3.抛物线y=x2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( )
A.y=(x+3)2-2 B.y=(x-3)2+2 C.y=(x-3)2-2 D.y=(x+3)2+2
4.把二次函数配方成顶点式为( )
A. B. C. D.
5.由二次函数,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线
C.其最小值为1 D.当时,y随x的增大而增大
6.(2019?泰安)在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( ).
A. B. C. D.
二、填空题
7. (2019?怀化)二次函数y=x2+2x的顶点坐标为 ,对称轴是直线 .
8.已知抛物线y=-2(x+1)2-3,如果y随x的增大而减小,那么x的取值范围是_ _____.
9.抛物线y=-3(2x2-1)的开口方向是_____,对称轴是_____.
10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
11.将抛物线向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.
12.抛物线的顶点为C,已知的图象经过点C,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.
三、解答题
13.已知抛物线的顶点(-1,-2),且图象经过(1,10),求抛物线的解析式.
14. 已知抛物线向上平移2个单位长度,再向右平移1个单位长度得到
抛物线;
(1)求出a,h,k的值;
(2)在同一直角坐标系中,画出与的图象;
(3)观察的图象,当________时,y随x的增大而增大;
当________时,函数y有最________值,最________值是________;
(4)观察的图象,你能说出对于一切的值,函数y的取值范围吗?
15.(2019?珠海)已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
【答案与解析】
一、选择题 1.【答案】D;
【解析】由顶点式可求顶点,由得,此时,.
2.【答案】D;
【解析】通过配方即可得到结论.
3.【答案】A;
【解析】抛物线 y=x2向左平移3个单位得到y=(x+3)2,再向下平移2个单位后,
所得的抛物线表达式是y=(x+3)2-2.
4.【答案】B;
【解析】通过配方即可得到结论.
5.【答案】C;
【解析】可画草图进行判断.
6.【答案】D;
【解析】解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;
B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;
C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;
D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,
故选D.
二、填空题
7.【答案】(﹣1,﹣1); x=﹣1;
【解析】∵y=x2+2x=(x+1)2﹣1,
∴二次函数y=x2+4x的顶点坐标是:(﹣1,﹣1),对称轴是直线x=﹣1.
8.【答案】x≥-1;
【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y随x的增大而减小,
故x≥-1.
9.【答案】向下,y轴;
10.【答案】;
【解析】设过点(1,-14)得,所以.
11.【答案】;
【解析】先化一般式为顶点式,再根据平移规律求解.
12.【答案】 1;
【解析】C(2,-6),可求与x轴交于,与y轴交于(0,3),∴ .
三、解答题
13.【答案与解析】
∵ 抛物线的顶点为(-1,-2),
∴ 设其解析式为,
又图象经过点(1,10),∴ ,∴ ,
∴ 解析式为.
14.【答案与解析】
(1)由向上平移2个单位,再向右平移1个单位所得到的抛物线是.
∴ ,,.
(2)函数与的图象如图所示.
(3)观察的图象,当时,随x的增大而增大;
当时,函数有最大值,最大值是.
(4)由图象知,对于一切的值,总有函数值.
15.【答案与解析】
(1)证明:∵对称轴是直线x=1=﹣,
∴2a+b=0;
(2)解:∵ax2+bx﹣8=0的一个根为4,
∴16a+4b﹣8=0,
∵2a+b=0,
∴b=﹣2a,
∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,
∴ax2+bx﹣8=0为:x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
解得:x1=4,x2=﹣2,
故方程的另一个根为:﹣2.
【学习目标】
1.会用描点法画出二次函数(a、h、k常数,a≠0)的图象.掌握抛物线与图象之间的关系;
2.熟练掌握函数的有关性质,并能用函数的性质解决一些实际问题;
3.经历探索的图象及性质的过程,体验与、、之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴沿轴平移:向上(下)平移个单位,变成
(或)
⑵沿x轴平移:向左(右)平移个单位,变成(或)
【典型例题】
类型一、二次函数图象及性质
1.将抛物线作下列移动,求得到的新抛物线的解析式.
(1)向左平移2个单位,再向下平移3个单位;
(2)顶点不动,将原抛物线开口方向反向;
(3)以x轴为对称轴,将原抛物线开口方向反向.
【答案与解析】
抛物线的顶点为(1,3).
(1)将抛物线向左平移2个单位,再向下平移3个单位后,顶点为(-1,0),而开口方向和形状不变,所以a=2,得到抛物线解析式为.
(2)顶点不动为(1,3),开口方向反向,则,
所得抛物线解析式为.
(3)因为新顶点与原顶点(1,3)关于x轴对称,故新顶点应为(1,-3).又∵ 抛物线开口反向,
∴ .故所得抛物线解析式为.
【总结升华】当抛物线的形状确定以后,其位置完全决定于顶点,方向决定于a的符号,故可利用移动后的顶点坐标与开口方向求移动后的抛物线的解析式.
举一反三:
【变式】将抛物线向右平移2个单位,再向上平移5个单位,得到的抛物线解析式为 .
【答案】.
2.(2019?荆州)将抛物线y=x2﹣6x+5向上平移2个单位长度,再向右平移1个单位长度后,求得到的抛物线解析式.
【答案与解析】
解:y=x2﹣6x+5=(x﹣3)2﹣4,
∴抛物线的顶点坐标为(3,﹣4),
把点(3,﹣4)向上平移2个单位长度,再向右平移1个单位长度得到点的坐标为(4,﹣2),
∴平移后得到的抛物线解析式为y=(x﹣4)2﹣2.
【总结升华】由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.
举一反三:
【变式】二次函数的图象可以看作是二次函数的图象向 平移4个单位,再向 平移3个单位得到的.
【答案】上;右.
类型二、二次函数性质的综合应用
3.(2019秋?安顺期末)二次函数y1=a(x﹣2)2的图象与直线y2交于A(0,﹣1),B(2,0)两点.
(1)确定二次函数与直线AB的解析式.
(2)如图,分别确定当y1<y2,y1=y2,y1>y2时,自变量x的取值范围.
【答案与解析】
解:(1)把A(0,﹣1)代入y1=a(x﹣2)2,得:﹣1=4a,即a=﹣,
∴二次函数解析式为y1=﹣(x﹣2)2=﹣a2+a﹣1;
设直线AB解析式为y=kx+b,
把A(0,﹣1),B(2,0)代入得:,
解得:k=,b=﹣1,
则直线AB解析式为y=x﹣1;
(2)根据图象得:当y1<y2时,x的范围为x<0或x>2;y1=y2时,x=0或x=2,y1>y2时,0<x<2.
【总结升华】可先由待定系数法建立方程组求出两个函数的解析式,然后利用函数图象写出自变量的取值范围.
4.在同一直角坐标系中,画出下列三条抛物线:
,,.
(1)观察三条抛物线的相互关系,并分别指出它们的开口方向、对称轴和顶点坐标;
(2)请你说出抛物线的开口方向,对称轴及顶点坐标.
【答案与解析】
(1)列表:
…
-3
-2
-1
0
1
2
3
…
…
2
0
2
…
描点、连线,可得抛物线.
将的图象分别向上和向下平移3个单位,就分别得到与的图象(如图所示).
抛物线,与开口都向上,对称轴都是y轴,顶点坐标依次
是(0,0)、(0,3)和(0,-3).
(2)抛物线的开口向上,对称轴是y轴(或直线),顶点坐标为(0,c).
【总结升华】先用描点法画出的图象,再用平移法得到另两条抛物线,并根据图象回答问题.
规律总结:.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(基础)
【巩固练习】
一、选择题 1.抛物线的顶点坐标是( )
A.(2,-3) B.(-2,3) C.(2,3) D.(-2,-3)
2.函数y=x2+2x+1写成y=a(x-h)2+k的形式是( )
A.y=(x-1)2+2 B.y=(x-1)2+ C.y=(x-1)2-3 D.y=(x+2)2-1
3.抛物线y=x2向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( )
A.y=(x+3)2-2 B.y=(x-3)2+2 C.y=(x-3)2-2 D.y=(x+3)2+2
4.把二次函数配方成顶点式为( )
A. B. C. D.
5.由二次函数,可知( )
A.其图象的开口向下 B.其图象的对称轴为直线
C.其最小值为1 D.当时,y随x的增大而增大
6.(2019?泰安)在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( ).
A. B. C. D.
二、填空题
7. (2019?怀化)二次函数y=x2+2x的顶点坐标为 ,对称轴是直线 .
8.已知抛物线y=-2(x+1)2-3,如果y随x的增大而减小,那么x的取值范围是_ _____.
9.抛物线y=-3(2x2-1)的开口方向是_____,对称轴是_____.
10.顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为 .
11.将抛物线向上平移3个单位,再向右平移4个单位得到的抛物线是__ _____.
12.抛物线的顶点为C,已知的图象经过点C,则这个一次函数的图象与两坐标轴所围成的三角形面积为________.
三、解答题
13.已知抛物线的顶点(-1,-2),且图象经过(1,10),求抛物线的解析式.
14. 已知抛物线向上平移2个单位长度,再向右平移1个单位长度得到
抛物线;
(1)求出a,h,k的值;
(2)在同一直角坐标系中,画出与的图象;
(3)观察的图象,当________时,y随x的增大而增大;
当________时,函数y有最________值,最________值是________;
(4)观察的图象,你能说出对于一切的值,函数y的取值范围吗?
15.(2019?珠海)已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
【答案与解析】
一、选择题 1.【答案】D;
【解析】由顶点式可求顶点,由得,此时,.
2.【答案】D;
【解析】通过配方即可得到结论.
3.【答案】A;
【解析】抛物线 y=x2向左平移3个单位得到y=(x+3)2,再向下平移2个单位后,
所得的抛物线表达式是y=(x+3)2-2.
4.【答案】B;
【解析】通过配方即可得到结论.
5.【答案】C;
【解析】可画草图进行判断.
6.【答案】D;
【解析】解:A、由直线与y轴的交点在y轴的负半轴上可知,n2<0,错误;
B、由抛物线与y轴的交点在y轴的正半轴上可知,m>0,由直线可知,﹣m>0,错误;
C、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m<0,错误;
D、由抛物线y轴的交点在y轴的负半轴上可知,m<0,由直线可知,﹣m>0,正确,
故选D.
二、填空题
7.【答案】(﹣1,﹣1); x=﹣1;
【解析】∵y=x2+2x=(x+1)2﹣1,
∴二次函数y=x2+4x的顶点坐标是:(﹣1,﹣1),对称轴是直线x=﹣1.
8.【答案】x≥-1;
【解析】由解析式可得抛物线的开口向下,对称轴是x=-1,对称轴的右边是y随x的增大而减小,
故x≥-1.
9.【答案】向下,y轴;
10.【答案】;
【解析】设过点(1,-14)得,所以.
11.【答案】;
【解析】先化一般式为顶点式,再根据平移规律求解.
12.【答案】 1;
【解析】C(2,-6),可求与x轴交于,与y轴交于(0,3),∴ .
三、解答题
13.【答案与解析】
∵ 抛物线的顶点为(-1,-2),
∴ 设其解析式为,
又图象经过点(1,10),∴ ,∴ ,
∴ 解析式为.
14.【答案与解析】
(1)由向上平移2个单位,再向右平移1个单位所得到的抛物线是.
∴ ,,.
(2)函数与的图象如图所示.
(3)观察的图象,当时,随x的增大而增大;
当时,函数有最大值,最大值是.
(4)由图象知,对于一切的值,总有函数值.
15.【答案与解析】
(1)证明:∵对称轴是直线x=1=﹣,
∴2a+b=0;
(2)解:∵ax2+bx﹣8=0的一个根为4,
∴16a+4b﹣8=0,
∵2a+b=0,
∴b=﹣2a,
∴16a﹣8a﹣8=0,
解得:a=1,则b=﹣2,
∴ax2+bx﹣8=0为:x2﹣2x﹣8=0,
则(x﹣4)(x+2)=0,
解得:x1=4,x2=﹣2,
故方程的另一个根为:﹣2.
