第三章 位置与坐标单元检测题A卷(含解析)
文档属性
| 名称 | 第三章 位置与坐标单元检测题A卷(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 299.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-19 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第三章《位置与坐标》检测题A卷
评卷人 得 分
一.选择题(共12小题)
1.在平面直角坐标系中,点A(2,﹣3)位于哪个象限?( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
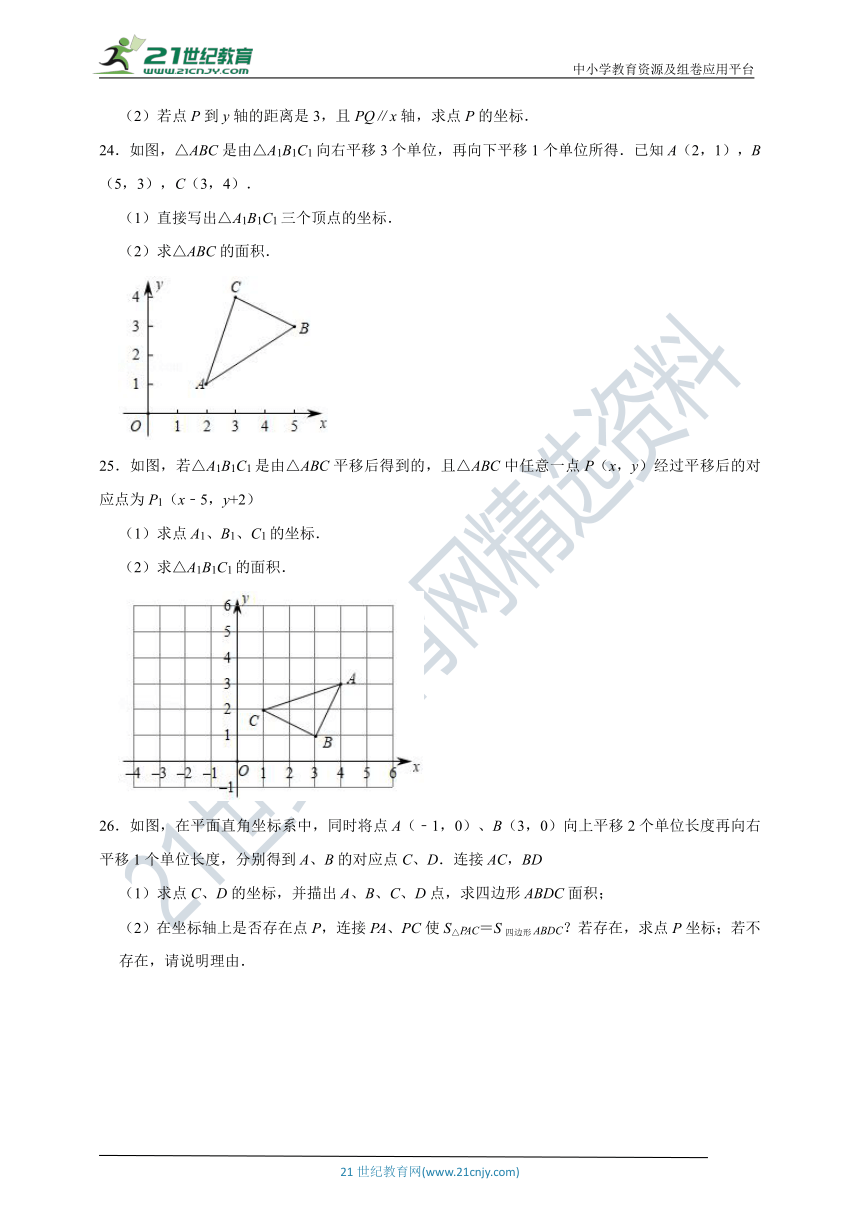
2.如图的坐标平面上有原点O与A、B、C、D四点.若有一直线L通过点(﹣3,4)且与y轴垂直,则L也会通过下列哪一点?( )
A.A B.B C.C D.D
3.若点A(a+1,b﹣2)在第二象限,则点B(﹣a,1﹣b)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.在平面直角坐标系的第二象限内有一点M,点M到x轴的距离为3,到y轴的距离为4,则点M的坐标是( )
A.(3,﹣4) B.(4,﹣3) C.(﹣4,3) D.(﹣3,4)
5.如图,在平面直角坐标系中,将△ABO沿x轴向右滚动到△AB1C1的位置,再到△A1B1C2的位置……依次进行下去,若已知点A(4,0),B(0,3),则点C100的坐标为( )
A.(1200,) B.(600,0) C.(600,) D.(1200,0)
6.在平面直角坐标系中,一个智能机器人接到的指令是:从原点O出发,按“向上→向右→向下→向右”的方向依次不断移动,每次移动1个单位长度,其移动路线如图所示,第一次移动到点A1,第二次移动到点A2……第n次移动到点An,则点A2019的坐标是( )
A.(1010,0) B.(1010,1) C.(1009,0) D.(1009,1)
7.在平面直角坐标系中,点A(m,2)与点B(3,n)关于y轴对称,则( )
A.m=3,n=2 B.m=﹣3,n=2 C.m=2,n=3 D.m=﹣2,n=﹣3
8.若点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,则m+n的值是( )
A.﹣5 B.﹣3 C.3 D.1
9.在平面直角坐标系中,点P(﹣3,m2+1)关于原点对称点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
10.在平面直角坐标系中,将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为( )
A.(3,﹣1) B.(3,3) C.(1,1) D.(5,1)
11.在平面直角坐标系中,将点(2,1)向右平移3个单位长度,则所得的点的坐标是( )
A.(0,5) B.(5,1) C.(2,4) D.(4,2)
12.如图,在平面直角坐标系xOy中,将四边形ABCD先向下平移,再向右平移得到四边形A1B1C1D1,已知A(﹣3,5),B(﹣4,3),A1(3,3),则B1的坐标为( )
A.(1,2) B.(2,1) C.(1,4) D.(4,1)
评卷人 得 分
二.填空题(共6小题)
13.中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“兵”位于点 .
14.已知线段AB∥y轴,且AB=3,若点A的坐标为(1,﹣2).则点B的坐标是
15.点P(2,4)与点Q(﹣3,4)之间的距离是 .
16.若点P(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,那么y的值为 .
17.第四象限有一个点M(x,y),且|x|=4,|y﹣1|=5,则点M关于x轴对称点的坐标是 .
18.△ABC的顶点A(3,﹣1),现将△ABC先向上平移3个单位,在向左平移2个单位后,则点A的坐标是 .
评卷人 得 分
三.解答题(共8小题)
19.在平面直角坐标系中,有A(﹣2,a+1),B(a﹣1,4),C(b﹣2,b)三点.
(1)当AB∥x轴时,求A、B两点间的距离;
(2)当CD⊥x轴于点D,且CD=1时,求点C的坐标.
20.已知,点P(2m﹣6,m+2).
(1)若点P在y轴上,P点的坐标为 ;
(2)若点P的纵坐标比横坐标大6,求点P在第几象限?
(3)若点P和点Q都在过A(2,3)点且与x轴平行的直线上,AQ=3,求Q点的坐标.
21.已知点P(2m+4,m﹣1),请分别根据下列条件,求出点P的坐标.
(1)点P的横坐标比纵坐标大3;
(2)点P在过点A(2,﹣4)且与y轴平行的直线上.
22.已知点M(3a﹣2,a+6).
(1)若点M在x轴上,求点M的坐标
(2)变式一:已知点M(3a﹣2,a+6),点N(2,5),且直线MN∥x轴,求点M的坐标.
(3)变式二:已知点M(3a﹣2,a+6),若点M到x轴、y轴的距离相等,求点M的坐标.
23.已知P(a+1,b﹣2),Q(4,3)两点.
(1)若P,Q两点关于x轴对称,求a+b的值
(2)若点P到y轴的距离是3,且PQ∥x轴,求点P的坐标.
24.如图,△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得.已知A(2,1),B(5,3),C(3,4).
(1)直接写出△A1B1C1三个顶点的坐标.
(2)求△ABC的面积.
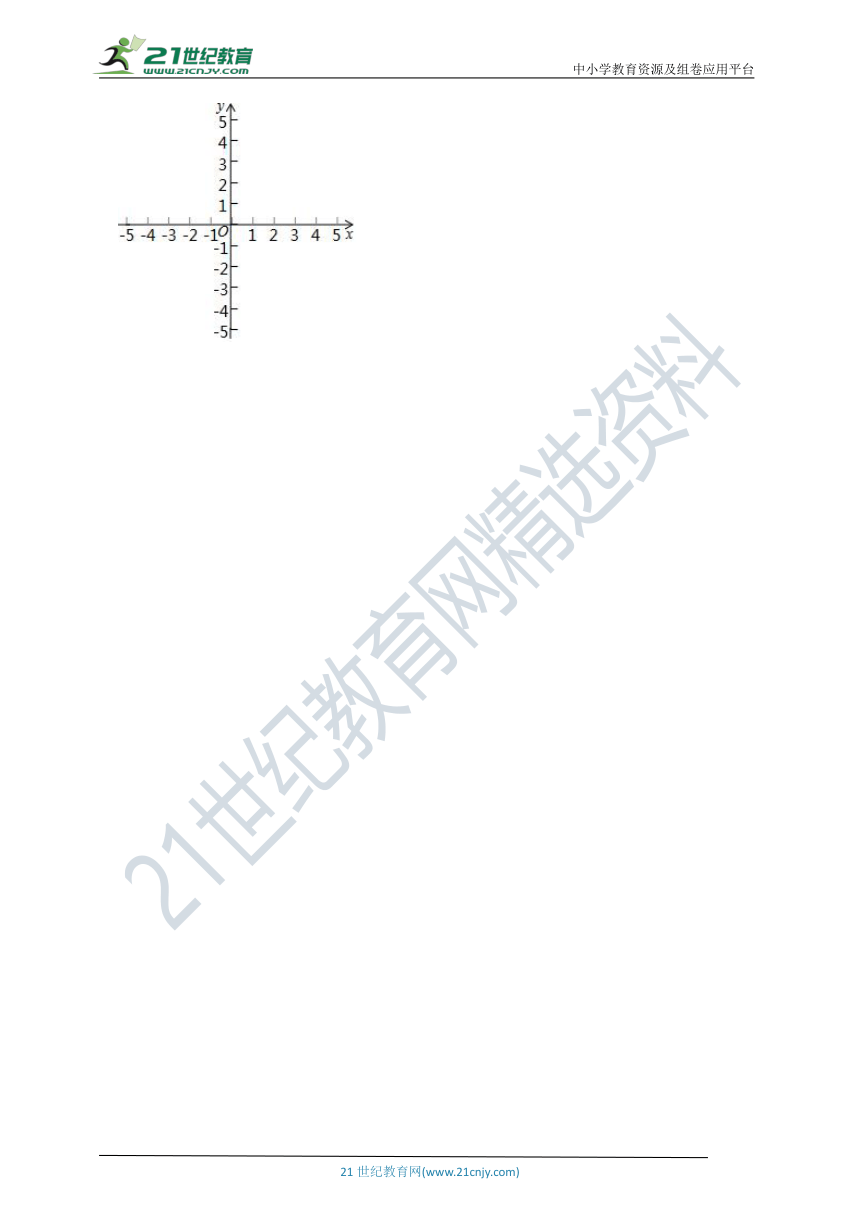
25.如图,若△A1B1C1是由△ABC平移后得到的,且△ABC中任意一点P(x,y)经过平移后的对应点为P1(x﹣5,y+2)
(1)求点A1、B1、C1的坐标.
(2)求△A1B1C1的面积.
26.如图,在平面直角坐标系中,同时将点A(﹣1,0)、B(3,0)向上平移2个单位长度再向右平移1个单位长度,分别得到A、B的对应点C、D.连接AC,BD
(1)求点C、D的坐标,并描出A、B、C、D点,求四边形ABDC面积;
(2)在坐标轴上是否存在点P,连接PA、PC使S△PAC=S四边形ABDC?若存在,求点P坐标;若不存在,请说明理由.
答案与解析
一.选择题(共12小题)
1.分析:根据各象限内点的坐标特征解答即可.
解:点A坐标为(2,﹣3),则它位于第四象限,
故选:D.
2.分析:直接利用点的坐标,正确结合坐标系分析即可.
解:如图所示:有一直线L通过点(﹣3,4)且与y轴垂直,故L也会通过D点.
故选:D.
3.分析:直接利用第二象限横纵坐标的关系得出a,b的符号,进而得出答案.
解:∵点A(a+1,b﹣2)在第二象限,
∴a+1<0,b﹣2>0,
解得:a<﹣1,b>2,
则﹣a>1,1﹣b<﹣1,
故点B(﹣a,1﹣b)在第四象限.
故选:D.
4.分析:根据第二象限内点的坐标特征,可得答案.
解:由题意,得
x=﹣4,y=3,
即M点的坐标是(﹣4,3),
故选:C.
5.分析:根据三角形的滚动,可得出:每滚动3次为一个周期,点C1,C3,C5,…在第一象限,点C2,C4,C6,…在x轴上,由点A,B的坐标利用勾股定理可求出AB的长,进而可得出点C2的横坐标,同理可得出点C4,C6的横坐标,根据点的横坐标的变化可找出变化规律“点C2n的横坐标为2n×6(n为正整数)”,再代入2n=100即可求出结论.
解:根据题意,可知:每滚动3次为一个周期,点C1,C3,C5,…在第一象限,点C2,C4,C6,…在x轴上.
∵A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB==5,
∴点C2的横坐标为4+5+3=12=2×6,
同理,可得出:点C4的横坐标为4×6,点C6的横坐标为6×6,…,
∴点C2n的横坐标为2n×6(n为正整数),
∴点C100的横坐标为100×6=600,
∴点C100的坐标为(600,0).
故选:B.
6.分析:根据图象可得移动4次图象完成一个循环,从而可得出点A2019的坐标.
解:A1(0,1),A2(1,1),A3(1,0),A4(2,0),A5(2,1),A6(3,1),…,
2019÷4=504…3,
所以A2019的坐标为(504×2+1,0),
则A2019的坐标是(1009,0).
故选:C.
7.分析:直接利用关于y轴对称点的性质得出答案.
解:∵点A(m,2)与点B(3,n)关于y轴对称,
∴m=﹣3,n=2.
故选:B.
8.分析:根据关于y轴的对称点的坐标特点:横坐标互为相反数,纵坐标不变,据此求出m、n的值,代入计算可得.
解:∵点A(1+m,1﹣n)与点B(﹣3,2)关于y轴对称,
∴1+m=3、1﹣n=2,
解得:m=2、n=﹣1,
所以m+n=2﹣1=1,
故选:D.
9.分析:依据m2+1>0,即可得出点P(﹣3,m2+1)在第二象限,再根据两个点关于原点对称时,它们的坐标符号相反,即可得出结论.
解:∵m2+1>0,
∴点P(﹣3,m2+1)在第二象限,
∴点P(﹣3,m2+1)关于原点对称点在第四象限,
故选:D.
10.分析:根据向下平移,横坐标不变、纵坐标相减列式计算即可得解.
解:将点P(3,1)向下平移2个单位长度,得到的点P′的坐标为(3,1﹣2),即(3,﹣1),
故选:A.
11.分析:在平面直角坐标系中,将点(2,1)向右平移时,横坐标增加,纵坐标不变.
解:将点(2,1)向右平移3个单位长度,则所得的点的坐标是(5,1).
故选:B.
12.分析:根据A和A1的坐标得出四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,则B的平移方法与A点相同,即可得到答案.
解:由A(﹣3,5),A1(3,3)可知四边形ABCD先向下平移2个单位,再向右平移6个单位得到四边形A1B1C1D1,
∵B(﹣4,3),
∴B1的坐标为(2,1),
故选:B.
二.填空题(共6小题)
13.分析:直接利用“帅”位于点(0,﹣2),可得原点的位置,进而得出“兵”的坐标.
解:如图所示:可得原点位置,则“兵”位于(﹣1,1).
故答案为:(﹣1,1).
14.分析:根据平行于y轴的点的横坐标相同可得点B的横坐标,再分点B在点A的上方与下方两种情况讨论求解.
解:∵AB∥y轴,点A的坐标为(1,﹣2),
∴点B的横坐标为1,
∵AB=3,
∴点B在点A的上方时,点B的纵坐标为1,点B的坐标为(1,1),
点B在点A的下方时,点B的纵坐标为﹣5,点B的坐标为(1,﹣5),
综上所述,点B的坐标为(1,1)或(1,﹣5).
故答案为:(1,1)或(1,﹣5).
15.分析:根据x轴上或平行于x轴的直线上两点的距离为两点横坐标的差的绝对值解答即可.
解:∵点P(2,4),点Q(﹣3,4)
∴PQ∥x轴,
∵x轴上或平行于x轴的直线上两点的距离为 两点横坐标的差的绝对值,
∴PQ=|﹣3﹣2|=5,
故答案为5.
16.分析:直接利用关于y轴对称点的性质得出答案.
解:∵点P(x,4﹣y)与点B(1﹣y,2x)关于y轴对称,
∴,
解得:,
故y=2.
故答案为:2.
17.分析:直接利用第四象限内点的坐标特点得出x,y的值,进而利用关于x轴对称点的性质得出答案.
解:∵第四象限有一个点M(x,y),且|x|=4,|y﹣1|=5,
∴x=4,y﹣1=﹣5,
解得:y=﹣4,
故点M的坐标为:(4,﹣4),
则点M关于x轴对称点的坐标是:(4,4).
故答案为:(4,4).
18.分析:把点A的横坐标减去2,纵坐标加上3即可.
解:由题意,可得平移后点A的横坐标是3﹣2=1,纵坐标是﹣1+3=2,即(1,2).
故答案为(1,2).
三.解答题(共8小题)
19.分析:(1)根据平行于x轴的一条直线上点的纵坐标相等求得a值,进一步求得A、B两点间的距离即可;
(2)根据垂直于x轴的一条直线上点的横坐标相等得到D(b﹣2,0),再根据CD=1,可得|b|=1,求得b值,从而得到点C的坐标.
解:(1)∵AB∥x轴,∴A、B两点的纵坐标相同.
∴a+1=4,
解得a=3.
∴A、B两点间的距离是|(a﹣1)+2|=|3﹣1+2|=4.
(2)∵CD⊥x轴,
∴C、D两点的横坐标相同.
∴D(b﹣2,0).
∵CD=1,
∴|b|=1,
解得b=±1.
当b=1时,点C的坐标是(﹣1,1).
当b=﹣1时,点C的坐标是(﹣3,﹣1).
20.分析:(1)y轴上点的坐标特点是横坐标为0,据此求解可得;
(2)由题意可列出等式2m﹣6+6=m+2,求解即可;
(3)与x轴平行的直线上点的特点是纵坐标都相等,根据这个性质即可求解.
解:(1)∵点P在y轴上,
∴2m﹣6=0,解得m=3,
∴P点的坐标为(0,5);
故答案为(0,5);
(2)根据题意得2m﹣6+6=m+2,解得m=2,
∴P点的坐标为(﹣2,4),
∴点P在第二象限;
(3)∵点P和点Q都在过A(2,3)点且与x轴平行的直线上,
∴点P和点Q的纵坐标都为3,
而AQ=3,
∴Q点的横坐标为﹣1或5,
∴Q点的坐标为(﹣1,3)或(5,3).
21.分析:(1)根据横坐标比纵坐标大3列方程求出m的值,再求解即可;
(2)根据平行于y轴的直线上的点的横坐标相等列方程求出m的值,再求解即可.
解:(1)∵点P(2m+4,m﹣1)的横坐标比纵坐标大3,
∴(2m+4)﹣(m﹣1)=3,解得m=﹣2,
∴2m+4=2×(﹣2)+4=0,m﹣1=﹣2﹣1=﹣3,
∴点P的坐标为(0,﹣3);
(2)∵点P(2m+4,m﹣1)在过点A(2,﹣4)且与y轴平行的直线上,
∴2m+4=2,解得m=﹣1,
∴m﹣1=﹣1﹣1=﹣2,
∴点P的坐标为(2,﹣2).
22.分析:(1)根据x轴上点的纵坐标为0列式计算即可得解;
(2)根据平行于x轴的点的纵坐标相同列出方程求出a的值,然后即可得解.
(3)根据象限平分线上点到x轴、y轴的距离相等列式计算即可得解.
解:(1)∵点M在x轴上,
∴a+6=0,
∴a=﹣6,
3a﹣2=﹣18﹣2=﹣20,a+6=0,
∴点M的坐标是(﹣20,0);
(2)∵直线MN∥x轴,
∴a+6=5,
解得a=﹣1,
3a﹣2=3×(﹣1)﹣2=﹣5,
所以,点M的坐标为(﹣5,5).
(3)∵点M到x轴、y轴的距离相等,
∴3a﹣2=a+6,或3a﹣2+a+6=0
解得:a=4,或a=﹣1,
所以点M的坐标为(10,10)或(﹣5,5).
23.分析:(1)依据P,Q两点关于x轴对称,即可得到a,b的值,进而得出a+b的值;
(2)依据点P到y轴的距离是3,且PQ∥x轴,即可得到点P的坐标.
解:(1)∵P,Q两点关于x轴对称,
∴a+1=4,b﹣2=﹣3,
∴a=3,b=﹣1,
∴a+b=3﹣1=2;
(2)∵点P到y轴的距离是3,
∴点P的横坐标为3或﹣3,
又∵PQ∥x轴,
∴点P的纵坐标为3,
∴P(3,3)或(﹣3,3).
24.分析:(1)根据平移规律即可得到结论,
(2)根据三角形的面积公式即可得到结论.
解:(1)因为△ABC是由△A1B1C1向右平移3个单位,再向下平移1个单位所得
所以,△A1B1C1是由△ABC向左平移3个单位,再向上平移1个单位所得A1(﹣1,2),B1(2,4),C1 (0,5);
(2)如图,△ABC的面积=3×3﹣×1×3﹣×1×2﹣×2×3=3.5.
25.分析:(1)由△ABC中任意一点P(x,y)经平移后对应点为P1(x﹣5,y+2)可得△ABC的平移规律为:向左平移5个单位,向上平移2个单位,由此得到点A、B、C的对应点A1、B1、C1的坐标.
(2)利用矩形的面积减去三个顶点上三角形的面积即可.
解:(1)∵△ABC中任意一点P(x,y)经平移后对应点为P1(x﹣5,y+2),
∴△ABC的平移规律为:向左平移5个单位,向上平移2个单位,
∵A(4,3),B(3,1),C(1,2),
∴点A1的坐标为(﹣1,5),点B1的坐标为(﹣2,3),点C1的坐标为(﹣4,4).
(2)如图所示,
△A1B1C1的面积=3×2﹣×1×3﹣×1×2﹣×1×2=.
26.分析:(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可,再根据平行四边形的面积公式列式计算即可得解;
(2)分点P在x轴和y轴上两种情况,依据S△PAC=S四边形ABDC求解可得.
解:(1)由题意知点C坐标为(﹣1+1,0+2),即(0,2),
点D的坐标为(3+1,0+2),即(4,2),
如图所示,
S四边形ABDC=2×4=8;
(2)当P在x轴上时,
∵S△PAC=S四边形ABDC,
∴,
∵OC=2,
∴AP=8,
∴点P的坐标为 (7,0)或 (﹣9,0);
当P在y轴上时,
∵S△PAC=S四边形ABDC,
∴,
∵OA=1,
∴CP=16,
∴点P的坐标为(0,18)或 (0,﹣14);
综上,点P的坐标为(7,0)或 (﹣9,0)或(0,18)或 (0,﹣14).
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2019/10/15 21:45:32;用户:ct7508;邮箱:ct7508@163.com;学号:20677464
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
