人教版七年级数学上册第3章一元一次方程3.4实际问题与一元一次方程课件(4课时共46张)
文档属性
| 名称 | 人教版七年级数学上册第3章一元一次方程3.4实际问题与一元一次方程课件(4课时共46张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-19 00:00:00 | ||
图片预览









文档简介
(共46张PPT)
3.4.1 实际问题与一元一次方程
一、提出问题。
前面我们学习了一元一次方程的解法,本节课,我们讨论一元一次方程的应用。生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
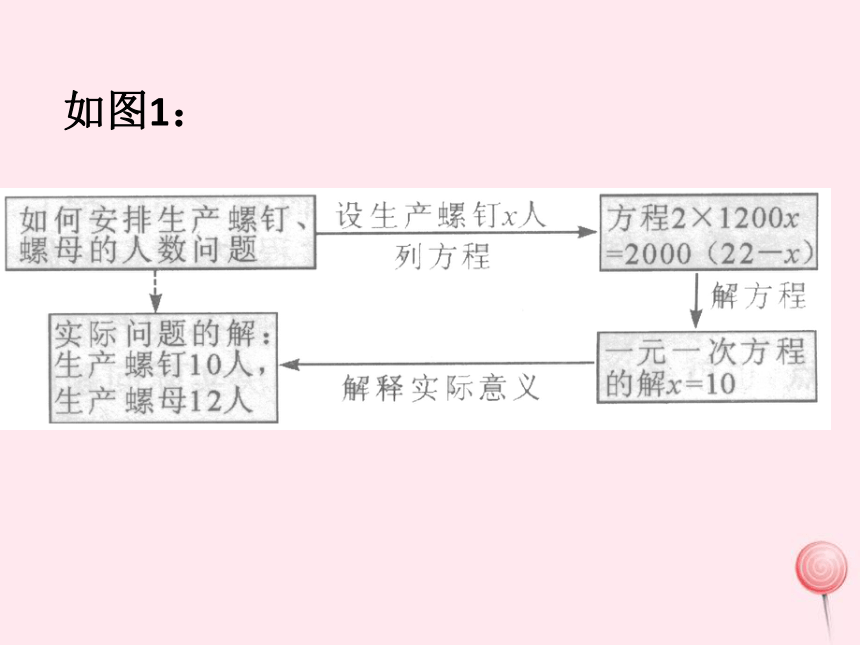
例1.(教科书中例1)某车问有2 2名工人,每人每天可以生产1200个螺钉或2 000个螺母。 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少人?
二、解决问题,初步体会。
如图1:
三、变式训练
某车间有22名工人,每人每天可以生产1200个A部件或3000个B部件,一套机器由1个A部件和3个B部件构成,为使每天生产的A部件和B部件配套,应分别安排生产A、B部件各多少人?
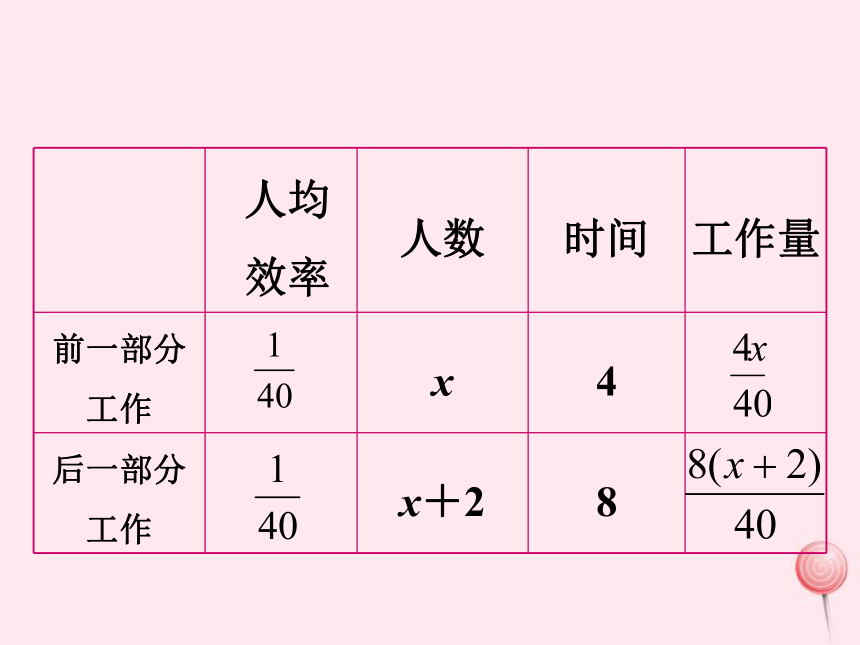
例2. 一批螺钉和螺母需要打包,由一个人做40
小时才能完成。现计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人参与这项工作?
四、解决问题,再次体会。
人均
效率 人数 时间 工作量
前一部分
工作 x 4
后一部分
工作 x+2 8
五、归纳总结,提炼思想。
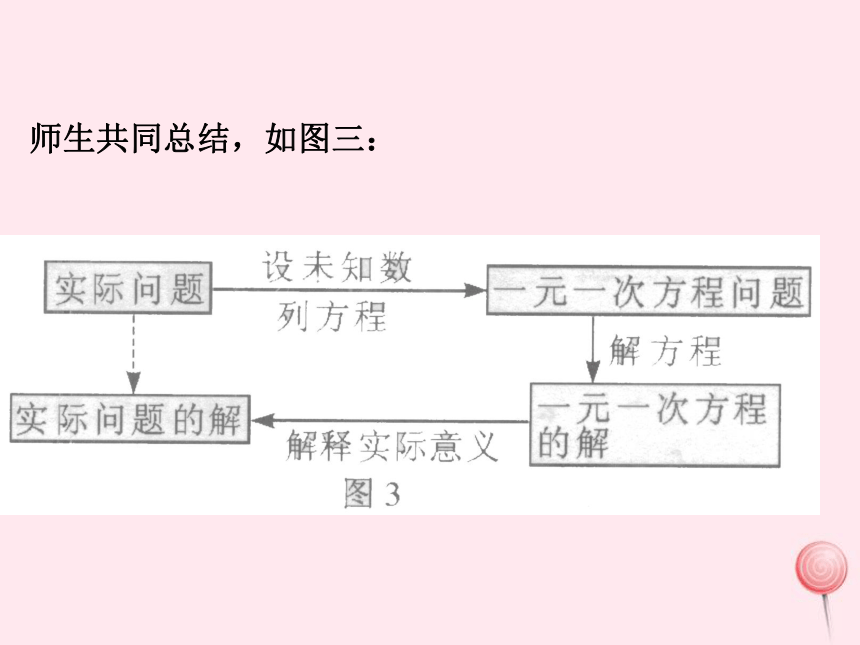
师生共同总结,如图2:
师生共同总结,如图三:
3.4.2 实际问题与一元一次方程
探究1 销售中的盈亏问题
跳楼价
?
“销售中的盈亏问题”
情境导入,激趣诱思
A. 盈利
B. 亏损
C. 不盈不亏
你估计盈亏情况是怎样的?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
提出问题,自主学习
展示交流:销售的盈亏决定于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系:
售价120 > 总成本
售价 120 < 总成本
售价 120 = 总成本
盈 利
亏 损
不盈不亏
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
展示成果,查找问题
合作探究计算:两件衣服的成本各是多少元?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分组学习,合作探究
合作探究计算:两件衣服的成本各是多少元?
(2)设亏损25%的衣服进价是 y元,
依题意得:y-0.25y=60
解得: y=80
分组学习,合作探究
(1)设盈利25%的衣服进价是 x 元,
依题意得:x+0.25 x=60
解得: x=48
解:
两件衣服总成本:x+y=48+80=128 元;
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
因为:120-128=-8元;
所以:卖这两件衣服共亏损了8元.
这个结论与你们组的猜想一致吗?
分组学习,合作探究
一件服装先将进价提高25%出售,后进行促销活动,又按标价的8折出售, 此时售价为60元. 请问商家是盈是亏,还是不盈不亏?
设:这件衣服的进价是x元,
则提价后的售价是(1+25%)x 元,
促销后的售价是(1+25%)x×0.8 元,
依题意得(1+25%)x×0.8=60
解得 x=60
精练精讲,重难突破
售价60=成本60
答:这家商店不盈不亏。
据了解个体商店销售中售价只要高出进价的20%便可盈利,但老板们常以高出进价50%~100%标价,假若你准备买一双标价为600元的运动鞋,应在什么范围内还价?
高于进价50% 高于进价100%
进价 x元 x元
标价 (1+50%)x (1+100%)x
方程 (1+50%)x=600 (1+100%)x=600
方程的解 x=400 x=300
盈利价 400(1+20%)=480 300(1+20%)=360
课堂练习,巩固基础
答:应在480元~360元内还价。
一台电视机进价为2000 元,若以 8 折
出售,仍可获利10%,求该电视机的标价.
解:设这该电视机的标价是x元,
则打折后的售价是0.8x元,
依题意得 0.8x=(1+10%)×2 000
解得 x=2 750
答:该电视机的标价为2 750元.
当堂评价,反馈深化
这节课你学习了哪些内容?
通过学习,你对方程在实际问题中的应用有什么新的认识?
师生共进,课堂小结
作业:
1.教科书第 106 页练习 1;
2.思考题:在本课探究的第一个问题中,假如你是商店老板,你能否设计一种方案,适当调整售价,使得销售这两件衣服时不亏本呢?
3.4.3 实际问题与一元一次方程
探究2 球赛积分表问题
情境导入,激趣诱思
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
某次篮球联赛积分榜如下::
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
问题1.你能从表格中
了解到哪些信息?
某次篮球联赛积分榜如下:
每队胜场总积分+负场
总积分=这个队的总积分;
每队的胜场数+负场数
=这个队比赛场次;
每队胜场总积分=
胜1场得分×胜场数; ……
提出问题,自主学习
某次篮球联赛积分榜如下:
问题2.你能从表格中看出负一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
由钢铁队得分可知负一场积1分。
提出问题,自主学习
某次篮球联赛积分榜如下:
问题3.你能进一步算出胜一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
设:胜一场积 x 分,
依题意,得
10x+1×4=24
解得: x=2
所以,胜一场积2分.
因为:从钢铁队得分已知负一场得1分,
所以:再观察其他任何一篮球队的得分
都能求出胜一场的得分.
提出问题,自主学习
问题4: 怎样用式子表示总积分与胜、负场数之间的关系.
解:若一个队胜m场,则负(14 – m)场,
总积分为: 2m+(14 – m) = m+14
即胜m场的总积分为 m +14 分。
展示成果,查找问题
问题2:从表格中看出负一场积1分;
问题3:能进一步算出胜一场积2分;
问题1:每队胜场总积分+负场总积分=这个队总积分; …
问题5:某队胜场总积分能等于它负场总积分吗?
解:设一个队胜x场,则负(14-x)场,
依题意得: 2x=14-x
解得: x=
想一想,x 表示什么量?它可以是分数吗?
分组学习,合作探究
所以:可判定没有哪个队的胜场总积分等于负场总积分。
注意:解决实际问题时,要考虑得到结果是不是符合实际。
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
队名 比赛场次 胜场 负场 积分
八一双鹿 22 18 4 40
北京首钢 22 14 8 36
浙江万马 22 7 15 29
沈部雄狮 22 0 22 22
课堂练习,巩固基础
解:观察积分榜,从最下面一行可知负一场积1分.
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得出方程:
18x+1×4=40.
由此得出 x=2.
得出:负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
课堂练习,巩固基础
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
? 依题意得: 2x=22-x
其中,x (胜场)的值必须是整数,所以 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
课堂练习,巩固基础
通过对球赛积分表的探究,你有什么收获?
2.解决有关表格问题,首先根据表格中给出的有关信息,找出数量间的关系,再运用数学知识解决有关问题.
3.利用方程不仅可以求得实际问题的具体数值,还可以进行推理判断.
4.运用方程解决实际问题,要检验方程的解是否符合实际意义.
1.生活中数据信息的传递形式是多种多样的.
师生共进,课堂小结
3.4.4 实际问题与一元一次方程
探究3 电话计费问题
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
情境导入,激趣诱思
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
提出问题,自主学习
350
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
展示成果,查找问题
350
“省钱方式与主叫时间有关”
活动1:设一个月内用移动电话主叫为t 分(t是正整数).根据t 在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
分组学习,合作探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 58+0.25(350-150)=108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
分组学习,合作探究
活动1:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
活动2:观察你的列表,你能从中发现如何根据主叫时间选择
省钱的计费方式吗?
划算
划算
划算
分组学习,合作探究
由上表可得:(1)当t ≤150时,方式一计费少;
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
解:依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
当 t =270分时,两种计费方式的费用相等;
当270< t <350时,方式二计费少;
分组学习,合作探究
活动2:
∴当150< t <270时,方式一计费 少;
(2)当150< t <350时,存在两种方式计费相等吗?
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(4)当t >350分时,两种计费方式哪种更合算呢?
分组学习,
合作探究
划算
(3)当t =350分时,方式二计费少;
活动2:
解:当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350)
方式二: 88+0.19(t-350)
所以:当t >350分时,方式二计费少;
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
当t
0
计费方式一
计费方式二
270
当 t 小于 270分
当 t 大于 270分
基本费58元
基本费88元
分组学习,合作探究
利用我们在“电话计费问题”中学会的方法,探
究下面的问题:
已知: 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
问:如何根据复印的页数选择复印的地点使总价格 比较便宜?(复印的页数不为零)
课堂练习,巩固基础
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,图书 馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
课堂练习,巩固基础
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,复印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,复印社价格便宜.
课堂练习,巩固基础
请回顾电话计费问题的探究过程,并回答
以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有
哪些收获?
师生共进,课堂小结
3.4.1 实际问题与一元一次方程
一、提出问题。
前面我们学习了一元一次方程的解法,本节课,我们讨论一元一次方程的应用。生活中,有很多需要进行配套的问题,如课桌和凳子、螺钉和螺母、电扇叶片和电机等,大家能举出生活中配套问题的例子吗?
例1.(教科书中例1)某车问有2 2名工人,每人每天可以生产1200个螺钉或2 000个螺母。 1个螺钉需要配2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少人?
二、解决问题,初步体会。
如图1:
三、变式训练
某车间有22名工人,每人每天可以生产1200个A部件或3000个B部件,一套机器由1个A部件和3个B部件构成,为使每天生产的A部件和B部件配套,应分别安排生产A、B部件各多少人?
例2. 一批螺钉和螺母需要打包,由一个人做40
小时才能完成。现计划由一部分人先做4小时,然后增加2人与他们一起做8小时,完成这项工作,假设这些人的工作效率相同,具体应先安排多少人参与这项工作?
四、解决问题,再次体会。
人均
效率 人数 时间 工作量
前一部分
工作 x 4
后一部分
工作 x+2 8
五、归纳总结,提炼思想。
师生共同总结,如图2:
师生共同总结,如图三:
3.4.2 实际问题与一元一次方程
探究1 销售中的盈亏问题
跳楼价
?
“销售中的盈亏问题”
情境导入,激趣诱思
A. 盈利
B. 亏损
C. 不盈不亏
你估计盈亏情况是怎样的?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
提出问题,自主学习
展示交流:销售的盈亏决定于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系:
售价120 > 总成本
售价 120 < 总成本
售价 120 = 总成本
盈 利
亏 损
不盈不亏
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
展示成果,查找问题
合作探究计算:两件衣服的成本各是多少元?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
分组学习,合作探究
合作探究计算:两件衣服的成本各是多少元?
(2)设亏损25%的衣服进价是 y元,
依题意得:y-0.25y=60
解得: y=80
分组学习,合作探究
(1)设盈利25%的衣服进价是 x 元,
依题意得:x+0.25 x=60
解得: x=48
解:
两件衣服总成本:x+y=48+80=128 元;
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏?
因为:120-128=-8元;
所以:卖这两件衣服共亏损了8元.
这个结论与你们组的猜想一致吗?
分组学习,合作探究
一件服装先将进价提高25%出售,后进行促销活动,又按标价的8折出售, 此时售价为60元. 请问商家是盈是亏,还是不盈不亏?
设:这件衣服的进价是x元,
则提价后的售价是(1+25%)x 元,
促销后的售价是(1+25%)x×0.8 元,
依题意得(1+25%)x×0.8=60
解得 x=60
精练精讲,重难突破
售价60=成本60
答:这家商店不盈不亏。
据了解个体商店销售中售价只要高出进价的20%便可盈利,但老板们常以高出进价50%~100%标价,假若你准备买一双标价为600元的运动鞋,应在什么范围内还价?
高于进价50% 高于进价100%
进价 x元 x元
标价 (1+50%)x (1+100%)x
方程 (1+50%)x=600 (1+100%)x=600
方程的解 x=400 x=300
盈利价 400(1+20%)=480 300(1+20%)=360
课堂练习,巩固基础
答:应在480元~360元内还价。
一台电视机进价为2000 元,若以 8 折
出售,仍可获利10%,求该电视机的标价.
解:设这该电视机的标价是x元,
则打折后的售价是0.8x元,
依题意得 0.8x=(1+10%)×2 000
解得 x=2 750
答:该电视机的标价为2 750元.
当堂评价,反馈深化
这节课你学习了哪些内容?
通过学习,你对方程在实际问题中的应用有什么新的认识?
师生共进,课堂小结
作业:
1.教科书第 106 页练习 1;
2.思考题:在本课探究的第一个问题中,假如你是商店老板,你能否设计一种方案,适当调整售价,使得销售这两件衣服时不亏本呢?
3.4.3 实际问题与一元一次方程
探究2 球赛积分表问题
情境导入,激趣诱思
队名 比赛场次 胜场 负场 积分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
某次篮球联赛积分榜如下::
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
问题1.你能从表格中
了解到哪些信息?
某次篮球联赛积分榜如下:
每队胜场总积分+负场
总积分=这个队的总积分;
每队的胜场数+负场数
=这个队比赛场次;
每队胜场总积分=
胜1场得分×胜场数; ……
提出问题,自主学习
某次篮球联赛积分榜如下:
问题2.你能从表格中看出负一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
由钢铁队得分可知负一场积1分。
提出问题,自主学习
某次篮球联赛积分榜如下:
问题3.你能进一步算出胜一场积多少分吗?
队名 比赛
场次 胜
场 负
场 积
分
前进 14 10 4 24
东方 14 10 4 24
光明 14 9 5 23
蓝天 14 9 5 23
雄鹰 14 7 7 21
远大 14 7 7 21
卫星 14 4 10 18
钢铁 14 0 14 14
设:胜一场积 x 分,
依题意,得
10x+1×4=24
解得: x=2
所以,胜一场积2分.
因为:从钢铁队得分已知负一场得1分,
所以:再观察其他任何一篮球队的得分
都能求出胜一场的得分.
提出问题,自主学习
问题4: 怎样用式子表示总积分与胜、负场数之间的关系.
解:若一个队胜m场,则负(14 – m)场,
总积分为: 2m+(14 – m) = m+14
即胜m场的总积分为 m +14 分。
展示成果,查找问题
问题2:从表格中看出负一场积1分;
问题3:能进一步算出胜一场积2分;
问题1:每队胜场总积分+负场总积分=这个队总积分; …
问题5:某队胜场总积分能等于它负场总积分吗?
解:设一个队胜x场,则负(14-x)场,
依题意得: 2x=14-x
解得: x=
想一想,x 表示什么量?它可以是分数吗?
分组学习,合作探究
所以:可判定没有哪个队的胜场总积分等于负场总积分。
注意:解决实际问题时,要考虑得到结果是不是符合实际。
2000赛季篮球甲A联赛部分球队积分榜:
(1)列式表示积分与胜、负场数之间的数量关系;
(2)某队的胜场总积分能等于它的负场总积分吗?
队名 比赛场次 胜场 负场 积分
八一双鹿 22 18 4 40
北京首钢 22 14 8 36
浙江万马 22 7 15 29
沈部雄狮 22 0 22 22
课堂练习,巩固基础
解:观察积分榜,从最下面一行可知负一场积1分.
设胜一场积x分,从表中其他任何一行可以列方程,求出x的值.例如,从第一行得出方程:
18x+1×4=40.
由此得出 x=2.
得出:负一场积1分,胜一场积2分.
(1)如果一个队胜m场,则负(22-m)场,胜场积分为2m,负场积分为22-m,总积分为
2m+(22-m)=m+22.
课堂练习,巩固基础
(2)设一个队胜了x场,则负了(22-x)场,如果这个队的胜场总积分等于负场总积分,则有方程
? 依题意得: 2x=22-x
其中,x (胜场)的值必须是整数,所以 不符合实际.由此可以判定没有哪个队伍的胜场总积分等于负场总积分.
课堂练习,巩固基础
通过对球赛积分表的探究,你有什么收获?
2.解决有关表格问题,首先根据表格中给出的有关信息,找出数量间的关系,再运用数学知识解决有关问题.
3.利用方程不仅可以求得实际问题的具体数值,还可以进行推理判断.
4.运用方程解决实际问题,要检验方程的解是否符合实际意义.
1.生活中数据信息的传递形式是多种多样的.
师生共进,课堂小结
3.4.4 实际问题与一元一次方程
探究3 电话计费问题
下表给出的是两种移动电话的计费方式:
免费
0.19
350
88
方式二
免费
0.25
150
58
方式一
被叫
主叫超时费(元/分)
主叫限定时间(分)
月使用
费(元)
你了解表格中这些数字的含义吗?
情境导入,激趣诱思
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
提出问题,自主学习
350
你认为选择以下哪种计费方式更省钱呢?
350
0
加超时费0.19元/分
基本费88元
加超时费0.25元/分
基本费58元
150
计费方式一
计费方式二
展示成果,查找问题
350
“省钱方式与主叫时间有关”
活动1:设一个月内用移动电话主叫为t 分(t是正整数).根据t 在不同时间范围内取值,列表说明按方式一和方式二如何计费.
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150
t 等于150
t 大于150且小于 350
t 等于350
t 大于350
分组学习,合作探究
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 58+0.25(350-150)=108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
分组学习,合作探究
活动1:
主叫时间t /分 方式一计费/元 方式二计费/元
t 小于150 58 88
t 等于150 58 88
t 大于150且小于 350 58+0.25(t-150) 88
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
活动2:观察你的列表,你能从中发现如何根据主叫时间选择
省钱的计费方式吗?
划算
划算
划算
分组学习,合作探究
由上表可得:(1)当t ≤150时,方式一计费少;
主叫时间t /分 方式一计费/元 方式二计费/元
t 大于150且小于 350 58+0.25(t-150) 88
解:依题意得: 58+0.25(t-150) = 88
去括号得: 58+0.25t-37.5 = 88
移项、合并同类项得: 0.25t = 67.5
系数化1得: t =270
当 t =270分时,两种计费方式的费用相等;
当270< t <350时,方式二计费少;
分组学习,合作探究
活动2:
∴当150< t <270时,方式一计费 少;
(2)当150< t <350时,存在两种方式计费相等吗?
主叫时间t /分 方式一计费/元 方式二计费/元
t 等于350 108 88
t 大于350 58+0.25(t-150) 88+0.19(t-350)
(4)当t >350分时,两种计费方式哪种更合算呢?
分组学习,
合作探究
划算
(3)当t =350分时,方式二计费少;
活动2:
解:当t >350时,
方式一: 58+0.25(t-150)= 108+0.25(t-350)
方式二: 88+0.19(t-350)
所以:当t >350分时,方式二计费少;
综合以上的分析,可以发现:
时,选择方式一省钱;
时,选择方式二省钱.
当t
0
计费方式一
计费方式二
270
当 t 小于 270分
当 t 大于 270分
基本费58元
基本费88元
分组学习,合作探究
利用我们在“电话计费问题”中学会的方法,探
究下面的问题:
已知: 用A4纸在某复印社复印文件,复印页数不超过20时每页收费0.12元;复印页数超过20页时,超过部分每页收费0.09元. 在某图书馆复印同样的文件,不论复印多少页,每页收费0.1元.
问:如何根据复印的页数选择复印的地点使总价格 比较便宜?(复印的页数不为零)
课堂练习,巩固基础
复印页数x 复印社复印费用/元 图书馆复印费用/元
x 小于20 0.12x 0.1x
x 等于20 0.12×20=2.4 0.1×20=2
x 大于20 2.4+0.09(x-20) 0.1x
解:依题意列表得:
(1)当 x 小于20时,0.12 x大于0.1 x恒成立,图书 馆价格便宜;
(2)当 x 等于20时,2.4大于2,图书馆价格便宜;
课堂练习,巩固基础
(3)当 x 大于20时,
依题意得:2.4+0.09(x-20)=0.1x
解得: x=60
∴ 当x大于20且小于60时,图书馆价格便宜;
当x大于60时,复印社价格便宜.
综上所述:当x小于60页时,图书馆价格便宜;
当x大于60时,复印社价格便宜.
课堂练习,巩固基础
请回顾电话计费问题的探究过程,并回答
以下问题:
(1)电话计费问题的核心问题是什么?
(2)探究解题的过程大致包含哪几个步骤?
(3)我们在探究过程中用到了哪些方法,你有
哪些收获?
师生共进,课堂小结
