北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第12讲 圆的有关概念及圆的确定含答案
文档属性
| 名称 | 北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第12讲 圆的有关概念及圆的确定含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 256.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 00:00:00 | ||
图片预览


文档简介
圆的有关概念及圆的确定—知识讲解
【学习目标】
1.知识目标:理解圆的描述概念和圆的集合概念;理解半径、直径、弧、弦、弦心距、圆心角、同心圆、等圆、等弧的概念;经历探索点与圆的位置关系的过程,会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系;了解不在同一直线上的三点确定一个圆,了解三角形的外接圆、三角形的外心、圆的外接三角形的概念.
2.能力目标:能应用圆半径、直径、弧、弦、弦心距的关系,进行计算或证明;会过不在同一直线上的三点作圆.
3.情感目标:在确定点和圆的三种位置关系的过程中体会用数量关系来确定位置关系的方法,逐步学会用变化的观点及思想去解决问题,养成学生之间发现问题、探讨问题、解决问题的习惯.
【要点梳理】
要点一、圆的定义
1. 圆的描述概念
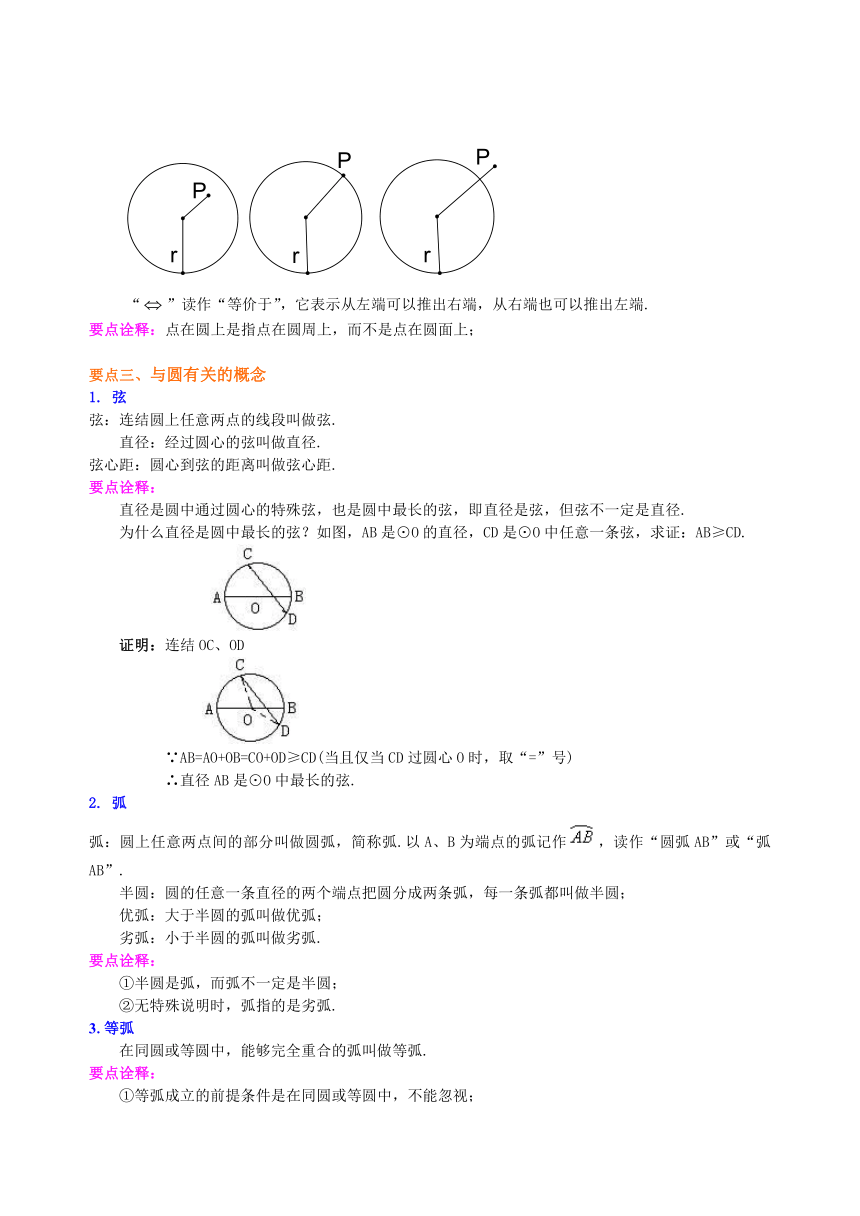
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径. 以点O为圆心的圆,记作“⊙O”,读作“圆O”. 要点诠释: ①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可; ②圆是一条封闭曲线.
2.圆的集合概念
圆心为O,半径为r的圆是平面内到定点O的距离等于定长r的点的集合. 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看作是到圆心的距离小于半径的的点的集合;圆的外部可以看成是到圆心的距离大于半径的点的集合.
要点诠释: ①定点为圆心,定长为半径; ②圆指的是圆周,而不是圆面; ③强调“在一个平面内”是非常必要的,事实上,在空间中,到定点的距离等于定长的点的集合是球面,一个闭合的曲面.
要点二、点与圆的位置关系
点和圆的位置关系有三种:点在圆内,点在圆上,点在圆外.
若⊙O的半径为r,点P到圆心O的距离为d,那么:
点P在圆内 d < r ;
点P在圆上 d = r ;
点P在圆外 d >r.
“”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端.
要点诠释:点在圆上是指点在圆周上,而不是点在圆面上;
要点三、与圆有关的概念
1. 弦
弦:连结圆上任意两点的线段叫做弦. 直径:经过圆心的弦叫做直径.
弦心距:圆心到弦的距离叫做弦心距. 要点诠释: 直径是圆中通过圆心的特殊弦,也是圆中最长的弦,即直径是弦,但弦不一定是直径. 为什么直径是圆中最长的弦?如图,AB是⊙O的直径,CD是⊙O中任意一条弦,求证:AB≥CD. 证明:连结OC、OD ∵AB=AO+OB=CO+OD≥CD(当且仅当CD过圆心O时,取“=”号) ∴直径AB是⊙O中最长的弦. 2. 弧 弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作,读作“圆弧AB”或“弧AB”. 半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆; 优弧:大于半圆的弧叫做优弧; 劣弧:小于半圆的弧叫做劣弧. 要点诠释: ①半圆是弧,而弧不一定是半圆; ②无特殊说明时,弧指的是劣弧. 3.等弧 在同圆或等圆中,能够完全重合的弧叫做等弧. 要点诠释: ①等弧成立的前提条件是在同圆或等圆中,不能忽视; ②圆中两平行弦所夹的弧相等.
4.同心圆与等圆 圆心相同,半径不等的两个圆叫做同心圆. 圆心不同,半径相等的两个圆叫做等圆.
要点诠释:同圆或等圆的半径相等.
5.圆心角
顶点在圆心的角叫做圆心角.
要点诠释:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,反之也成立.
要点四、确定圆的条件
(1)经过一个已知点能作无数个圆;
(2)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(3)不在同一直线上的三个点确定一个圆.
(4)经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
外心的性质:外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
要点诠释:
(1)不在同一直线上的三个点确定一个圆.“确定”的含义是“存在性和唯一性”.
(2)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
【典型例题】
类型一、圆的定义
1.(2019秋?邳州市校级月考)如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
【思路点拨】要证几个点在同一个圆上,就是证明这几个点到同一点的距离都相等即可.
【答案与解析】
证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
【总结升华】要证几个点在同一个圆上,只能依据圆的定义,去说明这些点到平面内某一点的距离相等.
举一反三:
【变式】平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )
A.正方形 B.菱形 C.矩形 D.等腰梯形
【答案】C.
2. 爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域.这个导火索的长度为18cm,那么点导火索的人每秒钟跑6.5m是否安全?
【思路点拨】计算在导火索燃烧完的时间内人跑的距离与120m比较.
【答案与解析】
∵导火索燃烧的时间为
相同时间内,人跑的路程为20×6.5=130(m)
∴人跑的路程为130m>120m,
∴点导火索的人安全.
【总结升华】爆破时的安全区域是以爆破点为圆心,以120m为半径的圆的外部,如图所示.
类型二、圆的有关计算
3.已知,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有的⊙O的弦中,弦长为整数的弦的条数为( ) A.2 B.3 C.4 D.5
【思路点拨】
在一个圆中,过一点的最长弦是经过这一点的直径,最短的弦是经过这一点与直径垂直的弦.
【答案】 C.
【解析】作图,过点P作直径AB,过点P作弦,连接OC
则OC=5,CD=2PC, 由勾股定理,得, ∴CD=2PC=8,又∵AB=10, ∴过点P的弦长的取值范围是,
弦长的整数解为8,9,10,根据圆的对称性,弦长为9的弦有两条,所以弦长为整数的弦共4 条. 故选C.
【总结升华】利用垂径定理来确定过点P的弦长的取值范围.根据圆的对称性,弦长为9的弦有两条,容易漏解.
举一反三:
【变式】平面上的一个点到圆的最小距离是4cm,最大距离是9cm,则圆的半径是( ).
A.2.5cm B.6.5cm C. 2.5cm或6.5cm D. 5cm或13cm
【答案】C.
类型三、确定圆的条件的有关作图与计算
4.已知:不在同一直线上的三点A、B、C,求作: ⊙O使它经过点A、B、C.
【思路点拨】作圆的关键是找圆心得位置及半径的大小,经过两点的圆的圆心一定在连接这两点的线段的垂直平分线上,进而可以作出经过不在同一直线上的三点的圆.
【解析】
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.
【总结升华】通过这个例题的作图可以作出锐角三角形的外心(图一),直角三角形的外心(图二),钝角三角形的外心(图三).探究各自外心的位置.
【变式】(2019?江干区二模)给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径
C.已知直径 D. 不在同一直线上的三个点
【答案】D.
提示:A、已知圆心只能确定圆的位置不能确定圆的大小,故错误;
B、C、已知圆的半径和直径只能确定圆的大小并不能确定圆的位置,故错误;
D、不在同一直线上的三点确定一个圆,故正确,
故选D.
5.如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 .
【思路点拨】求出符合条件的OP的最大值与最小值.
【答案】3≤OP≤5.
【解析】OP最长边应是半径长,为5;
根据垂线段最短,可得到当OP⊥AB时,OP最短.
∵直径为10,弦AB=8
∴∠OPA=90°,OA=5,由圆的对称性得AP=4,
由勾股定理的OP=,∴OP最短为3.
∴OP的长的取值范围是3≤OP≤5.
【总结升华】关键是知道OP何时最长与最短.
举一反三:
【变式】已知⊙O的半径为13,弦AB=24,P是弦AB上的一个动点,则OP的取值范围是___ ____.
【答案】 OP最大为半径,最小为O到AB的距离.所以5≤OP≤13.
圆的有关概念及圆的确定—巩固练习
【巩固练习】
一、选择题
1.(2019春?张掖校级月考)有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )
A.1 B. 2 C. 3 D. 4
2.下列语句中,不正确的个数是( )
①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
3.如图,⊙O中,点A、O、D以及点B、O、C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
第3题 第4题
4.如图,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A.1个 B.2个 C.3个 D.4个
5.已知:A,B,C,D,E五个点中无任何三点共线,无任何四点共圆,那么过其中的三点作圆,最多能作出( ).
A.5个圆 B.8个圆 C.10个圆 D.12个圆
6. 如图,点A 、D、G、M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,NH=c,
则下列各式正确的是( )
A.a>b>c B.b>c>a C.c>a>b D.a=b=c
第6题 第7题
二、填空题
7.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y都是整数,猜想这样的P点一共有 .
8.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.
9.(2019春?定陶县期末)下列说法正确的是 (填序号).
①半径不等的圆叫做同心圆; ②优弧一定大于劣弧;
③不同的圆中不可能有相等的弦; ④直径是同一个圆中最长的弦.
10.如图,在半径不等的同心圆中,圆心角∠AOB所对的的长度有__ ___关系;的度数有_ ___关系.
11.如图,已知⊙O内一点P,过P点的最短的弦在圆内的位置是__ __;
过P点的最长的弦在圆内的位置是__ __;并分别将图画出来.
12.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,……
(1)10个圆把平面最多分成 个部分;
(2)n个圆把平面最多分成 个部分.
三、解答题
13.已知⊙O的半径r=5cm,圆心O到直线的距离d=OD=3cm,在直线上有P、Q、R三点,
且有PD=4cm,QD>4cm,RD<4cm,P、Q、R三点与⊙O位置关系各是怎样的?
14.(2019秋?江宁区校级期中)如图,BD=OD,∠AOC=114°,求∠AOD的度数.
15.如图所示,AB是⊙O的一条弦(不是直径),点C,D是直线AB上的两点,且AC=BD.
(1)判断△OCD的形状,并说明理由.
(2)当图中的点C与点D在线段AB上时(即C,D在A,B两点之间),(1)题的结论还存在吗?
【答案与解析】
一、选择题
1.【答案】B;
【解析】①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.其中错误说法的是①③两个.故选:B.
2.【答案】C;
【解析】①直径是弦符合弦的定义正确;②弧是半圆,这句话不对,可能是半圆,也可能使优弧或劣弧;③长度相等的弧是等弧,这句话不符合等弧的定义:能够完全重合的弧,故错误;④经过圆内一定点只能作一条直径.所以原题不正确. 故②③④都不正确.
3.【答案】B;
【解析】图中的弦有弦AB、弦BC、弦CE共三条.
4.【答案】C;
【解析】在弦AB所在直线的两侧分别有1个和两个点符合要求,故选C;
5.【答案】C.
【解析】过其中的三点作圆,最多能作出10个,即分别过点ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE的圆.
6.【答案】D;
【解析】如图,连接OM、OD、OA、根据矩形的对角线相等,得BC=OA,EF=OD,NH=OM.再根据同圆的半径相等,得a=b=c.故选D;
二、填空题
7.【答案】12.
【解析】每个象限有2个符合要求的点,坐标轴上有4个点,共12个.
即:(3,4)、(4,3)、(3,-4)、(4,-3)、(-3,4)、(-4,3)、
(-3,-4)、(-4,-3)、?(0,5)、(0,-5)、(5,0)、(-5,0).
8.【答案】26cm;
9.【答案】④;
【解析】①半径不等的圆叫做同心圆,错误;
②优弧一定大于劣弧,错误;
③不同的圆中不可能有相等的弦,错误;
④直径是同一个圆中最长的弦,正确.
故答案为:④.
10.【答案】;相等;
11.【答案】垂直于过p点的直径的弦;过p点的直径. 如图:
12.【答案】(1)92; (2)n2-n+2.
【解析】(1)9×10+2=92;(2)(n-1)n+2=n2-n+2.
三、解答题
13.【答案与解析】
依题意画出图形(如图所示),计算出P、Q、R三点到圆心的距离与圆的半径比较大小.
连接PO,QO,RO.
∵ PD=4cm,OD=3cm,
∴ PO=.
∴ 点P在⊙O上.
,
∴ 点Q在⊙O外.
,
∴ 点R在⊙O内.
14.【答案与解析】
解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
15.【答案与解析】
(1)△OCD是等腰三角形.
如图(1)所示,过点O作OM⊥AB,垂足为M,由圆的对称性有MA=MB.
又∵AC=BD,
∴AC+MA=BD+MB, 即CM=DM.
又OM⊥CD,即OM是CD的垂直平分线,
∴OC=OD,
∴△OCD为等腰三角形.
(1) (2)
(2)当点C,D在线段AB上时,(1)题的结论还存在.
如图(2)所示,
同上问,作OM⊥AB,垂足为M,
由圆的对称性,得AM=BM.
又∵AC=BD,
∴CM=AM-AC=BM-BD=DM,
∴OC=OD,
∴△OCD为等腰三角形.
【学习目标】
1.知识目标:理解圆的描述概念和圆的集合概念;理解半径、直径、弧、弦、弦心距、圆心角、同心圆、等圆、等弧的概念;经历探索点与圆的位置关系的过程,会运用点到圆心的距离与圆的半径之间的数量关系判断点与圆的位置关系;了解不在同一直线上的三点确定一个圆,了解三角形的外接圆、三角形的外心、圆的外接三角形的概念.
2.能力目标:能应用圆半径、直径、弧、弦、弦心距的关系,进行计算或证明;会过不在同一直线上的三点作圆.
3.情感目标:在确定点和圆的三种位置关系的过程中体会用数量关系来确定位置关系的方法,逐步学会用变化的观点及思想去解决问题,养成学生之间发现问题、探讨问题、解决问题的习惯.
【要点梳理】
要点一、圆的定义
1. 圆的描述概念
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,另一个端点A随之旋转所形成的图形叫做圆,固定的端点O叫做圆心,线段OA叫做半径. 以点O为圆心的圆,记作“⊙O”,读作“圆O”. 要点诠释: ①圆心确定圆的位置,半径确定圆的大小;确定一个圆应先确定圆心,再确定半径,二者缺一不可; ②圆是一条封闭曲线.
2.圆的集合概念
圆心为O,半径为r的圆是平面内到定点O的距离等于定长r的点的集合. 平面上的一个圆,把平面上的点分成三类:圆上的点,圆内的点和圆外的点.
圆的内部可以看作是到圆心的距离小于半径的的点的集合;圆的外部可以看成是到圆心的距离大于半径的点的集合.
要点诠释: ①定点为圆心,定长为半径; ②圆指的是圆周,而不是圆面; ③强调“在一个平面内”是非常必要的,事实上,在空间中,到定点的距离等于定长的点的集合是球面,一个闭合的曲面.
要点二、点与圆的位置关系
点和圆的位置关系有三种:点在圆内,点在圆上,点在圆外.
若⊙O的半径为r,点P到圆心O的距离为d,那么:
点P在圆内 d < r ;
点P在圆上 d = r ;
点P在圆外 d >r.
“”读作“等价于”,它表示从左端可以推出右端,从右端也可以推出左端.
要点诠释:点在圆上是指点在圆周上,而不是点在圆面上;
要点三、与圆有关的概念
1. 弦
弦:连结圆上任意两点的线段叫做弦. 直径:经过圆心的弦叫做直径.
弦心距:圆心到弦的距离叫做弦心距. 要点诠释: 直径是圆中通过圆心的特殊弦,也是圆中最长的弦,即直径是弦,但弦不一定是直径. 为什么直径是圆中最长的弦?如图,AB是⊙O的直径,CD是⊙O中任意一条弦,求证:AB≥CD. 证明:连结OC、OD ∵AB=AO+OB=CO+OD≥CD(当且仅当CD过圆心O时,取“=”号) ∴直径AB是⊙O中最长的弦. 2. 弧 弧:圆上任意两点间的部分叫做圆弧,简称弧.以A、B为端点的弧记作,读作“圆弧AB”或“弧AB”. 半圆:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆; 优弧:大于半圆的弧叫做优弧; 劣弧:小于半圆的弧叫做劣弧. 要点诠释: ①半圆是弧,而弧不一定是半圆; ②无特殊说明时,弧指的是劣弧. 3.等弧 在同圆或等圆中,能够完全重合的弧叫做等弧. 要点诠释: ①等弧成立的前提条件是在同圆或等圆中,不能忽视; ②圆中两平行弦所夹的弧相等.
4.同心圆与等圆 圆心相同,半径不等的两个圆叫做同心圆. 圆心不同,半径相等的两个圆叫做等圆.
要点诠释:同圆或等圆的半径相等.
5.圆心角
顶点在圆心的角叫做圆心角.
要点诠释:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,反之也成立.
要点四、确定圆的条件
(1)经过一个已知点能作无数个圆;
(2)经过两个已知点A、B能作无数个圆,这些圆的圆心在线段AB的垂直平分线上;
(3)不在同一直线上的三个点确定一个圆.
(4)经过三角形各个顶点的圆叫做三角形的外接圆,外接圆的圆心叫做三角形的外心,这个三角形叫做圆的内接三角形.
如图:⊙O是△ABC的外接圆, △ABC是⊙O的内接三角形,点O是△ABC的外心.
外心的性质:外心是△ABC三条边的垂直平分线的交点,它到三角形的三个顶点的距离相等.
要点诠释:
(1)不在同一直线上的三个点确定一个圆.“确定”的含义是“存在性和唯一性”.
(2)只有确定了圆心和圆的半径,这个圆的位置和大小才唯一确定.
【典型例题】
类型一、圆的定义
1.(2019秋?邳州市校级月考)如图所示,BD,CE是△ABC的高,求证:E,B,C,D四点在同一个圆上.
【思路点拨】要证几个点在同一个圆上,就是证明这几个点到同一点的距离都相等即可.
【答案与解析】
证明:如图所示,取BC的中点F,连接DF,EF.
∵BD,CE是△ABC的高,
∴△BCD和△BCE都是直角三角形.
∴DF,EF分别为Rt△BCD和Rt△BCE斜边上的中线,
∴DF=EF=BF=CF.
∴E,B,C,D四点在以F点为圆心,BC为半径的圆上.
【总结升华】要证几个点在同一个圆上,只能依据圆的定义,去说明这些点到平面内某一点的距离相等.
举一反三:
【变式】平行四边形的四个顶点在同一圆上,则该平行四边形一定是( )
A.正方形 B.菱形 C.矩形 D.等腰梯形
【答案】C.
2. 爆破时,导火索燃烧的速度是每秒0.9cm,点导火索的人需要跑到离爆破点120m以外的安全区域.这个导火索的长度为18cm,那么点导火索的人每秒钟跑6.5m是否安全?
【思路点拨】计算在导火索燃烧完的时间内人跑的距离与120m比较.
【答案与解析】
∵导火索燃烧的时间为
相同时间内,人跑的路程为20×6.5=130(m)
∴人跑的路程为130m>120m,
∴点导火索的人安全.
【总结升华】爆破时的安全区域是以爆破点为圆心,以120m为半径的圆的外部,如图所示.
类型二、圆的有关计算
3.已知,点P是半径为5的⊙O内一点,且OP=3,在过点P的所有的⊙O的弦中,弦长为整数的弦的条数为( ) A.2 B.3 C.4 D.5
【思路点拨】
在一个圆中,过一点的最长弦是经过这一点的直径,最短的弦是经过这一点与直径垂直的弦.
【答案】 C.
【解析】作图,过点P作直径AB,过点P作弦,连接OC
则OC=5,CD=2PC, 由勾股定理,得, ∴CD=2PC=8,又∵AB=10, ∴过点P的弦长的取值范围是,
弦长的整数解为8,9,10,根据圆的对称性,弦长为9的弦有两条,所以弦长为整数的弦共4 条. 故选C.
【总结升华】利用垂径定理来确定过点P的弦长的取值范围.根据圆的对称性,弦长为9的弦有两条,容易漏解.
举一反三:
【变式】平面上的一个点到圆的最小距离是4cm,最大距离是9cm,则圆的半径是( ).
A.2.5cm B.6.5cm C. 2.5cm或6.5cm D. 5cm或13cm
【答案】C.
类型三、确定圆的条件的有关作图与计算
4.已知:不在同一直线上的三点A、B、C,求作: ⊙O使它经过点A、B、C.
【思路点拨】作圆的关键是找圆心得位置及半径的大小,经过两点的圆的圆心一定在连接这两点的线段的垂直平分线上,进而可以作出经过不在同一直线上的三点的圆.
【解析】
作法:
1、连结AB,作线段AB的垂直平分线MN;
2、连接AC,作线段AC的垂直平分线EF,交MN于点O;
3、以O为圆心,OB为半径作圆.
所以⊙O就是所求作的圆.
【总结升华】通过这个例题的作图可以作出锐角三角形的外心(图一),直角三角形的外心(图二),钝角三角形的外心(图三).探究各自外心的位置.
【变式】(2019?江干区二模)给定下列图形可以确定一个圆的是( )
A.已知圆心 B. 已知半径
C.已知直径 D. 不在同一直线上的三个点
【答案】D.
提示:A、已知圆心只能确定圆的位置不能确定圆的大小,故错误;
B、C、已知圆的半径和直径只能确定圆的大小并不能确定圆的位置,故错误;
D、不在同一直线上的三点确定一个圆,故正确,
故选D.
5.如图,⊙O的直径为10,弦AB=8,P是弦AB上的一个动点,那么OP的长的取值范围是 .
【思路点拨】求出符合条件的OP的最大值与最小值.
【答案】3≤OP≤5.
【解析】OP最长边应是半径长,为5;
根据垂线段最短,可得到当OP⊥AB时,OP最短.
∵直径为10,弦AB=8
∴∠OPA=90°,OA=5,由圆的对称性得AP=4,
由勾股定理的OP=,∴OP最短为3.
∴OP的长的取值范围是3≤OP≤5.
【总结升华】关键是知道OP何时最长与最短.
举一反三:
【变式】已知⊙O的半径为13,弦AB=24,P是弦AB上的一个动点,则OP的取值范围是___ ____.
【答案】 OP最大为半径,最小为O到AB的距离.所以5≤OP≤13.
圆的有关概念及圆的确定—巩固练习
【巩固练习】
一、选择题
1.(2019春?张掖校级月考)有下列四个说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中错误说法的个数是( )
A.1 B. 2 C. 3 D. 4
2.下列语句中,不正确的个数是( )
①直径是弦;②弧是半圆;③长度相等的弧是等弧;④经过圆内一定点可以作无数条直径.
A.1个 B.2个 C.3个 D.4个
3.如图,⊙O中,点A、O、D以及点B、O、C分别在一条直线上,图中弦的条数有( )
A.2条 B.3条 C.4条 D.5条
第3题 第4题
4.如图,已知⊙O的半径为5,点O到弦AB的距离为3,则⊙O上到弦AB所在直线的距离为2的点有( )
A.1个 B.2个 C.3个 D.4个
5.已知:A,B,C,D,E五个点中无任何三点共线,无任何四点共圆,那么过其中的三点作圆,最多能作出( ).
A.5个圆 B.8个圆 C.10个圆 D.12个圆
6. 如图,点A 、D、G、M在半圆O上,四边形ABOC,DEOF,HMNO均为矩形,设BC=a,EF=b,NH=c,
则下列各式正确的是( )
A.a>b>c B.b>c>a C.c>a>b D.a=b=c
第6题 第7题
二、填空题
7.如图,P(x,y)是以坐标原点为圆心,5为半径的圆周上的点,若x、y都是整数,猜想这样的P点一共有 .
8.若△ABC中,∠C=90°,AC=10cm,BC=24cm,则它的外接圆的直径为___________.
9.(2019春?定陶县期末)下列说法正确的是 (填序号).
①半径不等的圆叫做同心圆; ②优弧一定大于劣弧;
③不同的圆中不可能有相等的弦; ④直径是同一个圆中最长的弦.
10.如图,在半径不等的同心圆中,圆心角∠AOB所对的的长度有__ ___关系;的度数有_ ___关系.
11.如图,已知⊙O内一点P,过P点的最短的弦在圆内的位置是__ __;
过P点的最长的弦在圆内的位置是__ __;并分别将图画出来.
12.在同一平面内,1个圆把平面分成0×1+2=2个部分,2个圆把平面最多分成1×2+2=4个部分,,3个圆把平面最多分成2×3+2=8个部分,4个圆把平面最多分成3×4+2=14个部分,……
(1)10个圆把平面最多分成 个部分;
(2)n个圆把平面最多分成 个部分.
三、解答题
13.已知⊙O的半径r=5cm,圆心O到直线的距离d=OD=3cm,在直线上有P、Q、R三点,
且有PD=4cm,QD>4cm,RD<4cm,P、Q、R三点与⊙O位置关系各是怎样的?
14.(2019秋?江宁区校级期中)如图,BD=OD,∠AOC=114°,求∠AOD的度数.
15.如图所示,AB是⊙O的一条弦(不是直径),点C,D是直线AB上的两点,且AC=BD.
(1)判断△OCD的形状,并说明理由.
(2)当图中的点C与点D在线段AB上时(即C,D在A,B两点之间),(1)题的结论还存在吗?
【答案与解析】
一、选择题
1.【答案】B;
【解析】①圆确定的条件是确定圆心与半径,是假命题,故此说法错误;
②直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;
③弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;
④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.其中错误说法的是①③两个.故选:B.
2.【答案】C;
【解析】①直径是弦符合弦的定义正确;②弧是半圆,这句话不对,可能是半圆,也可能使优弧或劣弧;③长度相等的弧是等弧,这句话不符合等弧的定义:能够完全重合的弧,故错误;④经过圆内一定点只能作一条直径.所以原题不正确. 故②③④都不正确.
3.【答案】B;
【解析】图中的弦有弦AB、弦BC、弦CE共三条.
4.【答案】C;
【解析】在弦AB所在直线的两侧分别有1个和两个点符合要求,故选C;
5.【答案】C.
【解析】过其中的三点作圆,最多能作出10个,即分别过点ABC、ABD、ABE、ACD、ACE、ADE、BCD、BCE、BDE、CDE的圆.
6.【答案】D;
【解析】如图,连接OM、OD、OA、根据矩形的对角线相等,得BC=OA,EF=OD,NH=OM.再根据同圆的半径相等,得a=b=c.故选D;
二、填空题
7.【答案】12.
【解析】每个象限有2个符合要求的点,坐标轴上有4个点,共12个.
即:(3,4)、(4,3)、(3,-4)、(4,-3)、(-3,4)、(-4,3)、
(-3,-4)、(-4,-3)、?(0,5)、(0,-5)、(5,0)、(-5,0).
8.【答案】26cm;
9.【答案】④;
【解析】①半径不等的圆叫做同心圆,错误;
②优弧一定大于劣弧,错误;
③不同的圆中不可能有相等的弦,错误;
④直径是同一个圆中最长的弦,正确.
故答案为:④.
10.【答案】;相等;
11.【答案】垂直于过p点的直径的弦;过p点的直径. 如图:
12.【答案】(1)92; (2)n2-n+2.
【解析】(1)9×10+2=92;(2)(n-1)n+2=n2-n+2.
三、解答题
13.【答案与解析】
依题意画出图形(如图所示),计算出P、Q、R三点到圆心的距离与圆的半径比较大小.
连接PO,QO,RO.
∵ PD=4cm,OD=3cm,
∴ PO=.
∴ 点P在⊙O上.
,
∴ 点Q在⊙O外.
,
∴ 点R在⊙O内.
14.【答案与解析】
解:设∠B=x,
∵BD=OD,
∴∠DOB=∠B=x,
∴∠ADO=∠DOB+∠B=2x,
∵OA=OD,
∴∠A=∠ADO=2x,
∵∠AOC=∠A+∠B,
∴2x+x=114°,解得x=38°,
∴∠AOD=180°﹣∠OAD﹣∠ADO=180°﹣4x=180°﹣4×38°=28°.
15.【答案与解析】
(1)△OCD是等腰三角形.
如图(1)所示,过点O作OM⊥AB,垂足为M,由圆的对称性有MA=MB.
又∵AC=BD,
∴AC+MA=BD+MB, 即CM=DM.
又OM⊥CD,即OM是CD的垂直平分线,
∴OC=OD,
∴△OCD为等腰三角形.
(1) (2)
(2)当点C,D在线段AB上时,(1)题的结论还存在.
如图(2)所示,
同上问,作OM⊥AB,垂足为M,
由圆的对称性,得AM=BM.
又∵AC=BD,
∴CM=AM-AC=BM-BD=DM,
∴OC=OD,
∴△OCD为等腰三角形.
