北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第16讲 切线长定理(含答案)
文档属性
| 名称 | 北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第16讲 切线长定理(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 196.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 00:00:00 | ||
图片预览



文档简介
切线长定理—知识讲解
【学习目标】
1.了解切线长定义,掌握切线长定理;
2.了解圆外切四边形定义及性质;
3. 利用切线长定理解决相关的计算和证明.
【要点梳理】
要点一、切线长定理 1.切线长: 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 要点诠释: 切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理: 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释: 切线长定理包含两个结论:线段相等和角相等.
要点二、圆外切四边形的性质
1.圆外切四边形
四边形的四条边都与同一个圆相切,那这个四边形叫做圆的外切四边形.
2.圆外切四边形性质
圆外切四边形的两组对边之和相等. 【典型例题】
类型一、切线长定理
1.(2019秋?湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
【答案与解析】
解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
【总结升华】本题考查的是切线长定理和全等三角形的判定和性质,掌握切线长定理是解题的关键.
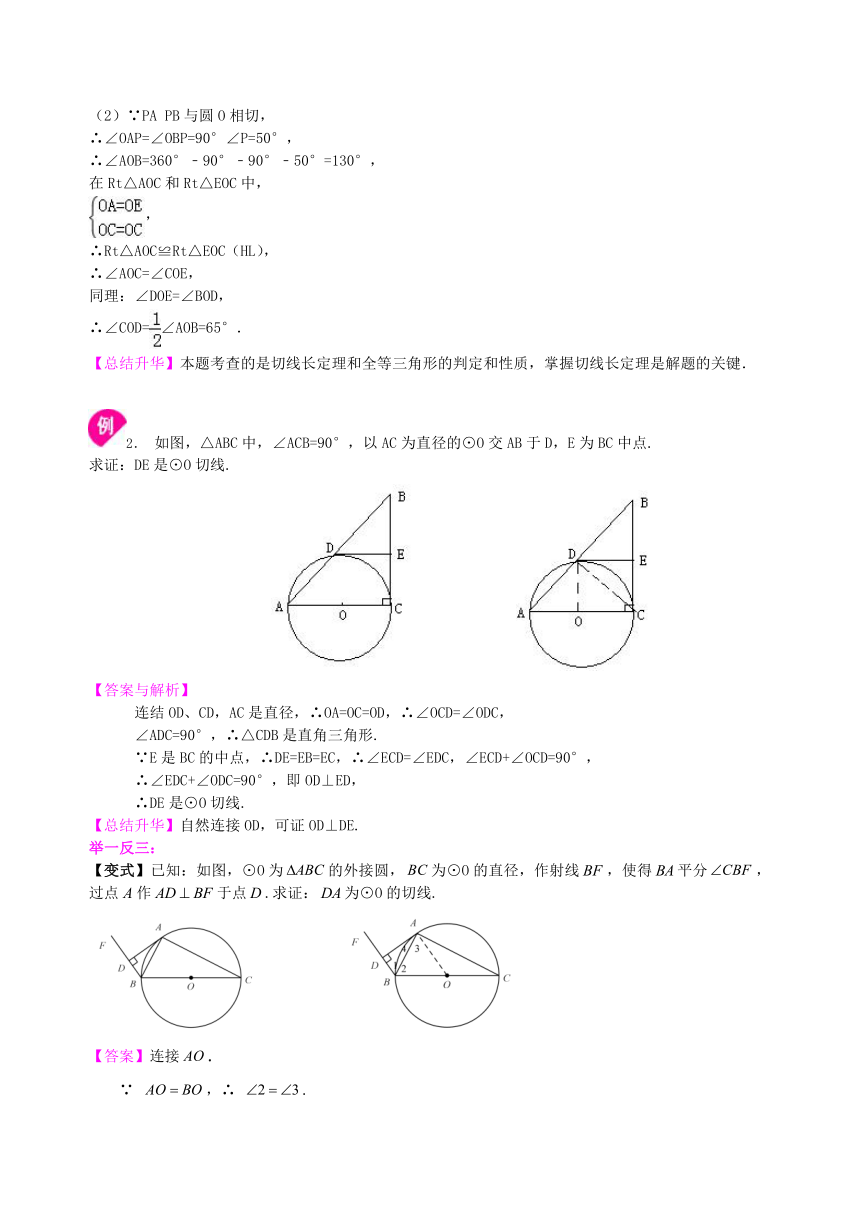
2. 如图,△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,E为BC中点.
求证:DE是⊙O切线.
【答案与解析】
连结OD、CD,AC是直径,∴OA=OC=OD,∴∠OCD=∠ODC,
∠ADC=90°,∴△CDB是直角三角形.
∵E是BC的中点,∴DE=EB=EC,∴∠ECD=∠EDC,∠ECD+∠OCD=90°,
∴∠EDC+∠ODC=90°,即OD⊥ED,
∴DE是⊙O切线.
【总结升华】自然连接OD,可证OD⊥DE.
举一反三:
【变式】已知:如图,⊙O为的外接圆,为⊙O的直径,作射线,使得平分,过点作于点.求证:为⊙O的切线.
【答案】连接.
∵ ,∴ .
∵ ,∴ . ∴ .
∴ ∥.
∵ ,∴ .∴ .
∵ 是⊙O半径,∴ 为⊙O的切线.
3.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
【答案】D;
【解析】
∵AE与圆O切于点F,
显然根据切线长定理有AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4﹣x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4﹣x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4﹣1=3cm,
∴S△ADE=AD?DE÷2=3×4÷2=6cm2.
【总结升华】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF,EF=EC.
类型二、圆外切四边形
4.(2019?西青区二模)已知四边形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(Ⅰ)如图1,求∠AOD的度数;
(Ⅱ)如图1,若AO=8cm,DO=6cm,求AD、OE的长;
(Ⅲ)如图2,若F是AD的中点,在(Ⅱ)中条件下,求FO的长.
【答案与解析】解:(Ⅰ)∵⊙O为四边形ABCD的内切圆,
∴AD、AB、CD为⊙O的切线,
∴OD平分∠ADC,OA平分∠BAD,
即∠ODA=∠ADC,∠OAD=∠BAC,
∵AB∥CD,
∴∠ADC+∠BAC=180°,
∴∠ODA+∠OAD=90°,
∴∠AOD=90°;
(Ⅱ)在Rt△AOD中,∵AO=8cm,DO=6cm,
∴AD==10(cm),
∵AD切⊙O于E,
∴OE⊥AD,
∴OE?AD=OD?OA,
∴OE==(cm);
(Ⅲ)∵F是AD的中点,
∴FO=AD=×10=5(cm).
【总结升华】本题考查了三角形的内切圆与内心,也考查了切线长定理.
举一反三:
【变式】在圆外切四边形ABCD中,AB:BC:CD:AD只可能是( ).
A.2:3:4:5 B.3:4:6:5 C.5:4:1:3 D.3:4:2:5
【答案】B.
切线长定理—巩固练习(基础)
【巩固练习】
一、选择题 1. 下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A.(a+b+c)r B.2(a+b+c) C.(a+b+c)r D.(a+b+c)r
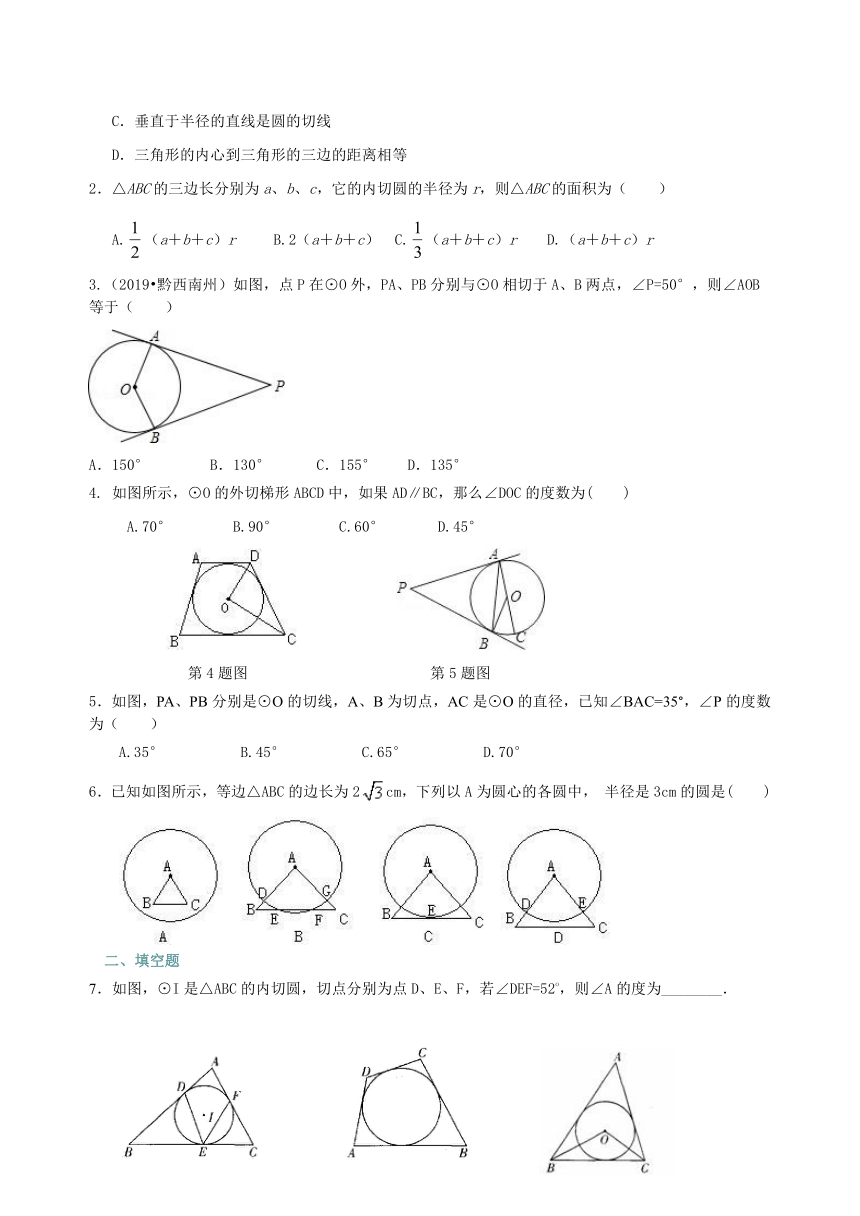
3.(2019?黔西南州)如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
A.150° B.130° C.155° D.135°
4. 如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( ) A.70° B.90° C.60° D.45° 第4题图 第5题图
5.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45° C.65° D.70°
6.已知如图所示,等边△ABC的边长为2cm,下列以A为圆心的各圆中, 半径是3cm的圆是( )
二、填空题
7.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.
第7题图 第8题图 第9题图
8.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
9.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
10.如图,、分别切⊙于点、,点是⊙上一点,且,则____度.
第10题图 第11题图
11.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
12.(2019?鄂州)已知点P是半径为1的⊙O外一点,PA切⊙O于点A,且PA=1,AB是⊙O的弦,AB=,连接PB,则PB= .
三、解答题
13.已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
14. 已知:如图,PA,PB,DC分别切⊙O于A,B,E点.
(1)若∠P=40°,求∠COD;
(2)若PA=10cm,求△PCD的周长.
15.(2019?南丹县一模)如图,∠C=90°,⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,连接OE,OF.AO的延长线交BC于点D,AC=6,CD=2.
(1)求证:四边形OECF为正方形;
(2)求⊙O的半径;
(3)求AB的长.
【答案与解析】
一、选择题 1.【答案】C.
【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线.
2.【答案】A.
【解析】连结内心与三个顶点,则△ABC的面积等于三个三角形的面积之和,所以△ABC的面积
为a·r+b·r+c·r=(a+b+c)r.
3.【答案】B;
【解析】∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故选B.
4.【答案】B;
【解析】由AD∥BC,得∠ADC+∠BCD=180°,又AD、DC、BC与⊙O相切,
所以∠ODC=∠ADC,∠OCD=∠BCD,所以∠ODC+∠OCD=×180°=90°,所以∠DOC=90°.
故选B.
5.【答案】D;
【解析】根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.
6.【答案】C;
【解析】易求等边△ABC的高为3cm等于圆的半径,所以圆A与BC相切,故选C.
二、填空题
7.【答案】76°;
【解析】连接ID,IF ∵∠DEF=52°, ∴∠DIF=104°,
∵D、F是切点, ∴DI⊥AB,IF⊥AC ,
∴∠ADI=∠AFI=90°, ∴∠A=1800-1040=76°.
8.【答案】52;
【解析】提示:AB+CD=AD+BC.
9.【答案】115°;
【解析】∵∠A=500 ∴∠ABC+∠ACB=130°,
∵OB,OC分别平分∠ABC,∠ACB, ∴∠OBC+∠OCB=65°,
∴∠BOC=1800-650=115°.
10.【答案】60°;
【解析】连结OA、OB,则∠AOB=120°,在四边形OAPB中,∠P=360°-90°-90°-120°=60°.
11.【答案】26°;
【解析】连结OA,则∠AOC=64°,∠P=90°-64°=26°.
12.【答案】1或.
【解析】连接OA,
(1)如图1,连接OA,
∵PA=AO=1,OA=OB,PA是⊙的切线,
∴∠AOP=45°∵OA=OB,
∴∠BOP=∠AOP=45°,
在△POA与△POB中,,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,连接OA,与PB交于C,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=,1
∴OP=;
∵AB=,
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=,
∴BC=,
∴PB=.
故答案为:1或.
三、解答题
13.【答案与解析】
解:∵AB,AC分别与⊙O相切,
∴OB⊥AB,
∵AO=d,BO=r,
∴AB==,
∵MN切圆O于点P,
∴MP=MB,NP=NC,
∴△AMN的周长=AM+AN+MN=AM+PM+PN+AN=AM+BM+AN+PN=AB+AC=2AB=2,
∴△AMN的周长是一个定值,这个定值为2.
14. 【答案与解析】
(1)∵PA,PB,DC分别切圆O于A,B,E点
∴OC与OD就是△PCD的两个外角的平分线
∴∠COD=90°- ∠P=90°-20°=70°
(2)∵PA与PB分别切⊙O于A、B两点,CD切⊙O于E, ∴PA=PA=10cm,CA=CE,DE=DB, ∴△PCD的周长=PD+DE+EC+PC=PD+DB+CA+PC=PA+PB=20cm.故答案为20 cm.
15. 【答案与解析】
(1)证明:∵⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,
∴∠C=∠CFO=∠CEO=90°,
∴四边形CFOE是矩形,
∵OF=OE,
∴四边形OECF为正方形;
(2)解:由题意可得:EO∥AC,
∴△DEO∽△DCA,
∴=,
设⊙O的半径为x,
则=,
解得:x=1.5,
故⊙O的半径为1.5;
(3)解:∵⊙O的半径为1.5,AC=6,
∴CF=1.5,AF=4.5
∴AG=4.5,
设BG=BE=y,
∴在Rt△ACB中
AC2+BC2=AB2,
∴62+(y+1.5)2=(4.5+y)2,
解得:y=3,
∴AB=AG+BG=4.5+3=7.5.
【学习目标】
1.了解切线长定义,掌握切线长定理;
2.了解圆外切四边形定义及性质;
3. 利用切线长定理解决相关的计算和证明.
【要点梳理】
要点一、切线长定理 1.切线长: 经过圆外一点作圆的切线,这点和切点之间的线段的长,叫做这点到圆的切线长. 要点诠释: 切线长是指圆外一点和切点之间的线段的长,不是“切线的长”的简称.切线是直线,而非线段. 2.切线长定理: 从圆外一点可以引圆的两条切线,它们的切线长相等,这一点和圆心的连线平分两条切线的夹角. 要点诠释: 切线长定理包含两个结论:线段相等和角相等.
要点二、圆外切四边形的性质
1.圆外切四边形
四边形的四条边都与同一个圆相切,那这个四边形叫做圆的外切四边形.
2.圆外切四边形性质
圆外切四边形的两组对边之和相等. 【典型例题】
类型一、切线长定理
1.(2019秋?湛江校级月考)已知PA、PB分别切⊙O于A、B,E为劣弧AB上一点,过E点的切线交PA于C、交PB于D.
(1)若PA=6,求△PCD的周长.
(2)若∠P=50°求∠DOC.
【答案与解析】
解:(1)连接OE,
∵PA、PB与圆O相切,
∴PA=PB=6,
同理可得:AC=CE,BD=DE,
△PCD的周长=PC+PD+CD=PC+PD+CE+DE=PA+PB=12;
(2)∵PA PB与圆O相切,
∴∠OAP=∠OBP=90°∠P=50°,
∴∠AOB=360°﹣90°﹣90°﹣50°=130°,
在Rt△AOC和Rt△EOC中,
,
∴Rt△AOC≌Rt△EOC(HL),
∴∠AOC=∠COE,
同理:∠DOE=∠BOD,
∴∠COD=∠AOB=65°.
【总结升华】本题考查的是切线长定理和全等三角形的判定和性质,掌握切线长定理是解题的关键.
2. 如图,△ABC中,∠ACB=90°,以AC为直径的⊙O交AB于D,E为BC中点.
求证:DE是⊙O切线.
【答案与解析】
连结OD、CD,AC是直径,∴OA=OC=OD,∴∠OCD=∠ODC,
∠ADC=90°,∴△CDB是直角三角形.
∵E是BC的中点,∴DE=EB=EC,∴∠ECD=∠EDC,∠ECD+∠OCD=90°,
∴∠EDC+∠ODC=90°,即OD⊥ED,
∴DE是⊙O切线.
【总结升华】自然连接OD,可证OD⊥DE.
举一反三:
【变式】已知:如图,⊙O为的外接圆,为⊙O的直径,作射线,使得平分,过点作于点.求证:为⊙O的切线.
【答案】连接.
∵ ,∴ .
∵ ,∴ . ∴ .
∴ ∥.
∵ ,∴ .∴ .
∵ 是⊙O半径,∴ 为⊙O的切线.
3.如图,正方形ABCD边长为4cm,以正方形的一边BC为直径在正方形ABCD内作半圆,过A作半圆的切线,与半圆相切于F点,与DC相交于E点,则△ADE的面积( )
A.12 B.24 C.8 D.6
【答案】D;
【解析】
∵AE与圆O切于点F,
显然根据切线长定理有AF=AB=4cm,EF=EC,
设EF=EC=xcm,
则DE=(4﹣x)cm,AE=(4+x)cm,
在三角形ADE中由勾股定理得:
(4﹣x)2+42=(4+x)2,
∴x=1cm,
∴CE=1cm,
∴DE=4﹣1=3cm,
∴S△ADE=AD?DE÷2=3×4÷2=6cm2.
【总结升华】此题主要考查圆的切线长定理,正方形的性质和勾股定理等知识,解答本题关键是运用切线长定理得出AB=AF,EF=EC.
类型二、圆外切四边形
4.(2019?西青区二模)已知四边形ABCD中,AB∥CD,⊙O为内切圆,E为切点.
(Ⅰ)如图1,求∠AOD的度数;
(Ⅱ)如图1,若AO=8cm,DO=6cm,求AD、OE的长;
(Ⅲ)如图2,若F是AD的中点,在(Ⅱ)中条件下,求FO的长.
【答案与解析】解:(Ⅰ)∵⊙O为四边形ABCD的内切圆,
∴AD、AB、CD为⊙O的切线,
∴OD平分∠ADC,OA平分∠BAD,
即∠ODA=∠ADC,∠OAD=∠BAC,
∵AB∥CD,
∴∠ADC+∠BAC=180°,
∴∠ODA+∠OAD=90°,
∴∠AOD=90°;
(Ⅱ)在Rt△AOD中,∵AO=8cm,DO=6cm,
∴AD==10(cm),
∵AD切⊙O于E,
∴OE⊥AD,
∴OE?AD=OD?OA,
∴OE==(cm);
(Ⅲ)∵F是AD的中点,
∴FO=AD=×10=5(cm).
【总结升华】本题考查了三角形的内切圆与内心,也考查了切线长定理.
举一反三:
【变式】在圆外切四边形ABCD中,AB:BC:CD:AD只可能是( ).
A.2:3:4:5 B.3:4:6:5 C.5:4:1:3 D.3:4:2:5
【答案】B.
切线长定理—巩固练习(基础)
【巩固练习】
一、选择题 1. 下列说法中,不正确的是 ( )
A.三角形的内心是三角形三条内角平分线的交点
B.锐角三角形、直角三角形、钝角三角形的内心都在三角形内部
C.垂直于半径的直线是圆的切线
D.三角形的内心到三角形的三边的距离相等
2.△ABC的三边长分别为a、b、c,它的内切圆的半径为r,则△ABC的面积为( )
A.(a+b+c)r B.2(a+b+c) C.(a+b+c)r D.(a+b+c)r
3.(2019?黔西南州)如图,点P在⊙O外,PA、PB分别与⊙O相切于A、B两点,∠P=50°,则∠AOB等于( )
A.150° B.130° C.155° D.135°
4. 如图所示,⊙O的外切梯形ABCD中,如果AD∥BC,那么∠DOC的度数为( ) A.70° B.90° C.60° D.45° 第4题图 第5题图
5.如图,PA、PB分别是⊙O的切线,A、B为切点,AC是⊙O的直径,已知∠BAC=35°,∠P的度数为( )
A.35° B.45° C.65° D.70°
6.已知如图所示,等边△ABC的边长为2cm,下列以A为圆心的各圆中, 半径是3cm的圆是( )
二、填空题
7.如图,⊙I是△ABC的内切圆,切点分别为点D、E、F,若∠DEF=52o,则∠A的度为________.
第7题图 第8题图 第9题图
8.如图,一圆内切于四边形ABCD,且AB=16,CD=10,则四边形ABCD的周长为________.
9.如图,已知⊙O是△ABC的内切圆,∠BAC=50o,则∠BOC为____________度.
10.如图,、分别切⊙于点、,点是⊙上一点,且,则____度.
第10题图 第11题图
11.如图,PA与⊙O相切,切点为A,PO交⊙O于点C,点B是优弧CBA上一点,若∠ABC=32°,则∠P的度数为 .
12.(2019?鄂州)已知点P是半径为1的⊙O外一点,PA切⊙O于点A,且PA=1,AB是⊙O的弦,AB=,连接PB,则PB= .
三、解答题
13.已知,如图,A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,P是BC上任意一点,过点P作⊙O的切线,交AB于点M,交AC于点N,设AO=d,BO=r.求证:△AMN的周长是一个定值,并求出这个定值.
14. 已知:如图,PA,PB,DC分别切⊙O于A,B,E点.
(1)若∠P=40°,求∠COD;
(2)若PA=10cm,求△PCD的周长.
15.(2019?南丹县一模)如图,∠C=90°,⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,连接OE,OF.AO的延长线交BC于点D,AC=6,CD=2.
(1)求证:四边形OECF为正方形;
(2)求⊙O的半径;
(3)求AB的长.
【答案与解析】
一、选择题 1.【答案】C.
【解析】经过半径的外端,并且垂直于这条半径的直线是圆的切线.
2.【答案】A.
【解析】连结内心与三个顶点,则△ABC的面积等于三个三角形的面积之和,所以△ABC的面积
为a·r+b·r+c·r=(a+b+c)r.
3.【答案】B;
【解析】∵PA、PB是⊙O的切线,
∴PA⊥OA,PB⊥OB,
∴∠PAO=∠PBO=90°,
∵∠P=50°,
∴∠AOB=130°.
故选B.
4.【答案】B;
【解析】由AD∥BC,得∠ADC+∠BCD=180°,又AD、DC、BC与⊙O相切,
所以∠ODC=∠ADC,∠OCD=∠BCD,所以∠ODC+∠OCD=×180°=90°,所以∠DOC=90°.
故选B.
5.【答案】D;
【解析】根据切线的性质定理得∠PAC=90°,∴∠PAB=90°﹣∠BAC=90°﹣35°=55°.根据切线长定理得PA=PB,所以∠PBA=∠PAB=55°,所以∠P=70°.
6.【答案】C;
【解析】易求等边△ABC的高为3cm等于圆的半径,所以圆A与BC相切,故选C.
二、填空题
7.【答案】76°;
【解析】连接ID,IF ∵∠DEF=52°, ∴∠DIF=104°,
∵D、F是切点, ∴DI⊥AB,IF⊥AC ,
∴∠ADI=∠AFI=90°, ∴∠A=1800-1040=76°.
8.【答案】52;
【解析】提示:AB+CD=AD+BC.
9.【答案】115°;
【解析】∵∠A=500 ∴∠ABC+∠ACB=130°,
∵OB,OC分别平分∠ABC,∠ACB, ∴∠OBC+∠OCB=65°,
∴∠BOC=1800-650=115°.
10.【答案】60°;
【解析】连结OA、OB,则∠AOB=120°,在四边形OAPB中,∠P=360°-90°-90°-120°=60°.
11.【答案】26°;
【解析】连结OA,则∠AOC=64°,∠P=90°-64°=26°.
12.【答案】1或.
【解析】连接OA,
(1)如图1,连接OA,
∵PA=AO=1,OA=OB,PA是⊙的切线,
∴∠AOP=45°∵OA=OB,
∴∠BOP=∠AOP=45°,
在△POA与△POB中,,
∴△POA≌△POB,
∴PB=PA=1;
(2)如图2,连接OA,与PB交于C,
∵PA是⊙O的切线,
∴OA⊥PA,
而PA=AO=,1
∴OP=;
∵AB=,
而OA=OB=1,
∴AO⊥BO,
∴四边形PABO是平行四边形,
∴PB,AO互相平分;
设AO交PB与点C,
即OC=,
∴BC=,
∴PB=.
故答案为:1或.
三、解答题
13.【答案与解析】
解:∵AB,AC分别与⊙O相切,
∴OB⊥AB,
∵AO=d,BO=r,
∴AB==,
∵MN切圆O于点P,
∴MP=MB,NP=NC,
∴△AMN的周长=AM+AN+MN=AM+PM+PN+AN=AM+BM+AN+PN=AB+AC=2AB=2,
∴△AMN的周长是一个定值,这个定值为2.
14. 【答案与解析】
(1)∵PA,PB,DC分别切圆O于A,B,E点
∴OC与OD就是△PCD的两个外角的平分线
∴∠COD=90°- ∠P=90°-20°=70°
(2)∵PA与PB分别切⊙O于A、B两点,CD切⊙O于E, ∴PA=PA=10cm,CA=CE,DE=DB, ∴△PCD的周长=PD+DE+EC+PC=PD+DB+CA+PC=PA+PB=20cm.故答案为20 cm.
15. 【答案与解析】
(1)证明:∵⊙O是Rt△ABC的内切圆,分别切BC,AC,AB于点E,F,G,
∴∠C=∠CFO=∠CEO=90°,
∴四边形CFOE是矩形,
∵OF=OE,
∴四边形OECF为正方形;
(2)解:由题意可得:EO∥AC,
∴△DEO∽△DCA,
∴=,
设⊙O的半径为x,
则=,
解得:x=1.5,
故⊙O的半径为1.5;
(3)解:∵⊙O的半径为1.5,AC=6,
∴CF=1.5,AF=4.5
∴AG=4.5,
设BG=BE=y,
∴在Rt△ACB中
AC2+BC2=AB2,
∴62+(y+1.5)2=(4.5+y)2,
解得:y=3,
∴AB=AG+BG=4.5+3=7.5.
