青岛版七年级数学下册12.1 平方差公式课件(共16张PPT)
文档属性
| 名称 | 青岛版七年级数学下册12.1 平方差公式课件(共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 827.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 19:53:14 | ||
图片预览





文档简介
(共16张PPT)
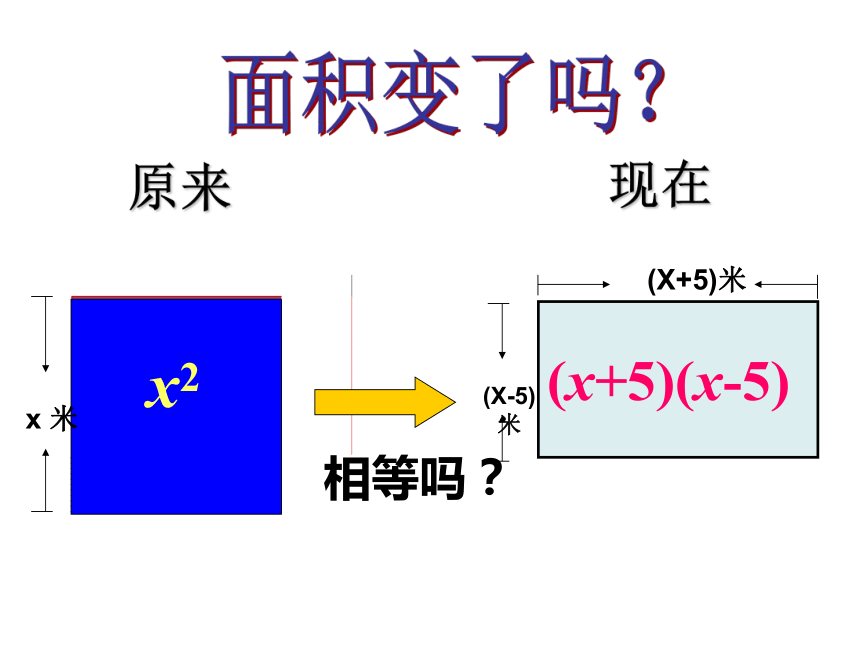
有一个狡猾的庄园主,把一边长为x米的正方形土地租给王大爷种植.有一年他对王大爷说:“我把这块地的一边增加5米,另一边减少5米,继续租给你,你也没吃亏,你看如何?”王大爷一听觉得没有吃亏,就答应了.回到家中,就把这件事对邻居讲了,邻居一听,说:“王大爷您吃亏了!”王大爷非常吃惊,同学们,你能告诉王大爷这是为什么吗?
x2
(x+5)(x-5)
相等吗?
原来
现在
借助几何图形和多项式乘法法则,探索平方差公式,说出公式的结构特征,并能用公式简化计算过程。
a
b
a+b
a-b
平方差公式的几何背景
平方差公式的代数推导
请利用多项式的乘法,计算下面各题。
①(a+2)(a-2)=
② (x+2y)(x-2y)=
③ (a+b)(a-b)=
a2-2a+2a-22
=a2-22
(a+b)(a-b)
(多项式乘法法则)
(合并同类项)
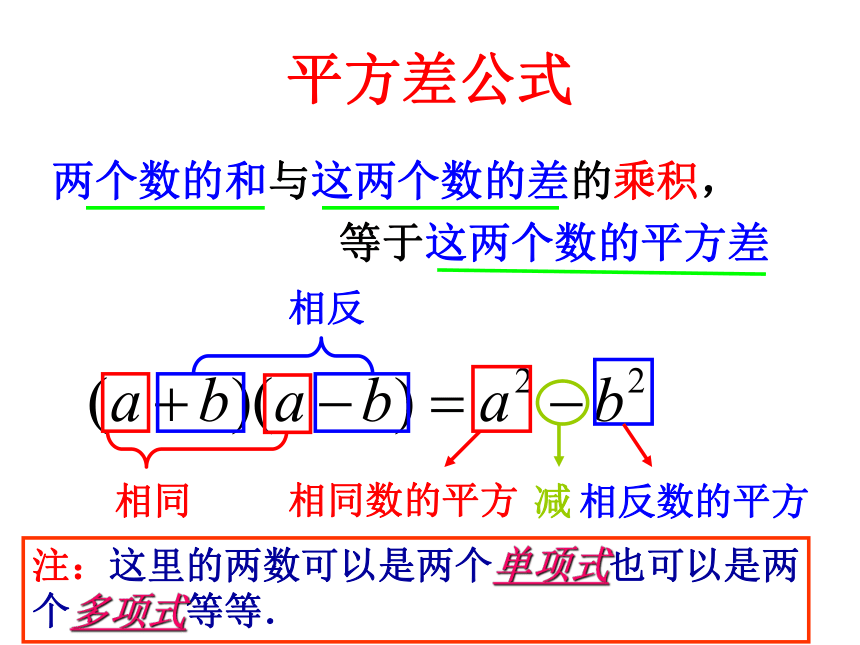
平方差公式
两个数的和与这两个数的差的乘积,
等于这两个数的平方差
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1+x)(1-x)
(-3+a)(-3-a)
(x-y)(-y-x)
(1+a)(-1+a)
a
b
1
x
-3
a
a
1
-y
x
(a-b)(a+b)
平方差要判断,分清a、b是关键,相同的是a,相反的是b,
a的平方减去b的平方,把结果算!
(6) (3y ? x)(? x ? 3y)
( )
( )
( )
( )
( )
( )
(1) ( 2x-3)(-2x+3)
(2) (2+3a2)(3a2-2)
(3)
(4) (-5-2x)(2x+5)
(5) (?2x+y)(y?2x).
2.
公式的应用
例、用平方差公式计算
解:原式
基础探索
例1.利用平方差公式计算。
(1)
(2)
(3)
(4)
例、下列计算对不对?如果不对,怎样改正?
错
错
3)
错
能力养成
例2.平方差公式的妙用。
(1)
(2)
1992×2008
20172–20162
畅谈收获
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
2) 右边是这两个数的平方差.
1) 左边是两个数的和与这两个数的差的积.
注:这里的两数可以是两个单项式也可以是两个多项式等等.
利用平方差公式计算:
解:原式=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
(2+1)(22+1)(24+1)(28+1)+1
一路下来,我们学习了很多知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
有一个狡猾的庄园主,把一边长为x米的正方形土地租给王大爷种植.有一年他对王大爷说:“我把这块地的一边增加5米,另一边减少5米,继续租给你,你也没吃亏,你看如何?”王大爷一听觉得没有吃亏,就答应了.回到家中,就把这件事对邻居讲了,邻居一听,说:“王大爷您吃亏了!”王大爷非常吃惊,同学们,你能告诉王大爷这是为什么吗?
x2
(x+5)(x-5)
相等吗?
原来
现在
借助几何图形和多项式乘法法则,探索平方差公式,说出公式的结构特征,并能用公式简化计算过程。
a
b
a+b
a-b
平方差公式的几何背景
平方差公式的代数推导
请利用多项式的乘法,计算下面各题。
①(a+2)(a-2)=
② (x+2y)(x-2y)=
③ (a+b)(a-b)=
a2-2a+2a-22
=a2-22
(a+b)(a-b)
(多项式乘法法则)
(合并同类项)
平方差公式
两个数的和与这两个数的差的乘积,
等于这两个数的平方差
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1+x)(1-x)
(-3+a)(-3-a)
(x-y)(-y-x)
(1+a)(-1+a)
a
b
1
x
-3
a
a
1
-y
x
(a-b)(a+b)
平方差要判断,分清a、b是关键,相同的是a,相反的是b,
a的平方减去b的平方,把结果算!
(6) (3y ? x)(? x ? 3y)
( )
( )
( )
( )
( )
( )
(1) ( 2x-3)(-2x+3)
(2) (2+3a2)(3a2-2)
(3)
(4) (-5-2x)(2x+5)
(5) (?2x+y)(y?2x).
2.
公式的应用
例、用平方差公式计算
解:原式
基础探索
例1.利用平方差公式计算。
(1)
(2)
(3)
(4)
例、下列计算对不对?如果不对,怎样改正?
错
错
3)
错
能力养成
例2.平方差公式的妙用。
(1)
(2)
1992×2008
20172–20162
畅谈收获
1、平方差公式是特殊的多项式乘法,要理解并掌握公式的结构特征.
2) 右边是这两个数的平方差.
1) 左边是两个数的和与这两个数的差的积.
注:这里的两数可以是两个单项式也可以是两个多项式等等.
利用平方差公式计算:
解:原式=(2-1)(2+1)(22+1)(24+1)(28+1)+1
=(22-1)(22+1)(24+1)(28+1)+1
(2+1)(22+1)(24+1)(28+1)+1
一路下来,我们学习了很多知识,也有了很多的新想法。你能谈谈自己的收获吗?说一说,让大家一起来分享。
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
