青岛版七年级数学下册第12章 乘法公式与因式分解12.1平方差公式课件(共21张)
文档属性
| 名称 | 青岛版七年级数学下册第12章 乘法公式与因式分解12.1平方差公式课件(共21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-21 12:16:58 | ||
图片预览








文档简介
(共21张PPT)
授课教师:刘亚青
成武县智楼学区智楼中学
美丽的广场,是人们休闲的好地方.
某广场呈长方形,长为803米,宽为797米.它的面积是多少?
回忆:多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
多项式乘多项式法则:多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加。
某中学计划将一个边长为a 米
的正方形花坛进行改造,
(1)改造成长为( a+2 )米,宽为(a-2)
米的长方形,新花坛的面积是多少?
(2)改造成长为( a+1 )米,宽为(a-1)
米的长方形呢?
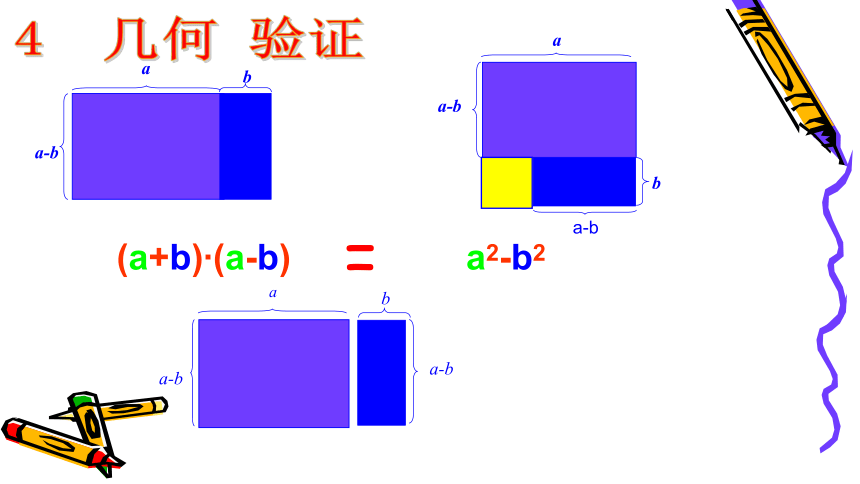
(a + b)( a-b) = ?
(a + b)( a-b)
-b2
=a2
-b2
=a2
-a·b
+a·b
(a+b)?(a-b)
a2-b2
=
平方差公式:
(a+b)(a?b)=
a2?b2
两个数的和与这两个数的差的乘积,
等于
这两数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
(a+b)(a-b)=(a)2-(b)2
适当交换
合理加括号
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1+x)(1-x)
(-3+a)(-3-a)
(x-y)(-y-x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
-y
x
( -y)2-x2
(a-b)(a+b)
平方差要判断,分清a、b是关键,相同的是a,相反的是b,
a的平方减去b的平方,把结果算!
(1)(x+5)(-x-5)
(3)(x2+y ) (x2 –y)
(2)(m+n)(-m+n)
(4)(3X- y) (-3x-y)
(5) (-5x-4y)(-5x+4y)
(6)(7a-2b)(-7a+2b)
2. 请帮下列各式找到自己的家。
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
(1)(3x+2y)(3x-2y)
解:原式= (3x)2 - (2y)2
=9x2 - 4y2
简化多项式的乘法运算
(2 )(-7+2m2)(-7-2m2).
解:原式=(-7)2-(2m2)2
= 49-4m4
(3)
(x-1) ?(x+1) ?(x2 + 1)
解: (x-1) ?(x+1) ?(x2+ 1)
=(x2-1) ?(x2+1)
=x4-1
用平方差公式计算:
(1)
(2)
=25a2-4
=4x2-64
例2 利用平方差公式计算本章“情境导航”中提出的问题 .
803×797
解: 803×797
= 8002-32
=640 000 – 9
=(800+3)(800-3)
=639 991
提供有理数乘法的速算方法
某广场呈长方形,长
为803米,宽为797米.
它的面积是多少?
所以,这个广场的面积是639991平方米.
(2)2014×2016 -20152
= - 1
=9 996
(1)98×102
用平方差公式计算:
用平方差公式计算:
(3+2)×(32+22)×(34+24)×(38+28)×(316+216)
(1)简化某些多项式的乘法运算
(2)提供某些有理数乘法的速算方法
a2-b2
(a+b)(a-b)
=
平方差公式
首先要辨认准确
哪个是 a?(相同项)
哪个是 b?(相反项).
习题12.1 1 ,2, 5
挑战自我
授课教师:刘亚青
成武县智楼学区智楼中学
美丽的广场,是人们休闲的好地方.
某广场呈长方形,长为803米,宽为797米.它的面积是多少?
回忆:多项式与多项式是如何相乘的?
(a+b)(m+n)
=am
+an
+bm
+bn
多项式乘多项式法则:多项式与多项式相乘,先用一个多项式的每一项分别乘另一个多项式的每一项,再把所得的积相加。
某中学计划将一个边长为a 米
的正方形花坛进行改造,
(1)改造成长为( a+2 )米,宽为(a-2)
米的长方形,新花坛的面积是多少?
(2)改造成长为( a+1 )米,宽为(a-1)
米的长方形呢?
(a + b)( a-b) = ?
(a + b)( a-b)
-b2
=a2
-b2
=a2
-a·b
+a·b
(a+b)?(a-b)
a2-b2
=
平方差公式:
(a+b)(a?b)=
a2?b2
两个数的和与这两个数的差的乘积,
等于
这两数的平方差.
公式变形:
1、(a – b ) ( a + b) = a2 - b2
2、(b + a )( -b + a ) = a2 - b2
(a+b)(a-b)=(a)2-(b)2
适当交换
合理加括号
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等等.
(1+x)(1-x)
(-3+a)(-3-a)
(x-y)(-y-x)
(1+a)(-1+a)
1、找一找、填一填
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
-y
x
( -y)2-x2
(a-b)(a+b)
平方差要判断,分清a、b是关键,相同的是a,相反的是b,
a的平方减去b的平方,把结果算!
(1)(x+5)(-x-5)
(3)(x2+y ) (x2 –y)
(2)(m+n)(-m+n)
(4)(3X- y) (-3x-y)
(5) (-5x-4y)(-5x+4y)
(6)(7a-2b)(-7a+2b)
2. 请帮下列各式找到自己的家。
(a + b ) ( a – b ) = a2 - b2
例1、用平方差公式计算
(1)(3x+2y)(3x-2y)
解:原式= (3x)2 - (2y)2
=9x2 - 4y2
简化多项式的乘法运算
(2 )(-7+2m2)(-7-2m2).
解:原式=(-7)2-(2m2)2
= 49-4m4
(3)
(x-1) ?(x+1) ?(x2 + 1)
解: (x-1) ?(x+1) ?(x2+ 1)
=(x2-1) ?(x2+1)
=x4-1
用平方差公式计算:
(1)
(2)
=25a2-4
=4x2-64
例2 利用平方差公式计算本章“情境导航”中提出的问题 .
803×797
解: 803×797
= 8002-32
=640 000 – 9
=(800+3)(800-3)
=639 991
提供有理数乘法的速算方法
某广场呈长方形,长
为803米,宽为797米.
它的面积是多少?
所以,这个广场的面积是639991平方米.
(2)2014×2016 -20152
= - 1
=9 996
(1)98×102
用平方差公式计算:
用平方差公式计算:
(3+2)×(32+22)×(34+24)×(38+28)×(316+216)
(1)简化某些多项式的乘法运算
(2)提供某些有理数乘法的速算方法
a2-b2
(a+b)(a-b)
=
平方差公式
首先要辨认准确
哪个是 a?(相同项)
哪个是 b?(相反项).
习题12.1 1 ,2, 5
挑战自我
同课章节目录
- 第8章 角
- 8.1 角的表示
- 8.2 角的比较
- 8.3 角的度量
- 8.4 对顶角
- 8.5 垂直
- 第9章 平行线
- 9.1 同位角、内错角、同旁内角
- 9.2 平行线和它的画法
- 9.3 平行线的性质
- 9.4 平行线的判定
- 第10章 一次方程组
- 10.1 认识二元一次方程组
- 10.2 二元一次方程组的解法
- 10.3 三元一次方程组
- 10.4 列方程组解应用题
- 第11章 整式的乘除
- 11.1 同底数幂的乘法
- 11.2 积的乘方与幂的乘方
- 11.3 单项式的乘法
- 11.4 多项式乘多项式
- 11.5 同底数幂的除法
- 11.6 零指数幂与负整数指数幂
- 第12章 乘法公式与因式分解
- 12.1 平方差公式
- 12.2 完全平方公式
- 12.3 用提公因式法进行因式分解
- 12.4 用公式法进行因式分解
- 第13章 平面图形的认识
- 13.1 三角形
- 13.2 多边形
- 13.3 圆
- 第14章 位置与坐标
- 14.1 用有序数对表示位置
- 14.2 平面直角坐标系
- 14.3 直角坐标系中的图形
- 14.4 用方向和距离描述两个物体的相对位置
