北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第5讲 二次函数y=ax^2(a≠0)的图象与性质(提高)含答案
文档属性
| 名称 | 北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第5讲 二次函数y=ax^2(a≠0)的图象与性质(提高)含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 355.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 12:56:22 | ||
图片预览


文档简介
二次函数y=ax2(a≠0)的图象与性质—知识讲解(提高)
【学习目标】
1.经历探索二次函数y=ax2和y=ax2+c的图象的作法和性质的过程,进一步获得将表格、表达式、图象三者联系起来的经验.
2.会作出y=ax2和y=ax2+c的图象,并能比较它们与y=x2的异同,理解a与c对二次函数图象的影响.
3.能说出y=ax2+c与y=ax2图象的开口方向、对称轴和顶点坐标.
4.体会二次函数是某些实际问题的数学模型.
5.掌握二次函数y=ax2(a≠0)与y=ax2+c (a≠0)的图象之间的关系.
【要点梳理】
要点一、二次函数y=ax2(a≠0)的图象与性质
1.二次函数y=ax2(a≠0)的图象
二次函数y=ax2的图象(如图),是一条关于y轴对称的曲线,这样的曲线叫做抛物线.
抛物线y=ax2(a≠0)的对称轴是y轴,它的顶点是坐标原点.当a> 0时,抛物线的开口向上,顶点是它的最低点;当a<0时,抛物线的开口向下,顶点是它的最高点.
2.二次函数y=ax2(a≠0)的图象的画法——描点法
描点法画图的基本步骤:列表、描点、连线.
(1)列表:选择自变量取值范围内的一些适当的x的值,求出相应的y值,填入表中.(自变量x的值写在第一行,其值从左到右,从小到大.)
(2)描点:以表中每对x和y的值为坐标,在坐标平面内准确描出相应的点.一般地,点取的越多,图象就越准确.
(3)连线:按照自变量的值由小到大的顺序,把所描的点用平滑的曲线连结起来.
要点诠释:
(1)用描点法画二次函数y=ax2(a≠0)的图象时,应在顶点的左、右两侧对称地选取自变量x的值,然后计算出对应的y值.
(2)二次函数y=ax2(a≠0)的图象,是轴对称图形,对称轴是y轴.y=ax2(a≠0)是最简单的二次函数.
(3)画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
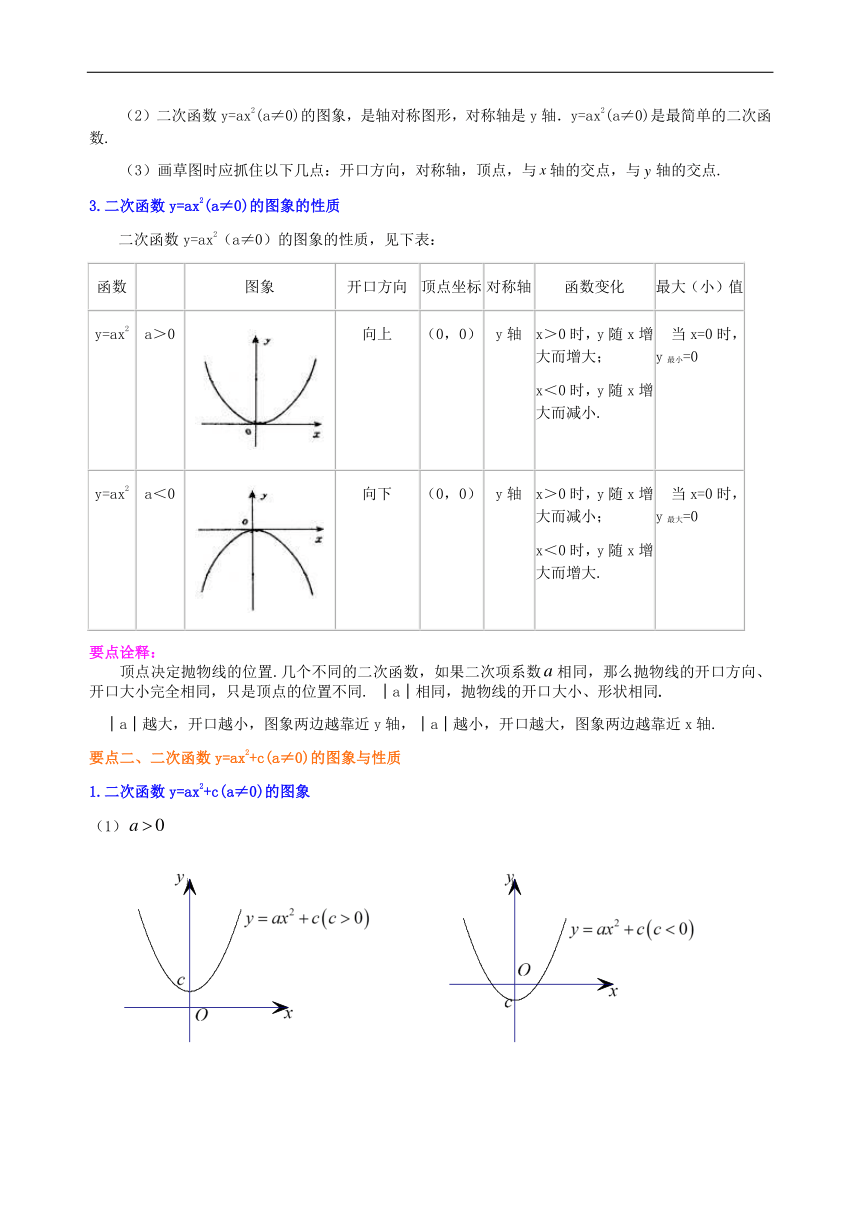
3.二次函数y=ax2(a≠0)的图象的性质
二次函数y=ax2(a≠0)的图象的性质,见下表:
函数
图象
开口方向
顶点坐标
对称轴
函数变化
最大(小)值
y=ax2
a>0
向上
(0,0)
y轴
x>0时,y随x增大而增大;
x<0时,y随x增大而减小.
当x=0时,y最小=0
y=ax2
a<0
向下
(0,0)
y轴
x>0时,y随x增大而减小;
x<0时,y随x增大而增大.
当x=0时,y最大=0
要点诠释: 顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. │a│相同,抛物线的开口大小、形状相同.
│a│越大,开口越小,图象两边越靠近y轴,│a│越小,开口越大,图象两边越靠近x轴.
要点二、二次函数y=ax2+c(a≠0)的图象与性质
1.二次函数y=ax2+c(a≠0)的图象
(1)
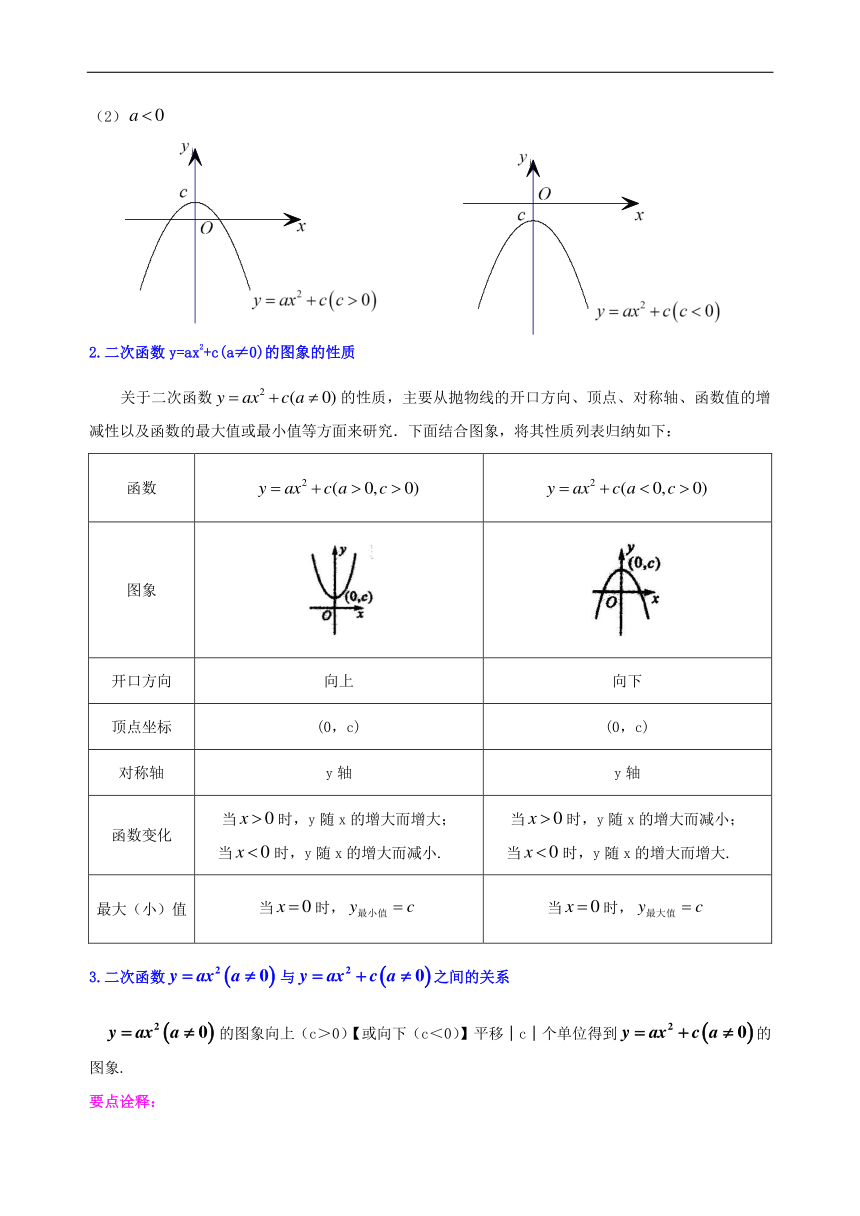
(2)
2.二次函数y=ax2+c(a≠0)的图象的性质
关于二次函数的性质,主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究.下面结合图象,将其性质列表归纳如下:
函数
图象
开口方向
向上
向下
顶点坐标
(0,c)
(0,c)
对称轴
y轴
y轴
函数变化
当时,y随x的增大而增大;
当时,y随x的增大而减小.
当时,y随x的增大而减小;
当时,y随x的增大而增大.
最大(小)值
当时,
当时,
3.二次函数与之间的关系
的图象向上(c>0)【或向下(c<0)】平移│c│个单位得到的图象.
要点诠释:
抛物线的对称轴是y轴,顶点坐标是(0,c),与抛物线的形状相同.
函数的图象是由函数的图象向上(或向下)平移个单位得到的,顶点坐标为(0,c).
抛物线y=ax2(a≠0)的对称轴、最值与顶点密不可分,其对称轴即为过顶点且与x轴垂直的一条直线,其顶点横坐标x=0,抛物线平移不改变抛物线的形状,即a的值不变,只是位置发生变化而已.
【典型例题】
类型一、二次函数y=ax2(a≠0)的图象与性质
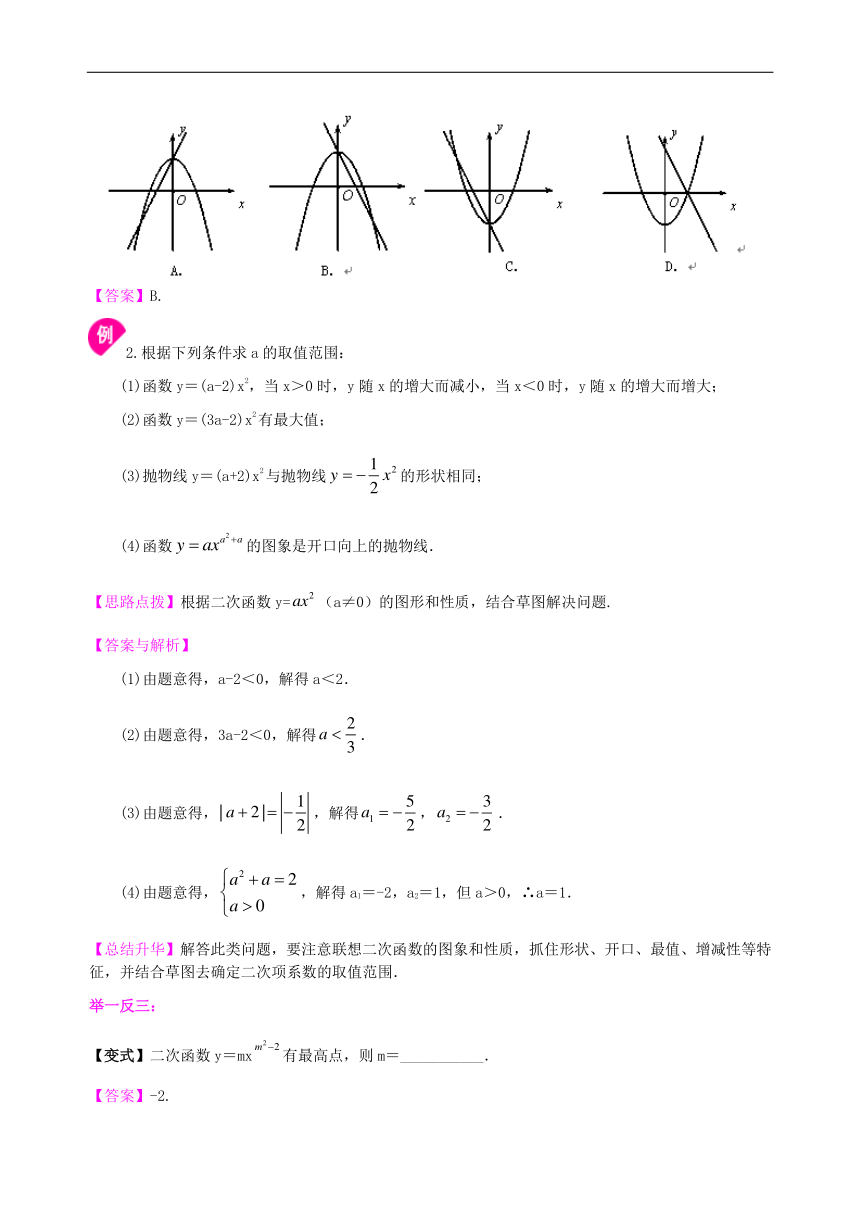
1.(2019?宁夏)已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
A. B. C. D.
【思路点拨】本题可先由一次函数y=ax图象得到字母系数的正负,再与二次函数y=ax2的图象相比较看是否一致.(也可以先固定二次函数y=ax2图象中a的正负,再与一次函数比较.)
【答案】C;
【解析】A、函数y=ax中,a>0,y=ax2中,a>0,但当x=1时,两函数图象有交点(1,a),故A错误;
B、函数y=ax中,a<0,y=ax2中,a>0,故B错误;
C、函数y=ax中,a<0,y=ax2中,a<0,但当x=1时,两函数图象有交点(1,a),故C正确;
D、函数y=ax中,a>0,y=ax2中,a<0,故D错误.
故选:C.
【总结升华】解此类题的基本方法有两种:方法一,根据选项逐个验证;方法二,分a>0和a<0两种情况讨论直接找答案.但要注意图象的交点情况.
举一反三:
【变式】在同一平面直角坐标系中,一次函数与二次函数的图象大致为( ).
【答案】B.
2.根据下列条件求a的取值范围:
(1)函数y=(a-2)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大;
(2)函数y=(3a-2)x2有最大值;
(3)抛物线y=(a+2)x2与抛物线的形状相同;
(4)函数的图象是开口向上的抛物线.
【思路点拨】根据二次函数y=(a≠0)的图形和性质,结合草图解决问题.
【答案与解析】
(1)由题意得,a-2<0,解得a<2.
(2)由题意得,3a-2<0,解得.
(3)由题意得,,解得,.
(4)由题意得,,解得a1=-2,a2=1,但a>0,∴a=1.
【总结升华】解答此类问题,要注意联想二次函数的图象和性质,抓住形状、开口、最值、增减性等特征,并结合草图去确定二次项系数的取值范围.
举一反三:
【变式】二次函数y=mx有最高点,则m=___________.
【答案】-2.
3. 二次函数的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2019在y轴的正半轴上,点B1,B2,B3,…,B2019在二次函数位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2019B2019A2019都为等边三角形,求△A2019B2019A2019的边长.
【思路点拨】分别求出△A0A1B1,△A1A2B2,△A2A3B3的边长,找出边长的变化规律.
【答案与解析】
如图所示,作B1C1⊥y轴,垂足为C1.
∵△A0A1B1为等边三角形,∴∠A0B1C1=30°.
设A0C1=a,则A0B1=2a,B1C1=.∴B1(,),
∴,∴,∴.
作B2C2⊥y轴,设A1C2=m,则A1B2=2m,C2B2=m,
∴.
∴.
∴2m2-m-1=0,
即(2m+1)(m-1)=0,∴m=1或(舍).
∴A1B2=2.
同理可求A2B3=3,A3B4=4,…
∴△A2019B2019A2019的边长为2019.
【总结升华】在△A0A1B1,△A1A2B2,△A2A3B3中,运用勾股定理表示出B1、B2、B3的坐标,利用抛物线解析式建立等式是关键.
类型二、二次函数y=ax2+c(a≠0)的图象与性质
4.(2019?江阴市校级二模)关于二次函数y=2x2+3,下列说法中正确的是( )
A. 它的开口方向是向下;
B. 当x<﹣1时,y随x的增大而减小;
C. 它的对称轴是x=2;
D. 当x=0时,y有最大值是3.
【答案】B.
【解析】
A、∵二次函数y=2x2+3中,x=2>0,∴此抛物线开口向上,故本选项错误;
B、∵抛物线的对称轴x=﹣=0,∴当x<﹣1时函数图象在对称轴左侧,y随x的增大而减小,故本选项正确;
C、抛物线的对称轴为x=0,故本选项错误;
D、∵抛物线开口向上,∴此函数有最小值,故本选项错误.
故选B.
【总结升华】本题考查了二次函数的性质,主要涉及开口方向,对称轴,与y轴的交点坐标,最值问题,熟记二次函数的性质是解题的关键.
举一反三:
【变式】如图所示,抛物线交x轴于G、F,交y轴于点D,在x轴上方的抛物线上有两点B、E,它们关于y轴对称,点G、B在y轴左侧,BA⊥OG于点A,BC⊥OD于点C.四边形OABC与四边形ODEF的面积分别为6和10,则△ABG与△BCD的面积之和为________.
【答案】4.(提示:10-6=4.)
5.有一个抛物线形的拱形隧道,隧道的最大高度为6m,跨度为8m,把它放在如图所示的平面直角坐标系中. (1)求这条抛物线所对应的函数关系式; (2)若要在隧道壁上点P(如图)安装一盏照明灯,灯离地面高4.5m.求灯与点B的距离.
【思路点拨】(1)根据抛物线在坐标系的位置可设解析式:y=ax2+6,把点A(-4,0)代入即可;(2)灯离地面高4.5m,即y=4.5时,求x的值,再根据P点坐标,勾股定理求PB的值.
【答案与解析】
解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<0), ∵点A(-4,0)或B(4,0)在抛物线上, ∴0=a?(-4)2+6, 16a+6=0,16a=-6, . 故抛物线的函数关系式为.
(2)过点P作PQ⊥AB于Q,连接PB,则PQ=4.5m. 将y=4.5代入,得x=±2. ∴P(-2,4.5),Q(-2,0), 于是|PQ|=4.5,|BQ|=6, 从而|PB|= 所以照明灯与点B的距离为7.5m.
【总结升华】本题考查建系确定点的坐标,应用二次函数解决实际问题,建系的方法不唯一.
二次函数y=ax2(a≠0)的图象与性质—巩固练习(提高)
【巩固练习】
一、选择题 1.若抛物线的开口向下,则m的值为( ).
A.3 B.-3 C. D.
2.抛物线的顶点坐标,对称轴分别是( ).
A.(2,0),直线x=-4 B.(-2,0),直线x=4
C.(1,3),直线x=0 D.(0,-4),直线x=0
3.两条抛物线与在同一坐标系内,下列说法中不正确的是( )
A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值
4.关于,,的图像,下列说法中不正确的是( )
A.顶点相同 B.对称轴相同 C.图像形状相同 D.最低点相同
5.(2019?市北区一模)在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( ).
A. B. C. D.
6.图中是一个横断面为抛物线形状的拱桥,当水面在处时,拱顶(拱桥洞的最高点)离水面2 m,
水面宽4 m.如图所示建立平面直角坐标系,则抛物线的解析式是( ).
A. B. C. D.
二、填空题
7.抛物线的开口 ,对称轴是 ,顶点坐标是 .
8.将抛物线向上平移5个单位后,得到的抛物线的解析式是____ ____.
9.已知(x1,y1),(x2,y2)是抛物线(a≠0)上的两点.当时,,则a的取值范围是________.
10. (2019?巴中模拟)对于二次函数y=ax2,已知当x由1增加到2时,函数值减少4,则常数a的值是 .
11.抛物线与的形状相同,其顶点坐标为(0,1),则其解析式为 .
12.如图,⊙O的半径为2,是函数的图象,是函数的图象,则阴影部分的面积是 .
三、解答题
13.(2019?仙桃)如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为多少米?
14.已知直线与x轴交于点A,抛物线的顶点平移后与点A重合.
(1)求平移后的抛物线C的解析式;
(2)若点B(,),C(,)在抛物线C上,且,试比较,的大小.
15. 已知正方形周长为Ccm,面积为S cm2.
(1)求S和C之间的函数关系式,并画出图象;
(2)根据图象,求出S=1 cm2时,正方形的周长;
(3)根据图象,求出C取何值时,S≥4 cm2.
【答案与解析】
一、选择题 1.【答案】D;
【解析】依题意得m2-10=2且2+m<0,即m=±,且m<-2,所以.
2.【答案】D;
【解析】由函数y=ax2+c的图象性质可得.
3.【答案】D;
【解析】两条抛物线一个开口向上,有最小值,另一个开口向下,有最大值.
4.【答案】C;
【解析】根据图象y=ax2的性质,三个函数的顶点都是原点、对称轴都是y轴、最低点都为0,由于a值不同,所以他们的图像形状不同.
5.【答案】D;
【解析】A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.故选:D.
6.【答案】C;
【解析】依题意知点(2,-2)在y=ax2图象上,所以-2=a×22,.所以.
二、填空题
7.【答案】向下;y轴;(0,0).
8.【答案】;
【解析】根据平移规律:上加下减.
9.【答案】a<0 ;
【解析】∵x2<x1<0,y2<y1,所以y随x的增大而增大,结合图象知,抛物线开口向下.
10.【答案】.
【解析】当x=1时,y=ax2=a;
当x=2时,y=ax2=4a,
所以a﹣4a=4,解得a=.
故答案为:.
11.【答案】y=3x2+1或y=-3x2+1.
【解析】形状相同,说明相同,所以a=,再将顶点坐标(0,1)代入即可求出c.
12.【答案】2π;
【解析】根据抛物线的对称性,将x轴下方的阴影翻到上方,正好形成一个半圆形,半圆的面积为.
三、解答题
13.【答案与解析】
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(﹣2,0),
到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣1代入抛物线解析式得出:
﹣1=﹣0.5x2+2,
解得:x=,
所以水面宽度增加到米,
故答案为:.
14.【解析】
(1)∵,
∴令,则,
∴,即抛物线C的顶点坐标为,
又抛物线C是由抛物线平移得到的,
∴,
∴抛物线C的解析式为.
(2)由(1)知,抛物线C的对称轴为直线.
∵,
∴当时,y随x的增大而减小,
又∵,∴.
15.【解析】
解:(1)由题意,得.
列表、描点、连线,图象如图:
(2)根据图象得S=1cm2时,正方形的周长是4cm.
(3)根据图象得,当C≥8cm时,S≥4 cm2.
【学习目标】
1.经历探索二次函数y=ax2和y=ax2+c的图象的作法和性质的过程,进一步获得将表格、表达式、图象三者联系起来的经验.
2.会作出y=ax2和y=ax2+c的图象,并能比较它们与y=x2的异同,理解a与c对二次函数图象的影响.
3.能说出y=ax2+c与y=ax2图象的开口方向、对称轴和顶点坐标.
4.体会二次函数是某些实际问题的数学模型.
5.掌握二次函数y=ax2(a≠0)与y=ax2+c (a≠0)的图象之间的关系.
【要点梳理】
要点一、二次函数y=ax2(a≠0)的图象与性质
1.二次函数y=ax2(a≠0)的图象
二次函数y=ax2的图象(如图),是一条关于y轴对称的曲线,这样的曲线叫做抛物线.
抛物线y=ax2(a≠0)的对称轴是y轴,它的顶点是坐标原点.当a> 0时,抛物线的开口向上,顶点是它的最低点;当a<0时,抛物线的开口向下,顶点是它的最高点.
2.二次函数y=ax2(a≠0)的图象的画法——描点法
描点法画图的基本步骤:列表、描点、连线.
(1)列表:选择自变量取值范围内的一些适当的x的值,求出相应的y值,填入表中.(自变量x的值写在第一行,其值从左到右,从小到大.)
(2)描点:以表中每对x和y的值为坐标,在坐标平面内准确描出相应的点.一般地,点取的越多,图象就越准确.
(3)连线:按照自变量的值由小到大的顺序,把所描的点用平滑的曲线连结起来.
要点诠释:
(1)用描点法画二次函数y=ax2(a≠0)的图象时,应在顶点的左、右两侧对称地选取自变量x的值,然后计算出对应的y值.
(2)二次函数y=ax2(a≠0)的图象,是轴对称图形,对称轴是y轴.y=ax2(a≠0)是最简单的二次函数.
(3)画草图时应抓住以下几点:开口方向,对称轴,顶点,与轴的交点,与轴的交点.
3.二次函数y=ax2(a≠0)的图象的性质
二次函数y=ax2(a≠0)的图象的性质,见下表:
函数
图象
开口方向
顶点坐标
对称轴
函数变化
最大(小)值
y=ax2
a>0
向上
(0,0)
y轴
x>0时,y随x增大而增大;
x<0时,y随x增大而减小.
当x=0时,y最小=0
y=ax2
a<0
向下
(0,0)
y轴
x>0时,y随x增大而减小;
x<0时,y随x增大而增大.
当x=0时,y最大=0
要点诠释: 顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. │a│相同,抛物线的开口大小、形状相同.
│a│越大,开口越小,图象两边越靠近y轴,│a│越小,开口越大,图象两边越靠近x轴.
要点二、二次函数y=ax2+c(a≠0)的图象与性质
1.二次函数y=ax2+c(a≠0)的图象
(1)
(2)
2.二次函数y=ax2+c(a≠0)的图象的性质
关于二次函数的性质,主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究.下面结合图象,将其性质列表归纳如下:
函数
图象
开口方向
向上
向下
顶点坐标
(0,c)
(0,c)
对称轴
y轴
y轴
函数变化
当时,y随x的增大而增大;
当时,y随x的增大而减小.
当时,y随x的增大而减小;
当时,y随x的增大而增大.
最大(小)值
当时,
当时,
3.二次函数与之间的关系
的图象向上(c>0)【或向下(c<0)】平移│c│个单位得到的图象.
要点诠释:
抛物线的对称轴是y轴,顶点坐标是(0,c),与抛物线的形状相同.
函数的图象是由函数的图象向上(或向下)平移个单位得到的,顶点坐标为(0,c).
抛物线y=ax2(a≠0)的对称轴、最值与顶点密不可分,其对称轴即为过顶点且与x轴垂直的一条直线,其顶点横坐标x=0,抛物线平移不改变抛物线的形状,即a的值不变,只是位置发生变化而已.
【典型例题】
类型一、二次函数y=ax2(a≠0)的图象与性质
1.(2019?宁夏)已知a≠0,在同一直角坐标系中,函数y=ax与y=ax2的图象有可能是( )
A. B. C. D.
【思路点拨】本题可先由一次函数y=ax图象得到字母系数的正负,再与二次函数y=ax2的图象相比较看是否一致.(也可以先固定二次函数y=ax2图象中a的正负,再与一次函数比较.)
【答案】C;
【解析】A、函数y=ax中,a>0,y=ax2中,a>0,但当x=1时,两函数图象有交点(1,a),故A错误;
B、函数y=ax中,a<0,y=ax2中,a>0,故B错误;
C、函数y=ax中,a<0,y=ax2中,a<0,但当x=1时,两函数图象有交点(1,a),故C正确;
D、函数y=ax中,a>0,y=ax2中,a<0,故D错误.
故选:C.
【总结升华】解此类题的基本方法有两种:方法一,根据选项逐个验证;方法二,分a>0和a<0两种情况讨论直接找答案.但要注意图象的交点情况.
举一反三:
【变式】在同一平面直角坐标系中,一次函数与二次函数的图象大致为( ).
【答案】B.
2.根据下列条件求a的取值范围:
(1)函数y=(a-2)x2,当x>0时,y随x的增大而减小,当x<0时,y随x的增大而增大;
(2)函数y=(3a-2)x2有最大值;
(3)抛物线y=(a+2)x2与抛物线的形状相同;
(4)函数的图象是开口向上的抛物线.
【思路点拨】根据二次函数y=(a≠0)的图形和性质,结合草图解决问题.
【答案与解析】
(1)由题意得,a-2<0,解得a<2.
(2)由题意得,3a-2<0,解得.
(3)由题意得,,解得,.
(4)由题意得,,解得a1=-2,a2=1,但a>0,∴a=1.
【总结升华】解答此类问题,要注意联想二次函数的图象和性质,抓住形状、开口、最值、增减性等特征,并结合草图去确定二次项系数的取值范围.
举一反三:
【变式】二次函数y=mx有最高点,则m=___________.
【答案】-2.
3. 二次函数的图象如图所示,点A0位于坐标原点,点A1,A2,A3,…,A2019在y轴的正半轴上,点B1,B2,B3,…,B2019在二次函数位于第一象限的图象上,若△A0B1A1,△A1B2A2,△A2B3A3,…,△A2019B2019A2019都为等边三角形,求△A2019B2019A2019的边长.
【思路点拨】分别求出△A0A1B1,△A1A2B2,△A2A3B3的边长,找出边长的变化规律.
【答案与解析】
如图所示,作B1C1⊥y轴,垂足为C1.
∵△A0A1B1为等边三角形,∴∠A0B1C1=30°.
设A0C1=a,则A0B1=2a,B1C1=.∴B1(,),
∴,∴,∴.
作B2C2⊥y轴,设A1C2=m,则A1B2=2m,C2B2=m,
∴.
∴.
∴2m2-m-1=0,
即(2m+1)(m-1)=0,∴m=1或(舍).
∴A1B2=2.
同理可求A2B3=3,A3B4=4,…
∴△A2019B2019A2019的边长为2019.
【总结升华】在△A0A1B1,△A1A2B2,△A2A3B3中,运用勾股定理表示出B1、B2、B3的坐标,利用抛物线解析式建立等式是关键.
类型二、二次函数y=ax2+c(a≠0)的图象与性质
4.(2019?江阴市校级二模)关于二次函数y=2x2+3,下列说法中正确的是( )
A. 它的开口方向是向下;
B. 当x<﹣1时,y随x的增大而减小;
C. 它的对称轴是x=2;
D. 当x=0时,y有最大值是3.
【答案】B.
【解析】
A、∵二次函数y=2x2+3中,x=2>0,∴此抛物线开口向上,故本选项错误;
B、∵抛物线的对称轴x=﹣=0,∴当x<﹣1时函数图象在对称轴左侧,y随x的增大而减小,故本选项正确;
C、抛物线的对称轴为x=0,故本选项错误;
D、∵抛物线开口向上,∴此函数有最小值,故本选项错误.
故选B.
【总结升华】本题考查了二次函数的性质,主要涉及开口方向,对称轴,与y轴的交点坐标,最值问题,熟记二次函数的性质是解题的关键.
举一反三:
【变式】如图所示,抛物线交x轴于G、F,交y轴于点D,在x轴上方的抛物线上有两点B、E,它们关于y轴对称,点G、B在y轴左侧,BA⊥OG于点A,BC⊥OD于点C.四边形OABC与四边形ODEF的面积分别为6和10,则△ABG与△BCD的面积之和为________.
【答案】4.(提示:10-6=4.)
5.有一个抛物线形的拱形隧道,隧道的最大高度为6m,跨度为8m,把它放在如图所示的平面直角坐标系中. (1)求这条抛物线所对应的函数关系式; (2)若要在隧道壁上点P(如图)安装一盏照明灯,灯离地面高4.5m.求灯与点B的距离.
【思路点拨】(1)根据抛物线在坐标系的位置可设解析式:y=ax2+6,把点A(-4,0)代入即可;(2)灯离地面高4.5m,即y=4.5时,求x的值,再根据P点坐标,勾股定理求PB的值.
【答案与解析】
解:(1)由题意,设抛物线所对应的函数关系为y=ax2+6(a<0), ∵点A(-4,0)或B(4,0)在抛物线上, ∴0=a?(-4)2+6, 16a+6=0,16a=-6, . 故抛物线的函数关系式为.
(2)过点P作PQ⊥AB于Q,连接PB,则PQ=4.5m. 将y=4.5代入,得x=±2. ∴P(-2,4.5),Q(-2,0), 于是|PQ|=4.5,|BQ|=6, 从而|PB|= 所以照明灯与点B的距离为7.5m.
【总结升华】本题考查建系确定点的坐标,应用二次函数解决实际问题,建系的方法不唯一.
二次函数y=ax2(a≠0)的图象与性质—巩固练习(提高)
【巩固练习】
一、选择题 1.若抛物线的开口向下,则m的值为( ).
A.3 B.-3 C. D.
2.抛物线的顶点坐标,对称轴分别是( ).
A.(2,0),直线x=-4 B.(-2,0),直线x=4
C.(1,3),直线x=0 D.(0,-4),直线x=0
3.两条抛物线与在同一坐标系内,下列说法中不正确的是( )
A.顶点相同 B.对称轴相同 C.开口方向相反 D.都有最小值
4.关于,,的图像,下列说法中不正确的是( )
A.顶点相同 B.对称轴相同 C.图像形状相同 D.最低点相同
5.(2019?市北区一模)在同一直角坐标系中,函数y=kx2﹣k和y=kx+k(k≠0)的图象大致是( ).
A. B. C. D.
6.图中是一个横断面为抛物线形状的拱桥,当水面在处时,拱顶(拱桥洞的最高点)离水面2 m,
水面宽4 m.如图所示建立平面直角坐标系,则抛物线的解析式是( ).
A. B. C. D.
二、填空题
7.抛物线的开口 ,对称轴是 ,顶点坐标是 .
8.将抛物线向上平移5个单位后,得到的抛物线的解析式是____ ____.
9.已知(x1,y1),(x2,y2)是抛物线(a≠0)上的两点.当时,,则a的取值范围是________.
10. (2019?巴中模拟)对于二次函数y=ax2,已知当x由1增加到2时,函数值减少4,则常数a的值是 .
11.抛物线与的形状相同,其顶点坐标为(0,1),则其解析式为 .
12.如图,⊙O的半径为2,是函数的图象,是函数的图象,则阴影部分的面积是 .
三、解答题
13.(2019?仙桃)如图是一个横断面为抛物线形状的拱桥,当水面宽4米时,拱顶(拱桥洞的最高点)离水面2米,水面下降1米时,水面的宽度为多少米?
14.已知直线与x轴交于点A,抛物线的顶点平移后与点A重合.
(1)求平移后的抛物线C的解析式;
(2)若点B(,),C(,)在抛物线C上,且,试比较,的大小.
15. 已知正方形周长为Ccm,面积为S cm2.
(1)求S和C之间的函数关系式,并画出图象;
(2)根据图象,求出S=1 cm2时,正方形的周长;
(3)根据图象,求出C取何值时,S≥4 cm2.
【答案与解析】
一、选择题 1.【答案】D;
【解析】依题意得m2-10=2且2+m<0,即m=±,且m<-2,所以.
2.【答案】D;
【解析】由函数y=ax2+c的图象性质可得.
3.【答案】D;
【解析】两条抛物线一个开口向上,有最小值,另一个开口向下,有最大值.
4.【答案】C;
【解析】根据图象y=ax2的性质,三个函数的顶点都是原点、对称轴都是y轴、最低点都为0,由于a值不同,所以他们的图像形状不同.
5.【答案】D;
【解析】A、由一次函数y=kx+k的图象可得:k>0,此时二次函数y=kx2﹣kx的图象应该开口向上,错误;
B、由一次函数y=kx+k图象可知,k>0,此时二次函数y=kx2﹣kx的图象顶点应在y轴的负半轴,错误;
C、由一次函数y=kx+k可知,y随x增大而减小时,直线与y轴交于负半轴,错误;
D、正确.故选:D.
6.【答案】C;
【解析】依题意知点(2,-2)在y=ax2图象上,所以-2=a×22,.所以.
二、填空题
7.【答案】向下;y轴;(0,0).
8.【答案】;
【解析】根据平移规律:上加下减.
9.【答案】a<0 ;
【解析】∵x2<x1<0,y2<y1,所以y随x的增大而增大,结合图象知,抛物线开口向下.
10.【答案】.
【解析】当x=1时,y=ax2=a;
当x=2时,y=ax2=4a,
所以a﹣4a=4,解得a=.
故答案为:.
11.【答案】y=3x2+1或y=-3x2+1.
【解析】形状相同,说明相同,所以a=,再将顶点坐标(0,1)代入即可求出c.
12.【答案】2π;
【解析】根据抛物线的对称性,将x轴下方的阴影翻到上方,正好形成一个半圆形,半圆的面积为.
三、解答题
13.【答案与解析】
解:建立平面直角坐标系,设横轴x通过AB,纵轴y通过AB中点O且通过C点,则通过画图可得知O为原点,
抛物线以y轴为对称轴,且经过A,B两点,OA和OB可求出为AB的一半2米,抛物线顶点C坐标为(0,2),
通过以上条件可设顶点式y=ax2+2,其中a可通过代入A点坐标(﹣2,0),
到抛物线解析式得出:a=﹣0.5,所以抛物线解析式为y=﹣0.5x2+2,
当水面下降1米,通过抛物线在图上的观察可转化为:
当y=﹣1时,对应的抛物线上两点之间的距离,也就是直线y=﹣1与抛物线相交的两点之间的距离,
可以通过把y=﹣1代入抛物线解析式得出:
﹣1=﹣0.5x2+2,
解得:x=,
所以水面宽度增加到米,
故答案为:.
14.【解析】
(1)∵,
∴令,则,
∴,即抛物线C的顶点坐标为,
又抛物线C是由抛物线平移得到的,
∴,
∴抛物线C的解析式为.
(2)由(1)知,抛物线C的对称轴为直线.
∵,
∴当时,y随x的增大而减小,
又∵,∴.
15.【解析】
解:(1)由题意,得.
列表、描点、连线,图象如图:
(2)根据图象得S=1cm2时,正方形的周长是4cm.
(3)根据图象得,当C≥8cm时,S≥4 cm2.
