北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第6讲 二次函数y=a(x-h)^2+ k(a≠0)的图像与性质(提高)含答案
文档属性
| 名称 | 北师大版初中数学九年级下册知识讲解,巩固练习(教学资料,补习资料):第6讲 二次函数y=a(x-h)^2+ k(a≠0)的图像与性质(提高)含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 229.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 00:00:00 | ||
图片预览

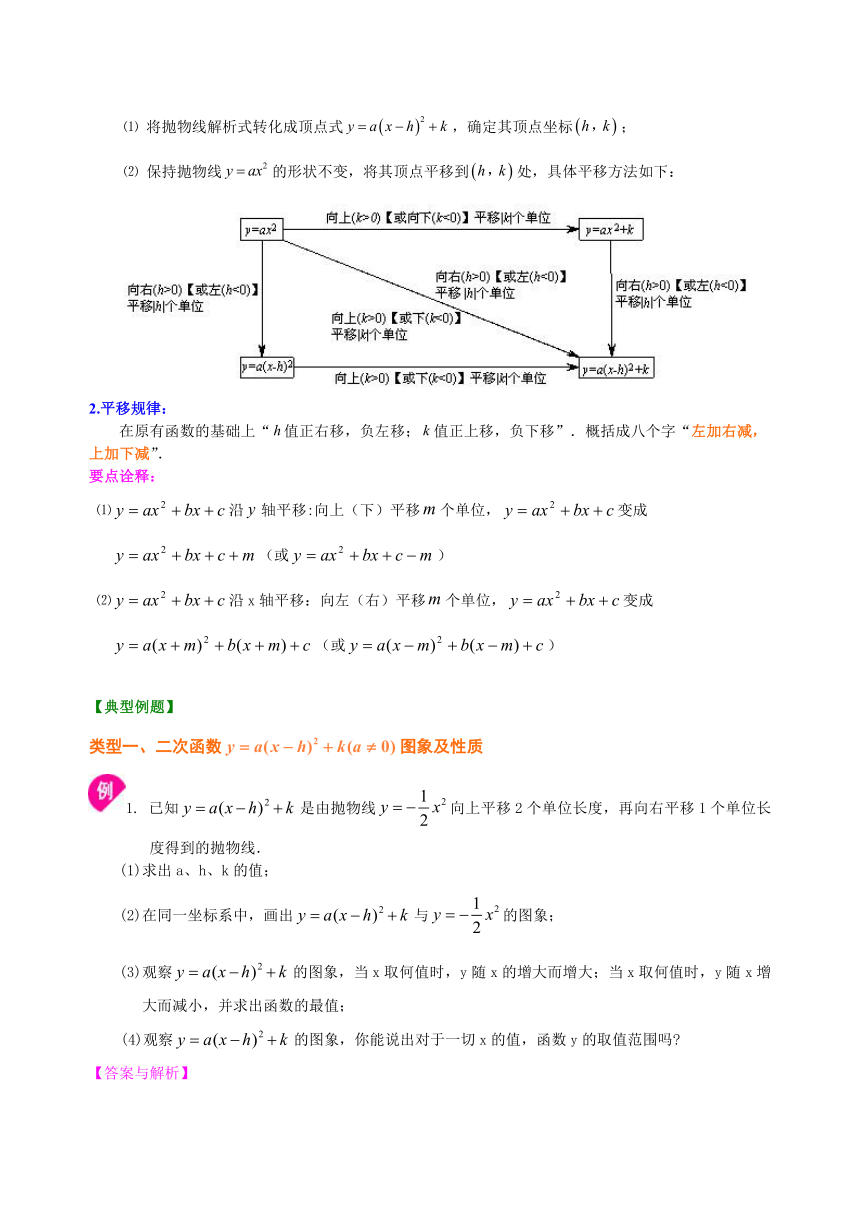



文档简介
二次函数y=a(x-h)2+k(a≠0)的图象与性质—知识讲解(提高)
【学习目标】
1.会用描点法画出二次函数(a、h、k常数,a≠0)的图象.掌握抛物线与图象之间的关系;
2.熟练掌握函数的有关性质,并能用函数的性质解决一些实际问题;
3.经历探索的图象及性质的过程,体验与、、之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴沿轴平移:向上(下)平移个单位,变成
(或)
⑵沿x轴平移:向左(右)平移个单位,变成(或)
【典型例题】
类型一、二次函数图象及性质
1. 已知是由抛物线向上平移2个单位长度,再向右平移1个单位长度得到的抛物线.
(1)求出a、h、k的值;
(2)在同一坐标系中,画出与的图象;
(3)观察的图象,当x取何值时,y随x的增大而增大;当x取何值时,y随x增大而减小,并求出函数的最值;
(4)观察的图象,你能说出对于一切x的值,函数y的取值范围吗?
【答案与解析】
(1)∵ 抛物线向上平移2个单位长度,
再向右平移1个单位长度得到的抛物线是,
∴ ,,.
(2)函数与的图象如图所示.
(3)观察的图象知,当时,y随x的增大而增大;
当时,y随x增大而减小,当x=1时,函数y有最大值是2.
(4)由图象知,对于一切x的值,总有函数值y≤2.
【总结升华】先根据平移的性质求出抛物线平移后的抛物线的解析式,再对比得到a、h、k的值,然后画出图象,由图象回答问题.
举一反三:
【变式】把二次函数的图象先向左平移2个单位,再向上平移4个单位,得到二次函数的图象.
(1)试确定a、h、k的值;
(2)指出二次函数的开口方向,对称轴和顶点坐标,分析函数的增减性.
【答案】(1).(2)开口向下,对称轴x=1, 顶点坐标为(1,-5),
当x≥1时,y随x的增大而减小; 当x<1时,y随x的增大而增大.
2. 已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A.0 B.1 C.2 D.3
【答案】D;
【解析】函数 的图象如图:
,
根据图象知道当y=3时,对应成立的x恰好有三个,
∴k=3.
故选D.
【总结升华】此题主要考查了利用二次函数的图象解决交点问题,解题的关键是把解方程的问题转换为根据函数图象找交点的问题.
类型二、二次函数性质的综合应用
3.(2019秋?滨海县期末)已知:二次函数y=x2﹣4x+3.
(1)求出该二次函数图象的对称轴和顶点坐标;
(2)求出该抛物线与x轴的交点坐标;
(3)当x取何值时,y<0.
【解析】解:(1)∵y=x2﹣4x+3,
∴y=(x﹣2)2﹣1,
∴对称轴为:直线x=2,
∴顶点(2,﹣1);
(2)令y=0,
则,x2﹣4x+3=0,
∴(x﹣1)(x﹣3)=0,
∴x1=1,x2=3,
∴与x轴的交点坐标为(1,0),(3,0);
(3)当1<x<3时,y<0.
【总结升华】本题考查了二次函数的性质,抛物线与x轴坐标的求解方法,二次函数与不等式,熟记性质并把函数解析式整理成顶点式形式求解更简便.
举一反三:
【变式】(2019秋?岑溪市期末)已知抛物线y=2(x﹣1)2﹣8.
(1)直接写出它的顶点坐标: ,对称轴: ;
(2)x取何值时,y随x增大而增大?
【答案与解析】
解:(1)抛物线y=2(x﹣1)2﹣8的顶点坐标为(1,﹣8),对称轴为直线x=1;
故答案为(1,﹣8),直线x=1;
(2)当x>1时,y随x增大而增大.
4. 如图所示,抛物线的顶点为C,与y轴交点为A,过点A作y轴的垂线,交抛物线于另一点B.
(1)求直线AC的解析式;
(2)求△ABC的面积;
(3)当自变量x满足什么条件时,有?
【答案与解析】
(1)由知抛物线顶点C(-1,0),令x=0,得,
∴ .由待定系数法可求出,,
∴ .
(2)∵ 抛物线的对称轴为x=-1,根据抛物线对称性知.
∴ .
(3)根据图象知或时,有.
【总结升华】 图象都经过A点和C点,说明A点、C点同时出现在两个图象上,A、C两点的坐标均满足两个函数的解析式,解答这类题时,要画出函数图象,结合几何图形的性质,运用数形结合的思想和抛物线的对称性,特别要慎重处理平面直角坐标系中的坐标(数)与线段长度(形)之间的关系,不要出现符号上的错误,充分利用函数图象弄清函数值与自变量的关系,利用图象比较函数值的大小,或根据函数值的大小,确定自变量的变化范围.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(提高)
【巩固练习】
一、选择题 1. 不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )
A.在y=x直线上 B.在直线y=-x上 C.在x轴上 D.在y轴上
2.二次函数的最小值是( ).
A.-2 B.2 C.-l D.1
3.如图所示,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( ).
A. B. C. D.,
第3题 第5题
4.(2019?牡丹江)将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( ).
A.(0,2) B.(0,3) C.(0,4) D.(0,7)
5.如图所示,抛物线的顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( ).
A. B. C. D.
6.若二次函数.当≤l时,随的增大而减小,则的取值范围是( )
A.=l B.>l C.≥l D.≤l
二、填空题
7.(2019?巴中模拟)抛物线y=x2+2x+7的开口向 ,对称轴是 ,顶点是 .
8.若点A(3,-4)在函数的图象上,则_ _.这个抛物线的对称轴是 ;
点A关于抛物线对称轴的对称点是 .
9.如果把抛物线向上平移-3个单位,再向右平移3个单位长度后得到抛物线,则求的值为 ;的值为 .
10.请写出一个二次函数,图象顶点为(-1,2),且不论x取何值,函数值y恒为正数.则此二次函数为______ __.
11.若二次函数中的x取值为2≤x≤5,则该函数的最大值为 ;最小值为 .
12.已知抛物线y=x2+x+b2经过点,则y1的值是_____.
三、解答题
13.抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周长.
14.(2019秋?湘西州期末)已知二次函数y=﹣x2+2(m﹣1)x+2m﹣m2的图象关于y轴对称,其顶点为A,与x轴两交点为B、C.
(1)求B、C两点的坐标.
(2)求△ABC的面积.
15.如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.
(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
【答案与解析】
一、选择题 1.【答案】B;
【解析】抛物线y=a(x+m)2+m(a≠0)的顶点为(-m,m),所以顶点在直线y=-x上.
2.【答案】B;
【解析】当时,二次函数有最小值为2.
3.【答案】B;
【解析】由两抛物线对称轴相同可知,且由图象知,,.
4.【答案】B;
【解析】抛物线y=(x﹣1)2+3的顶点坐标为(1,3),
把点(1,3)向左平移1个单位得到点的坐标为(0,3),
所以平移后抛物线解析式为y=x2+3,
所以得到的抛物线与y轴的交点坐标为(0,3).
故选:B.
5.【答案】C;
【解析】由顶点坐标P(1,3)知抛物线的对称轴为直线,因此当时,y随x的增大而减小.
6.【答案】C;
【解析】画出草图进行分析得出结论.
二、填空题
7.【答案】上,x=﹣1,(﹣1,6).
【解析】∵y=x2+2x+7,
而a=1>0,
∴开口方向向上,
∵y=y=x2+2x+7=(x2+2x+1)+6=(x+1)2+6,
∴对称轴是x=﹣1,顶点坐标是(﹣1,6).
8.【答案】5或1; 直线x=5或直线x=1; 或(-1,-4);
【解析】因为点A(3,-4)在函数的图象上,所以把点A(3,-4)代入
函数得或;对称轴是直线x=5或直线x=1;点A关于抛物线对称轴的对称点是或(-1,-4).
9.【答案】 ,;
【解析】抛物线向上平移-3个单位得到,再向右平移3个单位长度得到,即与相同,故,.
10.【答案】 等;
【解析】答案不唯一,只要抛物线开口向上即可,即,所以或等均可.
11.【答案】50;5.
【解析】由于函数的顶点坐标为(1,2),,
当时,y随x的增大而增大,
当x=5时,函数在2≤x≤5范围内的最大值为50;
当x=2时,函数的最小值为.
12.【答案】;
【解析】把代入y=x2+x+b2得,,
,代入即可求得.
三、解答题
13.【答案与解析】
∵ 抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,
∴ A(2,0),B(0,12),
∴ S△AOB=12,△AOB的周长为14十.
14.【答案与解析】
解:由二次函数y=﹣x2+2(m﹣1)x+2m﹣m2的图象关于y轴对称,得
m﹣1=0.
解得m=1.
函数解析式为y=﹣x2+1,
当y=0时,﹣x2+1=0.
解得x1=﹣1,x2=1,
即B(﹣1,0),C(1,0);
(2)当x=0时,y=1,即A(0,1),
S△ABC=×2×1=1.
15.【答案与解析】
(1)连接ME,设MN交BE交于P,
根据题意得MB=ME,MN⊥BE.
过N作NF⊥AB于F,在Rt△MBP和Rt△MNF中,∠MBP+∠BMN=90°,
∠FNM+∠BMN=90°,∠MBP=∠MNF,又AB=FN,Rt△EBA≌Rt△MNF,MF=AE=x.
在Rt△AME中,由勾股定理得
ME2=AE2+AM2,
所以MB2=x2+AM2,即(2-AM)2=x2+AM2,解得AM=1-x2.
所以四边形ADNM的面积
S=×2=AM+AM+MF=2AM+AE=2(1-x2)+x=-x2+x+2.
即所求关系式为S=-x2+x+2.
(2)S=-x2+x+2=-(x2-2x+1)+=-(x-1)2+.
当AE=x=1时,四边形ADNM的面积S的值最大,此时最大值是.
【学习目标】
1.会用描点法画出二次函数(a、h、k常数,a≠0)的图象.掌握抛物线与图象之间的关系;
2.熟练掌握函数的有关性质,并能用函数的性质解决一些实际问题;
3.经历探索的图象及性质的过程,体验与、、之间的转化过程,深刻理解数学建模思想及数形结合的思想方法.
【要点梳理】
要点一、函数与函数的图象与性质
1.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
2.函数的图象与性质
的符号
开口方向
顶点坐标
对称轴
性质
向上
x=h
时,随的增大而增大;时,随的增大而减小;时,有最小值.
向下
x=h
时,随的增大而减小;时,随的增大而增大;时,有最大值.
要点诠释:
二次函数的图象常与直线、三角形、面积问题结合在一起,借助它的图象与性质.运用数形结合、函数、方程思想解决问题.
要点二、二次函数的平移
1.平移步骤:
⑴ 将抛物线解析式转化成顶点式,确定其顶点坐标;
⑵ 保持抛物线的形状不变,将其顶点平移到处,具体平移方法如下:
2.平移规律:
在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.
要点诠释:
⑴沿轴平移:向上(下)平移个单位,变成
(或)
⑵沿x轴平移:向左(右)平移个单位,变成(或)
【典型例题】
类型一、二次函数图象及性质
1. 已知是由抛物线向上平移2个单位长度,再向右平移1个单位长度得到的抛物线.
(1)求出a、h、k的值;
(2)在同一坐标系中,画出与的图象;
(3)观察的图象,当x取何值时,y随x的增大而增大;当x取何值时,y随x增大而减小,并求出函数的最值;
(4)观察的图象,你能说出对于一切x的值,函数y的取值范围吗?
【答案与解析】
(1)∵ 抛物线向上平移2个单位长度,
再向右平移1个单位长度得到的抛物线是,
∴ ,,.
(2)函数与的图象如图所示.
(3)观察的图象知,当时,y随x的增大而增大;
当时,y随x增大而减小,当x=1时,函数y有最大值是2.
(4)由图象知,对于一切x的值,总有函数值y≤2.
【总结升华】先根据平移的性质求出抛物线平移后的抛物线的解析式,再对比得到a、h、k的值,然后画出图象,由图象回答问题.
举一反三:
【变式】把二次函数的图象先向左平移2个单位,再向上平移4个单位,得到二次函数的图象.
(1)试确定a、h、k的值;
(2)指出二次函数的开口方向,对称轴和顶点坐标,分析函数的增减性.
【答案】(1).(2)开口向下,对称轴x=1, 顶点坐标为(1,-5),
当x≥1时,y随x的增大而减小; 当x<1时,y随x的增大而增大.
2. 已知函数,则使y=k成立的x值恰好有三个,则k的值为( )
A.0 B.1 C.2 D.3
【答案】D;
【解析】函数 的图象如图:
,
根据图象知道当y=3时,对应成立的x恰好有三个,
∴k=3.
故选D.
【总结升华】此题主要考查了利用二次函数的图象解决交点问题,解题的关键是把解方程的问题转换为根据函数图象找交点的问题.
类型二、二次函数性质的综合应用
3.(2019秋?滨海县期末)已知:二次函数y=x2﹣4x+3.
(1)求出该二次函数图象的对称轴和顶点坐标;
(2)求出该抛物线与x轴的交点坐标;
(3)当x取何值时,y<0.
【解析】解:(1)∵y=x2﹣4x+3,
∴y=(x﹣2)2﹣1,
∴对称轴为:直线x=2,
∴顶点(2,﹣1);
(2)令y=0,
则,x2﹣4x+3=0,
∴(x﹣1)(x﹣3)=0,
∴x1=1,x2=3,
∴与x轴的交点坐标为(1,0),(3,0);
(3)当1<x<3时,y<0.
【总结升华】本题考查了二次函数的性质,抛物线与x轴坐标的求解方法,二次函数与不等式,熟记性质并把函数解析式整理成顶点式形式求解更简便.
举一反三:
【变式】(2019秋?岑溪市期末)已知抛物线y=2(x﹣1)2﹣8.
(1)直接写出它的顶点坐标: ,对称轴: ;
(2)x取何值时,y随x增大而增大?
【答案与解析】
解:(1)抛物线y=2(x﹣1)2﹣8的顶点坐标为(1,﹣8),对称轴为直线x=1;
故答案为(1,﹣8),直线x=1;
(2)当x>1时,y随x增大而增大.
4. 如图所示,抛物线的顶点为C,与y轴交点为A,过点A作y轴的垂线,交抛物线于另一点B.
(1)求直线AC的解析式;
(2)求△ABC的面积;
(3)当自变量x满足什么条件时,有?
【答案与解析】
(1)由知抛物线顶点C(-1,0),令x=0,得,
∴ .由待定系数法可求出,,
∴ .
(2)∵ 抛物线的对称轴为x=-1,根据抛物线对称性知.
∴ .
(3)根据图象知或时,有.
【总结升华】 图象都经过A点和C点,说明A点、C点同时出现在两个图象上,A、C两点的坐标均满足两个函数的解析式,解答这类题时,要画出函数图象,结合几何图形的性质,运用数形结合的思想和抛物线的对称性,特别要慎重处理平面直角坐标系中的坐标(数)与线段长度(形)之间的关系,不要出现符号上的错误,充分利用函数图象弄清函数值与自变量的关系,利用图象比较函数值的大小,或根据函数值的大小,确定自变量的变化范围.
二次函数y=a(x-h)2+k(a≠0)的图象与性质—巩固练习(提高)
【巩固练习】
一、选择题 1. 不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )
A.在y=x直线上 B.在直线y=-x上 C.在x轴上 D.在y轴上
2.二次函数的最小值是( ).
A.-2 B.2 C.-l D.1
3.如图所示,直角坐标系中,两条抛物线有相同的对称轴,下列关系不正确的是( ).
A. B. C. D.,
第3题 第5题
4.(2019?牡丹江)将抛物线y=(x﹣1)2+3向左平移1个单位,得到的抛物线与y轴的交点坐标是( ).
A.(0,2) B.(0,3) C.(0,4) D.(0,7)
5.如图所示,抛物线的顶点坐标是P(1,3),则函数y随自变量x的增大而减小的x的取值范围是( ).
A. B. C. D.
6.若二次函数.当≤l时,随的增大而减小,则的取值范围是( )
A.=l B.>l C.≥l D.≤l
二、填空题
7.(2019?巴中模拟)抛物线y=x2+2x+7的开口向 ,对称轴是 ,顶点是 .
8.若点A(3,-4)在函数的图象上,则_ _.这个抛物线的对称轴是 ;
点A关于抛物线对称轴的对称点是 .
9.如果把抛物线向上平移-3个单位,再向右平移3个单位长度后得到抛物线,则求的值为 ;的值为 .
10.请写出一个二次函数,图象顶点为(-1,2),且不论x取何值,函数值y恒为正数.则此二次函数为______ __.
11.若二次函数中的x取值为2≤x≤5,则该函数的最大值为 ;最小值为 .
12.已知抛物线y=x2+x+b2经过点,则y1的值是_____.
三、解答题
13.抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,求△AOB的面积和周长.
14.(2019秋?湘西州期末)已知二次函数y=﹣x2+2(m﹣1)x+2m﹣m2的图象关于y轴对称,其顶点为A,与x轴两交点为B、C.
(1)求B、C两点的坐标.
(2)求△ABC的面积.
15.如图,在正方形ABCD中,AB=2,E是AD边上一点(点E与点A,D不重合).BE的垂直平分线交AB于M,交DC于N.
(1)设AE=x,四边形ADNM的面积为S,写出S关于x的函数关系式;
(2)当AE为何值时,四边形ADNM的面积最大?最大值是多少?
【答案与解析】
一、选择题 1.【答案】B;
【解析】抛物线y=a(x+m)2+m(a≠0)的顶点为(-m,m),所以顶点在直线y=-x上.
2.【答案】B;
【解析】当时,二次函数有最小值为2.
3.【答案】B;
【解析】由两抛物线对称轴相同可知,且由图象知,,.
4.【答案】B;
【解析】抛物线y=(x﹣1)2+3的顶点坐标为(1,3),
把点(1,3)向左平移1个单位得到点的坐标为(0,3),
所以平移后抛物线解析式为y=x2+3,
所以得到的抛物线与y轴的交点坐标为(0,3).
故选:B.
5.【答案】C;
【解析】由顶点坐标P(1,3)知抛物线的对称轴为直线,因此当时,y随x的增大而减小.
6.【答案】C;
【解析】画出草图进行分析得出结论.
二、填空题
7.【答案】上,x=﹣1,(﹣1,6).
【解析】∵y=x2+2x+7,
而a=1>0,
∴开口方向向上,
∵y=y=x2+2x+7=(x2+2x+1)+6=(x+1)2+6,
∴对称轴是x=﹣1,顶点坐标是(﹣1,6).
8.【答案】5或1; 直线x=5或直线x=1; 或(-1,-4);
【解析】因为点A(3,-4)在函数的图象上,所以把点A(3,-4)代入
函数得或;对称轴是直线x=5或直线x=1;点A关于抛物线对称轴的对称点是或(-1,-4).
9.【答案】 ,;
【解析】抛物线向上平移-3个单位得到,再向右平移3个单位长度得到,即与相同,故,.
10.【答案】 等;
【解析】答案不唯一,只要抛物线开口向上即可,即,所以或等均可.
11.【答案】50;5.
【解析】由于函数的顶点坐标为(1,2),,
当时,y随x的增大而增大,
当x=5时,函数在2≤x≤5范围内的最大值为50;
当x=2时,函数的最小值为.
12.【答案】;
【解析】把代入y=x2+x+b2得,,
,代入即可求得.
三、解答题
13.【答案与解析】
∵ 抛物线y=3(x-2)2与x轴交于点A,与y轴交于点B,
∴ A(2,0),B(0,12),
∴ S△AOB=12,△AOB的周长为14十.
14.【答案与解析】
解:由二次函数y=﹣x2+2(m﹣1)x+2m﹣m2的图象关于y轴对称,得
m﹣1=0.
解得m=1.
函数解析式为y=﹣x2+1,
当y=0时,﹣x2+1=0.
解得x1=﹣1,x2=1,
即B(﹣1,0),C(1,0);
(2)当x=0时,y=1,即A(0,1),
S△ABC=×2×1=1.
15.【答案与解析】
(1)连接ME,设MN交BE交于P,
根据题意得MB=ME,MN⊥BE.
过N作NF⊥AB于F,在Rt△MBP和Rt△MNF中,∠MBP+∠BMN=90°,
∠FNM+∠BMN=90°,∠MBP=∠MNF,又AB=FN,Rt△EBA≌Rt△MNF,MF=AE=x.
在Rt△AME中,由勾股定理得
ME2=AE2+AM2,
所以MB2=x2+AM2,即(2-AM)2=x2+AM2,解得AM=1-x2.
所以四边形ADNM的面积
S=×2=AM+AM+MF=2AM+AE=2(1-x2)+x=-x2+x+2.
即所求关系式为S=-x2+x+2.
(2)S=-x2+x+2=-(x2-2x+1)+=-(x-1)2+.
当AE=x=1时,四边形ADNM的面积S的值最大,此时最大值是.
