北师大版九年级上册数学第一讲特殊平行四边形(学案)
文档属性
| 名称 | 北师大版九年级上册数学第一讲特殊平行四边形(学案) |

|
|
| 格式 | zip | ||
| 文件大小 | 495.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-21 00:00:00 | ||
图片预览


文档简介
特殊的平四边形
适用学科 初中数学 适用年级 初中三年级
适用区域 全国 课时时长(分钟) 120分钟
知识点 1四边形以及特殊四边形的概念、性质、判定 三角形、梯形中位线定理及其运用 梯形、等腰梯形、直角梯形的概念,掌握等腰梯形的性质和判定,运用相关知识进行证明和计算
学习目标 掌握平行四边形及几种特殊四边形的性质与判定 灵活运用有关性质及判定解决问题 经历四边形基本性质,使学生学会“合乎逻辑地思考”,建立知识体系,获得一定的技能基础 4.让学生理解平面几何观念的基本途径是多种多样的,感知和体验几何图形的现实意义,体验二维空间相互转换关系
学习重点 理解和掌握几种常见特殊四边形的性质、判定
学习难点 发展合情推理和初步的演绎推理能力
学习过程
复习预习
上节课我们复习了勾股定理的内容,接下来请同学们回忆一下
1.勾股定理:
直角三角形两直角边a,b的平方和等于斜边c的平方,即.
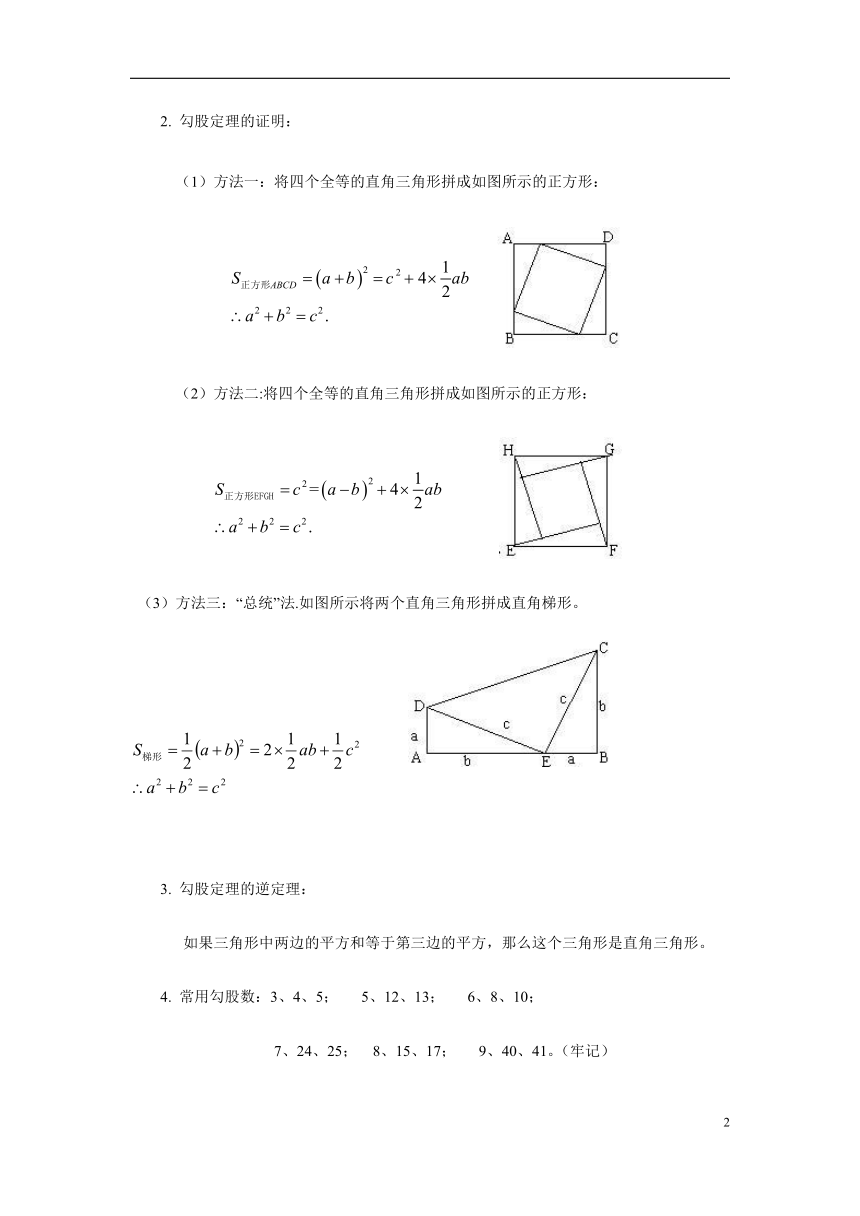
勾股定理的证明:
(1)方法一:将四个全等的直角三角形拼成如图所示的正方形:
(2)方法二:将四个全等的直角三角形拼成如图所示的正方形:
(3)方法三:“总统”法.如图所示将两个直角三角形拼成直角梯形。
3. 勾股定理的逆定理:
如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
4. 常用勾股数:3、4、5; 5、12、13; 6、8、10;
7、24、25; 8、15、17; 9、40、41。(牢记)
勾股数扩大相同倍数后,仍为勾股数.
知识讲解
1、平行四边形性质及判定,列表归纳
平行四边形 矩形 菱形 正方形
性 质 边 对边平行且相等 对边平行且相等 对边平行,四边相等 对边平行,四边相等
角 对角相等 四个角都是直角 对角相等 四个角都是直角
对角线 互相平分 互相平分且相等 互相垂直平分,且每条对角线平分一组对角 垂直平分且相等,每条对角线平分一组对角
判定 1.两组对边分别平行; 2.两组对边分别相等; 3.一组对边平行且相等; 4.两组对角分别相等; 5.两条对角线互相平分. 1有三个角是直角的四边形; 2有一个角是直角的平行四边形; 3对角线相等的平行四边形. 1.四边相等的四边形; 2.对角线互相垂直的平行四边形; 3.有一组邻边相等的平行四边形。 4.每条对角线平分一组对角的四边形。 1.有一个角是直角的菱形; 2.对角线相等的菱形; 3有一组邻边相等的矩形; 4.对角线互相垂直的矩形;
对 称性 只是中心对称图形 既是轴对称图形,又是中心对称图形
面积 S=(a为边,h为a上的高) S= S=(对角线积) S=
2.直角梯形定义:有一个角是直角的梯形叫做直角梯形。
等腰梯形定义:两腰相等的梯形叫做等腰梯形。
等腰梯形是轴对称图形,只有一条对称轴,一底的垂直平分线是它的对称轴。
3.中位线
三角形中位线定义:连接三角形两边中点的线段叫做三角形的中位线。(有三条)
三角形中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半。
梯形中位线定义:连接梯形两腰中点的线段,叫做梯形的中位线。(有且只有一条)
梯形中位线性质:梯形中位线平行于两底,并且等于两底和的一半。
4.平行线之间的距离及特征
平行线之间的距离定义:若两条直线互相平行,则其中一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离。
平行线之间的距离特征1:平行线之间的距离处处相等。
平行线之间的距离特征2:夹在两条平行线之间的平行线段相等。
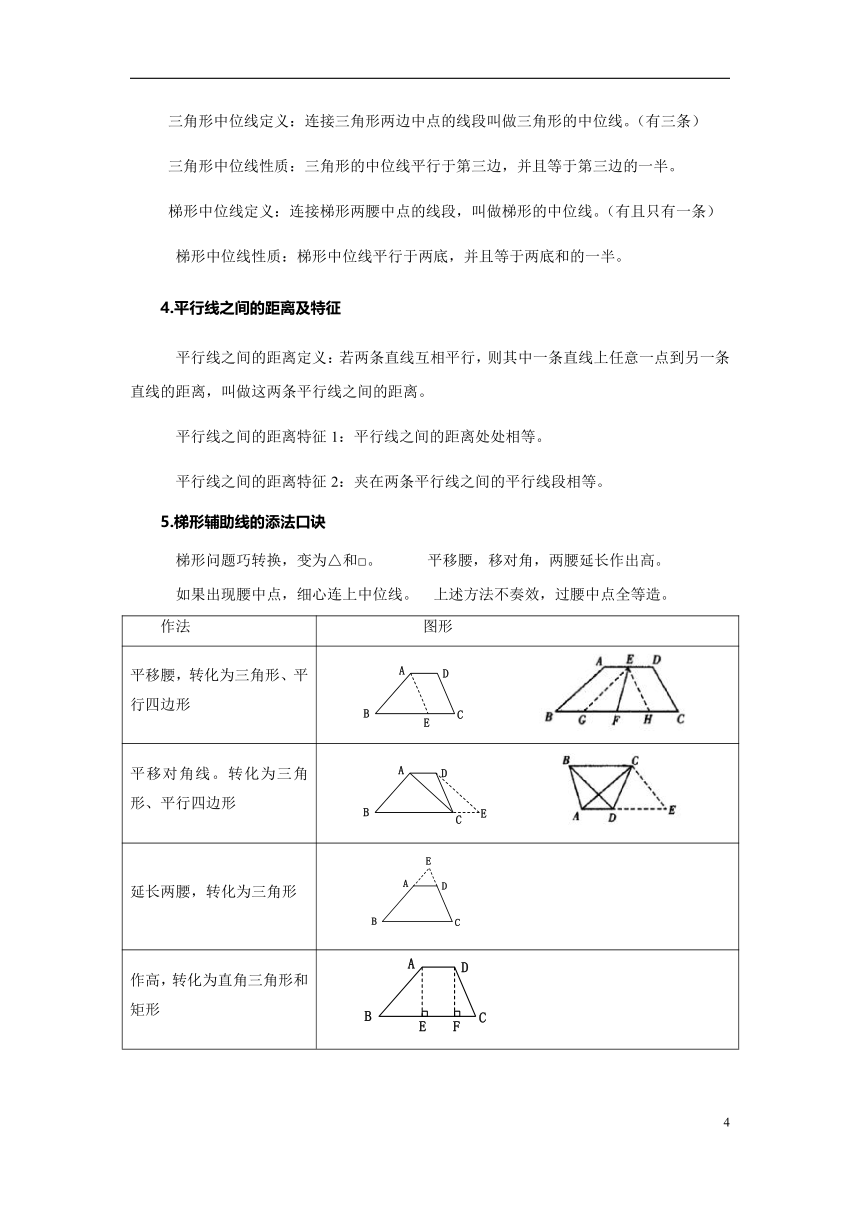
5.梯形辅助线的添法口诀
梯形问题巧转换,变为△和□。 平移腰,移对角,两腰延长作出高。
如果出现腰中点,细心连上中位线。 上述方法不奏效,过腰中点全等造。
作法 图形
平移腰,转化为三角形、平行四边形
平移对角线。转化为三角形、平行四边形
延长两腰,转化为三角形
作高,转化为直角三角形和矩形
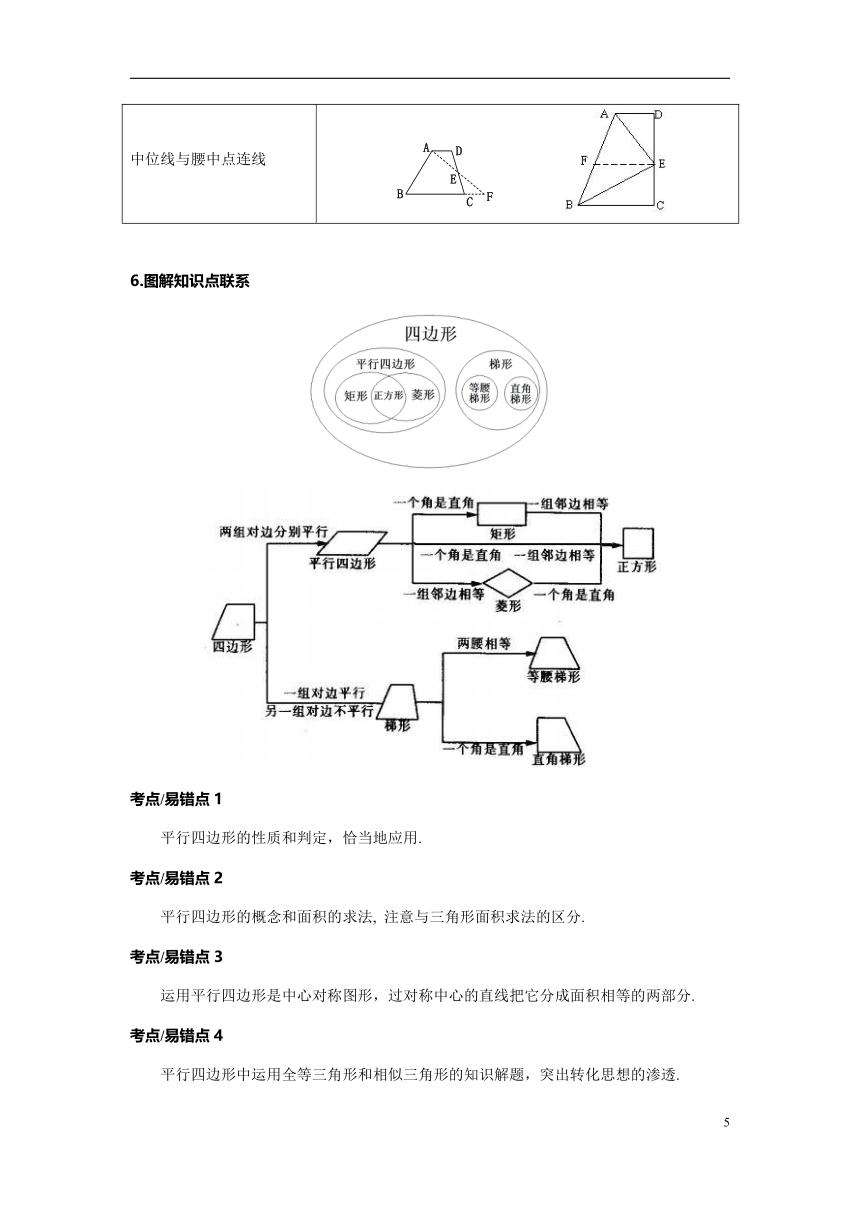
中位线与腰中点连线
6.图解知识点联系
考点/易错点1
平行四边形的性质和判定,恰当地应用.
考点/易错点2
平行四边形的概念和面积的求法, 注意与三角形面积求法的区分.
考点/易错点3
运用平行四边形是中心对称图形,过对称中心的直线把它分成面积相等的两部分.
考点/易错点4
平行四边形中运用全等三角形和相似三角形的知识解题,突出转化思想的渗透.
考点/易错点5
矩形、菱形、正方形的概念、性质、判定及它们之间的关系,主要考查边长、对角线长、面积等的计算
考点/易错点6
四边形中的翻折、平移、旋转、剪拼等动手操作性问题.
三、例题精析
【例题1】
【题干】下列说法中,正确的是( )
A.同位角相等 B.对角线相等的四边形是平行四边形
C.四条边相等的四边形是菱形 D.矩形的对角线一定互相垂直
【答案】C
解:A、如果两直线平行,同位角才相等,故本选项错误;
B、对角线互相平分的四边形是平行四边形,故本选项错误;
C、四边相等的四边形是菱形,故本选项正确;
D、矩形的对角线互相平分且相等,不一定垂直,故本选项错误;
【解析】根据平行线的性质判断A即可;根据平行四边形的判定判断B即可;根据菱形的判定判断C即可;根据矩形的性质判断D即可.
【例题2】
【题干】如图,四边形ABCD的对角线AC、BD相交于点O,且BD平分AC,若BD=8,AC=6,∠BOC=120°,则四边形ABCD的面积为 .(结果保留根号)
【答案】
【解析】BD平分AC,所以OA=OC=3,
因为∠BOC=120°,所以∠DOC=∠A0B=60°,
过C作CH⊥BD于H,过A作AG⊥BD于G,在△CHO中,∠C0H=60°,OC=3,
所以CH=,
同理:AG=,
所以四边形ABCD的面积=。
【例题3】
【题干】如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC是,连接BM、DN,若四边形MBND是菱形,则等于 ( )
A. B. C. D.
【答案】C
【解析】矩形的性质应用较为常见的就是转化成直角三角形来解决问题,菱形的性质应用较常见的是四条边相等或者对角线的性质应用。此题中求的是线段的比值,所以在解决过程中取特殊值法较为简单。设AB=1,则AD=2,因为四边形MBND是菱形,所以MB=MD,又因为矩形ABCD,所以A=90°,设AM=x,则MB=2-x,由勾股定理得:AB2+AM2=MB2,所以x2+12=(2-x)2解得:,所以MD=,
【例题4】
【题干】如图,在△ABC中,AC=BC,点D、E分别是边AB、AC的中点,将△ADE绕点E旋转180°得△CFE,则四边形ADCF一定是( )
A. 矩形 B. 菱形 C. 正方形 D. 梯形
【答案】A
解:∵△ADE绕点E旋转180°得△CFE,
∴AE=CE,DE=EF,
∴四边形ADCF是平行四边形,
∵AC=BC,点D是边AB的中点,
∴∠ADC=90°,
∴四边形ADCF矩形.
【解析】根据旋转的性质可得AE=CE,DE=EF,再根据对角线互相平分的四边形是平行四边形判断出四边形ADCF是平行四边形,然后利用等腰三角形三线合一的性质求出∠ADC=90°,再利用有一个角是直角的平行四边形是矩形解答.
【例题5】
【题干】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,
∠EFB=60°,则矩形ABCD的面积是 ( )
A.12 B. 24 C. 12 D. 16
【答案】D
【解析】由两直线平行内错角相等,知∠DEF=∠EFB=60°,又∠AEF=∠EF=120°,所以,∠E=60°,E=AE=2,求得,所以,AB=2,矩形ABCD的面积为S=2×8=16,选D。
【例题6】
【题干】如图,在?ABCD中,对角线AC与BD相交于点O,过点O作EF⊥AC交BC于点E,交AD于点F,连接AE、CF.则四边形AECF是( )
A. 梯形 B. 矩形 C. 菱形 D. 正方形
【答案】C
四边形AECF是菱形,
∵在?ABCD中,对角线AC与BD相交于点O,
∴AO=CO,∠AFO=∠CEO,
∴在△AFO和△CEO中
,
∴△AFO≌△CEO(AAS),
∴FO=EO,
∴四边形AECF平行四边形,
∵EF⊥AC,
∴平行四边形AECF是菱形.
【解析】首先利用平行四边形的性质得出AO=CO,∠AFO=∠CEO,进而得出△AFO≌△CEO,再利用平行四边形和菱形的判定得出即可.
【例题7】
【题干】如图菱形ABCD中,∠B=60°,AB=4,则以AC为边长的正方形ACEF的周长为( )
A.14 B.15 C.16 D.17
【答案】C
解:∵四边形ABCD是菱形,
∴AB=BC,
∵∠B=60°,
∴△ABC是等边三角形,
∴AC=AB=4,
∴正方形ACEF的周长是AC+CE+EF+AF=4×4=16,
【解析】根据菱形得出AB=BC,得出等边三角形ABC,求出AC长,根据正方形的性质得出AF=EF=EC=AC=4,求出即可.本题考查了菱形性质,正方形性质,等边三角形的性质和判定的应用,关键是求出AC的长.
【例题8】
【题干】如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是( )
A. 48 B. 60 C. 76 D. 80
【答案】C
解:∵∠AEB=90°,AE=6,BE=8,
∴在Rt△ABE中,AB2=AE2+BE2=100,
∴S阴影部分=S正方形ABCD﹣S△ABE=AB2﹣×AE×BE
=100﹣×6×8
=76.
【解析】由已知得△ABE为直角三角形,用勾股定理求正方形的边长AB,
用S阴影部分=S正方形ABCD﹣S△ABE求面积.
【例题9】
【题干】如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有( )个.
A. 2 B. 3 C. 4 D. 5
【答案】C
解:∵四边形ABCD是正方形,
∴AB=BC=CD=AD,∠B=∠BCD=∠D=∠BAD=90°.
∵△AEF等边三角形,
∴AE=EF=AF,∠EAF=60°.
∴∠BAE+∠DAF=30°.
在Rt△ABE和Rt△ADF中,
,
Rt△ABE≌Rt△ADF(HL),
∴BE=DF,①正确.
∠BAE=∠DAF,
∴∠DAF+∠DAF=30°,
即∠DAF=15°②正确,
∵BC=CD,
∴BC﹣BE=CD﹣DF,
即CE=CF,
∵AE=AF,
∴AC垂直平分EF.③正确.
设EC=x,由勾股定理,得
EF=x,CG=x,AG=x,
∴AC=,
∴AB=,
∴BE=﹣x=,
∴BE+DF=x﹣x≠x,④错误,
∵S△CEF=,
S△ABE==,
∴2S△ABE==S△CEF,⑤正确.
综上所述,正确的有4个,故选C.
【解析】通过条件可以得出△ABE≌△ADF而得出∠BAE=∠DAF,BE=DF,由正方形的性质就可以得出EC=FC,就可以得出AC垂直平分EF,设EC=x,由勾股定理就可以表示出BE与EF,利用三角形的面积公式分别表示出S△CEF和2S△ABE再通过比较大小就可以得出结论.
【例题10】
【题干】如图小亮用六块形状、大小完全相同的等腰梯形拼成一个四边形,则图中 HYPERLINK "http://www.7caiedu.cn/" 的度数是( )
A.60° B.55°
C.50° D.45°
【答案】A
【解析】本题考查等腰梯形的性质及镶嵌知识.以三个等腰梯形形成镶嵌的某个顶点处分析,三个相等的底角和为360度,所以每个上底角等于120度,下底角为60度.
【例题11】
【题干】已知:菱形ABCD中,对角线AC与BD相交于点O,OE∥DC交BC于点E,AD=6cm,则OE的长为( )
A.6 cm B.4 cm C.3 cm D.2 cm
【答案】C
【解析】本题考查菱形的有关性质及相似三角形的判定及应用.解题关键:线段OE的一个端点O为对角线的中点,要求OE长,只需证明OE是中位线.菱形ABCD中,AD=CD=6,因为OE∥DC,所以△BEO∽△BCD,所以BO︰BD=OE︰CD,又因为O是BD中点,所以 HYPERLINK "http://www.7caiedu.cn/" 。
【例题12】
【题干】如图,在梯形ABCD中,AD//BC,AB=DC,AC与BD相交于点P。已知A(2, 3),
B(1, 1),D(4, 3),则点P的坐标为( , )。
【答案】 (3, )
【解析】如图,由对称性可知P的横坐标为3,
,即,所以,PE=,+1=
故P的坐标为(3,)。
四、课堂运用
【基础】
1.矩形具有而菱形不具有的性质是( )
A.两组对边分别平行 B.对角线相等
C.对角线互相平分 D.两组对角分别相等
2.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若矩形ABCD和矩形AEFC的面积分别是S1、S2的大小关系是( )
A. S1>S2 B. S1=S2 C. S1<S2 D. 3S1=2S2
3.如图,菱形ABCD的两条对角线相交于O,若AC=6,BD=4,则菱形ABCD的周长是( )
A. 24 B. 16 C. 4 D. 2
4. 如图,把一个长方形的纸片对折两次,然后剪下一个角,为了得到一个钝角为120° 的菱形,剪口与第二次折痕所成角的度数应为( )
A.15°或30° B.30°或45° C.45°或60° D.30°或60°
5. 如图,边长为6的大正方形中有两个小正方形,若两个小正方形的面积分别为S1,S2,则S1+S2的值为( )
A.16 B.17 C.18 D.19
【巩固】
1.如图,在矩形ABCD中,AB<BC,AC,BD相交于点O,则图中等腰三角形的个数是( )
A. 8 B. 6 C. 4 D. 2
2.已知:线段AB,BC,∠ABC = 90°. 求作:矩形ABCD.
以下是甲、乙两同学的作业:对于两人的作业,下列说法正确的是( )
A.两人都对 B.两人都不对
C.甲对,乙不对 D.甲不对,乙对
3. 如图,在给定的一张平行四边形纸片上作一个菱形.甲、乙两人的作法如下:
甲:连接AC,作AC的垂直平分线MN分别交AD,AC,BC于M,O,N,连接AN,CM,则四边形ANCM是菱形.
乙:分别作∠A,∠B的平分线AE,BF,分别交BC,AD于E,F,连接EF,则四边形ABEF是菱形.
根据两人的作法可判断( )
A. 甲正确,乙错误 B. 乙正确,甲错误 C. 甲、乙均正确 D. 甲、乙均错误
4. 如图,四边形ABCD、AEFG均为正方形,其中E在BC上,且B、E两点不重合,并连接BG.根据图中标示的角判断下列∠1、∠2、∠3、∠4的大小关系何者正确?( )
A.∠1<∠2 B.∠1>∠2 C.∠3<∠4 D.∠3>∠4
如图为正三角形ABC与正方形DEFG的重迭情形,其中D、E两点分别在AB、BC上,且BD=BE.若AC=18,GF=6,则F点到AC的距离为何?( )
A.2 B.3 C.12﹣4 D.6﹣6
【拔高】
1.如图,在矩形ABCD中,点E是边CD的中点,将△ADE沿AE折叠后得到△AFE,且点F在矩形ABCD内部.将AF延长交边BC于点G.若=,则= 用含k的代数式表示).
2.已知,在△ABC中,∠BAC=90°,∠ABC=45°,点D为直线BC上一动点(点D不与点B,C重合).以AD为边做正方形ADEF,连接CF
(1)如图1,当点D在线段BC上时.求证CF+CD=BC;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CF,BC,CD三条线段之间的关系;
(3)如图3,当点D在线段BC的反向延长线上时,且点A,F分别在直线BC的两侧,其他条件不变;
①请直接写出CF,BC,CD三条线段之间的关系;
②若正方形ADEF的边长为2,对角线AE,DF相交于点O,连接OC.求OC的长度.
课程小结
准确掌握平行四边形、矩形、菱形、正方形、等腰梯形的概念、性质和判定,这些都是应考的重要前提。
中位线定理
梯形辅助线添加方法
用转化思想求解数形结合题、方案设计题,以及一些综合题。
课后作业
【基础】
1. 如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则△AEF的周长= cm.
2. 如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2,BC=2,则图中阴影部分的面积为 .
【巩固】
将矩形ABCD绕点A顺时针旋转到矩形A’B’C’D’的位置,旋转角为 (0<<90)。若1=110,则= 。
如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件 ____________,使ABCD成为菱形.(只需添加一个即可)
3.如图,菱形ABCD中,AB=4,,,垂足分别为E,F,连接EF,则△AEF的面积是 .
4. 如图,将菱形纸片ABCD折迭,使点A恰好落在菱形的对称中心O处,折痕为EF。若菱形ABCD的边长为2 cm, A=120,则EF= cm。
若菱形的两条对角线分别为2和3,则此菱形的面积是 .
【拔高】
1.如图,正方形ABCD的边长为3,点E,F分别在边AB,BC上,AE=BF=1,小球P从点E出发沿直线向点F运动,每当碰到正方形的边时反弹,反弹时反射角等于入射角.当小球P第一次碰到点E时,小球P与正方形的边碰撞的次数为 ,小球P所经过的路程为 .
2. 如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .
3. 如图,在正方形ABCD中,E是AB上一点,F是AD延长线上一点,且DF=BE.
(1)求证:CE=CF;
(2)若点G在AD上,且∠GCE=45°,则GE=BE+GD成立吗?为什么?
错题总结
错题题号 错题比例 错题原因 错题知识点小结
课堂运用
课后作业
B
C
D
A
M
N
x
y
A
B
C
D
P
O
A
B
C
D
B’
1
C’
D’
1
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
