2019年秋北师大版八年级数学上册7.5三角形内角和定理作业设计含答案
文档属性
| 名称 | 2019年秋北师大版八年级数学上册7.5三角形内角和定理作业设计含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 158.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-21 00:00:00 | ||
图片预览


文档简介
5 三角形内角和定理
一、选择题
1. 在△ABC中,∠A=75°,∠B-∠C=15°,则∠C的度数为( )
A. 30° B. 45° C. 50° D. 10°
2. 在△ABC中,如果∠A=∠B=4∠C,那么∠C的度数是( )
A. 10° B. 20° C. 30° D. 40°
3. 下列说法错误的是( )
A. 一个三角形中至少有一个角不大于60° B. 锐角三角形中任意两个角的和小于直角
C. 一个三角形中至多有一个角是钝角 D. 一个三角形中至多有一个角是直角
4. 下列叙述中正确的是( )
A. 三角形的外角等于两个内角的和 B. 三角形的外角大于内角
C. 三角形的外角等于与它不相邻的两个内角和 D. 三角形每一个内角都只有一个外角
5. 如果三角形三个外角的度数比为2∶3∶4,则与之对应的三个内角的度数比为( )
A. 4∶3∶2 B. 3∶2∶4 C. 5∶3∶1 D. 3∶1∶5
6. 三角形的一个外角,不大于和它相邻的内角,这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 非锐角三角形
7. 等腰三角形的一个外角为110°,它的底角为( )
A. 55° B. 70° C. 55°或70° D. 以上答案都不对
8. 在△ABC中,∠A=36°,∠C是直角,则∠B=________.
9. 在△ABC中
(1)∠A∶∠B∶∠C=1∶1∶2,则此三角形是______ 三角形;
(2)∠A∶∠B∶∠C=2∶3∶5,则此三角形是______ 三角形;
(3)∠A=2∠B=3∠C,则此三角形是______ 三角形;
(4)∠A=∠B=∠C,则此三角形是______ 三角形;
(5)∠A-∠B=∠C,则此三角形是______ 三角形.
10. 如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,则∠DBC=_______.
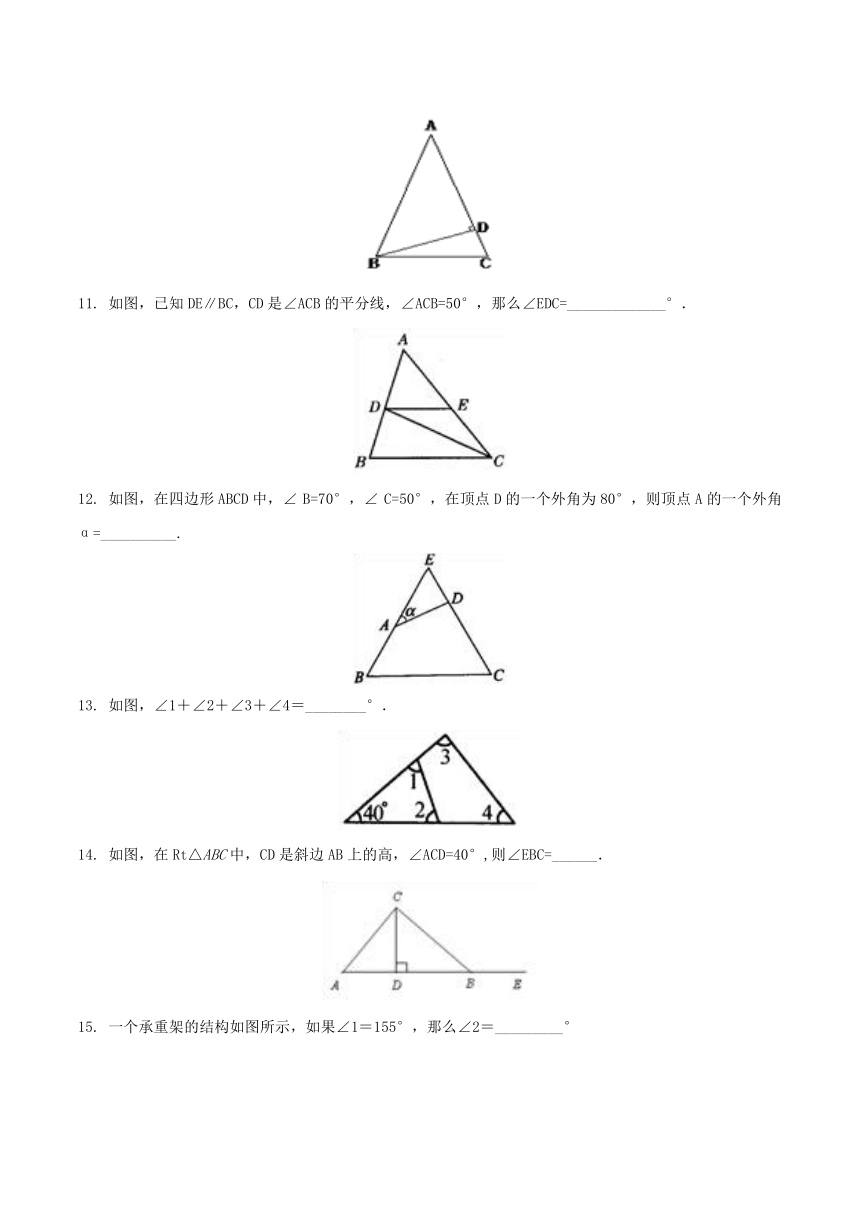
11. 如图,已知DE∥BC,CD是∠ACB的平分线,∠ACB=50°,那么∠EDC=_____________°.
12. 如图,在四边形ABCD中,∠ B=70°,∠ C=50°,在顶点D的一个外角为80°,则顶点A的一个外角α=__________.
13. 如图,∠1+∠2+∠3+∠4=________°.
14. 如图,在Rt△ABC中,CD是斜边AB上的高,∠ACD=40°,则∠EBC=______.
15. 一个承重架的结构如图所示,如果∠1=155°,那么∠2=_________°
16. 已知∠ABC,∠ACB的平分线交于I.
(1)根据下列条件分别求出∠BIC的度数:
①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°.
(2)你能发现∠BIC与∠A的关系吗?
17. 如图,在△ABC中,D,E分别是BC,AC上的点,AD,BE相交于F,求证:∠C+∠1+∠2+∠3=180°.
答案
一、选择题
1. 【答案】B
【解析】∵∠A+∠B+∠C=180o(三角形内角和为180 o),且∠A=75°,∠B=50°,∴∠C=180o-(∠A+∠B)
=180 o-(75°+50°)=55°,故选D.
2. 【答案】B
【解析】设∠C =k°,则三个内角的度数分别为4k°,4k°,k°,根据三角形内角和定理,可知4k°+4k°+k°=180°,得k°=20°,即∠C的度数是20°.故选B.
3. 【答案】B
【解析】如果锐角三角形中任意两个角的和小于直角,那么不符合三角形内角和定理.故选B.
4. 【答案】C
【解析】A、三角形的外角等于和它不相邻的两个内角的和,故本选项错误;B、三角形的外角大于和它不相邻的一个内角,故本选项错误.C、符合三角形外角的性质,故本选项正确;D、三角形每一个内角都有两个外角,故本选项错误.故选C.
5. 【答案】C
【解析】∵三角形三个外角的度数之比为2:3:4,而这三个外角的和为360°,∴这三个外角分别为:
80°、120°、160°,∴与这三个外角相邻的内角度数分别为:100°、60°、20°,∴对应的三个内角的度数之比为:100:60:20=5:3:1.故选C.
6. 【答案】D
【解析】因为三角形的一个外角与它相邻的内角和为180°,而题中说这个外角大于它相邻的内角,所以可知与它相邻的这个内角是一个大于或等于90°的角,则这个三角形就是一个钝角三角形或直角三角形.故选D.
7. 【答案】C
【解析】因为等腰三角形的一个外角为110°,所以相邻的内角为180°-110°=70°,分两种情况讨论:(1)当此角是底角时,则它的底角为70°;(2)当此角为顶角时,则底角为(180°-70°)÷2=55°∴综上可知,底角为55°和70°.故选C.
考点:1.等腰三角形的性质;2.三角形内角和定理;3.三角形的外角性质.
8.【答案】54°
【解析】根据直角三角形的两个锐角互余得:∠B=90°-∠A=90°-36°=54°.
9. 【答案】 (1). 等腰直角; (2). 直角; (3). 钝角; (4). 直角; (5). 直角;
【解析】(1)∠A:∠B:∠C=1:1:2,则∠A=∠B,且∠C=90°.则此三角形是等腰直角三角形;(2)∠A:∠B:∠C=2:3:5,设∠A=2x.则2x+3x+5x=180°,解得x=18°.则5x=5×18=90°,则此三角形是直角三角形;(3)∠A=2∠B=3∠C,同(2)求解,解得∠A>90°,则此三角形是钝角三角形;(4)∠A=
∠B=∠C,同(2)求解,解得∠C=90°,则此三角形是直角三角形;(5)∠A-∠B=∠C,同(2)求解,解得∠A=90°,则此三角形是直角三角形.
10.【答案】18°
【解析】设∠A=x,则∠C=∠ABC=2x.根据三角形内为180°知,∠C+∠ABC+∠A=180°,即2x+2x+x=180°,
所以x=36°,∠C=2x=72°.在直角三角形BDC中,∠DBC=90°-∠C=90°-72°=18°.
考点:三角形内角和定理.
11.【答案】25
【解析】∵DE∥BC,∴∠EDC=∠DCB,∵CD是∠ACB的平分线,∴∠ECD=∠DCB,∴∠EDC=∠ECD,
∵∠ACB=50°,∴∠EDC=∠ECD=25°.
12.【答案】40°
【解析】如图,∵∠B=70°,∠C=50°,∴∠E=180°-∠B-∠C=180°-70°-50°=60°,∴∠α=180°-60°-100°=20°.
13.【答案】280
【解析】根据三角形内角和定理,可得:∠1+∠2=180°-40°=140°,∠3+∠4=180°-40°=140°,则∠1+∠2
+∠3+∠4=140°+140°=280°.故答案为:280.
14. 【答案】140°
【解析】∵在Rt△ABC中,CD是斜边AB上的高,∴∠ABC=∠ACD=90°﹣∠BCD=40°,∴∠EBC=180°﹣∠ABC=140°.故答案为:140.
15.【答案】65
【解析】根据三角形的一个外角等于和它不相邻的两个内角的和解答.∵∠1=155°,∠2+90°=∠1,∴∠2=155°-90°=65°.
16.【答案】(1)①∠BIC=120°;②∠BIC=120°;③∠BIC=135°;④∠BIC=90°+n°.
(2)∠BIC=90°+∠A.
【解析】(1)①已知∠ABC,∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;②已知∠ABC+∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;③已知∠A,由内角和定理求∠ABC+
∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;④已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;(2)∠BIC的大小不发生变化.可由角平分线的性质及三角形内角和定理求出∠BIC=90°+∠A.
解:(1)①∵在△ABC中,∠ABC=70°,∠ACB=50°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC=35°,∠ICB=∠ACB=25°,
∴∠BIC=180°-∠IBC-∠ICB=120°;
②∵在△ABC中,∠ABC+∠ACB=120°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=120°;
③∵∠A=90°,∴∠ABC+∠ACB=90°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=135°;
④∵∠A=n°,∴∠ABC+∠ACB=180°-n°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=90°+n°;
(2)∠BIC的大小不发生变化.
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=180°-(∠ABC+∠ACB),=180°-(180°-∠A),=90°+∠A,
17.【答案】证明见解析.
【解析】根据三角形外角的性质推出∠2=∠FAB+∠FBA,根据三角形内角和定理,即可推出∠C+∠1+∠2+
∠3=∠C+∠1+∠FAB+∠FBA+∠3=∠C+∠CAB+∠ABC=180°.
证明:∵∠ADB是△ADC的外角
∴∠ADB=∠3+∠C
∵∠1+∠2+∠ADB=180°
∴∠1+∠2+∠3+∠C=180°
PAGE
一、选择题
1. 在△ABC中,∠A=75°,∠B-∠C=15°,则∠C的度数为( )
A. 30° B. 45° C. 50° D. 10°
2. 在△ABC中,如果∠A=∠B=4∠C,那么∠C的度数是( )
A. 10° B. 20° C. 30° D. 40°
3. 下列说法错误的是( )
A. 一个三角形中至少有一个角不大于60° B. 锐角三角形中任意两个角的和小于直角
C. 一个三角形中至多有一个角是钝角 D. 一个三角形中至多有一个角是直角
4. 下列叙述中正确的是( )
A. 三角形的外角等于两个内角的和 B. 三角形的外角大于内角
C. 三角形的外角等于与它不相邻的两个内角和 D. 三角形每一个内角都只有一个外角
5. 如果三角形三个外角的度数比为2∶3∶4,则与之对应的三个内角的度数比为( )
A. 4∶3∶2 B. 3∶2∶4 C. 5∶3∶1 D. 3∶1∶5
6. 三角形的一个外角,不大于和它相邻的内角,这个三角形一定是( )
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 非锐角三角形
7. 等腰三角形的一个外角为110°,它的底角为( )
A. 55° B. 70° C. 55°或70° D. 以上答案都不对
8. 在△ABC中,∠A=36°,∠C是直角,则∠B=________.
9. 在△ABC中
(1)∠A∶∠B∶∠C=1∶1∶2,则此三角形是______ 三角形;
(2)∠A∶∠B∶∠C=2∶3∶5,则此三角形是______ 三角形;
(3)∠A=2∠B=3∠C,则此三角形是______ 三角形;
(4)∠A=∠B=∠C,则此三角形是______ 三角形;
(5)∠A-∠B=∠C,则此三角形是______ 三角形.
10. 如图,在△ABC中,∠C=∠ABC=2∠A,BD是AC边上的高,则∠DBC=_______.
11. 如图,已知DE∥BC,CD是∠ACB的平分线,∠ACB=50°,那么∠EDC=_____________°.
12. 如图,在四边形ABCD中,∠ B=70°,∠ C=50°,在顶点D的一个外角为80°,则顶点A的一个外角α=__________.
13. 如图,∠1+∠2+∠3+∠4=________°.
14. 如图,在Rt△ABC中,CD是斜边AB上的高,∠ACD=40°,则∠EBC=______.
15. 一个承重架的结构如图所示,如果∠1=155°,那么∠2=_________°
16. 已知∠ABC,∠ACB的平分线交于I.
(1)根据下列条件分别求出∠BIC的度数:
①∠ABC=70°,∠ACB=50°;②∠ACB+∠ABC=120°;③∠A=90°;④∠A=n°.
(2)你能发现∠BIC与∠A的关系吗?
17. 如图,在△ABC中,D,E分别是BC,AC上的点,AD,BE相交于F,求证:∠C+∠1+∠2+∠3=180°.
答案
一、选择题
1. 【答案】B
【解析】∵∠A+∠B+∠C=180o(三角形内角和为180 o),且∠A=75°,∠B=50°,∴∠C=180o-(∠A+∠B)
=180 o-(75°+50°)=55°,故选D.
2. 【答案】B
【解析】设∠C =k°,则三个内角的度数分别为4k°,4k°,k°,根据三角形内角和定理,可知4k°+4k°+k°=180°,得k°=20°,即∠C的度数是20°.故选B.
3. 【答案】B
【解析】如果锐角三角形中任意两个角的和小于直角,那么不符合三角形内角和定理.故选B.
4. 【答案】C
【解析】A、三角形的外角等于和它不相邻的两个内角的和,故本选项错误;B、三角形的外角大于和它不相邻的一个内角,故本选项错误.C、符合三角形外角的性质,故本选项正确;D、三角形每一个内角都有两个外角,故本选项错误.故选C.
5. 【答案】C
【解析】∵三角形三个外角的度数之比为2:3:4,而这三个外角的和为360°,∴这三个外角分别为:
80°、120°、160°,∴与这三个外角相邻的内角度数分别为:100°、60°、20°,∴对应的三个内角的度数之比为:100:60:20=5:3:1.故选C.
6. 【答案】D
【解析】因为三角形的一个外角与它相邻的内角和为180°,而题中说这个外角大于它相邻的内角,所以可知与它相邻的这个内角是一个大于或等于90°的角,则这个三角形就是一个钝角三角形或直角三角形.故选D.
7. 【答案】C
【解析】因为等腰三角形的一个外角为110°,所以相邻的内角为180°-110°=70°,分两种情况讨论:(1)当此角是底角时,则它的底角为70°;(2)当此角为顶角时,则底角为(180°-70°)÷2=55°∴综上可知,底角为55°和70°.故选C.
考点:1.等腰三角形的性质;2.三角形内角和定理;3.三角形的外角性质.
8.【答案】54°
【解析】根据直角三角形的两个锐角互余得:∠B=90°-∠A=90°-36°=54°.
9. 【答案】 (1). 等腰直角; (2). 直角; (3). 钝角; (4). 直角; (5). 直角;
【解析】(1)∠A:∠B:∠C=1:1:2,则∠A=∠B,且∠C=90°.则此三角形是等腰直角三角形;(2)∠A:∠B:∠C=2:3:5,设∠A=2x.则2x+3x+5x=180°,解得x=18°.则5x=5×18=90°,则此三角形是直角三角形;(3)∠A=2∠B=3∠C,同(2)求解,解得∠A>90°,则此三角形是钝角三角形;(4)∠A=
∠B=∠C,同(2)求解,解得∠C=90°,则此三角形是直角三角形;(5)∠A-∠B=∠C,同(2)求解,解得∠A=90°,则此三角形是直角三角形.
10.【答案】18°
【解析】设∠A=x,则∠C=∠ABC=2x.根据三角形内为180°知,∠C+∠ABC+∠A=180°,即2x+2x+x=180°,
所以x=36°,∠C=2x=72°.在直角三角形BDC中,∠DBC=90°-∠C=90°-72°=18°.
考点:三角形内角和定理.
11.【答案】25
【解析】∵DE∥BC,∴∠EDC=∠DCB,∵CD是∠ACB的平分线,∴∠ECD=∠DCB,∴∠EDC=∠ECD,
∵∠ACB=50°,∴∠EDC=∠ECD=25°.
12.【答案】40°
【解析】如图,∵∠B=70°,∠C=50°,∴∠E=180°-∠B-∠C=180°-70°-50°=60°,∴∠α=180°-60°-100°=20°.
13.【答案】280
【解析】根据三角形内角和定理,可得:∠1+∠2=180°-40°=140°,∠3+∠4=180°-40°=140°,则∠1+∠2
+∠3+∠4=140°+140°=280°.故答案为:280.
14. 【答案】140°
【解析】∵在Rt△ABC中,CD是斜边AB上的高,∴∠ABC=∠ACD=90°﹣∠BCD=40°,∴∠EBC=180°﹣∠ABC=140°.故答案为:140.
15.【答案】65
【解析】根据三角形的一个外角等于和它不相邻的两个内角的和解答.∵∠1=155°,∠2+90°=∠1,∴∠2=155°-90°=65°.
16.【答案】(1)①∠BIC=120°;②∠BIC=120°;③∠BIC=135°;④∠BIC=90°+n°.
(2)∠BIC=90°+∠A.
【解析】(1)①已知∠ABC,∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;②已知∠ABC+∠ACB,由内角和定理求∠BAC,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;③已知∠A,由内角和定理求∠ABC+
∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;④已知∠A,由内角和定理求∠ABC+∠ACB,再根据角平分线性质求∠IBC+∠ICB,在△IBC中,由内角和定理求∠BIC的度数;(2)∠BIC的大小不发生变化.可由角平分线的性质及三角形内角和定理求出∠BIC=90°+∠A.
解:(1)①∵在△ABC中,∠ABC=70°,∠ACB=50°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC=35°,∠ICB=∠ACB=25°,
∴∠BIC=180°-∠IBC-∠ICB=120°;
②∵在△ABC中,∠ABC+∠ACB=120°,
∴∠BAC=180°-∠ABC-∠ACB=60°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=120°;
③∵∠A=90°,∴∠ABC+∠ACB=90°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=135°;
④∵∠A=n°,∴∠ABC+∠ACB=180°-n°,
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=90°+n°;
(2)∠BIC的大小不发生变化.
∵BD、CE分别是∠ABC、∠ACB的平分线,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠BIC=180°-∠IBC-∠ICB=180°-(∠ABC+∠ACB),=180°-(180°-∠A),=90°+∠A,
17.【答案】证明见解析.
【解析】根据三角形外角的性质推出∠2=∠FAB+∠FBA,根据三角形内角和定理,即可推出∠C+∠1+∠2+
∠3=∠C+∠1+∠FAB+∠FBA+∠3=∠C+∠CAB+∠ABC=180°.
证明:∵∠ADB是△ADC的外角
∴∠ADB=∠3+∠C
∵∠1+∠2+∠ADB=180°
∴∠1+∠2+∠3+∠C=180°
PAGE
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
