安徽省安庆市太湖县白沙中学2018-2019学年度第一学期沪科版九年级数学上第一次月考试卷(九月第21、22章含答案)
文档属性
| 名称 | 安徽省安庆市太湖县白沙中学2018-2019学年度第一学期沪科版九年级数学上第一次月考试卷(九月第21、22章含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 130.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 21:45:30 | ||
图片预览



文档简介
安徽省安庆市太湖县白沙中学2018-2019学年度第一学期沪科版
九年级数学上第一次月考试卷(九月 第21、22章)
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若函数是关于的二次函数,则的值是( )
A. B. C.或 D.任何实数
?2.已知变量和成反比例,当时,,那么当时,的值是( )
A. B. C. D.
?3.龙游已连续年列中国最具投资潜力中小城市百强,位次由年的位上升到年的第位,而龙游的荣昌广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式为( )
A. B.
C. D.
?4.函数的图象与直线没有交点,那么的取值范围是( )
A. B. C. D.
?5.下列函数中是二次函数的是( )
A. B.
C. D.
?6.已知关于的方程,若为正实数,则下列判断正确的是( )
A.有三个不等实数根 B.有两个不等实数根
C.有一个实数根 D.无实数根
?7.已知关于的二次函数在上的函数值始终是正的,则的取值范围( )
A. B.或
C. D.
?8.若矩形的面积为,矩形的长为,宽为,则关于的函数图象大致是( )
A. B.
C. D.
?9.已知二次函数的与的部分对应值如下表:则下列判断中正确的是
… …
… …
A.抛物线开口向上 B.抛物线与轴交于负半轴
C.当时, D.方程的正根在与之间
?10.已知二次函数的图象,关于的方程的根的情况是( )
A.无实根 B.有两相等的实根
C.有两不相等且同号的实根 D.有两不等且异号的实根
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.函数,当取________值时,它为二次函数.
?12.如图,二次函数和一次函数的图象,观察图象,写出时的取值范围________.
?13.已知,则________.
?14.大矩形的周长是与它位似的小矩形的倍,小矩形的面积是,大矩形的长为,则大矩形的宽为________.
?
15.已知线段,,则________.
?16.某商店经营一种水产品,成本为每千克元的水产品,据市场分析,若按每千克元销售,一个月能售出千克,销售价每涨元,月销售量就减少千克,针对这种水产品的销售情况,销售单价定为________元时,获得的利润最多.
?17.在平面直角坐标系中,点、、的坐标分别为、、.如果是围成的区域(含边界)上的点,那么当取得最大值时,点的坐标是________.
?
18.已知函数是反比例函数,且图象在第二、四象限内,则的值是________.
?19.如图,正方形的边长为,点是边上不与点、重合的任意一点,连接,过点作
交于点,设的长为,的长为.
点在上运动的过程中的最大值为________;
当时,求的值为________.
20.如图,双曲线与直线相交于、两点,为此双曲线在第一象限内的任一点(在点左侧),设直线、分别与轴相交于、两点,且,,则的值为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,正方形中顶点在一双曲线上,请在图中画出一条过点的直线,使之与双曲线的另一支交于点,且满足线段最短.
?
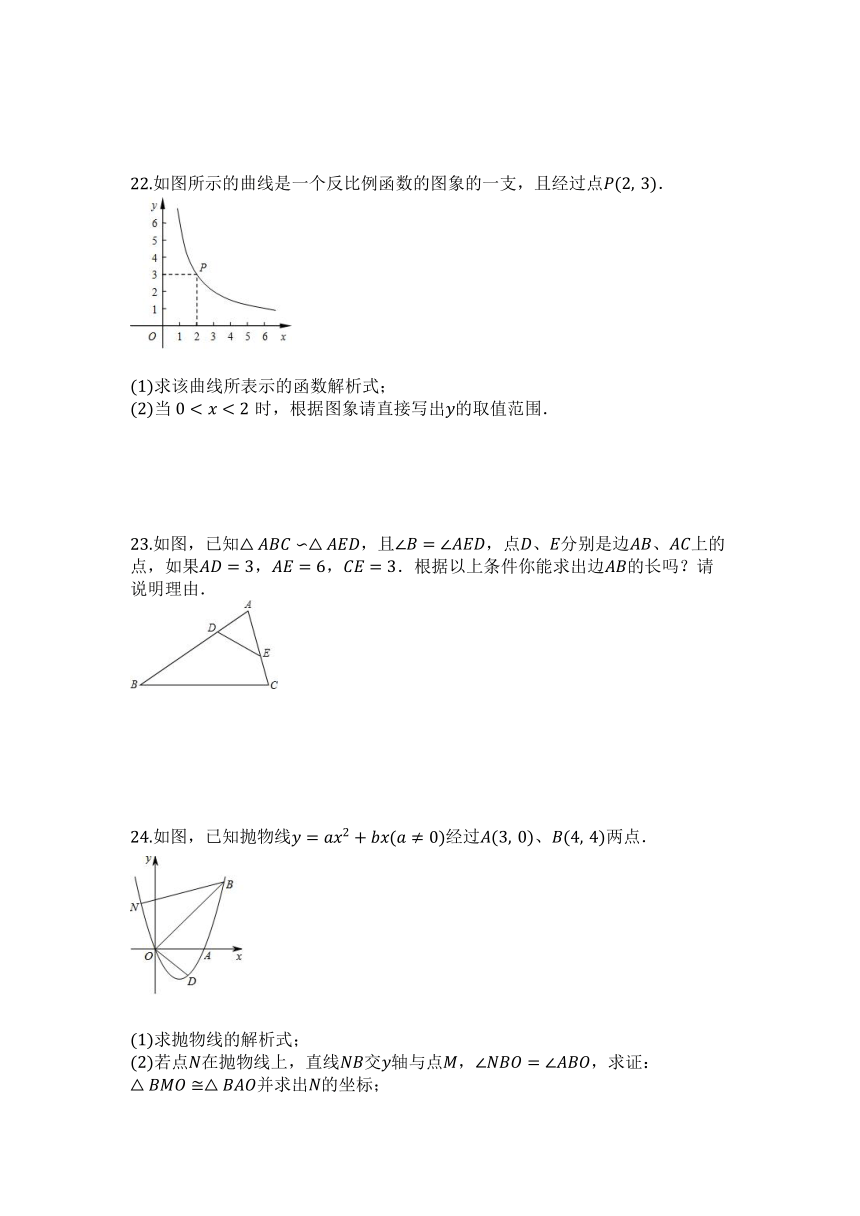
22.如图所示的曲线是一个反比例函数的图象的一支,且经过点.
求该曲线所表示的函数解析式;
当时,根据图象请直接写出的取值范围.
?
23.如图,已知,且,点、分别是边、上的点,如果,,.根据以上条件你能求出边的长吗?请说明理由.
?
24.如图,已知抛物线经过、两点.
求抛物线的解析式;
若点在抛物线上,直线交轴与点,,求证:并求出的坐标;
在的条件下,已知点,在坐标平面内有一点,使(点、、分别与点、、对应),求点坐标.
?
25.如图,已知、、三点在同一条直线上,与都是等边三角形,其中线段交于点,线段交于点.求证:.
?
26.如图,在平面直角坐标系中,梯形的边在轴的正半轴上,,,过点的双曲线的一支在第一象限交梯形对角线于点,交边于点.
填空:双曲线的另一支在第________象限,的取值范围是________;
若点的坐标为,请用含有的式子表示阴影部分的面积.并回答:当点在什么位置时,阴影部分面积最小?
若,,求双曲线的解析式.
答案
1.B
2.B
3.D
4.B
5.D
6.C
7.A
8.D
9.D
10.D
11.
12.或
13.
14.
15.
16.
17.
18.
19.解:∵,度.
又∵,
∴,
∴,
因此,点在上运动时始终有,
∵,,,
∴,
∴,
∵,
∴随的增大而减小,有最大值(当时),最大;由知,当时,,
整理,得,
∵,
∴.
∵,
∴当时,的值是或.
20.
21.解:∵双曲线关于直线及直线对称,而线段在直线上,则易得
∴最短.
22.解:设反比例函数解析式为,
∵图象经过,
∴,
∴反比例函数解析式为;由反比例函数图象可直接看出当时,.
23.解:∵,且,
∴.
又,,,
∴.
24.解:∵抛物线经过、,
∴把、两点坐标代入可得,
解得,
∴抛物线的解析式是.∵直线的解析式为,且,
根据轴对称性质得出,
在和中
∴,
∴,
∴点,
∴可设直线的解析式为,过点,代入可得,解得,
∴直线的解析式是,
∵点在直线上,
∴设点,
又点在抛物线上,
∴,解得:,(不合题意,舍去),
∴点的坐标为;如图,将沿轴翻折,得到,则,
∵,,
∴、、都在直线上.
∵,,
∴,
∴,
∴点的坐标为;
将沿直线翻折,由对称性可得另一个满足条件的点,
综上所述,点的坐标是或.
25.证明:∵与都是等边三角形,
∴,,,
∴,
∴,
∴,
同理,,
∴.
26.三∵梯形的边在轴的正半轴上,,,
∵点的坐标为,
∴点的纵坐标为,点的横坐标为,点坐标为,
把代入得;把代入得,
∴点的坐标为,点的坐标为,
∴
,
,
,
当,即时,最小,最小值为;
∴点的坐标为,即点为的中点,
∴当点在的中点时,阴影部分的面积最小;设点坐标为,
∵,
∴,即点为的中点,
∴点坐标为,
∴点的纵坐标为,
把代入得,
∴点坐标为,
∵,
∴,
∴,
∴双曲线的解析式为
九年级数学上第一次月考试卷(九月 第21、22章)
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.若函数是关于的二次函数,则的值是( )
A. B. C.或 D.任何实数
?2.已知变量和成反比例,当时,,那么当时,的值是( )
A. B. C. D.
?3.龙游已连续年列中国最具投资潜力中小城市百强,位次由年的位上升到年的第位,而龙游的荣昌广场中心标志性建筑处有高低不同的各种喷泉,其中一支高度为米的喷水管喷水的最大高度为米,此时喷水水平距离为米,在如图所示的坐标系中,这支喷泉的函数关系式为( )
A. B.
C. D.
?4.函数的图象与直线没有交点,那么的取值范围是( )
A. B. C. D.
?5.下列函数中是二次函数的是( )
A. B.
C. D.
?6.已知关于的方程,若为正实数,则下列判断正确的是( )
A.有三个不等实数根 B.有两个不等实数根
C.有一个实数根 D.无实数根
?7.已知关于的二次函数在上的函数值始终是正的,则的取值范围( )
A. B.或
C. D.
?8.若矩形的面积为,矩形的长为,宽为,则关于的函数图象大致是( )
A. B.
C. D.
?9.已知二次函数的与的部分对应值如下表:则下列判断中正确的是
… …
… …
A.抛物线开口向上 B.抛物线与轴交于负半轴
C.当时, D.方程的正根在与之间
?10.已知二次函数的图象,关于的方程的根的情况是( )
A.无实根 B.有两相等的实根
C.有两不相等且同号的实根 D.有两不等且异号的实根
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.函数,当取________值时,它为二次函数.
?12.如图,二次函数和一次函数的图象,观察图象,写出时的取值范围________.
?13.已知,则________.
?14.大矩形的周长是与它位似的小矩形的倍,小矩形的面积是,大矩形的长为,则大矩形的宽为________.
?
15.已知线段,,则________.
?16.某商店经营一种水产品,成本为每千克元的水产品,据市场分析,若按每千克元销售,一个月能售出千克,销售价每涨元,月销售量就减少千克,针对这种水产品的销售情况,销售单价定为________元时,获得的利润最多.
?17.在平面直角坐标系中,点、、的坐标分别为、、.如果是围成的区域(含边界)上的点,那么当取得最大值时,点的坐标是________.
?
18.已知函数是反比例函数,且图象在第二、四象限内,则的值是________.
?19.如图,正方形的边长为,点是边上不与点、重合的任意一点,连接,过点作
交于点,设的长为,的长为.
点在上运动的过程中的最大值为________;
当时,求的值为________.
20.如图,双曲线与直线相交于、两点,为此双曲线在第一象限内的任一点(在点左侧),设直线、分别与轴相交于、两点,且,,则的值为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,正方形中顶点在一双曲线上,请在图中画出一条过点的直线,使之与双曲线的另一支交于点,且满足线段最短.
?
22.如图所示的曲线是一个反比例函数的图象的一支,且经过点.
求该曲线所表示的函数解析式;
当时,根据图象请直接写出的取值范围.
?
23.如图,已知,且,点、分别是边、上的点,如果,,.根据以上条件你能求出边的长吗?请说明理由.
?
24.如图,已知抛物线经过、两点.
求抛物线的解析式;
若点在抛物线上,直线交轴与点,,求证:并求出的坐标;
在的条件下,已知点,在坐标平面内有一点,使(点、、分别与点、、对应),求点坐标.
?
25.如图,已知、、三点在同一条直线上,与都是等边三角形,其中线段交于点,线段交于点.求证:.
?
26.如图,在平面直角坐标系中,梯形的边在轴的正半轴上,,,过点的双曲线的一支在第一象限交梯形对角线于点,交边于点.
填空:双曲线的另一支在第________象限,的取值范围是________;
若点的坐标为,请用含有的式子表示阴影部分的面积.并回答:当点在什么位置时,阴影部分面积最小?
若,,求双曲线的解析式.
答案
1.B
2.B
3.D
4.B
5.D
6.C
7.A
8.D
9.D
10.D
11.
12.或
13.
14.
15.
16.
17.
18.
19.解:∵,度.
又∵,
∴,
∴,
因此,点在上运动时始终有,
∵,,,
∴,
∴,
∵,
∴随的增大而减小,有最大值(当时),最大;由知,当时,,
整理,得,
∵,
∴.
∵,
∴当时,的值是或.
20.
21.解:∵双曲线关于直线及直线对称,而线段在直线上,则易得
∴最短.
22.解:设反比例函数解析式为,
∵图象经过,
∴,
∴反比例函数解析式为;由反比例函数图象可直接看出当时,.
23.解:∵,且,
∴.
又,,,
∴.
24.解:∵抛物线经过、,
∴把、两点坐标代入可得,
解得,
∴抛物线的解析式是.∵直线的解析式为,且,
根据轴对称性质得出,
在和中
∴,
∴,
∴点,
∴可设直线的解析式为,过点,代入可得,解得,
∴直线的解析式是,
∵点在直线上,
∴设点,
又点在抛物线上,
∴,解得:,(不合题意,舍去),
∴点的坐标为;如图,将沿轴翻折,得到,则,
∵,,
∴、、都在直线上.
∵,,
∴,
∴,
∴点的坐标为;
将沿直线翻折,由对称性可得另一个满足条件的点,
综上所述,点的坐标是或.
25.证明:∵与都是等边三角形,
∴,,,
∴,
∴,
∴,
同理,,
∴.
26.三∵梯形的边在轴的正半轴上,,,
∵点的坐标为,
∴点的纵坐标为,点的横坐标为,点坐标为,
把代入得;把代入得,
∴点的坐标为,点的坐标为,
∴
,
,
,
当,即时,最小,最小值为;
∴点的坐标为,即点为的中点,
∴当点在的中点时,阴影部分的面积最小;设点坐标为,
∵,
∴,即点为的中点,
∴点坐标为,
∴点的纵坐标为,
把代入得,
∴点坐标为,
∵,
∴,
∴,
∴双曲线的解析式为
同课章节目录
