湖南省娄底市双峰县青树坪中学2018-2019学年度第一学期湘教版九年级数学上册_第一章反比例函数单元检测试卷(含答案)
文档属性
| 名称 | 湖南省娄底市双峰县青树坪中学2018-2019学年度第一学期湘教版九年级数学上册_第一章反比例函数单元检测试卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 142.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-20 21:57:57 | ||
图片预览



文档简介
湖南省娄底市双峰县青树坪中学2018-2019学年度第一学期湘教版
九年级数学上册 第一章 反比例函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.某反比例函数的图象经过点,则此函数的图象也经过点( )
A. B.
C. D.
?2.如图,反比例函数的图象经过点.则当时,函数值的取值范围是( )
A. B.
C. D.
?3.若与成反比例,且当时,,则与之间的函数关系式是( )
A. B.
C. D.
?4.已知,是反比例函数的图象上的三点,且,则,的大小关系是( )
A. B. C. D.无法判断
?5.若正比例函数与反比例函数的图象交于点,且点的横坐标是,则此反比例函数的解析式为( )
A. B.
C. D.
?6.如图,点是反比例函数图象上一点,轴,垂足为点,,则以下结论:
①常数;②在每个象限内,随的增大而减小;③当时,的取值范围是;④若点在图象上,则点也在图象上.其中正确的是( )
A.①② B.③④ C.②④ D.①③
?7.点是反比例函数上的一点,且,是方程的根,则反比例函数的解析式是( )
A. B. C. D.
?8.己知如图,反比例函数或各一支,若轴,与图象分别交于、两点,若的面积为,则下列说法正确的是( )
A. B.
C. D.
?9.根据欧姆定律,当电压一定时,电流与电阻的函数图象大致是( )
A. B.
C. D.
?10.如图,矩形在第一象限,在轴正半轴上,,,直线经过点交轴于点,双曲线经过点,则双曲线与边的交点坐标是( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知反比例函数的图象经过点,则当时,________.
?12.函数的图象上两点和,且,分别过,向轴作轴于,轴于,则________,若,则函数解析式为________.
?13.若点在反比例函数的图象上,则当函数值时,自变量的取值范围是________.
?
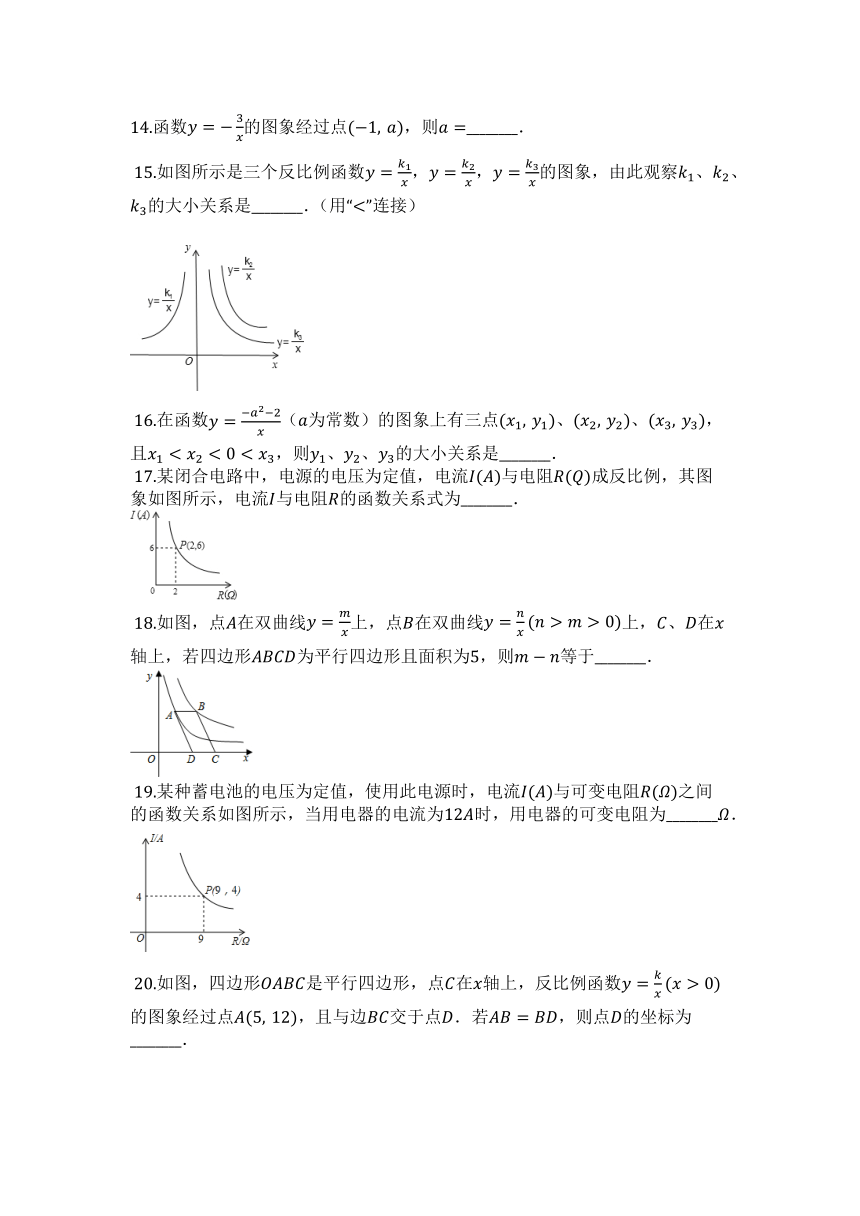
14.函数的图象经过点,则________.
?15.如图所示是三个反比例函数,,的图象,由此观察、、的大小关系是________.(用“”连接)
?16.在函数(为常数)的图象上有三点、、,且,则、、的大小关系是________.
?17.某闭合电路中,电源的电压为定值,电流与电阻成反比例,其图象如图所示,电流与电阻的函数关系式为________.
?18.如图,点在双曲线上,点在双曲线上,、在轴上,若四边形为平行四边形且面积为,则等于________.
?19.某种蓄电池的电压为定值,使用此电源时,电流与可变电阻之间的函数关系如图所示,当用电器的电流为时,用电器的可变电阻为________.
?20.如图,四边形是平行四边形,点在轴上,反比例函数的图象经过点,且与边交于点.若,则点的坐标为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,反比例函数的图象与一次函数的图象交于,两点.
求反比例函数与一次函数的解析式;
求的面积;
根据图象回答:当取何值时,一次函数的函数值大于反比例函数的函数值.(直接写出结论)
?
22.如图,已知双曲线与直线.
若它们在第二象限有公共点,求双曲线及直线的解析式;
试说明点是它们的唯一公共点;
若将直线进行上下平移,使它与双曲线没有公共点,请直接写出的取值范围.
?
23.如图,在平面直角坐标系中,反比例函数与正比例函数的图象相交于、两点,点的纵坐标为.
求正比例函数的表达式及点的坐标;
结合图象直接写出当时,的取值范围是________.
?
24.已知如图,反比例函数的图象上有一点,■,它的纵坐标被墨水污染了,根据题意,解答下列问题.
求出点的坐标;
过作垂直于轴,垂足为,求的面积.
?
25.若反比例函数与一次函数的图象都经过点
求一次函数的解析式;
画出直线,两个函数图象的另一个交点为,求点的坐标;
求的面积.
?
26.为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比,燃烧后,与成反比(如图所示),现测得药物分钟燃烧完,此时教室内每立方米空气含
药量为.根据以上信息解答下列问题:
求药物燃烧时以及药物燃烧后与的函数关系式;
当每立方米空气中含药量低于时对人体无害,那么从消毒开始经多长时间后学生才能进教室?
当每立方米空气中药物含量不低于且持续时间不低于分钟时消毒才有效,那么这次消毒效果如何?
答案
1.B
2.D
3.D
4.B
5.D
6.C
7.C
8.D
9.B
10.B
11.
12.
13.或
14.
15.
16.
17.
18.
19.
20.
21.解:∵反比例函数过,
∴,即,
∴此反比例函数的解析式为:;
∵反比例函数过,
∴,解得;
∵一次函数的图象交于两点,.
∴,解得
∴一次函数的解析式为:;
∵直线的解析式为,
∴,
∴,
∵,,
∴.∵,,
由函数图象可知,当或时一次函数的图象在反比例函数图象的上方,
∴当或时一次函数的值大于反比例函数的值;
22.解:把代入得:,
则反比例函数的解析式是;
把代入得:,
解得:,
则函数的解析式是:;根据题意得:,
去分母,整理得:,
,则方程有两个相同的解,
则直线和反比例函数只有一个公共点,即点是它们的唯一公共点;当直线与反比例函数第四象限部分有一个公共点时,公共点一定是.
把代入直线的解析式得:,
解得:,
当直线经过点时:,
则将直线进行上下平移,使它与双曲线没有公共点,的取值范围是.
23.或.
24.解:∵当时,,
∴;∵,
∴.
25.解:已知反比例函数过点,则,
故的坐标为,
将其坐标代入一次函数的解析式,可得,
解可得,
故一次函数的解析式为;
根据题意,可得,
解可得,或
故交点设与轴交于点,
则的坐标为.
则,
故的面积是.
26.解:当时,即药物燃烧时,设与的函数关系式为:,
∴,
∴,
∴药物燃烧时与的函数关系式为;
当时,即设药物燃烧后与的函数关系式为,
∴,
∴,
∴药物燃烧后与的函数关系式为:;
∴药物燃烧时以及药物燃烧后与的函数关系式为:;当时,,
∴,
∴分钟后才能进教室.令,
∴,
∴,
∴,
∴.
∴,
∴此次消毒效果没有效.
九年级数学上册 第一章 反比例函数 单元检测试卷
考试总分: 120 分 考试时间: 120 分钟
学校:__________ 班级:__________ 姓名:__________ 考号:__________
一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?1.某反比例函数的图象经过点,则此函数的图象也经过点( )
A. B.
C. D.
?2.如图,反比例函数的图象经过点.则当时,函数值的取值范围是( )
A. B.
C. D.
?3.若与成反比例,且当时,,则与之间的函数关系式是( )
A. B.
C. D.
?4.已知,是反比例函数的图象上的三点,且,则,的大小关系是( )
A. B. C. D.无法判断
?5.若正比例函数与反比例函数的图象交于点,且点的横坐标是,则此反比例函数的解析式为( )
A. B.
C. D.
?6.如图,点是反比例函数图象上一点,轴,垂足为点,,则以下结论:
①常数;②在每个象限内,随的增大而减小;③当时,的取值范围是;④若点在图象上,则点也在图象上.其中正确的是( )
A.①② B.③④ C.②④ D.①③
?7.点是反比例函数上的一点,且,是方程的根,则反比例函数的解析式是( )
A. B. C. D.
?8.己知如图,反比例函数或各一支,若轴,与图象分别交于、两点,若的面积为,则下列说法正确的是( )
A. B.
C. D.
?9.根据欧姆定律,当电压一定时,电流与电阻的函数图象大致是( )
A. B.
C. D.
?10.如图,矩形在第一象限,在轴正半轴上,,,直线经过点交轴于点,双曲线经过点,则双曲线与边的交点坐标是( )
A. B. C. D.
二、填空题(共 10 小题 ,每小题 3 分 ,共 30 分 )
?11.已知反比例函数的图象经过点,则当时,________.
?12.函数的图象上两点和,且,分别过,向轴作轴于,轴于,则________,若,则函数解析式为________.
?13.若点在反比例函数的图象上,则当函数值时,自变量的取值范围是________.
?
14.函数的图象经过点,则________.
?15.如图所示是三个反比例函数,,的图象,由此观察、、的大小关系是________.(用“”连接)
?16.在函数(为常数)的图象上有三点、、,且,则、、的大小关系是________.
?17.某闭合电路中,电源的电压为定值,电流与电阻成反比例,其图象如图所示,电流与电阻的函数关系式为________.
?18.如图,点在双曲线上,点在双曲线上,、在轴上,若四边形为平行四边形且面积为,则等于________.
?19.某种蓄电池的电压为定值,使用此电源时,电流与可变电阻之间的函数关系如图所示,当用电器的电流为时,用电器的可变电阻为________.
?20.如图,四边形是平行四边形,点在轴上,反比例函数的图象经过点,且与边交于点.若,则点的坐标为________.
三、解答题(共 6 小题 ,每小题 10 分 ,共 60 分 )
?21.如图,反比例函数的图象与一次函数的图象交于,两点.
求反比例函数与一次函数的解析式;
求的面积;
根据图象回答:当取何值时,一次函数的函数值大于反比例函数的函数值.(直接写出结论)
?
22.如图,已知双曲线与直线.
若它们在第二象限有公共点,求双曲线及直线的解析式;
试说明点是它们的唯一公共点;
若将直线进行上下平移,使它与双曲线没有公共点,请直接写出的取值范围.
?
23.如图,在平面直角坐标系中,反比例函数与正比例函数的图象相交于、两点,点的纵坐标为.
求正比例函数的表达式及点的坐标;
结合图象直接写出当时,的取值范围是________.
?
24.已知如图,反比例函数的图象上有一点,■,它的纵坐标被墨水污染了,根据题意,解答下列问题.
求出点的坐标;
过作垂直于轴,垂足为,求的面积.
?
25.若反比例函数与一次函数的图象都经过点
求一次函数的解析式;
画出直线,两个函数图象的另一个交点为,求点的坐标;
求的面积.
?
26.为了预防流感,学校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量与燃烧时间(分钟)成正比,燃烧后,与成反比(如图所示),现测得药物分钟燃烧完,此时教室内每立方米空气含
药量为.根据以上信息解答下列问题:
求药物燃烧时以及药物燃烧后与的函数关系式;
当每立方米空气中含药量低于时对人体无害,那么从消毒开始经多长时间后学生才能进教室?
当每立方米空气中药物含量不低于且持续时间不低于分钟时消毒才有效,那么这次消毒效果如何?
答案
1.B
2.D
3.D
4.B
5.D
6.C
7.C
8.D
9.B
10.B
11.
12.
13.或
14.
15.
16.
17.
18.
19.
20.
21.解:∵反比例函数过,
∴,即,
∴此反比例函数的解析式为:;
∵反比例函数过,
∴,解得;
∵一次函数的图象交于两点,.
∴,解得
∴一次函数的解析式为:;
∵直线的解析式为,
∴,
∴,
∵,,
∴.∵,,
由函数图象可知,当或时一次函数的图象在反比例函数图象的上方,
∴当或时一次函数的值大于反比例函数的值;
22.解:把代入得:,
则反比例函数的解析式是;
把代入得:,
解得:,
则函数的解析式是:;根据题意得:,
去分母,整理得:,
,则方程有两个相同的解,
则直线和反比例函数只有一个公共点,即点是它们的唯一公共点;当直线与反比例函数第四象限部分有一个公共点时,公共点一定是.
把代入直线的解析式得:,
解得:,
当直线经过点时:,
则将直线进行上下平移,使它与双曲线没有公共点,的取值范围是.
23.或.
24.解:∵当时,,
∴;∵,
∴.
25.解:已知反比例函数过点,则,
故的坐标为,
将其坐标代入一次函数的解析式,可得,
解可得,
故一次函数的解析式为;
根据题意,可得,
解可得,或
故交点设与轴交于点,
则的坐标为.
则,
故的面积是.
26.解:当时,即药物燃烧时,设与的函数关系式为:,
∴,
∴,
∴药物燃烧时与的函数关系式为;
当时,即设药物燃烧后与的函数关系式为,
∴,
∴,
∴药物燃烧后与的函数关系式为:;
∴药物燃烧时以及药物燃烧后与的函数关系式为:;当时,,
∴,
∴分钟后才能进教室.令,
∴,
∴,
∴,
∴.
∴,
∴此次消毒效果没有效.
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
