第二章 整式的加减复习课件(70张PPT)
文档属性
| 名称 | 第二章 整式的加减复习课件(70张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-22 09:59:59 | ||
图片预览










文档简介
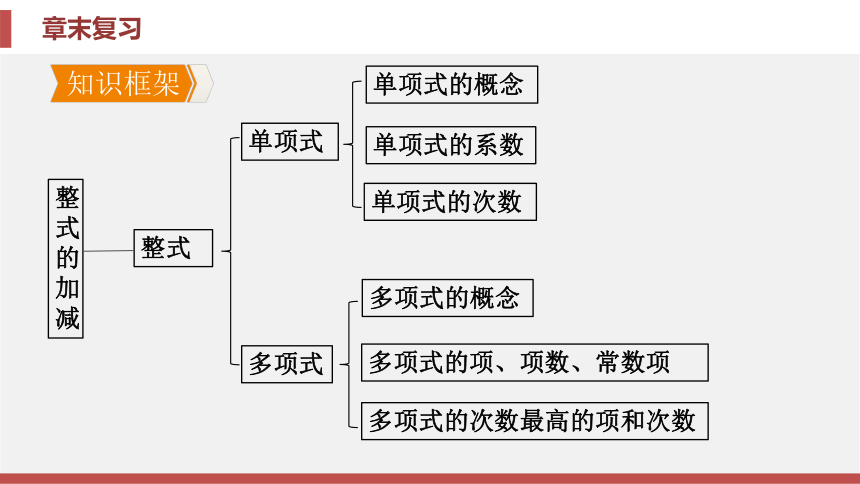
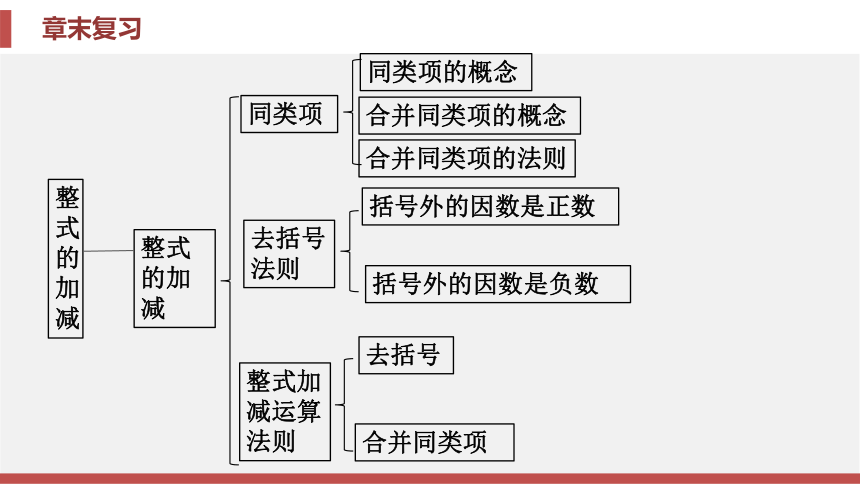
课件70张PPT。七年级 上册新课标(RJ)数 学 第二章 整式的加减章末复习第二章 整式的加减章末复习知识框架归纳整合素养提升中考链接知识框架整式的加减整式单项式多项式单项式的概念单项式的系数单项式的次数多项式的概念多项式的项、项数、常数项多项式的次数最高的项和次数整式的加减整式的加减同类项整式加减运算法则同类项的概念合并同类项的概念合并同类项的法则括号外的因数是正数括号外的因数是负数去括号去括号法则合并同类项【要点指导】根据实际问题列含字母的式子时, 首先明确问题中各 种量的属性以及关系, 例如分清不变的量与变化的量, 然后根据实际生活 中的数量关系(路程与速度的关系、商品售价与单价的关系、折扣问题 等), 列出含字母的式子, 同时注意带单位的含字母的式子的表示方式.归纳整合专题一 用字母表示数 A例1 随着服装市场竞争日益激烈, 某品牌服装专卖店一款服装按原售 价降价a元后, 再次降价20%, 现售价为b元, 则原售价为( ). B相关题1 (1)下列[厦门中考]某商店举办 促销活动, 促销的方法是 将原来x元的衣服以( - 10)元出售, 则下列说法中 能正确表述该商店促销方 法的是( ).
A. 原价减去10元后再打 8折 B. 原价打8折后再减去 10元 C. 原价减去10元后再打 2折 D. 原价打2折后再减去 10元【要点指导】本专题主要是对“三式”和“四数”的考查.“三式” 即单项式、多项式和整式, “四数”是指单项式的系数与次数、多项式 的项数与次数. 解决这类问题的关键是熟记概念, 利用概念解题.专题二 整式的有关概念例2 下列各式中, 哪些是单项式?哪些是多项式?并指出单项式及 多项式的次数. 相关题2 (1)将
填入相应的括号中. 单项式:{ …}; 多项式:{ …}; 整式:{ …}. 相关题2 (2)填表3a,-1-x,5x2,7-2x2y,6xy4,-3.1253a5x26xy4一次二项式二次三项式五次三项式相关题2 (3)已知 的次数为 10, 则2m+2n-1的值为 . 17例3 已知多项式
(1)写出多项式各项的系数和次数;
(2)若多项式的次数为8, 求a的值. 分析 多项式每一项的系数包括它前面的符号, 不可以漏掉. π是常数不 是字母, 所以本题多项式中的第一项的系数与π有关, 而次数与π无关.相关题3 多项式 是六次三项式, 则m , n .≠-5=5【要点指导】同类项指所含字母相同, 并且相同字母的指数也相同的 项. 常常根据同类项中相同字母的指数相同建立等量关系列出方程.专题三 同类项与合并同类项 例4 若 是同类项, 则m+n的值为( ).
A.1 B.2 C.3 D.4 C分析 由题意, 得m=1, n=2, 所以m+n=1+2=3. 相关题4 若 的和是单 项式, 求2a+b的值.
解:因为-xa+1y4与4ybx2的和是单项式,
所以-xa+1y4与4ybx2是同类项,
所以a+1=2,b=4,
解得a=1,b=4,
所以2a+b=2×1+4=6.专题四 整式的加减【要点指导】整式加减的实质是去括号、合并同类项, 在去括号时注 意符号问题.例5 一名同学做一道题: “已知两个多项式A和B, 计算2A+B.”他误 将“2A+B”看成“A+2B” , 求得的结果为9x2-2x+7. 已知B=x2+3x-2, 请求 出2A+B的正确结果. 解 由题意, 得A=9x2-2x+7-2(x2+3x-2)=9x2-2x+7-2x2-6x+4=7x2-8x+11.
所以2A+B=2(7x2-8x+11)+(x2+3x-2)=14x2-16x+22+x2+3x-2=15x213x+20. 相关题5 有一道题目:“当x=100时, 求整式(8-7x-6x2+ x3 )+ (x3 +5x2+4x-1)-(-x2-3x+2x3 -3)的值.” 甲同学 做题时把x=100错抄成 x=10, 乙同学没抄错, 但他们得出来的结果却一样, 你能说明原因吗?解:因为(8-7x-6x2+x3)+(x3+5x2+4x-1)-(-x2-3x+2x3-3)=8-7x-6x2+x3+x3+5x2+4x-1+x2+3x-2x3+3=10,与字母x的取值无关,所以,当x=100和x=10时的计算结果是一样的.专题五 整式的化简求值【要点指导】整式的化简求值通常是先把整式化简, 然后再代入求值. 整式的化简求值有以下三类:一是化简后直接代入求值;二是化简 后整体代入求值;三是先通过隐含条件将字母的值求出, 再代入求值.分析 (1)先去括号、合并同类项, 再代入求值;(2)先将条件变形, 然 后代入求值;(3)利用非负性求出a,b的值.例6 (1)先化简, 再求值:
其中x=-3, y=1;
(2)已知x2+3x+5的值为7, 求式子3x2+9x-2的值;
(3)已知(a-2)2+|b+1|=0, 求3a2b-[2a2b-(2ab-a2b)-4a2]-ab的值. 解 (1)原式= x-2x+y- x+3y=-3x+4y.
当x=-3, y=1时, 原式=-3×(-3)+4×1=13.
(2)因为x2+3x+5的值为7, 所以x2+3x=2,
所以3x2+9x-2=3(x2+3x)-2=3×2-2=4.
(3)因为(a-2)2≥0, |b+1|≥0, 且(a-2)2+|b+1|=0,
所以a-2=0, b+1=0, 解得a=2, b=-1.
所以3a2b-[2a2b-(2ab-a2b)-4a2]-ab
=3a2b-(2a2b-2ab+a2b-4a2)-ab
=3a2b-2a2b+2ab-a2b+4a2-ab
=4a2+ab =4×22+2×(-1) =14. 相关题6 (1)先化简, 再求值:
其中x=-1, y=2;
已知2a-3b2=5, 求10-2a+3b2的值.专题六 整式加减在实际生活中的应用【要点指导】整式加减的实际应用, 主要是对生活中的实际问题列 式计算, 解决问题的关键是审清题意, 用式子正确表示实际问题中的数量关系.例7 小明乘公共汽车到城里的书店买书, 小明上车后, 发现车上共 有(3a-b+1)人, 车到中途站时, 下去(2a-3)人, 但又上来若干人, 这时公共 汽车上共有(8a-5b)人, 则中途上车多少人?当a=5, b=6时, 中途上车多 少人? 分析 中途上车的乘客数=现有乘客数-原有乘客数+中途下车的乘 客数. 解:中途上车人数为(8a-5b) -(3a-b+1) +(2a-3)=8a-5b-3a+b1+2a-3=7a-4b-4. 当a=5, b=6时, 中途上车7a-4b-4=7×5-4×6-4=7(人). 相关题7 汛期来临前, 滨海区决定 实施“海堤加固”工程, 某 工程队承包了该项目, 计 划每天加固60米.在施工 前, 得到气象部门的预报,近期有台风袭击滨海区, 于 是工程队改变计划, 每天加 固的海堤长度是原计划的 1.5倍, 这样赶在台风来临 前完成加固任务.设滨海区 要加固的海堤长为a米, 则 完成整个任务的实际时间 比原计划少用了 天 (用含a的式子表示). 专题七 程序运算问题【要点指导】若是单一程序, 则可列出程序式求解;若程序有多 种模式, 则要根据输入的数据选择恰当的程序式求解;若程序中含有 “是”“否”, 则可逐步计算求解. 另外, 若已知输出结果求输入的数值, 应逆向思考, 但要注意, 程序中的每一步运算都要变为相应的逆运算.6例8 如图2-Z-1所示的运算程序中, 若开始输入的x值为48, 我们发 现第1次输出的结果为24, 第2次输出的结果为12……则第2019次输出的结 果为 .从表中可看出, 第3次输出的结果为6, 第4次输出的结果为3, 第5次输 出的结果为6, 第6次输出的结果为3, 第7次输出的结果为6, 第8次输出的结 果为3, 第9次输出的结果为6, 第10次输出的结果为3……即从第3次开始, 第奇数次输出的结果为偶数6, 第偶数次输出的结果为奇数3, 所以第2019 次输出的结果为6.相关题8 如图2-Z-2所示的运算程 序中, 若开始输入x=-1,则 最后输出的结果是 .-9专题八 月历中的学问【要点指导】月历中, 每行的数都是从小到大排列的, 后一个数比前 一个大1;每列中下一个数总比上一个大7;从右上方往左下方, 左下方 的数都比右上方的数大6;从左上方往右下方, 右下方的数都比左上方的 数大8.例9 假如老师在假期外出旅行一周, 这一周在同一个月, 你能帮老 师算一算, 这七天的日期之和与外出第四天的日期有什么关系吗?分析 设外出第四天的日期为x, 则其他各天的日期分别为x-1, x+1, x-2, x+2, x-3, x+3.解:这七天的日期之和为(x+1)+(x-1)+(x+2)+(x-2)+(x+3)+(x3)+x=7x, 所以可以发现这七天的日期之和是第四天的日期的7倍.相关题9 如图2-Z-3是某月的月历.
(1)带阴影的方框中的5个 数的和与方框正中心的数 有什么关系?
(2)如果将带阴影的方框移 动到其他位置, 还能得到上 述结论吗?用你所学的知 识说明理由.解: (1)2+9+16+8+10=45.方框中5个数的和是方框正中心的数的5倍.
(2)还能得到上面的结论.理由如下:
设正中间方框中的数为x,则其他的4个数分别为x+1,x-1,x+7,x-7.所以这5个数的和为(x+1)+(x-1)+(x+7)+(x-7)+x=5x.因此方框中5个数的和是方框正中心的数的5倍.【要点指导】整体思想是中学数学中的一种重要的思想方法.运 用整体方法解数学问题, 可以避开烦琐的计算, 使思路简捷明朗.特别是求式子的值时, 当式子中某未知字母的值不易求出时, 一般考虑将含未知字母的部分看成一个整体, 同时对所求多项式进行变形, 使它转化成含有被看成整体的部分, 再整体代入求值.素养提升专题一 整体思想例1 [泰州中考]若2a-b=5, 则多项式6a-3b的值是 . 15相关题1-1 [成都中考]已知当x=1时, 2ax2+bx的值为3, 则当x=2 时, ax2+bx的值为 . 6相关题1-2 [河北中考]若mn=m+3, 则 2mn+3m-5mn+10= .1专题二 探索规律【要点指导】常见的探索规律问题有两类:数式规律和图形规律. 探索数式的变化规律时, 把所给的式子做横向和纵向比较, 注意观察已知 的对应数值的变化, 从中发现数量关系, 即找出各部分所具有的特征, 从而探究出整个式子所具有的规律;探索图形的变化规律时, 一般需要抓住图形数量的增减变化特点, 进行分析、猜想、归纳、验证得出结果.例2 [遂宁中考] 为庆祝六一儿童节, 某幼儿园举行用火柴棒摆“金 鱼”比赛, 如图2-Z-4所示. 按照下面的规律, 摆第(n)个图需用火柴棒的根 数为 . (n是正整数)6n+2[n(n+1)+4]或(n2+n+4)相关题2-1 将一些半径相同的小圆按 图2-Z-5所示的规律摆放, 请仔细观察, 第 n (n是正整 数)个图形中有
个小 圆(用含n的
式子表示). 相关题2-2 下面是按一定规律排列的 一列数: 那么第n个数是 . (n 是正整数)中考链接母题1 (教材P60习题2.1第7题)
设n表示任意一个整数, 用含n的式子表示:
(1)任意一个偶数;(2)任意一个奇数. 考点:用字母表示数.
考情:用字母表示数是中考中常见的考点, 难度 不大.
策略:正确理解文字语言中的关键词, 找到其中 的数量关系.链接1 [安徽中考] 某企业今年3月份的产值 为a万元, 4月份比3月份减少了10%, 5月份比4月份 增加了15%, 则5月份的产值是( ).
A.(a-10%)(a+15%)万元 B.(1-10%)(1+15%)a万元
C.(a-10%+15%)万元 D.(1-10%+15%)a万元B分析 已知3月份的产值是a万元, 则4月份的 产值是(1-10%) a万元, 5月份的产值是(1-10%)(1+ 15%)a万元. 母题2 (教材P59习题2.1第3题)
填表: 考点:单项式的系数、次数及多项式的项、次数.
考情:单项式、多项式和整式的有关概念的考查 在中考中经常出现, 但分值不高.
策略:正确理解单项式的系数、次数及多项式 的项、次数的概念. D链接2 [铜仁中考] 单项式 的系数是( ). 二链接3 [湛江中考] 多项式2x2-3x+5是 次 项式.分析 多项式2x2-3x+5中含3个单项式, 最高 次项2x2的次数为2, 所以是二次三项式. 三母题3 (教材P69习题2.2第1题)
计算:(1)2x-10.3x; (2)3x-x-5x;
(3)-b+0.6b-2.6b; (4)m-n2+m-n2.考点:同类项、合并同类项.
考情:同类项的概念与合并同类项是中考的常见 考点.
策略:(1)应用同类项的概念求未知字母的值;
(2)根据合并同类项法则合并同类项. A链接4 [包头中考] 如果 是同类 项, 那么 的值是( ). C链接5 [淄博中考] 若单项式 的和仍是单项式, 则 的值是( ).
A.3 B.6 C.8 D.9 母题4 (教材P70习题2.2第4题)
先化简, 再求值:(-x2+5+4x)+(5x-4+2x2), 其中x=-2.考点:整式加减的运算, 化简求值.
考情:整式的加减是中考中重要的考点, 常常与整式的乘除结合起来考查.
策略:几个整式相加减, 通常用括号把每个整式括起来, 再用加减号连接, 然后去括号、合并同类项.链接6 [武汉中考] 先化简, 再求值:(3a2-2ab+b2)-(2a2+3ab-5b2), 其中a=-2, b=-1. 解 原式=3a2-2ab+b2-2a2-3ab+5b2
=a2-5ab+6b2.
当a=-2, b=-1时,
a2-5ab+6b2
=(-2) 2-5×(-2)×(-1)+6×(-1) 2
=4-10+6 =0.母题5 (教材P70习题2.2第8题)
某轮船顺水航行3 h, 逆水航行1.5 h, 已知轮船 在静水中的速度是a km/h, 水流速度是y km/h, 轮船 共航行多少千米?考点:列整式、整式的加减的实际应用.
考情:整式的加减在实际生活中的应用在中考中经常出现, 常见考题有销售问题、和差倍分问题、面积问题等.
策略:对待具体问题要注意:①运算顺序, 并要正确合理地使用括号;②特殊词语的含义, 如几倍、一半、大、小、多、少、增长、增长到等. B分析 设小长方形的长为y cm, 宽为x cm, 如图 2-Z-6, 则两块阴影部分的周长为2(n-x-x)+2y+ 2×2x+2(n-y)
=4n(cm). 链接7 [宁波中考] 把四 张形状、大小完全相同的小 长方形卡片(如图2-Z-6①)不重叠地放在一个底面为长方 形(长为m cm, 宽为n cm)的盒 子底部(如图2-Z-6②), 盒子底面未被卡片覆盖的 部分用阴影表示, 则图②中两块阴影部分的周长和是( ).
A.4m cm B.4n cm
C.2(m+n)cm D.4(m-n)cm母题6 (教材P70习题2.2第10题)
如图2-Z-7所示, 由一些点组成形如三角形的图形, 每条“边”(包括两个顶点)有n(n>1)个点, 每个图形总的点数S是多少?当n=5, 7, 11时, S是多少?考点:列式表示规律、整式的化简求值.
考情:动手操作型问题是中考的重要题型, 创新性强.
策略:根据图形的变化规律, 得出一般的结论. C链接8 [聊城中考] 如图2-Z-8, 用围棋子按 下面的规律摆图形, 则摆第n个图形需要围棋子的 枚数是( ).
A.5n B.5n-1 C.6n-1 D.2n2+1分析 本题可采用验证法, 第1个图形中有围 棋子5枚, 第2个图形中有围棋子11枚, 第3个图形 中有围棋子17枚, 符合这一规律的只有C选项. 也可以这样看, 第1个图形中有围棋子(1+4)枚, 第 2个图形中有围棋子(3+8)枚, 第3个图形中有围棋 子(5+12)枚……所以第n个图形中有围棋子(2n1)+4n=(6n-1)枚.
谢 谢 观 看!
A. 原价减去10元后再打 8折 B. 原价打8折后再减去 10元 C. 原价减去10元后再打 2折 D. 原价打2折后再减去 10元【要点指导】本专题主要是对“三式”和“四数”的考查.“三式” 即单项式、多项式和整式, “四数”是指单项式的系数与次数、多项式 的项数与次数. 解决这类问题的关键是熟记概念, 利用概念解题.专题二 整式的有关概念例2 下列各式中, 哪些是单项式?哪些是多项式?并指出单项式及 多项式的次数. 相关题2 (1)将
填入相应的括号中. 单项式:{ …}; 多项式:{ …}; 整式:{ …}. 相关题2 (2)填表3a,-1-x,5x2,7-2x2y,6xy4,-3.1253a5x26xy4一次二项式二次三项式五次三项式相关题2 (3)已知 的次数为 10, 则2m+2n-1的值为 . 17例3 已知多项式
(1)写出多项式各项的系数和次数;
(2)若多项式的次数为8, 求a的值. 分析 多项式每一项的系数包括它前面的符号, 不可以漏掉. π是常数不 是字母, 所以本题多项式中的第一项的系数与π有关, 而次数与π无关.相关题3 多项式 是六次三项式, 则m , n .≠-5=5【要点指导】同类项指所含字母相同, 并且相同字母的指数也相同的 项. 常常根据同类项中相同字母的指数相同建立等量关系列出方程.专题三 同类项与合并同类项 例4 若 是同类项, 则m+n的值为( ).
A.1 B.2 C.3 D.4 C分析 由题意, 得m=1, n=2, 所以m+n=1+2=3. 相关题4 若 的和是单 项式, 求2a+b的值.
解:因为-xa+1y4与4ybx2的和是单项式,
所以-xa+1y4与4ybx2是同类项,
所以a+1=2,b=4,
解得a=1,b=4,
所以2a+b=2×1+4=6.专题四 整式的加减【要点指导】整式加减的实质是去括号、合并同类项, 在去括号时注 意符号问题.例5 一名同学做一道题: “已知两个多项式A和B, 计算2A+B.”他误 将“2A+B”看成“A+2B” , 求得的结果为9x2-2x+7. 已知B=x2+3x-2, 请求 出2A+B的正确结果. 解 由题意, 得A=9x2-2x+7-2(x2+3x-2)=9x2-2x+7-2x2-6x+4=7x2-8x+11.
所以2A+B=2(7x2-8x+11)+(x2+3x-2)=14x2-16x+22+x2+3x-2=15x213x+20. 相关题5 有一道题目:“当x=100时, 求整式(8-7x-6x2+ x3 )+ (x3 +5x2+4x-1)-(-x2-3x+2x3 -3)的值.” 甲同学 做题时把x=100错抄成 x=10, 乙同学没抄错, 但他们得出来的结果却一样, 你能说明原因吗?解:因为(8-7x-6x2+x3)+(x3+5x2+4x-1)-(-x2-3x+2x3-3)=8-7x-6x2+x3+x3+5x2+4x-1+x2+3x-2x3+3=10,与字母x的取值无关,所以,当x=100和x=10时的计算结果是一样的.专题五 整式的化简求值【要点指导】整式的化简求值通常是先把整式化简, 然后再代入求值. 整式的化简求值有以下三类:一是化简后直接代入求值;二是化简 后整体代入求值;三是先通过隐含条件将字母的值求出, 再代入求值.分析 (1)先去括号、合并同类项, 再代入求值;(2)先将条件变形, 然 后代入求值;(3)利用非负性求出a,b的值.例6 (1)先化简, 再求值:
其中x=-3, y=1;
(2)已知x2+3x+5的值为7, 求式子3x2+9x-2的值;
(3)已知(a-2)2+|b+1|=0, 求3a2b-[2a2b-(2ab-a2b)-4a2]-ab的值. 解 (1)原式= x-2x+y- x+3y=-3x+4y.
当x=-3, y=1时, 原式=-3×(-3)+4×1=13.
(2)因为x2+3x+5的值为7, 所以x2+3x=2,
所以3x2+9x-2=3(x2+3x)-2=3×2-2=4.
(3)因为(a-2)2≥0, |b+1|≥0, 且(a-2)2+|b+1|=0,
所以a-2=0, b+1=0, 解得a=2, b=-1.
所以3a2b-[2a2b-(2ab-a2b)-4a2]-ab
=3a2b-(2a2b-2ab+a2b-4a2)-ab
=3a2b-2a2b+2ab-a2b+4a2-ab
=4a2+ab =4×22+2×(-1) =14. 相关题6 (1)先化简, 再求值:
其中x=-1, y=2;
已知2a-3b2=5, 求10-2a+3b2的值.专题六 整式加减在实际生活中的应用【要点指导】整式加减的实际应用, 主要是对生活中的实际问题列 式计算, 解决问题的关键是审清题意, 用式子正确表示实际问题中的数量关系.例7 小明乘公共汽车到城里的书店买书, 小明上车后, 发现车上共 有(3a-b+1)人, 车到中途站时, 下去(2a-3)人, 但又上来若干人, 这时公共 汽车上共有(8a-5b)人, 则中途上车多少人?当a=5, b=6时, 中途上车多 少人? 分析 中途上车的乘客数=现有乘客数-原有乘客数+中途下车的乘 客数. 解:中途上车人数为(8a-5b) -(3a-b+1) +(2a-3)=8a-5b-3a+b1+2a-3=7a-4b-4. 当a=5, b=6时, 中途上车7a-4b-4=7×5-4×6-4=7(人). 相关题7 汛期来临前, 滨海区决定 实施“海堤加固”工程, 某 工程队承包了该项目, 计 划每天加固60米.在施工 前, 得到气象部门的预报,近期有台风袭击滨海区, 于 是工程队改变计划, 每天加 固的海堤长度是原计划的 1.5倍, 这样赶在台风来临 前完成加固任务.设滨海区 要加固的海堤长为a米, 则 完成整个任务的实际时间 比原计划少用了 天 (用含a的式子表示). 专题七 程序运算问题【要点指导】若是单一程序, 则可列出程序式求解;若程序有多 种模式, 则要根据输入的数据选择恰当的程序式求解;若程序中含有 “是”“否”, 则可逐步计算求解. 另外, 若已知输出结果求输入的数值, 应逆向思考, 但要注意, 程序中的每一步运算都要变为相应的逆运算.6例8 如图2-Z-1所示的运算程序中, 若开始输入的x值为48, 我们发 现第1次输出的结果为24, 第2次输出的结果为12……则第2019次输出的结 果为 .从表中可看出, 第3次输出的结果为6, 第4次输出的结果为3, 第5次输 出的结果为6, 第6次输出的结果为3, 第7次输出的结果为6, 第8次输出的结 果为3, 第9次输出的结果为6, 第10次输出的结果为3……即从第3次开始, 第奇数次输出的结果为偶数6, 第偶数次输出的结果为奇数3, 所以第2019 次输出的结果为6.相关题8 如图2-Z-2所示的运算程 序中, 若开始输入x=-1,则 最后输出的结果是 .-9专题八 月历中的学问【要点指导】月历中, 每行的数都是从小到大排列的, 后一个数比前 一个大1;每列中下一个数总比上一个大7;从右上方往左下方, 左下方 的数都比右上方的数大6;从左上方往右下方, 右下方的数都比左上方的 数大8.例9 假如老师在假期外出旅行一周, 这一周在同一个月, 你能帮老 师算一算, 这七天的日期之和与外出第四天的日期有什么关系吗?分析 设外出第四天的日期为x, 则其他各天的日期分别为x-1, x+1, x-2, x+2, x-3, x+3.解:这七天的日期之和为(x+1)+(x-1)+(x+2)+(x-2)+(x+3)+(x3)+x=7x, 所以可以发现这七天的日期之和是第四天的日期的7倍.相关题9 如图2-Z-3是某月的月历.
(1)带阴影的方框中的5个 数的和与方框正中心的数 有什么关系?
(2)如果将带阴影的方框移 动到其他位置, 还能得到上 述结论吗?用你所学的知 识说明理由.解: (1)2+9+16+8+10=45.方框中5个数的和是方框正中心的数的5倍.
(2)还能得到上面的结论.理由如下:
设正中间方框中的数为x,则其他的4个数分别为x+1,x-1,x+7,x-7.所以这5个数的和为(x+1)+(x-1)+(x+7)+(x-7)+x=5x.因此方框中5个数的和是方框正中心的数的5倍.【要点指导】整体思想是中学数学中的一种重要的思想方法.运 用整体方法解数学问题, 可以避开烦琐的计算, 使思路简捷明朗.特别是求式子的值时, 当式子中某未知字母的值不易求出时, 一般考虑将含未知字母的部分看成一个整体, 同时对所求多项式进行变形, 使它转化成含有被看成整体的部分, 再整体代入求值.素养提升专题一 整体思想例1 [泰州中考]若2a-b=5, 则多项式6a-3b的值是 . 15相关题1-1 [成都中考]已知当x=1时, 2ax2+bx的值为3, 则当x=2 时, ax2+bx的值为 . 6相关题1-2 [河北中考]若mn=m+3, 则 2mn+3m-5mn+10= .1专题二 探索规律【要点指导】常见的探索规律问题有两类:数式规律和图形规律. 探索数式的变化规律时, 把所给的式子做横向和纵向比较, 注意观察已知 的对应数值的变化, 从中发现数量关系, 即找出各部分所具有的特征, 从而探究出整个式子所具有的规律;探索图形的变化规律时, 一般需要抓住图形数量的增减变化特点, 进行分析、猜想、归纳、验证得出结果.例2 [遂宁中考] 为庆祝六一儿童节, 某幼儿园举行用火柴棒摆“金 鱼”比赛, 如图2-Z-4所示. 按照下面的规律, 摆第(n)个图需用火柴棒的根 数为 . (n是正整数)6n+2[n(n+1)+4]或(n2+n+4)相关题2-1 将一些半径相同的小圆按 图2-Z-5所示的规律摆放, 请仔细观察, 第 n (n是正整 数)个图形中有
个小 圆(用含n的
式子表示). 相关题2-2 下面是按一定规律排列的 一列数: 那么第n个数是 . (n 是正整数)中考链接母题1 (教材P60习题2.1第7题)
设n表示任意一个整数, 用含n的式子表示:
(1)任意一个偶数;(2)任意一个奇数. 考点:用字母表示数.
考情:用字母表示数是中考中常见的考点, 难度 不大.
策略:正确理解文字语言中的关键词, 找到其中 的数量关系.链接1 [安徽中考] 某企业今年3月份的产值 为a万元, 4月份比3月份减少了10%, 5月份比4月份 增加了15%, 则5月份的产值是( ).
A.(a-10%)(a+15%)万元 B.(1-10%)(1+15%)a万元
C.(a-10%+15%)万元 D.(1-10%+15%)a万元B分析 已知3月份的产值是a万元, 则4月份的 产值是(1-10%) a万元, 5月份的产值是(1-10%)(1+ 15%)a万元. 母题2 (教材P59习题2.1第3题)
填表: 考点:单项式的系数、次数及多项式的项、次数.
考情:单项式、多项式和整式的有关概念的考查 在中考中经常出现, 但分值不高.
策略:正确理解单项式的系数、次数及多项式 的项、次数的概念. D链接2 [铜仁中考] 单项式 的系数是( ). 二链接3 [湛江中考] 多项式2x2-3x+5是 次 项式.分析 多项式2x2-3x+5中含3个单项式, 最高 次项2x2的次数为2, 所以是二次三项式. 三母题3 (教材P69习题2.2第1题)
计算:(1)2x-10.3x; (2)3x-x-5x;
(3)-b+0.6b-2.6b; (4)m-n2+m-n2.考点:同类项、合并同类项.
考情:同类项的概念与合并同类项是中考的常见 考点.
策略:(1)应用同类项的概念求未知字母的值;
(2)根据合并同类项法则合并同类项. A链接4 [包头中考] 如果 是同类 项, 那么 的值是( ). C链接5 [淄博中考] 若单项式 的和仍是单项式, 则 的值是( ).
A.3 B.6 C.8 D.9 母题4 (教材P70习题2.2第4题)
先化简, 再求值:(-x2+5+4x)+(5x-4+2x2), 其中x=-2.考点:整式加减的运算, 化简求值.
考情:整式的加减是中考中重要的考点, 常常与整式的乘除结合起来考查.
策略:几个整式相加减, 通常用括号把每个整式括起来, 再用加减号连接, 然后去括号、合并同类项.链接6 [武汉中考] 先化简, 再求值:(3a2-2ab+b2)-(2a2+3ab-5b2), 其中a=-2, b=-1. 解 原式=3a2-2ab+b2-2a2-3ab+5b2
=a2-5ab+6b2.
当a=-2, b=-1时,
a2-5ab+6b2
=(-2) 2-5×(-2)×(-1)+6×(-1) 2
=4-10+6 =0.母题5 (教材P70习题2.2第8题)
某轮船顺水航行3 h, 逆水航行1.5 h, 已知轮船 在静水中的速度是a km/h, 水流速度是y km/h, 轮船 共航行多少千米?考点:列整式、整式的加减的实际应用.
考情:整式的加减在实际生活中的应用在中考中经常出现, 常见考题有销售问题、和差倍分问题、面积问题等.
策略:对待具体问题要注意:①运算顺序, 并要正确合理地使用括号;②特殊词语的含义, 如几倍、一半、大、小、多、少、增长、增长到等. B分析 设小长方形的长为y cm, 宽为x cm, 如图 2-Z-6, 则两块阴影部分的周长为2(n-x-x)+2y+ 2×2x+2(n-y)
=4n(cm). 链接7 [宁波中考] 把四 张形状、大小完全相同的小 长方形卡片(如图2-Z-6①)不重叠地放在一个底面为长方 形(长为m cm, 宽为n cm)的盒 子底部(如图2-Z-6②), 盒子底面未被卡片覆盖的 部分用阴影表示, 则图②中两块阴影部分的周长和是( ).
A.4m cm B.4n cm
C.2(m+n)cm D.4(m-n)cm母题6 (教材P70习题2.2第10题)
如图2-Z-7所示, 由一些点组成形如三角形的图形, 每条“边”(包括两个顶点)有n(n>1)个点, 每个图形总的点数S是多少?当n=5, 7, 11时, S是多少?考点:列式表示规律、整式的化简求值.
考情:动手操作型问题是中考的重要题型, 创新性强.
策略:根据图形的变化规律, 得出一般的结论. C链接8 [聊城中考] 如图2-Z-8, 用围棋子按 下面的规律摆图形, 则摆第n个图形需要围棋子的 枚数是( ).
A.5n B.5n-1 C.6n-1 D.2n2+1分析 本题可采用验证法, 第1个图形中有围 棋子5枚, 第2个图形中有围棋子11枚, 第3个图形 中有围棋子17枚, 符合这一规律的只有C选项. 也可以这样看, 第1个图形中有围棋子(1+4)枚, 第 2个图形中有围棋子(3+8)枚, 第3个图形中有围棋 子(5+12)枚……所以第n个图形中有围棋子(2n1)+4n=(6n-1)枚.
谢 谢 观 看!
