人教版数学九年级上册第25章:概率初步复习课件(71张PPT)
文档属性
| 名称 | 人教版数学九年级上册第25章:概率初步复习课件(71张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-21 11:28:12 | ||
图片预览







文档简介
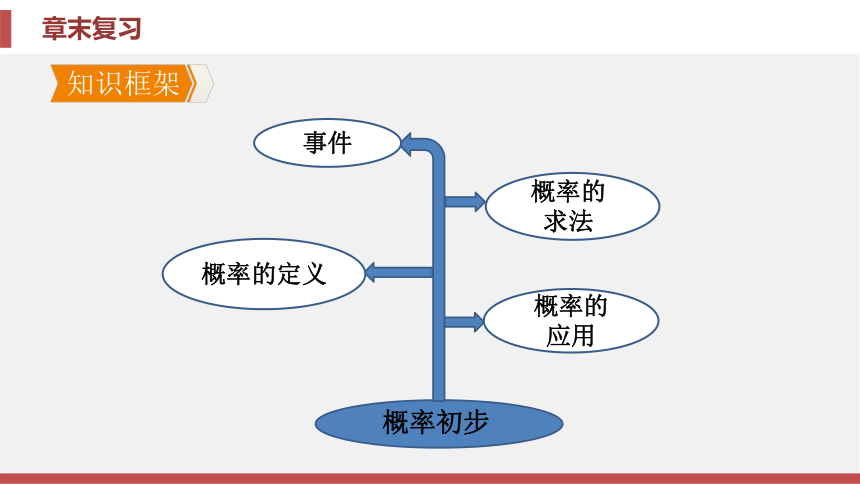
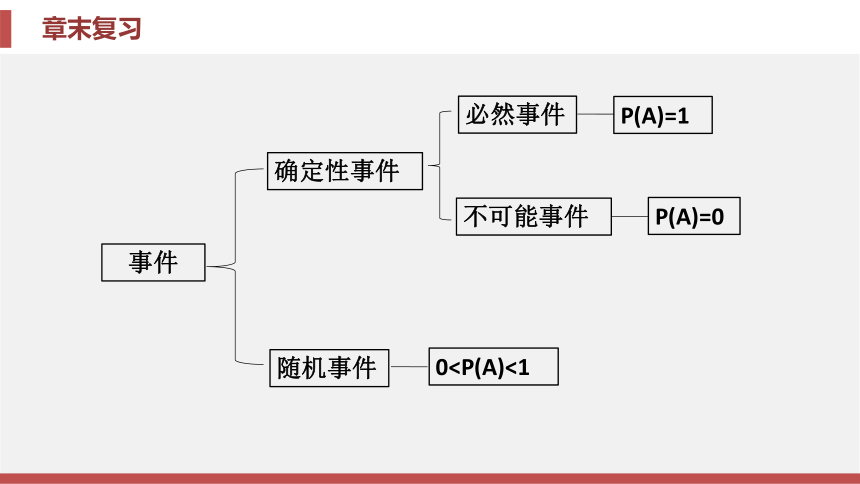
课件71张PPT。第二十五章 概率初步章末复习第二十五章 概率初步章末复习知识框架归纳整合素养提升中考链接知识框架确定性事件不可能事件必然事件随机事件P(A)=0P(A)=10A.对顶角相等 B.内错角相等
C.三角形的内角和等于180° D.2020年1月有31天B 相关题1 下列事件是随机事件的是 ( ).
A. 在标准大气压下, 水加 热到100 ℃时沸腾
B. 购买一张福利彩票, 中 奖3000万
C. 有一名运动员奔跑的 速度是30米/秒
D. 从一个仅装着红球的 袋中摸球, 摸出红球 B【要点指导】概率是反映事件发生的可能性大小的量, 必然事件发生 的概率为1, 不可能事件发生的概率为0, 随机事件发生的概率在0与1之间.专题二 概率的意义 A例2 下列说法中, 正确的是( ).
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次, 正面朝上的次数一定为50次相关题2 明天的降水概率为80%的 含义有以下三种不同的解 释:①明天80%的地区会 下雨; ②80%的人认为明 天会下雨;③明天下雨的 可能性比较大. 你认为其 中合理的解释是_______(写出序号即可).
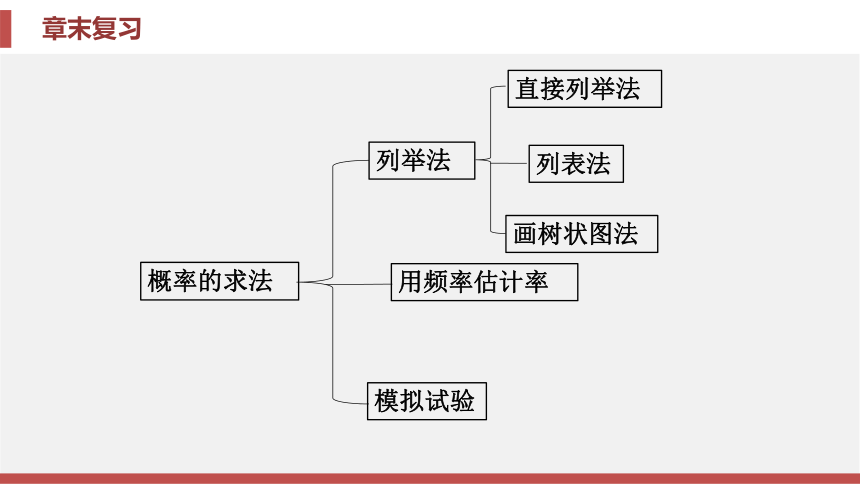
③专题三 用列举法求简单事件的概率【要点指导】求等可能事件的概率时, 可先求出试验发生的总结果 数n和事件A发生的结果数m, 然后利用公式P(A)= 计算出事件A发生的概 率.当一次试验涉及两个因素时, 可采用列表法或画树状图的方法列举所 有等可能的结果;当一次试验涉及三个或三个以上的因素时, 应采用画树 状图的方法列举所有等可能的结果.例3 一个不透明的袋子中装有4个黑球, 2个白球, 这些球除颜色不同 外其他都相同, 从袋子中随机摸出1个球, 摸到黑球的概率是( ). D相关题3 如果从包括小军在内的 10名大学生中任选1名作 为“保护母亲河”的志愿 者, 那么小军被选中的概 率是( ).
C例4 在校园文化艺术节中, 九年级一班有1名男生和2名女生获得美 术奖, 另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会, 求刚好 是男生的概率;
(2)从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 用列表 或画树状图的方法求刚好是1名男生、1名女生的概率. 解 (1)获奖的学生中男生3名, 女生4名, 男生、女生共7名, 故参加颁奖大会的学生是男生的概率为 .
(2)从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 用列表法列出所有可能的结果如下: ∵共有12种等可能的结果, 其中是1名男生、1名女生的结果有6种,
∴从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 刚好是
1名男生、1名女生的概率为相关题4 用图25-Z-1中两个可自 由转动的转盘做“配紫 色”游戏, 分别转动两个 转盘, 若其中一个转出红 色, 另一个转出蓝色即可 配成紫色(指针指向分界 线时重转), 那么可配成紫 色的概率是( ).B【要点指导】试验中, 某事件发生的次数与总次数的比值叫作频率. 对于一般的随机事件, 在大量重复试验中, 随着试验次数的增加, 事件发 生的频率会稳定在一个数值附近, 所以可以通过大量的重复试验, 用一 个随机事件发生的频率去估计它的概率.专题四 用频率估计概率例5 色盲是伴X染色体隐性先天遗传病, 患者中男性远多于女生, 从 男性体检信息库中随机抽取体检表, 统计结果如下表:
根据表中数据, 估计在男性中, 男性患色盲的概率为_______ (结果保留小数点后两位). 0.07分析 观察表格发现, 随着抽取的体检表的增多, 在男性中, 男性患色 盲的频率逐渐稳定在0.07附近, 所以估计在男性中, 男生患色盲的概率为 0.07. 相关题5 在一个不透明的布袋中, 有黄色、白色的玻璃球共 10个, 它们除颜色不同外, 形状、大小、质地等完全 相同.小刚通过多次摸球 试验后发现, 摸到黄色球 的频率稳定在40%, 则布 袋中白色球的个数很可能 是( )
A.4 B.5 C.6 D.7C解析 根据题意,估计摸到黄色球的概率为40%,则摸到白色球的概率=1-40%=60%,所以口袋中白色球的个数=10×60%=6,即布袋中白色球的个数很可能是6.故选C.【要点指导】通过计算概率判断游戏是否公平是概率知识的一个 重要应用, 解决游戏是否公平的问题, 应先计算游戏参与者获胜的概率, 若概率相等, 则游戏公平;若概率不相等, 则游戏不公平.专题五 利用概率判断游戏的公平性例6 小莉的爸爸买了一张动物园的门票, 她和哥哥都很想去, 可门票 只有一张, 于是哥哥想了一个办法, 他拿出八张扑克牌, 将数字为1, 2, 3, 5的 四张牌给了小莉, 将数字为4, 6, 7, 8的四张牌留给自己, 并按如下规则进行: 小莉和哥哥分别从各自的四张牌中随机抽出一张, 然后将抽出的两张扑克牌 上的数字相加, 若和为偶数, 则小莉去;若和为奇数, 则哥哥去.
(1)求小莉去动物园的概率.
(2)哥哥设计的规则公平吗?若公平, 请说明理由;若不公平, 请你设 计一种公平的规则. 解 (1)列表如下:
或画树状图如图25-Z-2:由上表(或树状图)可以看出一共有16种等可能的结果, 其中和为偶数 的结果有6种, 所以P(和为偶数)= , 即小莉去动物园的概率为 . (2)由(1)中的表格(或树状图)可以看出和为奇数的结果有10种, 所以
P(和为奇数)= , 则哥哥去动物园的概率为 . 由(1)知小莉去动
物园的概率为 , 所以哥哥设计的规则不公平.
规则改为:若和为偶数, 则小莉得5分;若和为奇数, 则哥哥得3分,
得分多者去(答案不唯一).相关题6 有四张正面写有数字的卡 片, 如图25-Z-3所示, 这 些卡片除数字不同外其余 完全相同, 将它们洗匀后, 背面朝上放置在桌面上.
(1)从中随机抽取一张卡 片, 求恰好抽到数字2的 概率;
(2)小贝和小晶想用以上 四张卡片做游戏, 游戏规 则如图25-Z-4.你认为这 个游戏公平吗?请说明理 由. 若不公平,
请你修改规 则, 使游戏变得公平.【要点指导】若事件的概率与图形的面积有关, 则事件发生的概率 等于该事件发生的可能结果组成的图形的面积除以所有可能结果组成 的图形的面积.专题六 求与图形面积有关的概率例7 “赵爽弦图”是由四个全等的直角三角形与中间 一个小正方形拼成的大正方形. 图25-Z-5是一个“赵爽弦 图”飞镖板, 其中直角三角形的两条直角边的长分别是2和4. 小明同学在距飞镖板一定距离处向飞镖板投掷飞镖(假设投 掷的飞镖均扎在飞
镖板上), 则投掷一次飞镖恰好扎在中间小正方形区域
的 概率是( ). C分析 根据题意, 得整个图形是正方形, 面积为22+42=20. 中间小正方形 的边长为4-2=2, 所以中间小正方形的面积为4, 所以P(飞镖扎在中间小正方 形区域)=相关题7 如图25-Z-6, 正方形 ABCD内接于⊙O,⊙O的直 径为 分米, 若在这个圆 面上随意抛一粒豆子, 则 豆子落在正方形ABCD区 域内的概率是( ).A【要点指导】概率与统计和人们的生活密切相关, 在生产、生活和 科研等各个方面都有广泛的应用. 解决此类问题, 要善于从统计图表中 获取有用的信息, 分析研究后才能做出正确的判断, 进而解决问题. 专题七 概率与统计的综合应用例8 [天水中考] 八年级(一)班开展了“读一本好书”的活动, 班 委会对学生阅读书籍的情况进行了问卷调查, 问卷设置了“小说”
“戏 剧”“散文”“其他”四个类别, 每位同学仅选一项, 根据调查结果绘制了 如下不完整的频数分布表和扇形统计图. 根据图表提供的信息, 解答下列问题:
(1)八年级(一)班共有多少位学生?
(2)请补全频数分布表, 并求出扇形统计图中“其他”类所占的百 分比;
(3)在问卷调查中, 甲、乙、丙、丁4位同学选择了“戏剧”类, 现从以 上4位同学中任意选出2位同学参加学校的戏剧兴趣小组, 请用画树状图或 列表的方法, 求选取的2人恰好是乙和丙的概率. 解 (1)∵喜欢散文的学生共有10人, 频率为0.25, ∴学生总人数=10÷0.25=40. 答:八年级(一)班共有40位学生.
(2)频数分布表从左到右、从上到下依次填:20, 0.1, 0.15, 40. 在扇形统计图中, “其他”类所占的百分比为 ×100%=15%.
(3)画树状图, 如图25-Z-8所示:
所有等可能的情况有12种, 其中选取的2人恰好是乙与丙的情况有2种,
∴P(选取的2人恰好是乙和丙)=素养提升【要点指导】当已知某个事件发生的概率, 求事件发生的可能情况 时, 可以借助方程思想, 以概率公式为等量关系式, 列方程求解.专题 方程思想在概率中的应用例 在一个不透明的布袋中, 装有红、黑、白三种只有颜色不同的小 球, 其中红色小球有4个, 黑、白两种颜色的小球的数目相同. 小明从布袋中 随机摸出1个球, 记下颜色后放回布袋中, 摇匀后再随机摸出1个球, 记下颜 色后放回布袋中……如此进行大量重复摸球试验后, 小明发现摸出红色小 球的频率稳定于20%, 由此可以估计布袋中的黑色小球有________个. 8分析 设黑色小球有x个, 则黑、白两种颜色的小球一共有2x个. ∵经过多次试验后发现摸到红色小球的频率稳定于20%, ∴可估计摸到 红色小球的概率为20%, ∴4=20%(4+2x), 解得x=8, ∴黑色小球有8个.相关题 在一个不透明的布袋中装 有若干个只有颜色不同的 小球, 如果袋中有红球5个, 黄球4个, 其余为白球, 从袋 子中随机摸出1个球, “摸出黄球”的概率为 , 那么袋中白球的个数为( ).
A.2 B.3
C.4 D.12B中考链接母题1 事件类型的判别(教材P134习题25.1第 1题)
请指出在下列事件中, 哪些是随机事件, 哪些 是必然事件, 哪些是不可能事件. (1)通常温度降到0 ℃以下, 纯净的水结冰; (2)随意翻到一本书的某页, 这页的页码是奇数; (3)从地面发射1枚导弹, 未击中空中目标;(4)明天 太阳从东方升起;(5)汽车累积行驶10 000 km, 从 未出现故障;(6)购买1张彩票, 中奖. 考点:随机事件、必然事件、不可能事件的 概念.
考情:随机事件、必然事件、不可能事件的判 别是常考知识点.
策略:根据三种事件的概念解题, 在一定条件下, 判断哪些事件必然会发生, 哪些事件必然不会发 生, 哪些事件可能发生也可能不发生. 链接1 [漳州中考]下列事件中, 属于必然事件 的是( ).
A.打开电视机, 正在播广告
B.打开数学书, 恰好翻到第50页
C.抛掷一枚质地均匀的硬币, 恰好正面朝上
D.一天有24小时 D母题2 概率计算公式(教材P134习题25.1第4题) 一个质地均匀的小正方体, 六个面分别标有数 字“1”“1”“2”“4”“5”“5”. 掷小正方体后, 观 察朝上一面的数字.
(1)出现“5”的概率是多少?
(2)出现“6”的概率是多少?
(3)出现奇数的概率是多少?考点:概率的计算公式P(A)= .
考情:概率的计算是中考的热点, 近年来还出 现了概率与几何图形、函数、统计等相结合的 试题.
策略:根据所给的条件, 列举所有可能的结果和 事件A包含的可能的结果, 进而利用概率的计算 公式进行计算. 链接2 [攀枝花中考]布袋中装有除颜色外没 有其他区别的1个红球和2个白球, 搅匀后从中摸出 1个球, 放回搅匀, 再摸出1个球, 两次都摸出白球的 概率是( ).
A母题3 与几何有关的概率(教材P134习题25.1第 5题) 如图25-Z-10是一个可以自由转 动的质地均匀的转盘, 被分成12个相 同的扇形. 请你在转盘的适当地方涂 上红、蓝两种颜色, 使得转动的转盘 停止时, 指针指向红、蓝两色的概
率分别为考点:概率的计算公式P= , 几何图形的面积公 式与几何图形的有关性质.
考情:概率与几何的结合是中考的常考考点, 题 型以填空题、选择题为主.
策略:把求概率问题转化为求几何图形的面积 比或者几何图形性质的分类讨论问题或几何计 数问题. 链接3 [山西中考]小江 玩投掷飞镖的游戏, 他设计 了一个如图25-Z-11所示的 靶子, E, F分别是矩形ABCD 的边AD, BC上的点, 且EF∥AB, M, N是EF上的任 意两点, 则投掷一次, 飞镖落在阴影部分的概率是 ( ). C分析 ∵矩形ABFE内阴影部分的面积= × 矩形ABFE的面积, 矩形DCFE内阴影部分的面积= ×矩形DCFE的面积,
∴阴影部分的面积= ×矩形ABCD的面积,
∴飞镖落在阴影部分的概率是 . 故选C. 母题4 用列表法或画树状图法求概率(教材P138练 习第2题) 有6张看上去无差别的卡片, 上面分别写着1, 2, 3, 4, 5, 6. 随机抽取1张后, 放回并混在一起, 再随 机抽取1张, 那么第二次取出的数字能够整除第一 次取出的数字的概率是多少?考点:概率的计算公式P= .
考情:利用列表法或画树状图法求概率是中考 的热点, 常见的考查方式是求某一事件的概率.
策略:利用列表法或画树状图法求概率. 链接4 [无锡中考](1)甲、乙、丙、丁四人做 传球游戏:第一次由甲将球随机传给乙、丙、丁 中的某一人, 从第二次起, 每一次都由持球者将球 再随机传给其他三人中的某一人. 求第二次传球后 球回到甲手里的概率(请用画树状图或列表的方法 给出分析过程).
(2)如果甲和另外n(n≥2)个人做(1)中同样的 游戏, 那么第三次传球后球回到甲手里的概率是______(请直接写结果). 解 (1)画树状图如图25-Z-12. ∵共有9种等可能的结果, 其 中符合要求的结果有3种, ∴P(第二次传球后球回到甲 手里)=
(2)∵第三次传球的结果 总数是n3, 传给甲的结果数是 n(n-1),
∴第三次传球后球回到甲手里的概率是
故答案为
母题5 判断游戏的公平性(教材P153复习题25第 8题)
同学们, 你们都知道“石头、剪子、布”的游 戏吧!如果两个人做这种游戏, 随机出手一次, 两 个人获胜的概率各是多少?考点:概率的计算, 用列表法或画树状图法求事 件的概率.
考情:利用概率判断游戏的公平性是中考的热点.
策略:看一个游戏是否公平, 只要看游戏双方赢 的机会是否相同, 如果相同, 那么游戏公平;如 果不相同, 那么游戏不公平, 要使游戏变得公平, 就要修改它的规则. 链接5 [广州中考]在一个不透明的口袋里装 有分别标有数字2, 4, 6的3个小球(小球除数字不同 外其余都相同), 另有3张背面完全一样、正面分别 写有数字6, 7, 8的卡片. 现从口袋中任意摸出1个 小球, 再从这3张背面朝上的卡片中任意摸出1张 卡片. (1)请你用列表或画树状图的方法, 表示出所 有可能出现的结果; (2)小红和小莉做游戏, 制定了两个游戏 规则: 规则1:若两次摸出的数字至少有一次是 “6”, 则小红赢;否则小莉赢. 规则2:若摸出的卡片上的数字是球上数字的 整数倍, 则小红赢;否则小莉赢. 小红要想在游戏中获胜, 她应选择哪一种规 则?并说明理由. 解 (1)列表如下:
(2)小红应选择规则1. 理由: 规则1:P(小红赢)= ;规则2:P(小红 赢)= . ∵ , ∴小红应选择规则1.
谢 谢 观 看!
C.三角形的内角和等于180° D.2020年1月有31天B 相关题1 下列事件是随机事件的是 ( ).
A. 在标准大气压下, 水加 热到100 ℃时沸腾
B. 购买一张福利彩票, 中 奖3000万
C. 有一名运动员奔跑的 速度是30米/秒
D. 从一个仅装着红球的 袋中摸球, 摸出红球 B【要点指导】概率是反映事件发生的可能性大小的量, 必然事件发生 的概率为1, 不可能事件发生的概率为0, 随机事件发生的概率在0与1之间.专题二 概率的意义 A例2 下列说法中, 正确的是( ).
A.不可能事件发生的概率为0
B.随机事件发生的概率为
C.概率很小的事件不可能发生
D.投掷一枚质地均匀的硬币100次, 正面朝上的次数一定为50次相关题2 明天的降水概率为80%的 含义有以下三种不同的解 释:①明天80%的地区会 下雨; ②80%的人认为明 天会下雨;③明天下雨的 可能性比较大. 你认为其 中合理的解释是_______(写出序号即可).
③专题三 用列举法求简单事件的概率【要点指导】求等可能事件的概率时, 可先求出试验发生的总结果 数n和事件A发生的结果数m, 然后利用公式P(A)= 计算出事件A发生的概 率.当一次试验涉及两个因素时, 可采用列表法或画树状图的方法列举所 有等可能的结果;当一次试验涉及三个或三个以上的因素时, 应采用画树 状图的方法列举所有等可能的结果.例3 一个不透明的袋子中装有4个黑球, 2个白球, 这些球除颜色不同 外其他都相同, 从袋子中随机摸出1个球, 摸到黑球的概率是( ). D相关题3 如果从包括小军在内的 10名大学生中任选1名作 为“保护母亲河”的志愿 者, 那么小军被选中的概 率是( ).
C例4 在校园文化艺术节中, 九年级一班有1名男生和2名女生获得美 术奖, 另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会, 求刚好 是男生的概率;
(2)从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 用列表 或画树状图的方法求刚好是1名男生、1名女生的概率. 解 (1)获奖的学生中男生3名, 女生4名, 男生、女生共7名, 故参加颁奖大会的学生是男生的概率为 .
(2)从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 用列表法列出所有可能的结果如下: ∵共有12种等可能的结果, 其中是1名男生、1名女生的结果有6种,
∴从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会, 刚好是
1名男生、1名女生的概率为相关题4 用图25-Z-1中两个可自 由转动的转盘做“配紫 色”游戏, 分别转动两个 转盘, 若其中一个转出红 色, 另一个转出蓝色即可 配成紫色(指针指向分界 线时重转), 那么可配成紫 色的概率是( ).B【要点指导】试验中, 某事件发生的次数与总次数的比值叫作频率. 对于一般的随机事件, 在大量重复试验中, 随着试验次数的增加, 事件发 生的频率会稳定在一个数值附近, 所以可以通过大量的重复试验, 用一 个随机事件发生的频率去估计它的概率.专题四 用频率估计概率例5 色盲是伴X染色体隐性先天遗传病, 患者中男性远多于女生, 从 男性体检信息库中随机抽取体检表, 统计结果如下表:
根据表中数据, 估计在男性中, 男性患色盲的概率为_______ (结果保留小数点后两位). 0.07分析 观察表格发现, 随着抽取的体检表的增多, 在男性中, 男性患色 盲的频率逐渐稳定在0.07附近, 所以估计在男性中, 男生患色盲的概率为 0.07. 相关题5 在一个不透明的布袋中, 有黄色、白色的玻璃球共 10个, 它们除颜色不同外, 形状、大小、质地等完全 相同.小刚通过多次摸球 试验后发现, 摸到黄色球 的频率稳定在40%, 则布 袋中白色球的个数很可能 是( )
A.4 B.5 C.6 D.7C解析 根据题意,估计摸到黄色球的概率为40%,则摸到白色球的概率=1-40%=60%,所以口袋中白色球的个数=10×60%=6,即布袋中白色球的个数很可能是6.故选C.【要点指导】通过计算概率判断游戏是否公平是概率知识的一个 重要应用, 解决游戏是否公平的问题, 应先计算游戏参与者获胜的概率, 若概率相等, 则游戏公平;若概率不相等, 则游戏不公平.专题五 利用概率判断游戏的公平性例6 小莉的爸爸买了一张动物园的门票, 她和哥哥都很想去, 可门票 只有一张, 于是哥哥想了一个办法, 他拿出八张扑克牌, 将数字为1, 2, 3, 5的 四张牌给了小莉, 将数字为4, 6, 7, 8的四张牌留给自己, 并按如下规则进行: 小莉和哥哥分别从各自的四张牌中随机抽出一张, 然后将抽出的两张扑克牌 上的数字相加, 若和为偶数, 则小莉去;若和为奇数, 则哥哥去.
(1)求小莉去动物园的概率.
(2)哥哥设计的规则公平吗?若公平, 请说明理由;若不公平, 请你设 计一种公平的规则. 解 (1)列表如下:
或画树状图如图25-Z-2:由上表(或树状图)可以看出一共有16种等可能的结果, 其中和为偶数 的结果有6种, 所以P(和为偶数)= , 即小莉去动物园的概率为 . (2)由(1)中的表格(或树状图)可以看出和为奇数的结果有10种, 所以
P(和为奇数)= , 则哥哥去动物园的概率为 . 由(1)知小莉去动
物园的概率为 , 所以哥哥设计的规则不公平.
规则改为:若和为偶数, 则小莉得5分;若和为奇数, 则哥哥得3分,
得分多者去(答案不唯一).相关题6 有四张正面写有数字的卡 片, 如图25-Z-3所示, 这 些卡片除数字不同外其余 完全相同, 将它们洗匀后, 背面朝上放置在桌面上.
(1)从中随机抽取一张卡 片, 求恰好抽到数字2的 概率;
(2)小贝和小晶想用以上 四张卡片做游戏, 游戏规 则如图25-Z-4.你认为这 个游戏公平吗?请说明理 由. 若不公平,
请你修改规 则, 使游戏变得公平.【要点指导】若事件的概率与图形的面积有关, 则事件发生的概率 等于该事件发生的可能结果组成的图形的面积除以所有可能结果组成 的图形的面积.专题六 求与图形面积有关的概率例7 “赵爽弦图”是由四个全等的直角三角形与中间 一个小正方形拼成的大正方形. 图25-Z-5是一个“赵爽弦 图”飞镖板, 其中直角三角形的两条直角边的长分别是2和4. 小明同学在距飞镖板一定距离处向飞镖板投掷飞镖(假设投 掷的飞镖均扎在飞
镖板上), 则投掷一次飞镖恰好扎在中间小正方形区域
的 概率是( ). C分析 根据题意, 得整个图形是正方形, 面积为22+42=20. 中间小正方形 的边长为4-2=2, 所以中间小正方形的面积为4, 所以P(飞镖扎在中间小正方 形区域)=相关题7 如图25-Z-6, 正方形 ABCD内接于⊙O,⊙O的直 径为 分米, 若在这个圆 面上随意抛一粒豆子, 则 豆子落在正方形ABCD区 域内的概率是( ).A【要点指导】概率与统计和人们的生活密切相关, 在生产、生活和 科研等各个方面都有广泛的应用. 解决此类问题, 要善于从统计图表中 获取有用的信息, 分析研究后才能做出正确的判断, 进而解决问题. 专题七 概率与统计的综合应用例8 [天水中考] 八年级(一)班开展了“读一本好书”的活动, 班 委会对学生阅读书籍的情况进行了问卷调查, 问卷设置了“小说”
“戏 剧”“散文”“其他”四个类别, 每位同学仅选一项, 根据调查结果绘制了 如下不完整的频数分布表和扇形统计图. 根据图表提供的信息, 解答下列问题:
(1)八年级(一)班共有多少位学生?
(2)请补全频数分布表, 并求出扇形统计图中“其他”类所占的百 分比;
(3)在问卷调查中, 甲、乙、丙、丁4位同学选择了“戏剧”类, 现从以 上4位同学中任意选出2位同学参加学校的戏剧兴趣小组, 请用画树状图或 列表的方法, 求选取的2人恰好是乙和丙的概率. 解 (1)∵喜欢散文的学生共有10人, 频率为0.25, ∴学生总人数=10÷0.25=40. 答:八年级(一)班共有40位学生.
(2)频数分布表从左到右、从上到下依次填:20, 0.1, 0.15, 40. 在扇形统计图中, “其他”类所占的百分比为 ×100%=15%.
(3)画树状图, 如图25-Z-8所示:
所有等可能的情况有12种, 其中选取的2人恰好是乙与丙的情况有2种,
∴P(选取的2人恰好是乙和丙)=素养提升【要点指导】当已知某个事件发生的概率, 求事件发生的可能情况 时, 可以借助方程思想, 以概率公式为等量关系式, 列方程求解.专题 方程思想在概率中的应用例 在一个不透明的布袋中, 装有红、黑、白三种只有颜色不同的小 球, 其中红色小球有4个, 黑、白两种颜色的小球的数目相同. 小明从布袋中 随机摸出1个球, 记下颜色后放回布袋中, 摇匀后再随机摸出1个球, 记下颜 色后放回布袋中……如此进行大量重复摸球试验后, 小明发现摸出红色小 球的频率稳定于20%, 由此可以估计布袋中的黑色小球有________个. 8分析 设黑色小球有x个, 则黑、白两种颜色的小球一共有2x个. ∵经过多次试验后发现摸到红色小球的频率稳定于20%, ∴可估计摸到 红色小球的概率为20%, ∴4=20%(4+2x), 解得x=8, ∴黑色小球有8个.相关题 在一个不透明的布袋中装 有若干个只有颜色不同的 小球, 如果袋中有红球5个, 黄球4个, 其余为白球, 从袋 子中随机摸出1个球, “摸出黄球”的概率为 , 那么袋中白球的个数为( ).
A.2 B.3
C.4 D.12B中考链接母题1 事件类型的判别(教材P134习题25.1第 1题)
请指出在下列事件中, 哪些是随机事件, 哪些 是必然事件, 哪些是不可能事件. (1)通常温度降到0 ℃以下, 纯净的水结冰; (2)随意翻到一本书的某页, 这页的页码是奇数; (3)从地面发射1枚导弹, 未击中空中目标;(4)明天 太阳从东方升起;(5)汽车累积行驶10 000 km, 从 未出现故障;(6)购买1张彩票, 中奖. 考点:随机事件、必然事件、不可能事件的 概念.
考情:随机事件、必然事件、不可能事件的判 别是常考知识点.
策略:根据三种事件的概念解题, 在一定条件下, 判断哪些事件必然会发生, 哪些事件必然不会发 生, 哪些事件可能发生也可能不发生. 链接1 [漳州中考]下列事件中, 属于必然事件 的是( ).
A.打开电视机, 正在播广告
B.打开数学书, 恰好翻到第50页
C.抛掷一枚质地均匀的硬币, 恰好正面朝上
D.一天有24小时 D母题2 概率计算公式(教材P134习题25.1第4题) 一个质地均匀的小正方体, 六个面分别标有数 字“1”“1”“2”“4”“5”“5”. 掷小正方体后, 观 察朝上一面的数字.
(1)出现“5”的概率是多少?
(2)出现“6”的概率是多少?
(3)出现奇数的概率是多少?考点:概率的计算公式P(A)= .
考情:概率的计算是中考的热点, 近年来还出 现了概率与几何图形、函数、统计等相结合的 试题.
策略:根据所给的条件, 列举所有可能的结果和 事件A包含的可能的结果, 进而利用概率的计算 公式进行计算. 链接2 [攀枝花中考]布袋中装有除颜色外没 有其他区别的1个红球和2个白球, 搅匀后从中摸出 1个球, 放回搅匀, 再摸出1个球, 两次都摸出白球的 概率是( ).
A母题3 与几何有关的概率(教材P134习题25.1第 5题) 如图25-Z-10是一个可以自由转 动的质地均匀的转盘, 被分成12个相 同的扇形. 请你在转盘的适当地方涂 上红、蓝两种颜色, 使得转动的转盘 停止时, 指针指向红、蓝两色的概
率分别为考点:概率的计算公式P= , 几何图形的面积公 式与几何图形的有关性质.
考情:概率与几何的结合是中考的常考考点, 题 型以填空题、选择题为主.
策略:把求概率问题转化为求几何图形的面积 比或者几何图形性质的分类讨论问题或几何计 数问题. 链接3 [山西中考]小江 玩投掷飞镖的游戏, 他设计 了一个如图25-Z-11所示的 靶子, E, F分别是矩形ABCD 的边AD, BC上的点, 且EF∥AB, M, N是EF上的任 意两点, 则投掷一次, 飞镖落在阴影部分的概率是 ( ). C分析 ∵矩形ABFE内阴影部分的面积= × 矩形ABFE的面积, 矩形DCFE内阴影部分的面积= ×矩形DCFE的面积,
∴阴影部分的面积= ×矩形ABCD的面积,
∴飞镖落在阴影部分的概率是 . 故选C. 母题4 用列表法或画树状图法求概率(教材P138练 习第2题) 有6张看上去无差别的卡片, 上面分别写着1, 2, 3, 4, 5, 6. 随机抽取1张后, 放回并混在一起, 再随 机抽取1张, 那么第二次取出的数字能够整除第一 次取出的数字的概率是多少?考点:概率的计算公式P= .
考情:利用列表法或画树状图法求概率是中考 的热点, 常见的考查方式是求某一事件的概率.
策略:利用列表法或画树状图法求概率. 链接4 [无锡中考](1)甲、乙、丙、丁四人做 传球游戏:第一次由甲将球随机传给乙、丙、丁 中的某一人, 从第二次起, 每一次都由持球者将球 再随机传给其他三人中的某一人. 求第二次传球后 球回到甲手里的概率(请用画树状图或列表的方法 给出分析过程).
(2)如果甲和另外n(n≥2)个人做(1)中同样的 游戏, 那么第三次传球后球回到甲手里的概率是______(请直接写结果). 解 (1)画树状图如图25-Z-12. ∵共有9种等可能的结果, 其 中符合要求的结果有3种, ∴P(第二次传球后球回到甲 手里)=
(2)∵第三次传球的结果 总数是n3, 传给甲的结果数是 n(n-1),
∴第三次传球后球回到甲手里的概率是
故答案为
母题5 判断游戏的公平性(教材P153复习题25第 8题)
同学们, 你们都知道“石头、剪子、布”的游 戏吧!如果两个人做这种游戏, 随机出手一次, 两 个人获胜的概率各是多少?考点:概率的计算, 用列表法或画树状图法求事 件的概率.
考情:利用概率判断游戏的公平性是中考的热点.
策略:看一个游戏是否公平, 只要看游戏双方赢 的机会是否相同, 如果相同, 那么游戏公平;如 果不相同, 那么游戏不公平, 要使游戏变得公平, 就要修改它的规则. 链接5 [广州中考]在一个不透明的口袋里装 有分别标有数字2, 4, 6的3个小球(小球除数字不同 外其余都相同), 另有3张背面完全一样、正面分别 写有数字6, 7, 8的卡片. 现从口袋中任意摸出1个 小球, 再从这3张背面朝上的卡片中任意摸出1张 卡片. (1)请你用列表或画树状图的方法, 表示出所 有可能出现的结果; (2)小红和小莉做游戏, 制定了两个游戏 规则: 规则1:若两次摸出的数字至少有一次是 “6”, 则小红赢;否则小莉赢. 规则2:若摸出的卡片上的数字是球上数字的 整数倍, 则小红赢;否则小莉赢. 小红要想在游戏中获胜, 她应选择哪一种规 则?并说明理由. 解 (1)列表如下:
(2)小红应选择规则1. 理由: 规则1:P(小红赢)= ;规则2:P(小红 赢)= . ∵ , ∴小红应选择规则1.
谢 谢 观 看!
同课章节目录
