人教版九年级数学上册第二十二章 二次函数章末复习课件(共68张)
文档属性
| 名称 | 人教版九年级数学上册第二十二章 二次函数章末复习课件(共68张) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-24 00:00:00 | ||
图片预览





文档简介
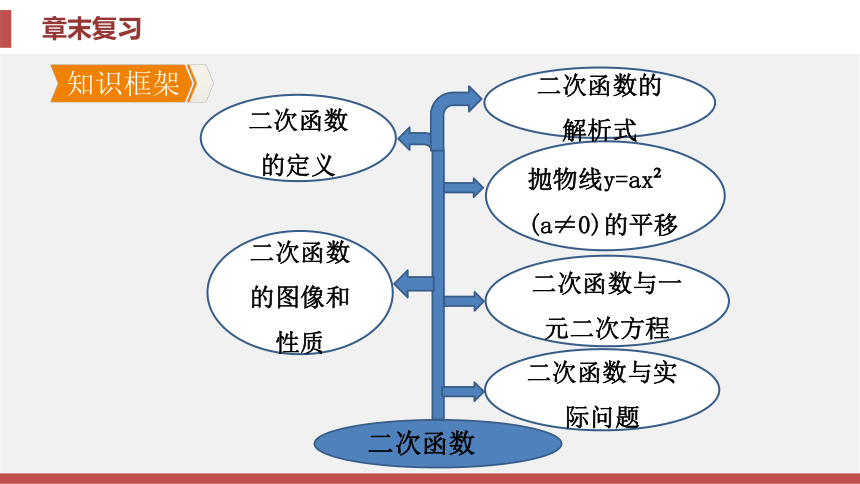
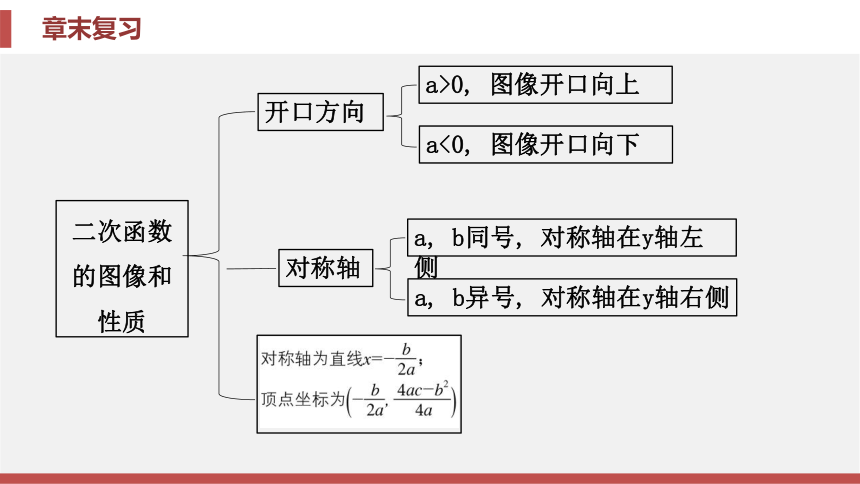
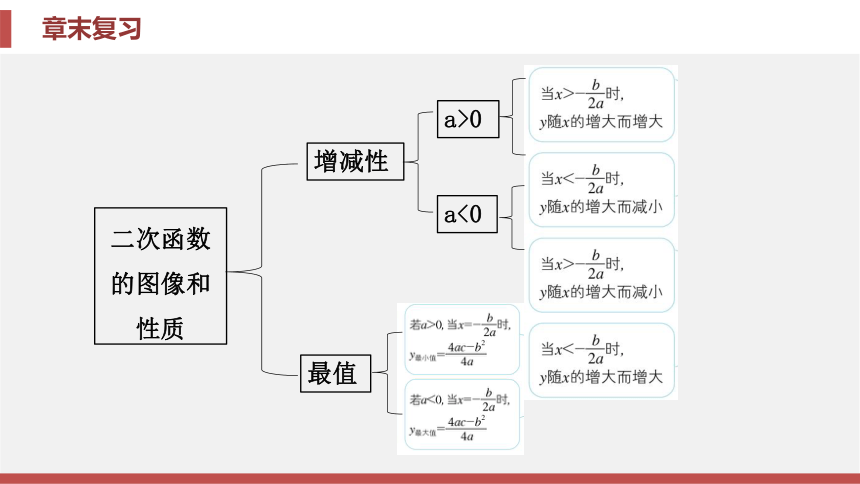
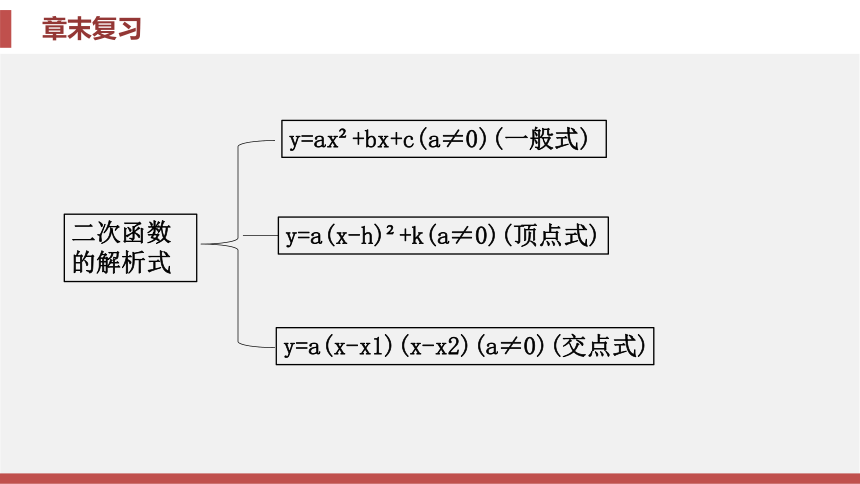
课件68张PPT。第二十二章 二次函数章末复习第二十二章 二次函数章末复习二次函数的定义形如y=ax2+bx+c(a, b, c是常数, a≠0)开口方向烦烦烦鬼鬼鬼鬼鬼鬼鬼鬼跟鬼鬼鬼鬼鬼g鬼鬼a>0, 图像开口向上a<0, 图像开口向下对称轴a, b同号, 对称轴在y轴左侧a, b异号, 对称轴在y轴右侧增减性最值a>0a<0y=ax2+bx+c(a≠0)(一般式)y=a(x-x1)(x-x2)(a≠0)(交点式)二次函数
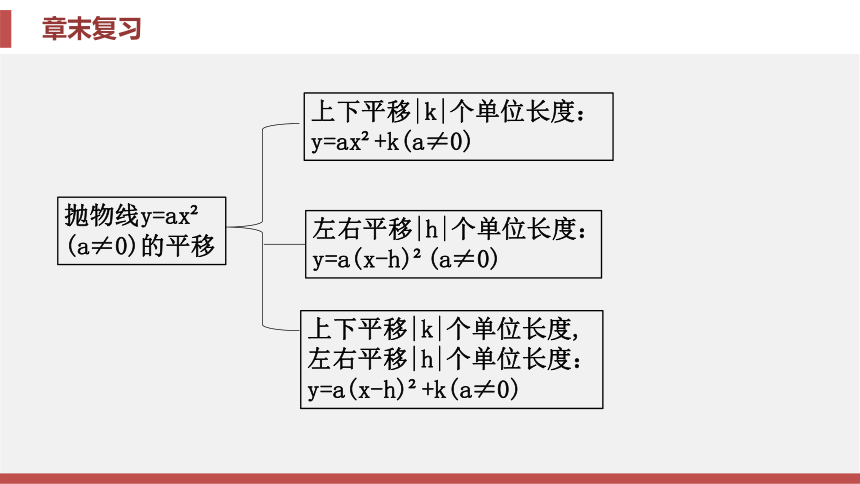
的解析式y=a(x-h)2+k(a≠0)(顶点式)上下平移|k|个单位长度:
y=ax2+k(a≠0)上下平移|k|个单位长度,
左右平移|h|个单位长度:
y=a(x-h)2+k(a≠0)抛物线y=ax2
(a≠0)的平移左右平移|h|个单位长度:
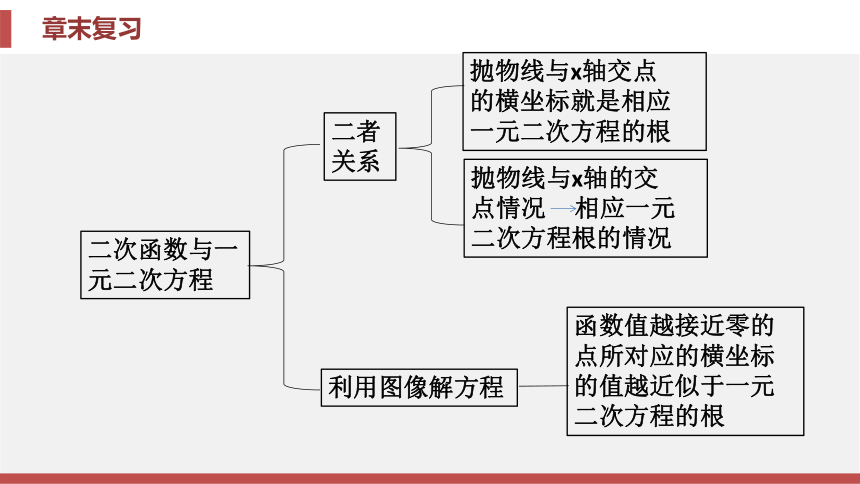
y=a(x-h)2(a≠0)二者
关系利用图像解方程抛物线与x轴交点
的横坐标就是相应
一元二次方程的根函数值越接近零的
点所对应的横坐标
的值越近似于一元
二次方程的根抛物线与x轴的交
点情况 相应一元
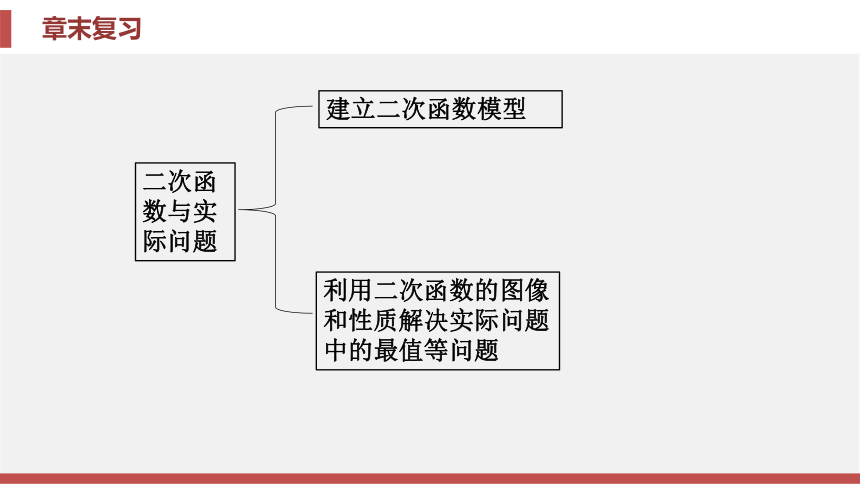
二次方程根的情况二次函
数与实
际问题建立二次函数模型利用二次函数的图像和性质解决实际问题中的最值等问题【要点指导】二次函数y=ax2+bx+c(a≠0)的图像与a, b, c的关系: (1)a的值与图像的开口方向有关, 图像开口向上时, a>0;图像开口向下 时, a<0.
(2)当对称轴在y轴左侧时, a, b同号;当对称轴在y轴右侧时, a, b 异号.
(3)图像与y轴的交点在y轴正半轴上时, c>0;图像与y轴的交点是 原点时, c=0;图像与y轴的交点在y轴负半轴上时, c<0. 专题一 二次函数的图像与系数的关系(4)当图像与x轴 有两个交点时, b2-4ac>0;当图像与x轴只有一个交点时, b2-4ac=0; 当图像与x轴没有交点时, b2-4ac<0.
(5)图像过点(1, a+b+c)和点(-1, a-b+c), 再根据图像上的点的位置可确定式子a+b+c和a-b+c的符号. B分析 D解析 因为图像开口向下,所以a<0.因为图像的对称轴在y轴的右侧,所以a,b异号,所以b>0.因为图像与y轴的交点在y轴的正半轴上,所以c>0.因为图像与x轴有两个交点,所以b2-4ac>0.故选D.【要点指导】利用待定系数法求二次函数的解析式时, 可以根据所 给出的条件设出不同的解析式:①一般式y=ax2+bx+c(a≠0), 当已知条 件是三个普通点时, 可选择一般式;②顶点式y=a(x-h)2+k(a≠0), 当已 知条件是顶点和一个普通点时, 可选择顶点式;③交点式y=a(x-x1)· (x-x2)(a≠0), 其中x1, x2是抛物线与x轴交点的横坐标, 当已知条件是抛物 线与x轴的两个交点及一个普通点时, 可选择交点式.专题二 用待定系数法求二次函数的解析式例2 已知二次函数的图像以A(-1, 4)为顶点, 且过点B(2, -5).
(1)求该函数的解析式;
(2)求该函数图像与坐标轴的交点坐标.相关题2 已知抛物线与x轴的交点是 A(-2, 0), B(1, 0), 且经过点 C(2, 8).
(1)求该抛物线所对应的函 数解析式;
(2) 求该抛 物线的顶点 坐标.【要点指导】二次函数y=ax2+bx+c的图像与x轴的位置关系有三 种:没有公共点、有一个公共点、有两个公共点, 这分别对应着一元二 次方程ax2+bx+c=0的根的三种情况:没有实数根、有两个相等的实数 根、有两个不相等的实数根. 专题三 二次函数与一元二次方程的关系 例3 若二次函数y=2(k-1)x2-4kx+2(k-1)的图像与x轴有两个不同的 交点, 求k的取值范围. B专题四 二次函数图像的平移和轴对称变换 【要点指导】研究二次函数的图像的平移、轴对称变换过程, 实际 就是确定变换后所得图像的二次函数解析式, 研究变换后的图像和性质 的过程, 关键是找到变换后图像上的特殊点(如抛物线的顶点), 从而得出 函数解析式, 最后利用二次函数的性质解答. C专题五 二次函数与三角形或四边形的综合题【要点指导】解答二次函数与三角形或四边形的综合题, 必须在充 分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的条件, 在 复杂的“背景”下辨认、分解基本图形或通过添加辅助线补全或构造 基本图形, 并善于联想所学知识, 突破思维障碍, 合理运用方程等数学思 想才能解决. 专题六 二次函数的实际应用【要点指导】运用建模思想, 将实际问题中的信息语言转化成数学 语言, 抽象、归纳出其中的数量关系, 从而运用二次函数的有关知识加以 解决.(2)现有一辆载有救援物资 的货车从甲地出发需经过 此桥开往乙地, 已知甲地距 此桥280 km(桥长忽略不 计). 货车正以每小时40 km 的速度开往乙地, 当行驶 1小时时, 忽然接到紧急通 知:前方连降暴雨, 造成水 位以每小时0.25 m的速度 持续上涨(货车接到通知 时水位在CD处, 当水位 达到桥拱最高点O时, 禁止 车辆通行), 如果货车按原 来的速度行驶, 那么能否 安全通过此桥?若能, 请 说明理由;若不能, 要使货 车安全通过此桥, 货车的 速度应至少为每小时多少 千米?
【要点指导】生活中变量之间存在相互依存和相互对应的关系, 函 数就是刻画变量之间关系的数学模型, 所以, 对于存在相互依存关系的图 形规律问题, 可建立函数模型, 利用函数来解答.专题 用函数思想解决规律性问题n2+2n分析 分析题意可得到下表:
把表中的图形次序及其对应的黑色棋子个数分别作为点的横坐标、纵 坐标, 可得(1, 3), (2, 8), (3, 15), (4, 24), …, 将这些点在平面直角坐标系中描 出, 观察图中描出的点的整体分布, 它们均在一条抛物线附近, 所以假设摆放 第n个图形需要y个黑色棋子, 则y与n之间存在y=an2+bn+c(a≠0)的函数关系. 将(1, 3), (2, 8), (3, 15)代入y=an2+bn+c, 相关题 观察图22-Z-10中正六边 形网的变化规律:
(1)完成下表:
(2)如果用n表示正六边形 网的圈数, m表示这个正多 边形中小点的总数, 那么 如何用含n的代数式表示 m?解:(1)填表如下:
(2)将正六边形网的圈数和小点总数分别作为点的横坐标、纵坐标,可得(1,6),(2,18),(3,36),(4,60),(5,90).将上述各点在平面直角坐标系中描出.考点:二次函数的图像与性质.
考情:涉及二次函数图像间平移的考题多以选择 题、填空题的形式出现, 有时还与配方法等知识 综合考查. 利用二次函数的增减性结合图像求最 值、比较函数值的大小是中考的热点.
策略:(1)二次函数图像的平移规律:“左加右 减, 上加下减”. (2)二次函数y=a(x-h)2+k(a≠0) 的图像的顶点坐标为(h, k), 对称轴为直线x=h, 当 a>0时, 图像开口向上, 当a<0时, 图像开口向下.链接1 [肇庆中考]二次函数y=x2+2x-5有 ( ).
A.最大值-5 B.最小值-5
C.最大值-6 D.最小值-6DD分析 A.∵抛物线开口向下, ∴a<0. ∵抛物线与y轴的交点在正半轴上, ∴c>0, ∴ac<0, 故此选项错误.
B.∵抛物线与x轴有2个交点, ∴b2-4ac>0, 故此选项错误.
C.∵抛物线y=ax2+bx+c交x轴于点(-1, 0)和 (4, 0), ∴对称轴是直线x=1.5, 故此选项错误.
D.∵抛物线的对称轴在y轴右侧, ∴a, b异号. 而a<0, ∴b>0, 故此选项正确. 故选D. 母题2 二次函数与一元二次方程的关系(教材 P47习题22.2第5题)
画出函数y=x2-2x-3的图像, 利用图像回答:
(1)方程x2-2x-3=0的解是什么;
(2)x取什么值时, 函数值大于0;
(3)x取什么值时, 函数值小于0.考点:二次函数与一元二次方程或不等式之间 的关系.
考情:利用二次函数的图像求一元二次方程的根 或不等式的解集. 策略:求二次函数的图像与x轴的交点的横坐标, 就是求当y=0时对应一元二次方程的根;利用二 次函数的图像求不等式的解集, 即求函数中满足 条件的y值对应的x的取值范围.
链接3 [江西中考]已知二次函数y=x2+bx-2 的图像与x轴的一个交点坐标为(1, 0), 则它与x轴的 另一个交点坐标是( ).
A.(1, 0) B.(2, 0)
C.(-2, 0) D.(-1, 0) C母题3 二次函数的应用(教材P52习题22.3第8题)
某宾馆有50个房间供游客居住. 当每个房间 每天的定价为180元时, 房间会全部住满;当每个 房间每天的定价每增加10元时, 就会有一个房间 空闲. 如果游客居住房间, 宾馆需对每个房间每天 支出20元的各种费用. 房价定为多少时, 宾馆利润 最大?考点:二次函数的实际应用.
考情:二次函数的应用常与时事背景、地方特 色、一次函数图像相结合, 作为常考题型出现.
策略:(1)销售利润=每件商品利润×销售量; (2)求函数的最值.
链接5 [徐州中考]某网店以每件60元的价格 购进一批商品, 若以单价80元/件销售, 则每月可售 出300件. 经调查表明:该商品每件每上涨1元, 每 月的销售量就减少10件.
(1)请你写出每月销售该商品的利润y(元)与单 价x(元/件)之间的函数解析式;
(2)当单价定为多少元/件时, 每月销售该商品 的利润最大?最大利润为多少? 解 (1)y=(x-60)[300-10(x-80)]
=(x-60)(300-10x+800)
=(x-60)(1100-10x)
=-10x2+1700x-66 000,
即y=-10x2+1700x-66 000(80≤x≤110).
(2)y=-10x2+1700x-66 000=-10(x-85)2+6250.
因为a=-10<0, 所以当x=85时, y有最大值, 最大 值为6250.
即当单价定为85元/件时, 每月销售该商品的 利润最大, 最大利润为6250元.
谢 谢 观 看!
的解析式y=a(x-h)2+k(a≠0)(顶点式)上下平移|k|个单位长度:
y=ax2+k(a≠0)上下平移|k|个单位长度,
左右平移|h|个单位长度:
y=a(x-h)2+k(a≠0)抛物线y=ax2
(a≠0)的平移左右平移|h|个单位长度:
y=a(x-h)2(a≠0)二者
关系利用图像解方程抛物线与x轴交点
的横坐标就是相应
一元二次方程的根函数值越接近零的
点所对应的横坐标
的值越近似于一元
二次方程的根抛物线与x轴的交
点情况 相应一元
二次方程根的情况二次函
数与实
际问题建立二次函数模型利用二次函数的图像和性质解决实际问题中的最值等问题【要点指导】二次函数y=ax2+bx+c(a≠0)的图像与a, b, c的关系: (1)a的值与图像的开口方向有关, 图像开口向上时, a>0;图像开口向下 时, a<0.
(2)当对称轴在y轴左侧时, a, b同号;当对称轴在y轴右侧时, a, b 异号.
(3)图像与y轴的交点在y轴正半轴上时, c>0;图像与y轴的交点是 原点时, c=0;图像与y轴的交点在y轴负半轴上时, c<0. 专题一 二次函数的图像与系数的关系(4)当图像与x轴 有两个交点时, b2-4ac>0;当图像与x轴只有一个交点时, b2-4ac=0; 当图像与x轴没有交点时, b2-4ac<0.
(5)图像过点(1, a+b+c)和点(-1, a-b+c), 再根据图像上的点的位置可确定式子a+b+c和a-b+c的符号. B分析 D解析 因为图像开口向下,所以a<0.因为图像的对称轴在y轴的右侧,所以a,b异号,所以b>0.因为图像与y轴的交点在y轴的正半轴上,所以c>0.因为图像与x轴有两个交点,所以b2-4ac>0.故选D.【要点指导】利用待定系数法求二次函数的解析式时, 可以根据所 给出的条件设出不同的解析式:①一般式y=ax2+bx+c(a≠0), 当已知条 件是三个普通点时, 可选择一般式;②顶点式y=a(x-h)2+k(a≠0), 当已 知条件是顶点和一个普通点时, 可选择顶点式;③交点式y=a(x-x1)· (x-x2)(a≠0), 其中x1, x2是抛物线与x轴交点的横坐标, 当已知条件是抛物 线与x轴的两个交点及一个普通点时, 可选择交点式.专题二 用待定系数法求二次函数的解析式例2 已知二次函数的图像以A(-1, 4)为顶点, 且过点B(2, -5).
(1)求该函数的解析式;
(2)求该函数图像与坐标轴的交点坐标.相关题2 已知抛物线与x轴的交点是 A(-2, 0), B(1, 0), 且经过点 C(2, 8).
(1)求该抛物线所对应的函 数解析式;
(2) 求该抛 物线的顶点 坐标.【要点指导】二次函数y=ax2+bx+c的图像与x轴的位置关系有三 种:没有公共点、有一个公共点、有两个公共点, 这分别对应着一元二 次方程ax2+bx+c=0的根的三种情况:没有实数根、有两个相等的实数 根、有两个不相等的实数根. 专题三 二次函数与一元二次方程的关系 例3 若二次函数y=2(k-1)x2-4kx+2(k-1)的图像与x轴有两个不同的 交点, 求k的取值范围. B专题四 二次函数图像的平移和轴对称变换 【要点指导】研究二次函数的图像的平移、轴对称变换过程, 实际 就是确定变换后所得图像的二次函数解析式, 研究变换后的图像和性质 的过程, 关键是找到变换后图像上的特殊点(如抛物线的顶点), 从而得出 函数解析式, 最后利用二次函数的性质解答. C专题五 二次函数与三角形或四边形的综合题【要点指导】解答二次函数与三角形或四边形的综合题, 必须在充 分利用几何图形的性质及题设的基础上挖掘几何图形中隐含的条件, 在 复杂的“背景”下辨认、分解基本图形或通过添加辅助线补全或构造 基本图形, 并善于联想所学知识, 突破思维障碍, 合理运用方程等数学思 想才能解决. 专题六 二次函数的实际应用【要点指导】运用建模思想, 将实际问题中的信息语言转化成数学 语言, 抽象、归纳出其中的数量关系, 从而运用二次函数的有关知识加以 解决.(2)现有一辆载有救援物资 的货车从甲地出发需经过 此桥开往乙地, 已知甲地距 此桥280 km(桥长忽略不 计). 货车正以每小时40 km 的速度开往乙地, 当行驶 1小时时, 忽然接到紧急通 知:前方连降暴雨, 造成水 位以每小时0.25 m的速度 持续上涨(货车接到通知 时水位在CD处, 当水位 达到桥拱最高点O时, 禁止 车辆通行), 如果货车按原 来的速度行驶, 那么能否 安全通过此桥?若能, 请 说明理由;若不能, 要使货 车安全通过此桥, 货车的 速度应至少为每小时多少 千米?
【要点指导】生活中变量之间存在相互依存和相互对应的关系, 函 数就是刻画变量之间关系的数学模型, 所以, 对于存在相互依存关系的图 形规律问题, 可建立函数模型, 利用函数来解答.专题 用函数思想解决规律性问题n2+2n分析 分析题意可得到下表:
把表中的图形次序及其对应的黑色棋子个数分别作为点的横坐标、纵 坐标, 可得(1, 3), (2, 8), (3, 15), (4, 24), …, 将这些点在平面直角坐标系中描 出, 观察图中描出的点的整体分布, 它们均在一条抛物线附近, 所以假设摆放 第n个图形需要y个黑色棋子, 则y与n之间存在y=an2+bn+c(a≠0)的函数关系. 将(1, 3), (2, 8), (3, 15)代入y=an2+bn+c, 相关题 观察图22-Z-10中正六边 形网的变化规律:
(1)完成下表:
(2)如果用n表示正六边形 网的圈数, m表示这个正多 边形中小点的总数, 那么 如何用含n的代数式表示 m?解:(1)填表如下:
(2)将正六边形网的圈数和小点总数分别作为点的横坐标、纵坐标,可得(1,6),(2,18),(3,36),(4,60),(5,90).将上述各点在平面直角坐标系中描出.考点:二次函数的图像与性质.
考情:涉及二次函数图像间平移的考题多以选择 题、填空题的形式出现, 有时还与配方法等知识 综合考查. 利用二次函数的增减性结合图像求最 值、比较函数值的大小是中考的热点.
策略:(1)二次函数图像的平移规律:“左加右 减, 上加下减”. (2)二次函数y=a(x-h)2+k(a≠0) 的图像的顶点坐标为(h, k), 对称轴为直线x=h, 当 a>0时, 图像开口向上, 当a<0时, 图像开口向下.链接1 [肇庆中考]二次函数y=x2+2x-5有 ( ).
A.最大值-5 B.最小值-5
C.最大值-6 D.最小值-6DD分析 A.∵抛物线开口向下, ∴a<0. ∵抛物线与y轴的交点在正半轴上, ∴c>0, ∴ac<0, 故此选项错误.
B.∵抛物线与x轴有2个交点, ∴b2-4ac>0, 故此选项错误.
C.∵抛物线y=ax2+bx+c交x轴于点(-1, 0)和 (4, 0), ∴对称轴是直线x=1.5, 故此选项错误.
D.∵抛物线的对称轴在y轴右侧, ∴a, b异号. 而a<0, ∴b>0, 故此选项正确. 故选D. 母题2 二次函数与一元二次方程的关系(教材 P47习题22.2第5题)
画出函数y=x2-2x-3的图像, 利用图像回答:
(1)方程x2-2x-3=0的解是什么;
(2)x取什么值时, 函数值大于0;
(3)x取什么值时, 函数值小于0.考点:二次函数与一元二次方程或不等式之间 的关系.
考情:利用二次函数的图像求一元二次方程的根 或不等式的解集. 策略:求二次函数的图像与x轴的交点的横坐标, 就是求当y=0时对应一元二次方程的根;利用二 次函数的图像求不等式的解集, 即求函数中满足 条件的y值对应的x的取值范围.
链接3 [江西中考]已知二次函数y=x2+bx-2 的图像与x轴的一个交点坐标为(1, 0), 则它与x轴的 另一个交点坐标是( ).
A.(1, 0) B.(2, 0)
C.(-2, 0) D.(-1, 0) C母题3 二次函数的应用(教材P52习题22.3第8题)
某宾馆有50个房间供游客居住. 当每个房间 每天的定价为180元时, 房间会全部住满;当每个 房间每天的定价每增加10元时, 就会有一个房间 空闲. 如果游客居住房间, 宾馆需对每个房间每天 支出20元的各种费用. 房价定为多少时, 宾馆利润 最大?考点:二次函数的实际应用.
考情:二次函数的应用常与时事背景、地方特 色、一次函数图像相结合, 作为常考题型出现.
策略:(1)销售利润=每件商品利润×销售量; (2)求函数的最值.
链接5 [徐州中考]某网店以每件60元的价格 购进一批商品, 若以单价80元/件销售, 则每月可售 出300件. 经调查表明:该商品每件每上涨1元, 每 月的销售量就减少10件.
(1)请你写出每月销售该商品的利润y(元)与单 价x(元/件)之间的函数解析式;
(2)当单价定为多少元/件时, 每月销售该商品 的利润最大?最大利润为多少? 解 (1)y=(x-60)[300-10(x-80)]
=(x-60)(300-10x+800)
=(x-60)(1100-10x)
=-10x2+1700x-66 000,
即y=-10x2+1700x-66 000(80≤x≤110).
(2)y=-10x2+1700x-66 000=-10(x-85)2+6250.
因为a=-10<0, 所以当x=85时, y有最大值, 最大 值为6250.
即当单价定为85元/件时, 每月销售该商品的 利润最大, 最大利润为6250元.
谢 谢 观 看!
同课章节目录
