人教版高一数学必修一第三章3.1.1《方程的根与函数的零点》课件
文档属性
| 名称 | 人教版高一数学必修一第三章3.1.1《方程的根与函数的零点》课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 998.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 00:00:00 | ||
图片预览





文档简介
课件19张PPT。方程的根与函数的零点
判断下列方程是否有根,有几个实数根?分别是多少?方程函数函
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点方程的根就是相应函数图像与
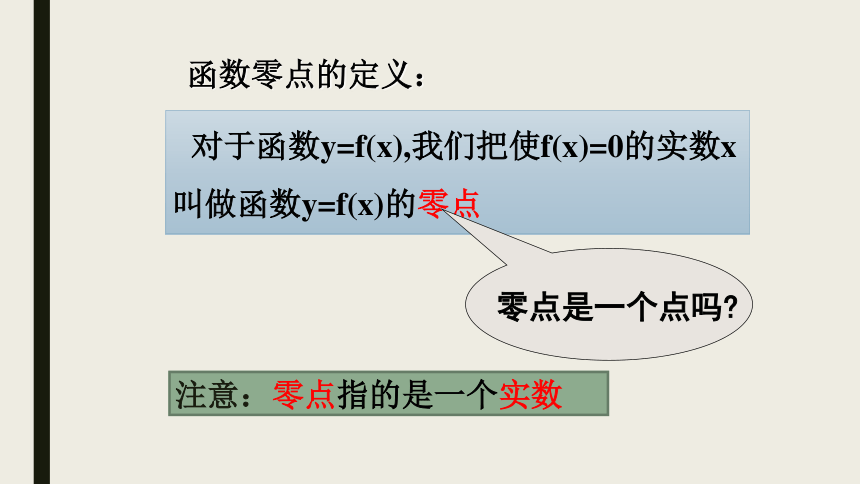
x轴交点的横坐标x2-2x+1=0y= x2-2x-3y= x2-2x+1x2-2x-3=0y= x2-2x+3x2-2x+3=0 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点函数零点的定义:注意:零点指的是一个实数方程是否有根相应的函数是否有零点转化求方程根的问题求相应函数的零
点问题的问题转化函数y=f(x)有零点方程f(x)=0有实数根函数y=f(x)的图象与x轴
有交点.等价关系求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点例1:求函数 的零点 求下列函数的零点:
(1) ;(2) .
练习2.已知函数 的定义域为R的奇函数,且 在 有一个零点,则
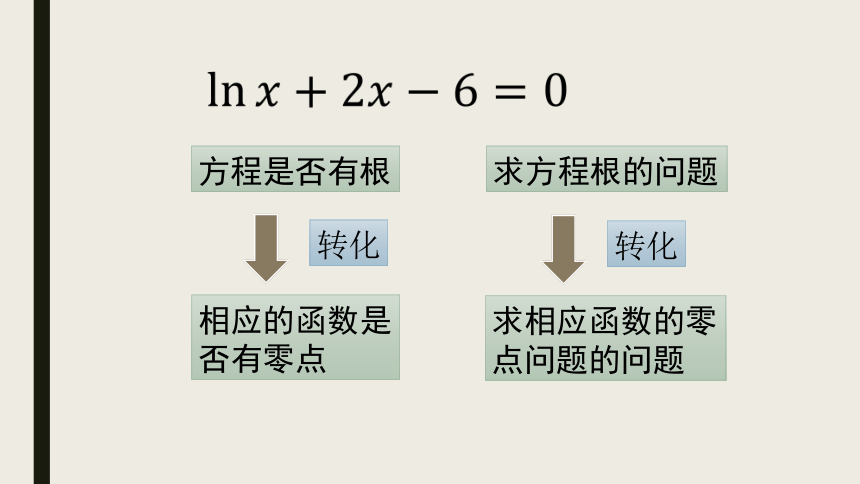
的零点个数为_____练习 方程 是否有实根?有几个实根? 思考探究?????如果函数 y=f(x)在区间[a, b]上的图象是连续不断
的一条曲线,并且有f(a)·f(b)<0, 那么, 函数y=f(x) 在区
间(a, b)内有零点, 即存在c∈(a, b),使f(c)=0, 这个c也
就是方程f(x) = 0的根.
零点存在定理:问题1: 函数f(x)在区间(a,b)上有f(a)f(b)<0,那么函数f(x)在区间(a,b)上是否一定存在零点,请举例说明。 问题2: 函数f(x)在区间(a,b)上有f(a)f(b)<0,且有零点,那么一定只有一个吗?请举例说明。概念反思问题3: 函数y=f(x) 在区间(a, b)内有零点,一定有f(a)·f(b)<0吗?唯一零点的存在性定理 已知函数 的图像是连续不断的,有 如下表所对应值:
那么函数 在区间 上的零点至少有_____个 3例2由上表可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内有零点。 又因为函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点。解:分别列出部分x、f(x)的对应值表如下:例3 求函数f(x)=lnx+2x-6的零点个数。且f(x)在(0,+∞)单调递增。练习 对于函数y=f(x), 叫做函数
y=f(x)的零点。方程f(x)=0有实数根函数的零点定义:等价关系使f(x)=0的实数x
小 结 谢谢!
数
的
图
象方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点方程的根就是相应函数图像与
x轴交点的横坐标x2-2x+1=0y= x2-2x-3y= x2-2x+1x2-2x-3=0y= x2-2x+3x2-2x+3=0 对于函数y=f(x),我们把使f(x)=0的实数x叫做函数y=f(x)的零点函数零点的定义:注意:零点指的是一个实数方程是否有根相应的函数是否有零点转化求方程根的问题求相应函数的零
点问题的问题转化函数y=f(x)有零点方程f(x)=0有实数根函数y=f(x)的图象与x轴
有交点.等价关系求函数零点的步骤:
(1)令f(x)=0;
(2)解方程f(x)=0;
(3)写出零点例1:求函数 的零点 求下列函数的零点:
(1) ;(2) .
练习2.已知函数 的定义域为R的奇函数,且 在 有一个零点,则
的零点个数为_____练习 方程 是否有实根?有几个实根? 思考探究?????如果函数 y=f(x)在区间[a, b]上的图象是连续不断
的一条曲线,并且有f(a)·f(b)<0, 那么, 函数y=f(x) 在区
间(a, b)内有零点, 即存在c∈(a, b),使f(c)=0, 这个c也
就是方程f(x) = 0的根.
零点存在定理:问题1: 函数f(x)在区间(a,b)上有f(a)f(b)<0,那么函数f(x)在区间(a,b)上是否一定存在零点,请举例说明。 问题2: 函数f(x)在区间(a,b)上有f(a)f(b)<0,且有零点,那么一定只有一个吗?请举例说明。概念反思问题3: 函数y=f(x) 在区间(a, b)内有零点,一定有f(a)·f(b)<0吗?唯一零点的存在性定理 已知函数 的图像是连续不断的,有 如下表所对应值:
那么函数 在区间 上的零点至少有_____个 3例2由上表可知f(2)<0,f(3)>0,即f(2)·f(3)<0,说明这个函数在区间(2,3)内有零点。 又因为函数f(x)在定义域(0,+∞)内是增函数,所以它仅有一个零点。解:分别列出部分x、f(x)的对应值表如下:例3 求函数f(x)=lnx+2x-6的零点个数。且f(x)在(0,+∞)单调递增。练习 对于函数y=f(x), 叫做函数
y=f(x)的零点。方程f(x)=0有实数根函数的零点定义:等价关系使f(x)=0的实数x
小 结 谢谢!
