人教版八年级数学上册第十三章 轴对称 13.3.2等边三角形课件(共21张PPT)
文档属性
| 名称 | 人教版八年级数学上册第十三章 轴对称 13.3.2等边三角形课件(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 152.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-03 12:36:11 | ||
图片预览




文档简介
课件21张PPT。13.3.2等边三角形如图 △ABC中AB=AC
等腰三角形的性质:
1、等腰三角形两底角相等(等边对等角),
2、等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(三线合一)。
3、等腰三角形是轴对称图形.对称轴______________所在直线.回顾旧知2.如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).∴AB=AC (等角对等边 )∵ △ABC中, ∠B=?C等腰三角形的判定:回顾旧知1.有两条边相等的三角形是等腰三角形;1.了解等边三角形与等腰三角形的关系.并掌握等边三角形的性质;
2.掌握等边三角形的判定方法,会判断一个三角形是等边三角形;
3.能灵活运用等边三角形的性质与判定解决相关的几何问题. 在等腰三角形中,有一种特殊的等腰三角形——三条边都相等的三角形,叫等边三角形观察思考:1.如图,作为等腰三角形的等边三角形,
具有哪些性质?
等边三角形又有哪些特殊的性质呢?
2.一个三角形满足什么条件就是等边三角形?提示:
根据等腰三角形的性质去探讨等边三角形的性质:
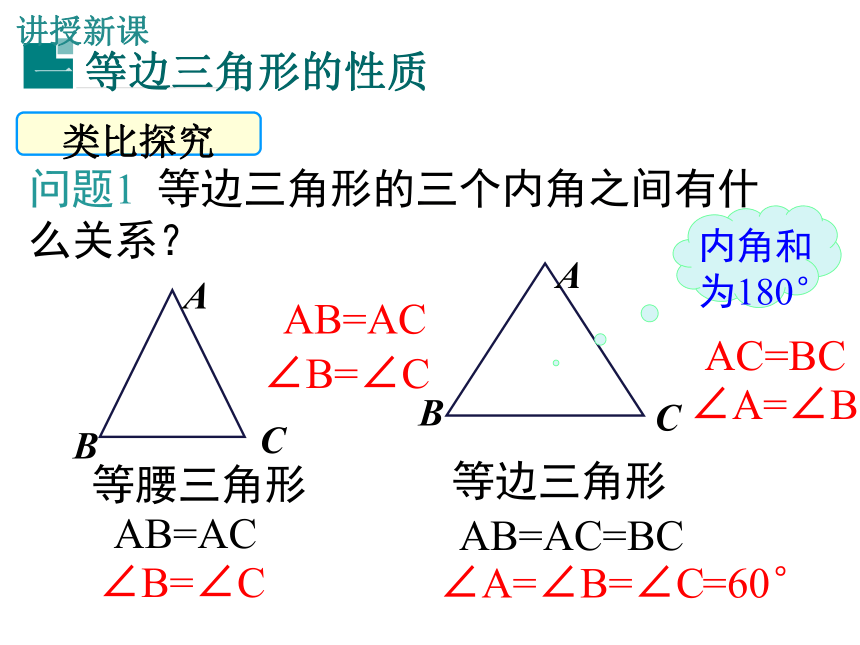
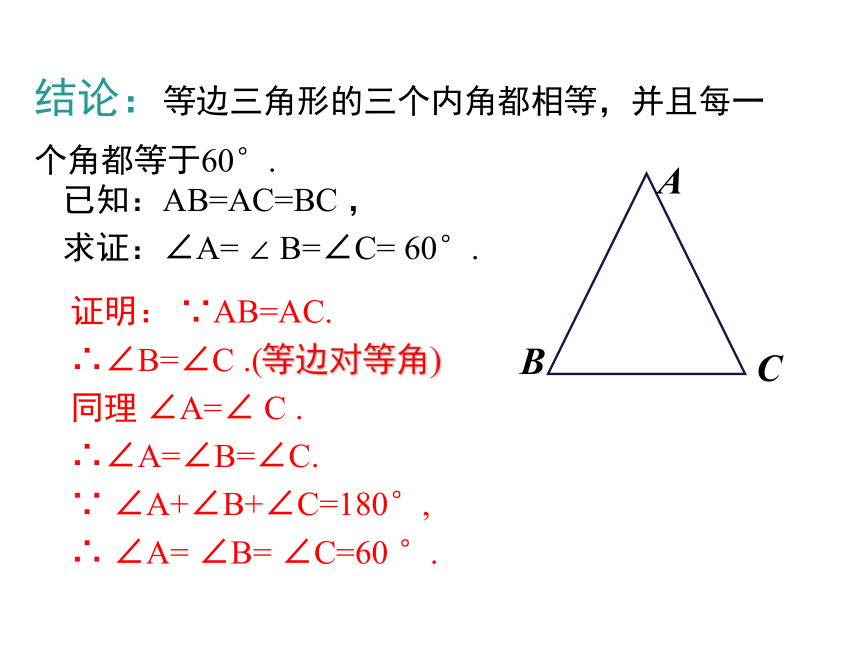
①从边看;②从角看;③从对称性看;④从重要线段看讲授新课类比探究问题1 等边三角形的三个内角之间有什么关系?等腰三角形AB=AC∠B=∠C等边三角形AB=AC=BCAB=AC∠B=∠CAC=BC∠A=∠B∠A=∠B=∠C=60°结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°. 证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠ C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
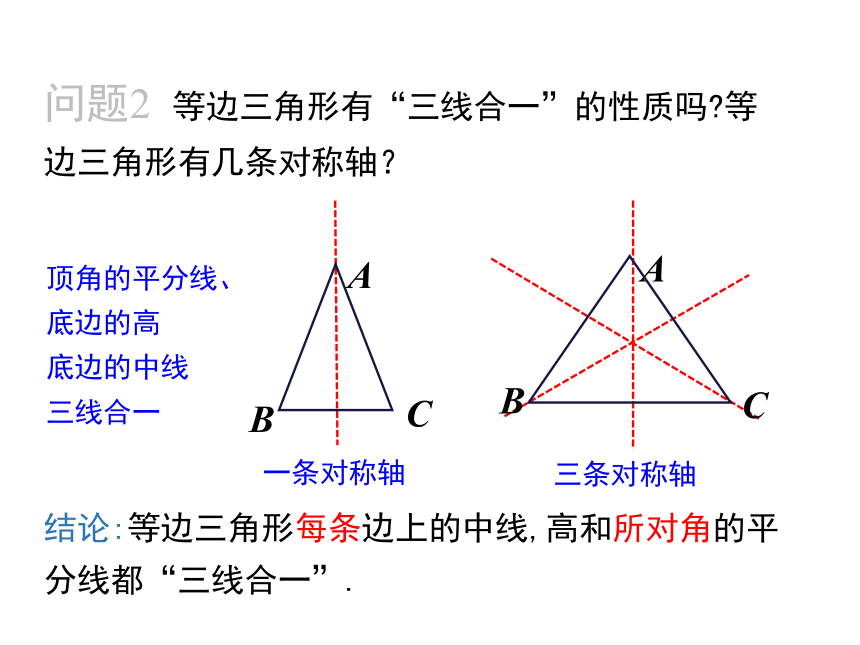
问题2 等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.顶角的平分线、底边的高
底边的中线
三线合一一条对称轴三条对称轴每一边上的中线、高和这一边所对的角的平分线互相重合三个角都相等,
对称轴(3条)等边三角形对称轴(1条)两个底角相等底边上的中线、高和顶角的平分线互相重合且都是60o两条边相等三条边都相等知识要点思考题?一个三角形满足什么条件
就是等边三角形? 1.三条边都相等的三角形是等边三角形2.三个角都相等的三角形是等边三角形 3.有一个角是60°的等腰三角形是等边三角形类比探究三个角都相等的三角形是等边三角形
等边三角形从角看:两个角相等的三角形是等腰三角形从边看:两条边相等的三角形是等腰三角形三条边都相等的三角形是等边三角形小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形等边三角形的判定:
1.三条边都相等的三角形是等边三角形
2.三个角都相等的三角形是等边三角形 3.有一个角是60°的三角形是等边三角形∵ ∠A= 60°,AB=AC
∴△ABC是等边三角形∵ ∠A= 60°,AB=BC
∴△ABC是等边三角形2.三个角都相等的三角形是等边三角形.3.有一个角是60°的等腰三角形是等边三角形.1.三边都相等的三角形是等边三角形.(定义)一般三角形等腰三角形ABC等边三角形的判定方法1.下列三角形是等边三角形的是 。
①有两个角是60度的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个角是60度的等腰三角形。2.一个三角形任意一边上的高都是这边上的中线,则这个三角形是 。①②④等边三角形例4 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.典例精析证明:∵ △ABC是等边三角形,∴ ∠A= ∠B= ∠C.∵ DE//BC,∴ ∠ADE= ∠B, ∠ AED= ∠C.∴ ∠A= ∠ADE= ∠ AED.∴ △ADE是等边三角形.想一想:本题还有其他证法吗? 证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.变式1 若点D、E 在边AB、AC 的延长线上,且
DE∥BC,结论还成立吗? 变式2 若点D、E 在边AB、AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.4变式 . 等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.深层探究,合作交流5.如图, △ABC是等边三角形,分别延长AB,BC,CA到D,E,F,使BD=CE=AF,连接DE,EF,FD.
求证: △DEF是等边三角形.证明:∵ △ABC是等边三角形
∴∠1=∠2=60°,AB=AC
∵∠1+∠3=∠2+∠4=180°
∴∠3=∠4
∵BD=AF
∴BD+AB=AF+AC
即AD=CF
在△ADF和△CFE中, ∴DF=EF,∠5=∠6
AD=CF ∴∠5+∠7=∠6+∠7
∠3=∠4 =∠1=60°
AF=CE ∴△DEF是等边三角形
∴ △ADF≌CFE(SAS) 5. 如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.我们这节课学习了哪些知识?
谈谈你的体会.
等腰三角形的性质:
1、等腰三角形两底角相等(等边对等角),
2、等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(三线合一)。
3、等腰三角形是轴对称图形.对称轴______________所在直线.回顾旧知2.如果一个三角形有两个角相等,那么这两个角所对的边也相等(简写成“等角对等边”).∴AB=AC (等角对等边 )∵ △ABC中, ∠B=?C等腰三角形的判定:回顾旧知1.有两条边相等的三角形是等腰三角形;1.了解等边三角形与等腰三角形的关系.并掌握等边三角形的性质;
2.掌握等边三角形的判定方法,会判断一个三角形是等边三角形;
3.能灵活运用等边三角形的性质与判定解决相关的几何问题. 在等腰三角形中,有一种特殊的等腰三角形——三条边都相等的三角形,叫等边三角形观察思考:1.如图,作为等腰三角形的等边三角形,
具有哪些性质?
等边三角形又有哪些特殊的性质呢?
2.一个三角形满足什么条件就是等边三角形?提示:
根据等腰三角形的性质去探讨等边三角形的性质:
①从边看;②从角看;③从对称性看;④从重要线段看讲授新课类比探究问题1 等边三角形的三个内角之间有什么关系?等腰三角形AB=AC∠B=∠C等边三角形AB=AC=BCAB=AC∠B=∠CAC=BC∠A=∠B∠A=∠B=∠C=60°结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°. 证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠ C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
问题2 等边三角形有“三线合一”的性质吗?等边三角形有几条对称轴?结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.顶角的平分线、底边的高
底边的中线
三线合一一条对称轴三条对称轴每一边上的中线、高和这一边所对的角的平分线互相重合三个角都相等,
对称轴(3条)等边三角形对称轴(1条)两个底角相等底边上的中线、高和顶角的平分线互相重合且都是60o两条边相等三条边都相等知识要点思考题?一个三角形满足什么条件
就是等边三角形? 1.三条边都相等的三角形是等边三角形2.三个角都相等的三角形是等边三角形 3.有一个角是60°的等腰三角形是等边三角形类比探究三个角都相等的三角形是等边三角形
等边三角形从角看:两个角相等的三角形是等腰三角形从边看:两条边相等的三角形是等腰三角形三条边都相等的三角形是等边三角形小明认为还有第三种方法“两条边相等且有一个角是60°的三角形也是等边三角形”,你同意吗?等边三角形的判定方法:
有一个角是60°的等腰三角形是等边三角形.∵ ∠A= ∠ B= ∠ C
∴△ABC是等边三角形等边三角形的判定:
1.三条边都相等的三角形是等边三角形
2.三个角都相等的三角形是等边三角形 3.有一个角是60°的三角形是等边三角形∵ ∠A= 60°,AB=AC
∴△ABC是等边三角形∵ ∠A= 60°,AB=BC
∴△ABC是等边三角形2.三个角都相等的三角形是等边三角形.3.有一个角是60°的等腰三角形是等边三角形.1.三边都相等的三角形是等边三角形.(定义)一般三角形等腰三角形ABC等边三角形的判定方法1.下列三角形是等边三角形的是 。
①有两个角是60度的三角形;
②三个外角都相等的三角形;
③一边上的高也是这边上的中线的三角形;
④有一个角是60度的等腰三角形。2.一个三角形任意一边上的高都是这边上的中线,则这个三角形是 。①②④等边三角形例4 如图,在等边三角形ABC中,DE∥BC,
求证:△ADE是等边三角形.典例精析证明:∵ △ABC是等边三角形,∴ ∠A= ∠B= ∠C.∵ DE//BC,∴ ∠ADE= ∠B, ∠ AED= ∠C.∴ ∠A= ∠ADE= ∠ AED.∴ △ADE是等边三角形.想一想:本题还有其他证法吗? 证明:∵ △ABC 是等边三角形,
∴ ∠A =∠ABC =∠ACB =60°.
∵ DE∥BC,
∴ ∠ABC =∠ADE,
∠ACB =∠AED.
∴ ∠A =∠ADE =∠AED.
∴ △ADE 是等边三角形.变式1 若点D、E 在边AB、AC 的延长线上,且
DE∥BC,结论还成立吗? 变式2 若点D、E 在边AB、AC 的反向延长线上,
且DE∥BC,结论依然成立吗? 证明: ∵ △ABC 是等边三角形,
∴ ∠BAC =∠B =∠C =60°.
∵ DE∥BC,
∴ ∠B =∠D,∠C =∠E.
∴ ∠EAD =∠D =∠E.
∴ △ADE 是等边三角形.4变式 . 等边△ABC中,点P在△ABC内,点Q在△ABC外,且∠ABP=∠ACQ,BP=CQ,问△APQ是什么形状的三角形?试证明你的结论.解:△APQ为等边三角形.
证明如下:∵△ABC为等边三角形,
∴AB=AC.
∵BP=CQ,∠ABP=∠ACQ,
∴△ABP≌△ACQ(SAS),
∴AP=AQ,∠BAP=∠CAQ.
∵∠BAC=∠BAP+∠PAC=60°,
∴∠PAQ=∠CAQ+∠PAC=60°,
∴△APQ是等边三角形.深层探究,合作交流5.如图, △ABC是等边三角形,分别延长AB,BC,CA到D,E,F,使BD=CE=AF,连接DE,EF,FD.
求证: △DEF是等边三角形.证明:∵ △ABC是等边三角形
∴∠1=∠2=60°,AB=AC
∵∠1+∠3=∠2+∠4=180°
∴∠3=∠4
∵BD=AF
∴BD+AB=AF+AC
即AD=CF
在△ADF和△CFE中, ∴DF=EF,∠5=∠6
AD=CF ∴∠5+∠7=∠6+∠7
∠3=∠4 =∠1=60°
AF=CE ∴△DEF是等边三角形
∴ △ADF≌CFE(SAS) 5. 如图,等边△ABC中,D、E、F分别是各边上的一点,且AD=BE=CF.
求证:△DEF是等边三角形.证明:∵△ABC为等边三角形,且AD=BE=CF
∴AF=BD=CE,∠A=∠B=∠C=60°,
∴△ADF≌△BED≌△CFE(SAS),
∴DF=ED=EF,
∴△DEF是等边三角形.我们这节课学习了哪些知识?
谈谈你的体会.
