江西省南昌市洪都中学2019-2020学年高二上学期第三次联考 文数试题(PDF版)
文档属性
| 名称 | 江西省南昌市洪都中学2019-2020学年高二上学期第三次联考 文数试题(PDF版) |

|
|
| 格式 | zip | ||
| 文件大小 | 776.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 00:00:00 | ||
图片预览

文档简介
1
2021 届高二年级第三次联考
文科数学试题
考试用时:120 分钟 满分分值:150 分 2019 年 9 月 26 日
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.已知直线 l1:ax ? 3y ?1? 0与直线 l2:6x ? 4y ?3 ? 0垂直,则 a的值为( )
A.2 B.
9
2
C.﹣2 D.
9
2
?
2.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
3.如图所示是水平放置三角形的直观图,点 D是△ABC的 BC边中点,AB,BC分别与 y′
轴、x′轴平行,则三条线段 AB,AD,AC中( )
A.最长的是 AB,最短的是 AC
B.最长的是 AC,最短的是 AB
C.最长的是 AB,最短的是 AD
D.最长的是 AC,最短的是 AD
4.已知向量a?与b
?
的夹角为120?, 3a ?
?
, | | 13a b? ?
??
,则 | |b ?
?
( )
A.1 B.3 C.4 D.5
5.设 m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若α∥β,α∥γ,则β∥γ;②若α⊥β,m∥α,则 m⊥β;
③若 m⊥α,m∥β,则α⊥β;④若 m∥n,n?α,则 m∥α.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
6.若将函数 ? ? 2sin 1
6
f x x ?? ?? ? ?? ?
? ?
的图象上各点横坐标缩短到原来的
1
2
(纵坐标不变)得到
函数 ? ?g x 的图象,则下列说法正确的是( )
A.函数 ? ?g x 在 0 6
?? ?
? ?
? ?
, 上单调递增 B.函数 ? ?g x 的周期是
2
?
C.函数 ? ?g x 的图象关于点 012
?? ??? ?
? ?
, 对称 D.函数 ? ?g x 在 0 6
?? ?
? ?
? ?
, 上最大值是 1
7.已知正三棱柱 1 1 1ABC ABC? 的底面边长为 1,侧棱长为 2, E为 1AA 的中点,从 E拉一
条绳子绕过侧棱 1CC 到达 B点的最短绳长为( )
A. 2 B. 3 C. 5 D. 6
8.如图所示是一几何体的三视图,正视图是一等腰直角三角形,且斜边 BD长为 2,侧视
图是一直角三角形,俯视图为一直角梯形,且 1AB BC? ? ,则异面直线 PB与CD所成角
的正切值是( )
A.1 B. 2 C. 1
2
D. 2
2
8.已知直线 y x m? ? ? 与曲线 2 2y x x? ? ? 有两个不同交点,
则( )
A. 0 2 1m? ? ? B. 0 2 1m? ? ?
C. 2 1 2 1m? ? ? ? ? D. 0 2 1m? ? ?
10.如图,在四面体 D-ABC中,若 AB=CB,AD=CD,
E是 AC的中点,则下列正确的是( )
A.平面 ABC?平面 ABD
B.平面 ABD?平面 BDC
C.平面 ABC?平面 BDE,且平面 ADC?平面 BDE
D.平面 ABC?平面 ADC,且平面 ADC?平面 BDE
11.已知 0m ? , 0xy ? ,当 2x y? ? 时,不等式
2 4m
x y
? ? 恒成立,则m的取值范围是
A. ?2,? ??? B.? ?2,?? C. ?0, 2 ?? D. ? ?0,2
12.如图,正方体 AC1的棱长为 1,过点 A作平面 A1BD的垂线,垂足为点 H,以下四个命题:
①点 H是△A1BD的垂心;
②AH垂直平面 CB1D1
③直线 AH和 BB1所成角为 45°;
④AH的延长线经过点C1
其中正确命题的个数为( )
A.0 B.1 C.2 D.3
二、填空题(本题共 4 小题,每小题 5 分,共 20 分.把答案填在题中的横线上)
13.已知等差数列{ }na 的前n项和为 nS ,若 5 7 9 15a a a? ? ? ,则 13S ? ________.
14.已知实数 ,x y满足约束条件
0
4 0
1
x y
x y
y
? ??
? ? ? ??
? ??
,则 2z x y? ? ? 的最大值是 .
15.圆 2 21 : 4 3 0C x y x? ? ? ? 与圆
2 2
2 : ( 1) ( 4)C x y a? ? ? ? 恰有三条公切线,则实数 a的值
是 .
16.在三棱锥 S ?ABC中,△ABC是边长为 4 的正三角形,SA=SB=SC
=10,平面 DEFH分别与 AB,BC,SC,SA交于 D,E,F,H,
且 D,E分别是 AB,BC的中点,如果直线 SB∥平面 DEFH,那
么四边形 DEFH的面积为 .
2
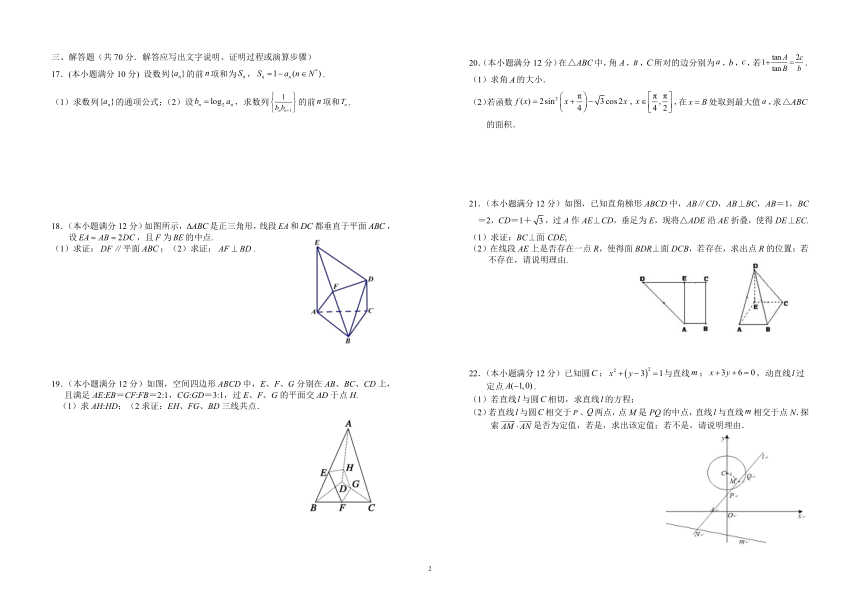
三、解答题(共 70 分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 10 分) 设数列{ }na 的前n项和为 nS , *1 ( )n nS a n N? ? ? .
(1)求数列{ }na 的通项公式;(2)设 2logn nb a? ,求数列
1
1
n nb b ?
? ?
? ?
? ?
的前n项和 nT .
18.(本小题满分 12 分)如图所示, ABC? 是正三角形,线段 EA和DC都垂直于平面 ABC,
设 2EA AB DC? ? ,且F为 BE的中点.
(1)求证:DF∥平面 ABC;(2)求证: AF BD? .
19.(本小题满分 12 分)如图,空间四边形 ABCD中,E、F、G分别在 AB、BC、CD上,
且满足 AE:EB=CF:FB=2:1,CG:GD=3:1,过 E、F、G的平面交 AD于点 H.
(1)求 AH:HD;(2 求证:EH、FG、BD三线共点.
20.(本小题满分 12 分)在 ABC△ 中,角 A,B,C所对的边分别为 a,b,c,若
tan 21
tan
A c
B b
? ? .
(1)求角 A的大小.
(2)若函数 2
π( ) 2sin 3 cos 2
4
f x x x? ?? ? ?? ?
? ?
,
π π,
4 2
x ? ?? ? ?? ?
,在 x B? 处取到最大值 a,求 ABC△
的面积.
21.(本小题满分 12 分)如图,已知直角梯形 ABCD中,AB∥CD,AB⊥BC,AB=1,BC
=2,CD=1+ 3 ,过 A作 AE⊥CD,垂足为 E,现将△ADE沿 AE折叠,使得 DE⊥EC.
(1)求证:BC⊥面 CDE;
(2)在线段 AE上是否存在一点 R,使得面 BDR⊥面 DCB,若存在,求出点 R的位置;若
不存在,请说明理由.
22.(本小题满分 12 分)已知圆C: ? ?22 3 1x y? ? ? 与直线m: 3 6 0x y? ? ? ,动直线 l过
定点 ( 1,0)A ? .
(1)若直线 l与圆C相切,求直线 l的方程;
(2)若直线 l与圆C相交于 P、Q两点,点 M是 PQ的中点,直线 l与直线m相交于点 N.探
索 AM AN?
????? ????
是否为定值,若是,求出该定值;若不是,请说明理由.
1
文科数学参考答案
一、选择题
CDBCA ACDAC BD
二、填空题
13.65 14.?1 15.16 16.10
三、解答题
17.(1)因为 Sn ?1? an ?n?N * ?,所以 Sn?1 ?1?an?1( n?N *,且 n ? 2),
则 Sn ? Sn?1 ? ?1? an ?? ?1? an?1 ?( n?N *,且n ? 2)
即 an ?
1
2
an?1( n?N *,且n ? 2) .………………………………2分
因为 Sn ?1? an ?n?N * ?,所以 S1 ?1? a1 ? a1,即 1 12a ? .………………………3分
所以? ?na 是以
1
2
为首项,
1
2
为公比的等比数列.
故 ? ?*12
n
na n N
? ?? ?? ?
? ?
.. . ………………………………5分
(2) 2logn nb a? ,所以 2
1log
2
n
nb n
? ?? ? ?? ?
? ?
. .. . ………………………………6分
所以 ? ?1
1 1 1 1
1 1n nb b n n n n?
? ? ?
? ? , .. . ………………………………8分
故
1 1 11
2 2 3n
T ? ? ? ?? ? ? ? ? ?? ? ? ?
? ? ? ?
? 1 1 11
1 1 1
n
n n n n
? ?? ? ? ?? ?? ? ?? ?
. ………………10分
18.(1)证明:如图所示,取 AB的中点G ,连接 ,CG FG .
∵ ,EF FB AG GB? ? ,∴ .. . ………………………………2分
又 ∴ ∴四边形CDFG为平行四边形. 故DF CG? .……4分
∵DF ?平面 ABC ,CG ?平面 ABC ,∴DF ?平面 ABC ……………………..5分
(2)证明:∵ EA ?平面 ABC ,∴ .AE CG? 又 ABC? 是正三角形,∴ .CG AB?
∴CG ?平面 .AEB .. . ………………………………7分
又∵DF CG? ,∴DF ?平面 AEB .∴ .AF DF? …………………………9分
∵ ,AE AB EF FB? ? ,∴ .AF BE? ∴ AF ?平面 BED ,………………………11分
∴ .AF BD? ...………………………………12分
19. (1)∵AE
EB
=
CF
FB
=2,∴EF∥AC,
∴EF∥平面 ACD,而 EF?平面 EFGH, ...………………………………2分
平面 EFGH∩平面 ACD=GH,
∴EF∥GH,∴AC∥GH. ...………………………………4分
∴
AH
HD
=
CG
GD
=3,∴AH:HD=3:1. ...………………………………6分
(2)证明:∵EF∥GH,且EF
AC
=
1
3
,
GH
AC
=
1
4
,
∴EF≠GH,∴四边形 EFGH为梯形. ...………………………………8分
令 EH∩FG=P,则 P∈EH,而 EH?平面 ABD,
又 P∈FG,FG?平面 BCD, ...………………………………10分
平面 ABD∩平面 BCD=BD,
∴P∈BD,∴EH、FG、BD三线共点. .....……………………………12分
20.解:(1)∵
sin cos 2sin1
cos sin sin
A B C
A B B
? ? ? , .....……………………………1分
∴
cos sin sin cos 2sin
cos sin sin
A B A B C
A B B
?
? ,∴
sin( ) 2sin
cos sin sin
A B C
A B B
?
? ,……………………………3分
∴
sin 2sin
cos
C C
A
? ,又∵ sin 0C ? ,∴
1cos
2
A ? ,故
π
3
A ? .…………………………5分
(2)∵ ? ? 2 π π2sin 3cos2 1 2sin 2
4 3
f x x x x? ? ? ?? ? ? ? ? ?? ? ? ?
? ? ? ?
,…………………………7分
∴当
π π2
3 2
x ? ? ,即
5π
12
x ? 时, ? ?max 3f x ? ,此时
5π
12
B ? ,
π
4
C ? , 3a ? , ……9分
∵
sin sin
a c
A C
? ,∴
723sin 2 673sin
2
a cC
A
?
? ? ? , …………………………10分
则
1 1 6 2 9 3 3sin 3 6
2 2 4 4
S ac B ? ?? ? ? ? ? ? . …………………………12分
21.(1)∵AE⊥CD,∴AE⊥CE,AE⊥DE,
又CE DE E?? , AE? ?平面CDE. …………………………3分
由已知易得 AE∥BC,∴BC⊥平面 CDE; ………………………5分
2
(2)存在,当R点满足
1
4
AR AE? 时,面BDR ?面BDC.………………………6分
证明:如图,过点 E作 EF⊥CD交 CD于 F,易得
1
4
CF CD? ,…………………7分
由(1)可知 BC⊥平面 CDE ,则 BC⊥EF,∴EF⊥平面 BCD,…………………9分
过点 F作 FG∥BC交 BD于 G,连结 GR,则
3
4
FG BC? ,
又
1
4
AR AE? ,且 BC∥AE,∴四边形 EFGR是平行四边形, ………………11分
∴EF∥GR,∴GR⊥平面 BCD,又GR ?平面 BDR,面 BDR ?面BDC.…………12分
22.解:(1)当直线 l的斜率不存在时,直线 l的方程为 1x ? ? ,
此时与圆相切,符合题意; ………………………………1分
当直线 l的斜率存在时,设直线 l的方程为 ( 1)y k x? ? ,即 0kx y k? ? ? ,
若直线与圆相切,则圆心 (0,3) 到直线的距离等于半径 1,
所以
2
3
1
1
k
k
? ?
?
?
,解得
4
3
k ? ,
所以直线 l的方程为
4 ( 1)
3
y x? ? ,即 4 3 4 0x y? ? ? . ………………………………4分
综上,直线 l的方程为 1x ? ? 或 4 3 4 0x y? ? ? .
直线 l的方程为 1x ? ? 或 4 3 4 0x y? ? ? . ………………………………5分
(2)∵CM⊥MN,∴ ( ) = + =AM AN AC CM AC AN CM AC AN AN NA? ? ? ? ? ? ?
????? ???? ???? ????? ???? ???? ??? ????? ?? ??? ?? ? ? ????
若直线 l与 x轴垂直时,不符合题意; ………………………………7分
所以 l的斜率存在,设直线 l的方程为 ( 1)y k x? ? ,
则由
3 6
( 1) 1 3
3 6 0 5
1 3
kxy k x k
x y ky
k
? ?? ??? ?? ? ??? ?? ? ? ?? ? ?
? ??
,即
3 6 5( , )
1 3 1 3
k kN
k k
? ? ?
? ?
. ………………………9分
∴
5 5( , )
1 3 1 3
kAN
k k
? ?
?
? ?
????
,从而
5 15 5
1 3
=
1 3
=AN AN kAM AC
k k
? ?
? ? ? ? ?
? ?
???? ????? ?? ? ?????
.
综上所述, = 5AAM N ??
??? ??????
. ………………………12分
2021 届高二年级第三次联考
文科数学试题
考试用时:120 分钟 满分分值:150 分 2019 年 9 月 26 日
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只
有一项是符合题目要求的)
1.已知直线 l1:ax ? 3y ?1? 0与直线 l2:6x ? 4y ?3 ? 0垂直,则 a的值为( )
A.2 B.
9
2
C.﹣2 D.
9
2
?
2.一个几何体的三视图如图所示,则该几何体的直观图可以是( )
3.如图所示是水平放置三角形的直观图,点 D是△ABC的 BC边中点,AB,BC分别与 y′
轴、x′轴平行,则三条线段 AB,AD,AC中( )
A.最长的是 AB,最短的是 AC
B.最长的是 AC,最短的是 AB
C.最长的是 AB,最短的是 AD
D.最长的是 AC,最短的是 AD
4.已知向量a?与b
?
的夹角为120?, 3a ?
?
, | | 13a b? ?
??
,则 | |b ?
?
( )
A.1 B.3 C.4 D.5
5.设 m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:
①若α∥β,α∥γ,则β∥γ;②若α⊥β,m∥α,则 m⊥β;
③若 m⊥α,m∥β,则α⊥β;④若 m∥n,n?α,则 m∥α.
其中正确命题的序号是( )
A.①③ B.①④ C.②③ D.②④
6.若将函数 ? ? 2sin 1
6
f x x ?? ?? ? ?? ?
? ?
的图象上各点横坐标缩短到原来的
1
2
(纵坐标不变)得到
函数 ? ?g x 的图象,则下列说法正确的是( )
A.函数 ? ?g x 在 0 6
?? ?
? ?
? ?
, 上单调递增 B.函数 ? ?g x 的周期是
2
?
C.函数 ? ?g x 的图象关于点 012
?? ??? ?
? ?
, 对称 D.函数 ? ?g x 在 0 6
?? ?
? ?
? ?
, 上最大值是 1
7.已知正三棱柱 1 1 1ABC ABC? 的底面边长为 1,侧棱长为 2, E为 1AA 的中点,从 E拉一
条绳子绕过侧棱 1CC 到达 B点的最短绳长为( )
A. 2 B. 3 C. 5 D. 6
8.如图所示是一几何体的三视图,正视图是一等腰直角三角形,且斜边 BD长为 2,侧视
图是一直角三角形,俯视图为一直角梯形,且 1AB BC? ? ,则异面直线 PB与CD所成角
的正切值是( )
A.1 B. 2 C. 1
2
D. 2
2
8.已知直线 y x m? ? ? 与曲线 2 2y x x? ? ? 有两个不同交点,
则( )
A. 0 2 1m? ? ? B. 0 2 1m? ? ?
C. 2 1 2 1m? ? ? ? ? D. 0 2 1m? ? ?
10.如图,在四面体 D-ABC中,若 AB=CB,AD=CD,
E是 AC的中点,则下列正确的是( )
A.平面 ABC?平面 ABD
B.平面 ABD?平面 BDC
C.平面 ABC?平面 BDE,且平面 ADC?平面 BDE
D.平面 ABC?平面 ADC,且平面 ADC?平面 BDE
11.已知 0m ? , 0xy ? ,当 2x y? ? 时,不等式
2 4m
x y
? ? 恒成立,则m的取值范围是
A. ?2,? ??? B.? ?2,?? C. ?0, 2 ?? D. ? ?0,2
12.如图,正方体 AC1的棱长为 1,过点 A作平面 A1BD的垂线,垂足为点 H,以下四个命题:
①点 H是△A1BD的垂心;
②AH垂直平面 CB1D1
③直线 AH和 BB1所成角为 45°;
④AH的延长线经过点C1
其中正确命题的个数为( )
A.0 B.1 C.2 D.3
二、填空题(本题共 4 小题,每小题 5 分,共 20 分.把答案填在题中的横线上)
13.已知等差数列{ }na 的前n项和为 nS ,若 5 7 9 15a a a? ? ? ,则 13S ? ________.
14.已知实数 ,x y满足约束条件
0
4 0
1
x y
x y
y
? ??
? ? ? ??
? ??
,则 2z x y? ? ? 的最大值是 .
15.圆 2 21 : 4 3 0C x y x? ? ? ? 与圆
2 2
2 : ( 1) ( 4)C x y a? ? ? ? 恰有三条公切线,则实数 a的值
是 .
16.在三棱锥 S ?ABC中,△ABC是边长为 4 的正三角形,SA=SB=SC
=10,平面 DEFH分别与 AB,BC,SC,SA交于 D,E,F,H,
且 D,E分别是 AB,BC的中点,如果直线 SB∥平面 DEFH,那
么四边形 DEFH的面积为 .
2
三、解答题(共 70 分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分 10 分) 设数列{ }na 的前n项和为 nS , *1 ( )n nS a n N? ? ? .
(1)求数列{ }na 的通项公式;(2)设 2logn nb a? ,求数列
1
1
n nb b ?
? ?
? ?
? ?
的前n项和 nT .
18.(本小题满分 12 分)如图所示, ABC? 是正三角形,线段 EA和DC都垂直于平面 ABC,
设 2EA AB DC? ? ,且F为 BE的中点.
(1)求证:DF∥平面 ABC;(2)求证: AF BD? .
19.(本小题满分 12 分)如图,空间四边形 ABCD中,E、F、G分别在 AB、BC、CD上,
且满足 AE:EB=CF:FB=2:1,CG:GD=3:1,过 E、F、G的平面交 AD于点 H.
(1)求 AH:HD;(2 求证:EH、FG、BD三线共点.
20.(本小题满分 12 分)在 ABC△ 中,角 A,B,C所对的边分别为 a,b,c,若
tan 21
tan
A c
B b
? ? .
(1)求角 A的大小.
(2)若函数 2
π( ) 2sin 3 cos 2
4
f x x x? ?? ? ?? ?
? ?
,
π π,
4 2
x ? ?? ? ?? ?
,在 x B? 处取到最大值 a,求 ABC△
的面积.
21.(本小题满分 12 分)如图,已知直角梯形 ABCD中,AB∥CD,AB⊥BC,AB=1,BC
=2,CD=1+ 3 ,过 A作 AE⊥CD,垂足为 E,现将△ADE沿 AE折叠,使得 DE⊥EC.
(1)求证:BC⊥面 CDE;
(2)在线段 AE上是否存在一点 R,使得面 BDR⊥面 DCB,若存在,求出点 R的位置;若
不存在,请说明理由.
22.(本小题满分 12 分)已知圆C: ? ?22 3 1x y? ? ? 与直线m: 3 6 0x y? ? ? ,动直线 l过
定点 ( 1,0)A ? .
(1)若直线 l与圆C相切,求直线 l的方程;
(2)若直线 l与圆C相交于 P、Q两点,点 M是 PQ的中点,直线 l与直线m相交于点 N.探
索 AM AN?
????? ????
是否为定值,若是,求出该定值;若不是,请说明理由.
1
文科数学参考答案
一、选择题
CDBCA ACDAC BD
二、填空题
13.65 14.?1 15.16 16.10
三、解答题
17.(1)因为 Sn ?1? an ?n?N * ?,所以 Sn?1 ?1?an?1( n?N *,且 n ? 2),
则 Sn ? Sn?1 ? ?1? an ?? ?1? an?1 ?( n?N *,且n ? 2)
即 an ?
1
2
an?1( n?N *,且n ? 2) .………………………………2分
因为 Sn ?1? an ?n?N * ?,所以 S1 ?1? a1 ? a1,即 1 12a ? .………………………3分
所以? ?na 是以
1
2
为首项,
1
2
为公比的等比数列.
故 ? ?*12
n
na n N
? ?? ?? ?
? ?
.. . ………………………………5分
(2) 2logn nb a? ,所以 2
1log
2
n
nb n
? ?? ? ?? ?
? ?
. .. . ………………………………6分
所以 ? ?1
1 1 1 1
1 1n nb b n n n n?
? ? ?
? ? , .. . ………………………………8分
故
1 1 11
2 2 3n
T ? ? ? ?? ? ? ? ? ?? ? ? ?
? ? ? ?
? 1 1 11
1 1 1
n
n n n n
? ?? ? ? ?? ?? ? ?? ?
. ………………10分
18.(1)证明:如图所示,取 AB的中点G ,连接 ,CG FG .
∵ ,EF FB AG GB? ? ,∴ .. . ………………………………2分
又 ∴ ∴四边形CDFG为平行四边形. 故DF CG? .……4分
∵DF ?平面 ABC ,CG ?平面 ABC ,∴DF ?平面 ABC ……………………..5分
(2)证明:∵ EA ?平面 ABC ,∴ .AE CG? 又 ABC? 是正三角形,∴ .CG AB?
∴CG ?平面 .AEB .. . ………………………………7分
又∵DF CG? ,∴DF ?平面 AEB .∴ .AF DF? …………………………9分
∵ ,AE AB EF FB? ? ,∴ .AF BE? ∴ AF ?平面 BED ,………………………11分
∴ .AF BD? ...………………………………12分
19. (1)∵AE
EB
=
CF
FB
=2,∴EF∥AC,
∴EF∥平面 ACD,而 EF?平面 EFGH, ...………………………………2分
平面 EFGH∩平面 ACD=GH,
∴EF∥GH,∴AC∥GH. ...………………………………4分
∴
AH
HD
=
CG
GD
=3,∴AH:HD=3:1. ...………………………………6分
(2)证明:∵EF∥GH,且EF
AC
=
1
3
,
GH
AC
=
1
4
,
∴EF≠GH,∴四边形 EFGH为梯形. ...………………………………8分
令 EH∩FG=P,则 P∈EH,而 EH?平面 ABD,
又 P∈FG,FG?平面 BCD, ...………………………………10分
平面 ABD∩平面 BCD=BD,
∴P∈BD,∴EH、FG、BD三线共点. .....……………………………12分
20.解:(1)∵
sin cos 2sin1
cos sin sin
A B C
A B B
? ? ? , .....……………………………1分
∴
cos sin sin cos 2sin
cos sin sin
A B A B C
A B B
?
? ,∴
sin( ) 2sin
cos sin sin
A B C
A B B
?
? ,……………………………3分
∴
sin 2sin
cos
C C
A
? ,又∵ sin 0C ? ,∴
1cos
2
A ? ,故
π
3
A ? .…………………………5分
(2)∵ ? ? 2 π π2sin 3cos2 1 2sin 2
4 3
f x x x x? ? ? ?? ? ? ? ? ?? ? ? ?
? ? ? ?
,…………………………7分
∴当
π π2
3 2
x ? ? ,即
5π
12
x ? 时, ? ?max 3f x ? ,此时
5π
12
B ? ,
π
4
C ? , 3a ? , ……9分
∵
sin sin
a c
A C
? ,∴
723sin 2 673sin
2
a cC
A
?
? ? ? , …………………………10分
则
1 1 6 2 9 3 3sin 3 6
2 2 4 4
S ac B ? ?? ? ? ? ? ? . …………………………12分
21.(1)∵AE⊥CD,∴AE⊥CE,AE⊥DE,
又CE DE E?? , AE? ?平面CDE. …………………………3分
由已知易得 AE∥BC,∴BC⊥平面 CDE; ………………………5分
2
(2)存在,当R点满足
1
4
AR AE? 时,面BDR ?面BDC.………………………6分
证明:如图,过点 E作 EF⊥CD交 CD于 F,易得
1
4
CF CD? ,…………………7分
由(1)可知 BC⊥平面 CDE ,则 BC⊥EF,∴EF⊥平面 BCD,…………………9分
过点 F作 FG∥BC交 BD于 G,连结 GR,则
3
4
FG BC? ,
又
1
4
AR AE? ,且 BC∥AE,∴四边形 EFGR是平行四边形, ………………11分
∴EF∥GR,∴GR⊥平面 BCD,又GR ?平面 BDR,面 BDR ?面BDC.…………12分
22.解:(1)当直线 l的斜率不存在时,直线 l的方程为 1x ? ? ,
此时与圆相切,符合题意; ………………………………1分
当直线 l的斜率存在时,设直线 l的方程为 ( 1)y k x? ? ,即 0kx y k? ? ? ,
若直线与圆相切,则圆心 (0,3) 到直线的距离等于半径 1,
所以
2
3
1
1
k
k
? ?
?
?
,解得
4
3
k ? ,
所以直线 l的方程为
4 ( 1)
3
y x? ? ,即 4 3 4 0x y? ? ? . ………………………………4分
综上,直线 l的方程为 1x ? ? 或 4 3 4 0x y? ? ? .
直线 l的方程为 1x ? ? 或 4 3 4 0x y? ? ? . ………………………………5分
(2)∵CM⊥MN,∴ ( ) = + =AM AN AC CM AC AN CM AC AN AN NA? ? ? ? ? ? ?
????? ???? ???? ????? ???? ???? ??? ????? ?? ??? ?? ? ? ????
若直线 l与 x轴垂直时,不符合题意; ………………………………7分
所以 l的斜率存在,设直线 l的方程为 ( 1)y k x? ? ,
则由
3 6
( 1) 1 3
3 6 0 5
1 3
kxy k x k
x y ky
k
? ?? ??? ?? ? ??? ?? ? ? ?? ? ?
? ??
,即
3 6 5( , )
1 3 1 3
k kN
k k
? ? ?
? ?
. ………………………9分
∴
5 5( , )
1 3 1 3
kAN
k k
? ?
?
? ?
????
,从而
5 15 5
1 3
=
1 3
=AN AN kAM AC
k k
? ?
? ? ? ? ?
? ?
???? ????? ?? ? ?????
.
综上所述, = 5AAM N ??
??? ??????
. ………………………12分
同课章节目录
