A典学案 第一章 第6课时 三角函数的应用 习题课件
文档属性
| 名称 | A典学案 第一章 第6课时 三角函数的应用 习题课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 00:00:00 | ||
图片预览


文档简介
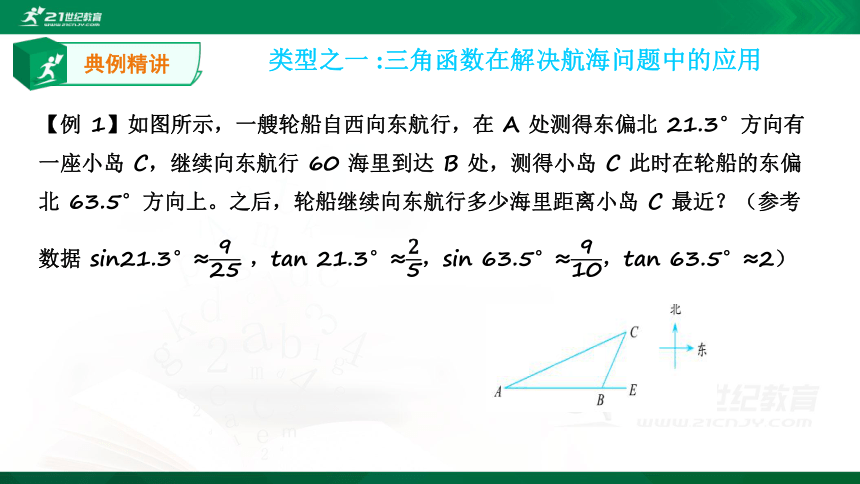
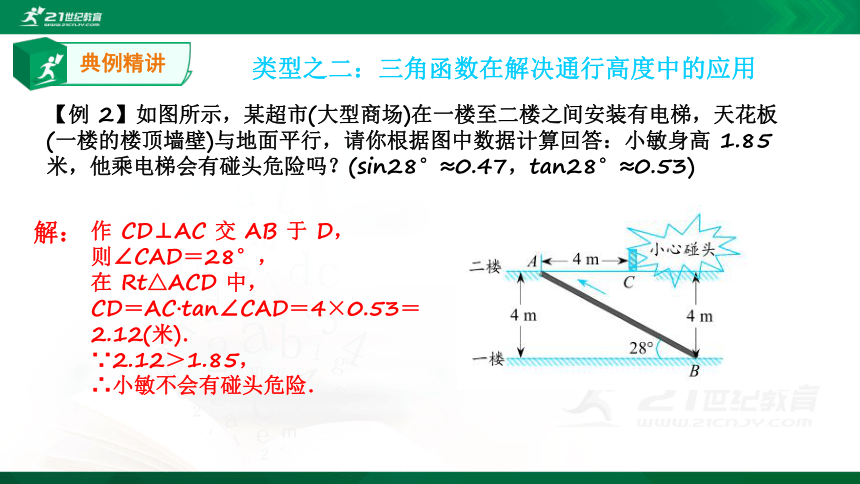
课件9张PPT。第一章 直角三角形的边角关系 第6课时 三角函数的应用北师大版 九年级下册类型之一 :三角函数在解决航海问题中的应用典例精讲?解: ?类型之二:三角函数在解决通行高度中的应用典例精讲【例 2】如图所示,某超市(大型商场)在一楼至二楼之间安装有电梯,天花板(一楼的楼顶墙壁)与地面平行,请你根据图中数据计算回答:小敏身高 1.85 米,他乘电梯会有碰头危险吗?(sin28°≈0.47,tan28°≈0.53)作 CD⊥AC 交 AB 于 D,
则∠CAD=28°,
在 Rt△ACD 中,
CD=AC·tan∠CAD=4×0.53=2.12(米).
∵2.12>1.85,
∴小敏不会有碰头危险.解: 课堂操练1.如图所示,为测量一幢大楼的高度,在地面上距离楼底 O 点 20 m 的点 A 处,测得楼顶 B 点的仰角为 65°,则这幢大楼的高度为( )(结果保留 3 个有效数字)
A.42.8 m B.42.80 m
C.42.9 m D.42.90 mC2.如图所示,从热气球 C 上测得建筑物 A,B 底部的俯角分别为 30°和 60°,若气球的高度 CD 为 150 米,且点 A,D,B 在同一直线上,则建筑物 A,B 间的距离为( )?C课堂操练3.如图所示,一艘船向正北航行,在 A 处看到灯塔 S在船的北偏东 30°的方向上,航行 12 海里到达 B 点,在 B 处看到灯塔 S 在船的北偏东 60°的方向上,此船继续沿正北方向航行过程中距灯塔 S 的最近距离是______海里。(不作近似计算)?4.如图所示,一艘船由 A 港沿北偏东 60°方向航行 20 km 至 B 港,然后再沿北偏西30方向航行20km至 C港.
(1)求 A,C 两港之间的距离(结果保留根号);
(2)确定 C 港在A港什么方向(求出方位角)?解: ?课堂操练谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
则∠CAD=28°,
在 Rt△ACD 中,
CD=AC·tan∠CAD=4×0.53=2.12(米).
∵2.12>1.85,
∴小敏不会有碰头危险.解: 课堂操练1.如图所示,为测量一幢大楼的高度,在地面上距离楼底 O 点 20 m 的点 A 处,测得楼顶 B 点的仰角为 65°,则这幢大楼的高度为( )(结果保留 3 个有效数字)
A.42.8 m B.42.80 m
C.42.9 m D.42.90 mC2.如图所示,从热气球 C 上测得建筑物 A,B 底部的俯角分别为 30°和 60°,若气球的高度 CD 为 150 米,且点 A,D,B 在同一直线上,则建筑物 A,B 间的距离为( )?C课堂操练3.如图所示,一艘船向正北航行,在 A 处看到灯塔 S在船的北偏东 30°的方向上,航行 12 海里到达 B 点,在 B 处看到灯塔 S 在船的北偏东 60°的方向上,此船继续沿正北方向航行过程中距灯塔 S 的最近距离是______海里。(不作近似计算)?4.如图所示,一艘船由 A 港沿北偏东 60°方向航行 20 km 至 B 港,然后再沿北偏西30方向航行20km至 C港.
(1)求 A,C 两港之间的距离(结果保留根号);
(2)确定 C 港在A港什么方向(求出方位角)?解: ?课堂操练谢谢21世纪教育网(www.21cnjy.com) 中小学教育资源网站 有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
