五年级上册数学课件数学好玩3 尝试与猜测 北师大版(共23张PPT)
文档属性
| 名称 | 五年级上册数学课件数学好玩3 尝试与猜测 北师大版(共23张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 3.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 14:02:39 | ||
图片预览







文档简介
(共25张PPT)
——鸡兔同笼
鸡兔同笼,有9个头,鸡、兔各有几只?
9
1
8
9
7
2
9
3
6
9
5
4
9
4
5
9
6
3
…
…
…
头/个 鸡/只 兔/只
我们和兔共有9个头
我们和鸡共有26条腿
鸡和兔各有多少只?
2条腿
4条腿
尝试题
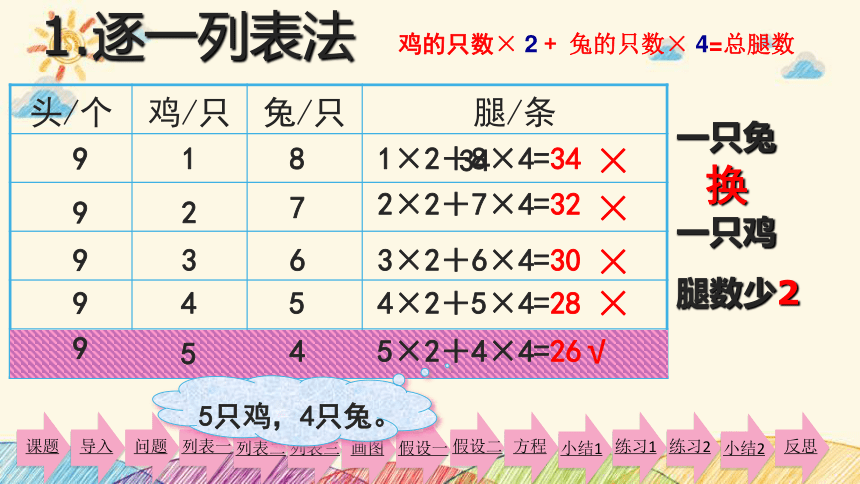
1.逐一列表法
9
1
8
1×2+8×4=34
9
7
2
2×2+7×4=32
9
3
6
3×2+6×4=30
9
5
4
5×2+4×4=26
鸡的只数× 2 + 兔的只数× 4=总腿数
9
4
5
4×2+5×4=28
34
腿数少2
√
×
×
×
×
头/个 鸡/只 兔/只 腿/条
绿色圃中小学教育网http://www.lspjy.com
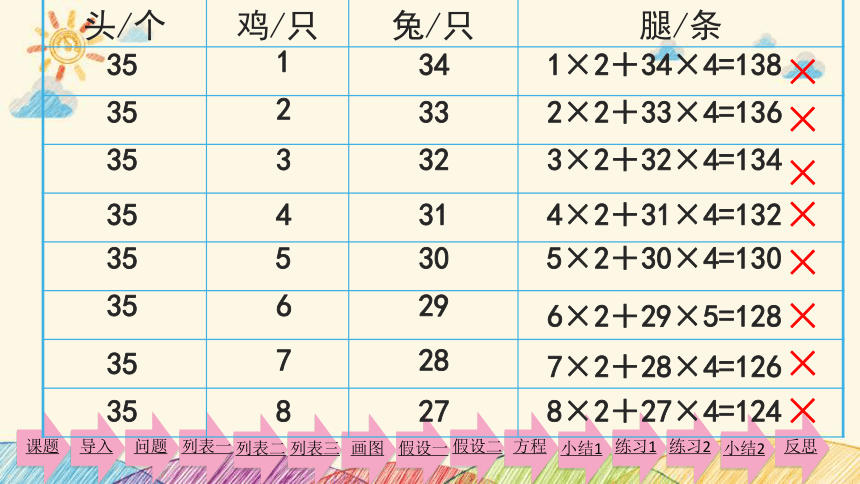
鸡兔同笼,有35个头,94条腿。鸡、兔各有几只?
35
1
34
1×2+34×4=138
35
33
2
2×2+33×4=136
35
3
32
3×2+32×4=134
35
4
31
4×2+31×4=132
35
5
30
5×2+30×4=130
35
6
29
6×2+29×5=128
35
7
28
7×2+28×4=126
35
8
27
8×2+27×4=124
×
×
×
×
×
×
×
×
头/个 鸡/只 兔/只 腿/条
35
1
34
1×2+34×4=138
35
25
10
10×2+25×4=120
35
20
15
20×2+15×4=100
35
25
10
25×2+10×4=90
35
24
11
24×2+11×4=92
35
23
12
23×2+12×5=94
2、跳跃列表法
×
×
×
×
×
√
头/个 鸡/只 兔/只 腿/条
3、取中列举法
35
17
18
17×2+18×4=106
35
20
15
20×2+15×4=100
35
12
23
23×2+12×4=94
35
22
13
22×2+13×4=96
×
×
×
√
头/个 鸡/只 兔/只 腿/条
4、画图法
4、画图法
(1) 先画35个圆圈表示35个头。
(2)再为每只动物画两条腿,
(3)把剩下的24条腿用完,要给其中的12只动物各添2条腿
35只动物就用完70条腿,
还多出24条腿。
这12只就是兔子,另外的23只就是鸡。
2×35=70(条)
94-70=24(条)
24÷(4-2)=12(只)
35-12=23(只)
5、假设算术法(一)
①假设35只全是鸡 , 共有多少条腿?
2×35=70(条)
②比实际少多少条腿?
94-70=24(条)
③每只兔比每只鸡多几条腿 ?
4-2=2(条)
④兔有多少只?
24÷2=12(只)
⑤鸡有多少只?
35-12=23(只)
答:鸡有23只,兔有12只。
5、假设算术法(二)
①假设35只全是兔算 ,那么共有多少条腿?
4×35=140(条)
②比实际多多少条腿?
140-94=46(条)
③每只兔比每只鸡多几条腿 ?
4-2=2(条)
④鸡有多少只?
46÷2=23(只)
⑤兔有多少只?
35-23=12(只)
答:鸡有23只,兔有12只。
解:设兔有x只,那么鸡有(35-x)只。
4x+2×(35-x)=94
4x+70-2x=94
2x=24
x=12
鸡: 35-12=23(只)
答:鸡有23只,兔有12只。
6、方程法
提示:
本题也可设鸡有x只,兔有(35一x)只
只列方程是2 x﹢ 4 (35 ﹣ x) =94 ,
式中涉及负数运算,
暂不适合我们现在学习,
为减轻不必要的负担,
可将每只动物腿多的只数设为x即可。
01
逐一列表法:
02
03
跳跃列表法:
取中列表法:
不重复,不遗漏;麻烦
简便,快捷
简便,快捷
绿色圃中小学教育网http://www.lspjy.com
龟鹤问题
1.停车场有三轮车和自行车共22辆,有59个轮子。自行车、三轮车各有几辆?
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元。1角和5角的硬币各有多少枚?
生活中的“鸡兔同笼”
1.停车场有三轮车和自行车共22辆,有59个轮子。自行车、三轮车各有几辆?
11
11
55
15
7
59
总数/辆 三轮车/辆 自行车/辆 总轮子数/个
22
22
22
22
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元。1角和5角的硬币各有多少枚?
13
14
8.3
17
10
6.7
20
7
5.5
21
6
5.1
总数/枚 1角/枚 5角/枚 总价值/元
27
27
27
27
猜测
验证
调整
数学模型
——鸡兔同笼
鸡兔同笼,有9个头,鸡、兔各有几只?
9
1
8
9
7
2
9
3
6
9
5
4
9
4
5
9
6
3
…
…
…
头/个 鸡/只 兔/只
我们和兔共有9个头
我们和鸡共有26条腿
鸡和兔各有多少只?
2条腿
4条腿
尝试题
1.逐一列表法
9
1
8
1×2+8×4=34
9
7
2
2×2+7×4=32
9
3
6
3×2+6×4=30
9
5
4
5×2+4×4=26
鸡的只数× 2 + 兔的只数× 4=总腿数
9
4
5
4×2+5×4=28
34
腿数少2
√
×
×
×
×
头/个 鸡/只 兔/只 腿/条
绿色圃中小学教育网http://www.lspjy.com
鸡兔同笼,有35个头,94条腿。鸡、兔各有几只?
35
1
34
1×2+34×4=138
35
33
2
2×2+33×4=136
35
3
32
3×2+32×4=134
35
4
31
4×2+31×4=132
35
5
30
5×2+30×4=130
35
6
29
6×2+29×5=128
35
7
28
7×2+28×4=126
35
8
27
8×2+27×4=124
×
×
×
×
×
×
×
×
头/个 鸡/只 兔/只 腿/条
35
1
34
1×2+34×4=138
35
25
10
10×2+25×4=120
35
20
15
20×2+15×4=100
35
25
10
25×2+10×4=90
35
24
11
24×2+11×4=92
35
23
12
23×2+12×5=94
2、跳跃列表法
×
×
×
×
×
√
头/个 鸡/只 兔/只 腿/条
3、取中列举法
35
17
18
17×2+18×4=106
35
20
15
20×2+15×4=100
35
12
23
23×2+12×4=94
35
22
13
22×2+13×4=96
×
×
×
√
头/个 鸡/只 兔/只 腿/条
4、画图法
4、画图法
(1) 先画35个圆圈表示35个头。
(2)再为每只动物画两条腿,
(3)把剩下的24条腿用完,要给其中的12只动物各添2条腿
35只动物就用完70条腿,
还多出24条腿。
这12只就是兔子,另外的23只就是鸡。
2×35=70(条)
94-70=24(条)
24÷(4-2)=12(只)
35-12=23(只)
5、假设算术法(一)
①假设35只全是鸡 , 共有多少条腿?
2×35=70(条)
②比实际少多少条腿?
94-70=24(条)
③每只兔比每只鸡多几条腿 ?
4-2=2(条)
④兔有多少只?
24÷2=12(只)
⑤鸡有多少只?
35-12=23(只)
答:鸡有23只,兔有12只。
5、假设算术法(二)
①假设35只全是兔算 ,那么共有多少条腿?
4×35=140(条)
②比实际多多少条腿?
140-94=46(条)
③每只兔比每只鸡多几条腿 ?
4-2=2(条)
④鸡有多少只?
46÷2=23(只)
⑤兔有多少只?
35-23=12(只)
答:鸡有23只,兔有12只。
解:设兔有x只,那么鸡有(35-x)只。
4x+2×(35-x)=94
4x+70-2x=94
2x=24
x=12
鸡: 35-12=23(只)
答:鸡有23只,兔有12只。
6、方程法
提示:
本题也可设鸡有x只,兔有(35一x)只
只列方程是2 x﹢ 4 (35 ﹣ x) =94 ,
式中涉及负数运算,
暂不适合我们现在学习,
为减轻不必要的负担,
可将每只动物腿多的只数设为x即可。
01
逐一列表法:
02
03
跳跃列表法:
取中列表法:
不重复,不遗漏;麻烦
简便,快捷
简便,快捷
绿色圃中小学教育网http://www.lspjy.com
龟鹤问题
1.停车场有三轮车和自行车共22辆,有59个轮子。自行车、三轮车各有几辆?
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元。1角和5角的硬币各有多少枚?
生活中的“鸡兔同笼”
1.停车场有三轮车和自行车共22辆,有59个轮子。自行车、三轮车各有几辆?
11
11
55
15
7
59
总数/辆 三轮车/辆 自行车/辆 总轮子数/个
22
22
22
22
2.乐乐的储蓄罐里有1角和5角的硬币共27枚,总值5.1元。1角和5角的硬币各有多少枚?
13
14
8.3
17
10
6.7
20
7
5.5
21
6
5.1
总数/枚 1角/枚 5角/枚 总价值/元
27
27
27
27
猜测
验证
调整
数学模型
同课章节目录
- 一 小数除法
- 1 精打细算
- 2 打扫卫生
- 3 谁打电话的时间长
- 4 人民币兑换
- 5 除得尽吗
- 6 调查“生活垃圾”
- 二 轴对称和平移
- 1 轴对称再认识(一)
- 2 轴对称再认识(二)
- 3 平移
- 4 欣赏与设计
- 三 倍数与因数
- 1 倍数与因数
- 2 探索活动:2、5的倍数的特征
- 3 探索活动:3的倍数的特征
- 4 找因数
- 5 找质数
- 四 多边形的面积
- 1 比较图形的面积
- 2 认识底和高
- 3 探索活动:平行四边形的面积
- 4 探索活动:三角形的面积
- 5 探索活动:梯形的面积
- 五 分数的意义
- 1 分数的再认识(一)
- 2 分数的再认识(二)
- 3 分饼
- 4 分数与除法
- 5 分数基本性质
- 6 找最大的公因数
- 7 约分
- 8 找最小的公倍数
- 9 分数的大小
- 六 组合图形的面积
- 1 组合图形的面积
- 2 探索活动:成长的脚印
- 3 公顷、平方千米
- 数学好玩
- 1 设计秋游方案
- 2 图形中的规律
- 3 尝试与猜测
- 七 可能性
- 1 谁先走
- 2 摸球游戏
