五年级上册数学试 题-7.土地的面积 冀教版(2014秋)(含解析)
文档属性
| 名称 | 五年级上册数学试 题-7.土地的面积 冀教版(2014秋)(含解析) | 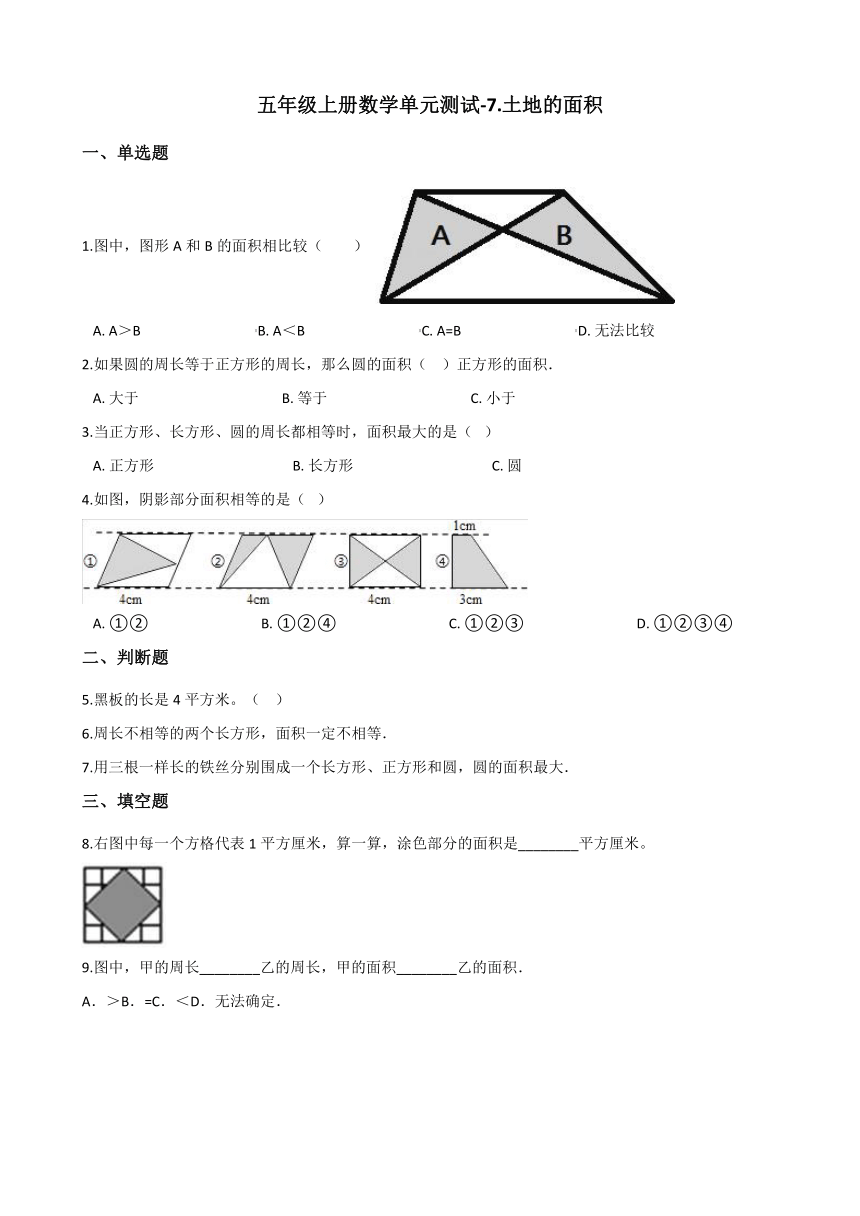 | |
| 格式 | zip | ||
| 文件大小 | 71.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-24 20:20:00 | ||
图片预览



文档简介
五年级上册数学单元测试-7.土地的面积
一、单选题
1.图中,图形A和B的面积相比较( )
A.?A>B?????????????????????????????????B.?A<B?????????????????????????????????C.?A=B?????????????????????????????????D.?无法比较
2.如果圆的周长等于正方形的周长,那么圆的面积(?? )正方形的面积.
A.?大于?????????????????????????????????????????B.?等于?????????????????????????????????????????C.?小于
3.当正方形、长方形、圆的周长都相等时,面积最大的是(? )
A.?正方形????????????????????????????????????????B.?长方形????????????????????????????????????????C.?圆
4.如图,阴影部分面积相等的是(? )
A.?①②????????????????????????????????B.?①②④????????????????????????????????C.?①②③????????????????????????????????D.?①②③④
二、判断题
5.黑板的长是4平方米。(?? )
6.周长不相等的两个长方形,面积一定不相等.
7.用三根一样长的铁丝分别围成一个长方形、正方形和圆,圆的面积最大.
三、填空题
8.右图中每一个方格代表1平方厘米,算一算,涂色部分的面积是________平方厘米。
9.图中,甲的周长________乙的周长,甲的面积________乙的面积.
A.>B.=C.<D.无法确定.
10.如图若以长方形的一条宽为轴旋转一周后,甲乙两部分所成的立体图形的体积比是________.
四、解答题
11.仔细观察,这两个图形的面积一样大吗?为什么?
五、综合题
12.王大伯沿着围墙围了一块长5米,宽3米的空地养鸡。
(1)这块空地的面积是多少平方米?
(2)如果给这个空地围上篱笆,篱笆有多长?
六、应用题
13.小红每天坚持锻炼身体,她绕着小区里的正方形荷花池跑步,跑一圈正好是240米,这个正方形荷花池的面积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,
这两个新三角形是等底等高,面积相等,空白部分是公共部分,所以两个阴影三角形的面积相等.
故选:C.
【分析】由图可知,两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,由于这两个新三角形是等底等高的,面积相等,所以两个阴影三角形的面积是相等的.
2.【答案】 A
【解析】【解答】解:设圆及正方形的周长为a,
由圆周长公式C=2πr得,圆的半径r= ,
所以圆的面积为:S圆=πr2=π( )2= ;
因为正方形的周长为a,所以边长为 ,面积为:S正方形=( )2= ,
又因为4π<4×4,即4π<16,
所以 > ,
即S圆>S正方形,
故选:A.
【分析】可设圆及正方形的周长为a,则由圆周长公式C=2πr,可求得圆的半径r= ,从而圆的面积可表示为π( )2;另外,正方形的周长为a,则边长为 ,所以面积为( )2 , 再比较出π( )2和( )2的大小即可得出答案.
3.【答案】 C
【解析】【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的面积为: ≈20.38;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的正方形、长方形和圆形,圆面积最大.
故选:C.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.此题主要考查长方形、正方形、圆形的面积公式及灵活运用,解答此题可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
4.【答案】 D
【解析】【解答】解:前三图中,阴影部分均为平行四边形(长方形)面积的一半,而三个平行四边形(长方形)的面积相等;
梯形的上底加下底也是4厘米,也等于平行四边形面积的一半;
由此可得:阴影部分的面积都相等.
故选:D.
【分析】在平行四边形①②中和长方形③中,阴影部分面积都是平行四边形或者长方形面积的一半,梯形的上底加下底也是4厘米,也等于平行四边形面积的一半,由此即可判断它们面积的大小.此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.
二、判断题
5.【答案】 错误
【解析】【解答】长度的单位是米,正确的说法是:黑板的长度是4米
【分析】考察对常见的单位的认识和理解
6.【答案】错误
【解析】【解答】解:可以举例证明,当长方形的周长是24厘米和18厘米时:
一种长是10厘米,宽是2厘米,面积是20平方厘米;
另一种长是5厘米,宽是4厘米,面积是20平方厘米;
很显然20平方厘米等于20平方厘米,但是它们的周长却不相等;
所以周长不相等的两个长方形,面积一定不相等,这种说法是错误的.
故答案为:错误.
【分析】如果两个长方形的周长不相等,长与宽相差越小面积就越大,当长和宽相等时(正方形)面积最大.由此解答.此题考查的目的是,当两个长方形的周长不相等,这样的长方形有多种情况,长与宽的差越小面积就越大.
7.【答案】 正确
【解析】【解答】解:正方形的面积:
16÷4=4(厘米),
4×4=16(平方厘米);
长方形的面积:
16÷2=8(厘米),
8=5+3,
5×3=15(平方厘米);
圆的面积:
16÷3.14÷2
=2.5477,
≈2.5(厘米);
3.14×2.52 ,
=3.14×6.25,
=19.625(平方厘米);
圆的面积>正方形的面积>长方形的面积,
故题干中的说法是正确的.
故答案为:正确.
【分析】我们假设三根一样长的铁丝都是16厘米,分别求出长方形,正方形,圆的面积,再作出判断.则长方形的长是5厘米,宽3厘米,正方形的边长4厘米,求出圆的半径进一步求出面积.本题考查了正方形,长方形,圆的面积公式的运用,考查了学生灵活解决问题的能力.
三、填空题
8.【答案】 8
【解析】【解答】从图中看,大的正方形被分割成好几块,不难看出两个小的三角形拼在一起就是一个新的小正方形,由四个小格构成,一共能拼得两个小正方形,面积是8平方厘米,而原来大的正方形有16个小格,面积是16平方厘米,所以涂色部分的面积是8平方厘米
【分析】通过读图来考察对图形面积的认识
9.【答案】 B;A
【解析】【解答】解:从图上看出:甲的周长是正方形的两边长加上弧线的长,
乙的周长也是正方形的两边长加上弧线的长,
所以甲的周长=乙的周长,
如图:连接对角线,
从图上看出甲的面积是三角形面积加上a部分的面积=边长×边长+a,
乙的面积是三角形面积减去a部分的面积=边长×边长﹣a,
所以甲的面积>乙的面积.
故答案为:B,A.
【分析】图形的周长是指围绕图形一周的长度.甲的周长是正方形的两边长加上弧线的长,乙的周长也是正方形的两边长加上弧线的长,先连接对角线如图,从图上看出甲的面积是三角形面积加上a部分的面积,乙的面积是三角形面积减去a部分的面积,由此可比大小.此题是对图形的周长及面积的理解与运用.
10.【答案】1:2
【解析】【解答】解:以长方形的一条宽为轴旋转一周后,得到的立体图形是圆柱,甲旋转后是一个与圆柱等底等高的圆锥,甲的体积是这个圆柱体积的 ,
那么乙所形成的立体图形的体积占这个圆柱体积的1﹣ = ,
即甲乙两部分所成的立体图形的体积比是: : = =1:2;
故答案为:1:2.
【分析】根据题意,以长方形的一条宽为轴旋转一周后,得到的立体图形是圆柱,圆柱的高等于长方形的宽,底面半径等于长方形的长;甲旋转后是一个与圆柱等底等高的圆锥,等底等高的圆锥的体积是圆柱体积的 ,那么乙所形成的立体图形的体积占这个圆柱体积的1﹣ = ,因此解答.此题主要根据等底等高的圆锥的体积是圆柱体积的 ,此题可以理解为把一个圆柱削成一个最大的圆锥,这个圆锥的体积与削去部分的体积的比是1:2.由此解决问题.
四、解答题
11.【答案】一样大;因为他们都占10个小方格。
【解析】【解答】一样大;因为他们都占10个小方格。
【分析】用面积的定义,以及用数方格的方法可以分别算出着个图形的面积。再次进行比较大小。
五、综合题
12.【答案】 (1)解:空地的面积=5×3=15(平方米)
答:空地的面积是15平方米
(2)解:需要的篱笆:5+3+3=11(米)
答:空地的面积是15平方米,篱笆的长度是11米
【解析】【解答】(1)空地的面积=5×3=15(平方米)(2)需要的篱笆:5+3+3=11(米)
答:空地的面积是15平方米,篱笆的长度是11米
【分析】本题需要注意的是篱笆一面是靠墙的所以计算的时候要减去长方形长的长度
六、应用题
13.【答案】 解:正方形的四条边都相等,所以一条边长为240÷4=60(米)
荷花池的面积=60×60=3600(平方米)
答:这个正方形的荷花池面积是3600平方米
【解析】【分析】考察正方形面积的计算
一、单选题
1.图中,图形A和B的面积相比较( )
A.?A>B?????????????????????????????????B.?A<B?????????????????????????????????C.?A=B?????????????????????????????????D.?无法比较
2.如果圆的周长等于正方形的周长,那么圆的面积(?? )正方形的面积.
A.?大于?????????????????????????????????????????B.?等于?????????????????????????????????????????C.?小于
3.当正方形、长方形、圆的周长都相等时,面积最大的是(? )
A.?正方形????????????????????????????????????????B.?长方形????????????????????????????????????????C.?圆
4.如图,阴影部分面积相等的是(? )
A.?①②????????????????????????????????B.?①②④????????????????????????????????C.?①②③????????????????????????????????D.?①②③④
二、判断题
5.黑板的长是4平方米。(?? )
6.周长不相等的两个长方形,面积一定不相等.
7.用三根一样长的铁丝分别围成一个长方形、正方形和圆,圆的面积最大.
三、填空题
8.右图中每一个方格代表1平方厘米,算一算,涂色部分的面积是________平方厘米。
9.图中,甲的周长________乙的周长,甲的面积________乙的面积.
A.>B.=C.<D.无法确定.
10.如图若以长方形的一条宽为轴旋转一周后,甲乙两部分所成的立体图形的体积比是________.
四、解答题
11.仔细观察,这两个图形的面积一样大吗?为什么?
五、综合题
12.王大伯沿着围墙围了一块长5米,宽3米的空地养鸡。
(1)这块空地的面积是多少平方米?
(2)如果给这个空地围上篱笆,篱笆有多长?
六、应用题
13.小红每天坚持锻炼身体,她绕着小区里的正方形荷花池跑步,跑一圈正好是240米,这个正方形荷花池的面积是多少?
参考答案
一、单选题
1.【答案】 C
【解析】【解答】解:两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,
这两个新三角形是等底等高,面积相等,空白部分是公共部分,所以两个阴影三角形的面积相等.
故选:C.
【分析】由图可知,两个阴影三角形分别加上顶部的空白三角形后组成两个新的三角形,由于这两个新三角形是等底等高的,面积相等,所以两个阴影三角形的面积是相等的.
2.【答案】 A
【解析】【解答】解:设圆及正方形的周长为a,
由圆周长公式C=2πr得,圆的半径r= ,
所以圆的面积为:S圆=πr2=π( )2= ;
因为正方形的周长为a,所以边长为 ,面积为:S正方形=( )2= ,
又因为4π<4×4,即4π<16,
所以 > ,
即S圆>S正方形,
故选:A.
【分析】可设圆及正方形的周长为a,则由圆周长公式C=2πr,可求得圆的半径r= ,从而圆的面积可表示为π( )2;另外,正方形的周长为a,则边长为 ,所以面积为( )2 , 再比较出π( )2和( )2的大小即可得出答案.
3.【答案】 C
【解析】【解答】解:为了便于理解,假设正方形、长方形和圆形的周长都是16,
则圆的面积为: ≈20.38;
正方形的边长为:16÷4=4,面积为:4×4=16;
长方形长宽越接近面积越大,就取长为5宽为3,面积为:5×3=15,
当长方形的长和宽最接近时面积也小于16;
所以周长相等的正方形、长方形和圆形,圆面积最大.
故选:C.
【分析】周长相等的正方形、长方形和圆形,谁的面积最大,谁面积最小,可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.此题主要考查长方形、正方形、圆形的面积公式及灵活运用,解答此题可以先假设这三种图形的周长是多少,再利用这三种图形的面积公式,分别计算出它们的面积,最后比较这三种图形面积的大小.
4.【答案】 D
【解析】【解答】解:前三图中,阴影部分均为平行四边形(长方形)面积的一半,而三个平行四边形(长方形)的面积相等;
梯形的上底加下底也是4厘米,也等于平行四边形面积的一半;
由此可得:阴影部分的面积都相等.
故选:D.
【分析】在平行四边形①②中和长方形③中,阴影部分面积都是平行四边形或者长方形面积的一半,梯形的上底加下底也是4厘米,也等于平行四边形面积的一半,由此即可判断它们面积的大小.此题主要考查等底等高的三角形面积相等及平行四边形的特点.据图即可以作出判断.
二、判断题
5.【答案】 错误
【解析】【解答】长度的单位是米,正确的说法是:黑板的长度是4米
【分析】考察对常见的单位的认识和理解
6.【答案】错误
【解析】【解答】解:可以举例证明,当长方形的周长是24厘米和18厘米时:
一种长是10厘米,宽是2厘米,面积是20平方厘米;
另一种长是5厘米,宽是4厘米,面积是20平方厘米;
很显然20平方厘米等于20平方厘米,但是它们的周长却不相等;
所以周长不相等的两个长方形,面积一定不相等,这种说法是错误的.
故答案为:错误.
【分析】如果两个长方形的周长不相等,长与宽相差越小面积就越大,当长和宽相等时(正方形)面积最大.由此解答.此题考查的目的是,当两个长方形的周长不相等,这样的长方形有多种情况,长与宽的差越小面积就越大.
7.【答案】 正确
【解析】【解答】解:正方形的面积:
16÷4=4(厘米),
4×4=16(平方厘米);
长方形的面积:
16÷2=8(厘米),
8=5+3,
5×3=15(平方厘米);
圆的面积:
16÷3.14÷2
=2.5477,
≈2.5(厘米);
3.14×2.52 ,
=3.14×6.25,
=19.625(平方厘米);
圆的面积>正方形的面积>长方形的面积,
故题干中的说法是正确的.
故答案为:正确.
【分析】我们假设三根一样长的铁丝都是16厘米,分别求出长方形,正方形,圆的面积,再作出判断.则长方形的长是5厘米,宽3厘米,正方形的边长4厘米,求出圆的半径进一步求出面积.本题考查了正方形,长方形,圆的面积公式的运用,考查了学生灵活解决问题的能力.
三、填空题
8.【答案】 8
【解析】【解答】从图中看,大的正方形被分割成好几块,不难看出两个小的三角形拼在一起就是一个新的小正方形,由四个小格构成,一共能拼得两个小正方形,面积是8平方厘米,而原来大的正方形有16个小格,面积是16平方厘米,所以涂色部分的面积是8平方厘米
【分析】通过读图来考察对图形面积的认识
9.【答案】 B;A
【解析】【解答】解:从图上看出:甲的周长是正方形的两边长加上弧线的长,
乙的周长也是正方形的两边长加上弧线的长,
所以甲的周长=乙的周长,
如图:连接对角线,
从图上看出甲的面积是三角形面积加上a部分的面积=边长×边长+a,
乙的面积是三角形面积减去a部分的面积=边长×边长﹣a,
所以甲的面积>乙的面积.
故答案为:B,A.
【分析】图形的周长是指围绕图形一周的长度.甲的周长是正方形的两边长加上弧线的长,乙的周长也是正方形的两边长加上弧线的长,先连接对角线如图,从图上看出甲的面积是三角形面积加上a部分的面积,乙的面积是三角形面积减去a部分的面积,由此可比大小.此题是对图形的周长及面积的理解与运用.
10.【答案】1:2
【解析】【解答】解:以长方形的一条宽为轴旋转一周后,得到的立体图形是圆柱,甲旋转后是一个与圆柱等底等高的圆锥,甲的体积是这个圆柱体积的 ,
那么乙所形成的立体图形的体积占这个圆柱体积的1﹣ = ,
即甲乙两部分所成的立体图形的体积比是: : = =1:2;
故答案为:1:2.
【分析】根据题意,以长方形的一条宽为轴旋转一周后,得到的立体图形是圆柱,圆柱的高等于长方形的宽,底面半径等于长方形的长;甲旋转后是一个与圆柱等底等高的圆锥,等底等高的圆锥的体积是圆柱体积的 ,那么乙所形成的立体图形的体积占这个圆柱体积的1﹣ = ,因此解答.此题主要根据等底等高的圆锥的体积是圆柱体积的 ,此题可以理解为把一个圆柱削成一个最大的圆锥,这个圆锥的体积与削去部分的体积的比是1:2.由此解决问题.
四、解答题
11.【答案】一样大;因为他们都占10个小方格。
【解析】【解答】一样大;因为他们都占10个小方格。
【分析】用面积的定义,以及用数方格的方法可以分别算出着个图形的面积。再次进行比较大小。
五、综合题
12.【答案】 (1)解:空地的面积=5×3=15(平方米)
答:空地的面积是15平方米
(2)解:需要的篱笆:5+3+3=11(米)
答:空地的面积是15平方米,篱笆的长度是11米
【解析】【解答】(1)空地的面积=5×3=15(平方米)(2)需要的篱笆:5+3+3=11(米)
答:空地的面积是15平方米,篱笆的长度是11米
【分析】本题需要注意的是篱笆一面是靠墙的所以计算的时候要减去长方形长的长度
六、应用题
13.【答案】 解:正方形的四条边都相等,所以一条边长为240÷4=60(米)
荷花池的面积=60×60=3600(平方米)
答:这个正方形的荷花池面积是3600平方米
【解析】【分析】考察正方形面积的计算
