人教版八年级数学上册第十三章 轴对称13.1轴对称:垂直平分线教学课件(2课时共20张)
文档属性
| 名称 | 人教版八年级数学上册第十三章 轴对称13.1轴对称:垂直平分线教学课件(2课时共20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 937.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 00:00:00 | ||
图片预览





文档简介
(共20张PPT)
垂直平分线的定义
学习目标
垂直平分线的性质
中垂线
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.
轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.
对称轴是任何一对对称点所连线段的垂直平分线.
性质定理:在线段垂直平分线上的点到线段两个端点距离都相等(纯粹性)。
逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上(完备性)。
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
辨析:
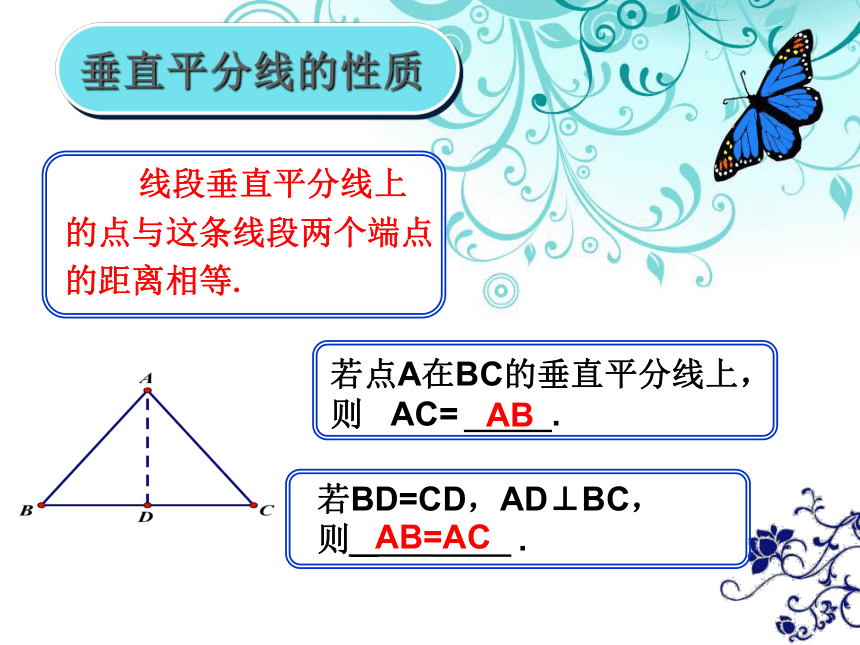
垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
AB
AB=AC
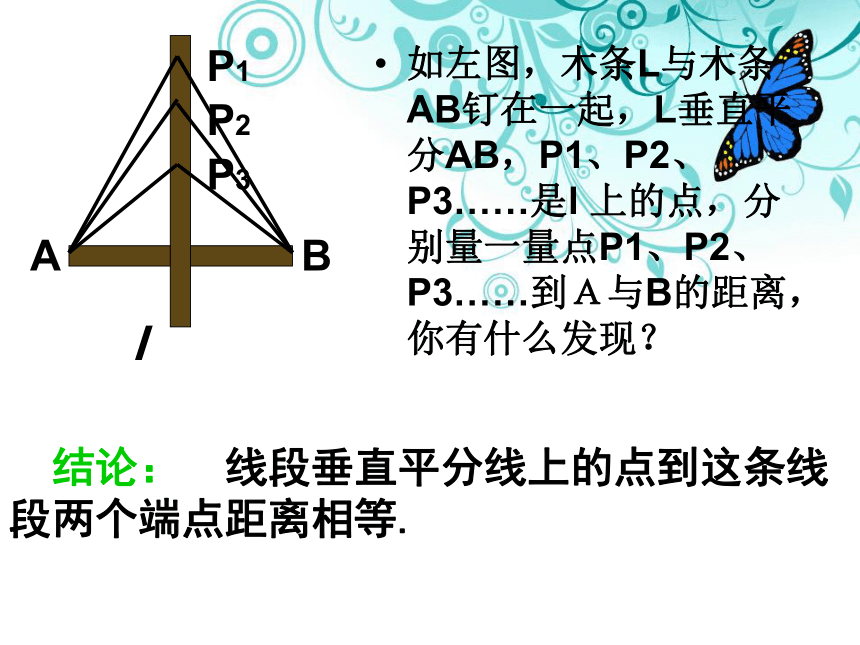
如左图,木条L与木条AB钉在一起,L垂直平分AB,P1、P2、P3……是l 上的点,分别量一量点P1、P2、P3……到A与B的距离,你有什么发现?
结论: 线段垂直平分线上的点到这条线段两个端点距离相等.
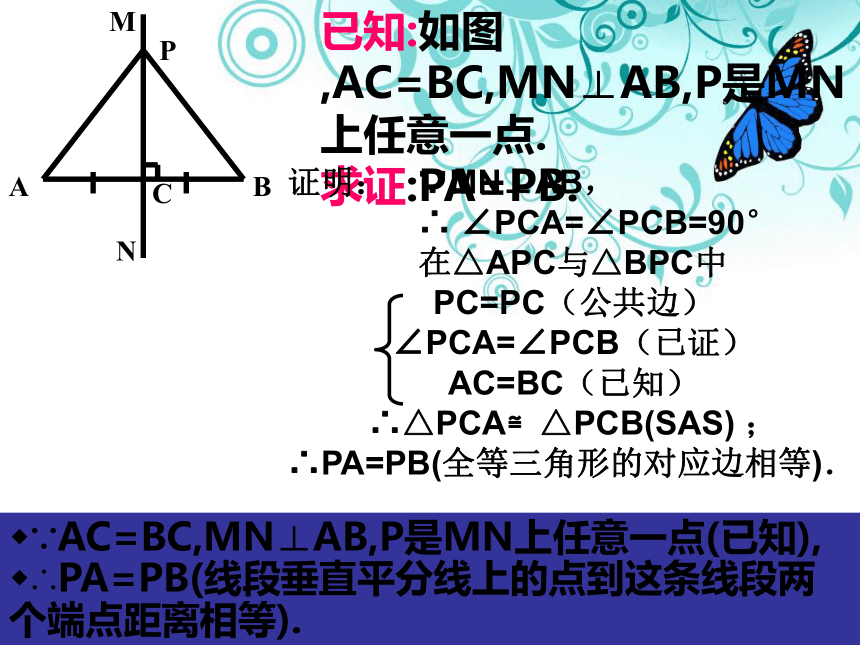
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
证明: ∵MN⊥AB,
∴ ∠PCA=∠PCB=90°
在△APC与△BPC中
PC=PC(公共边)
∠PCA=∠PCB(已证)
AC=BC(已知) ∴△PCA≌△PCB(SAS) ;
∴PA=PB(全等三角形的对应边相等).
这个结论是经常用来证明两条线段相等的根据之一.
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
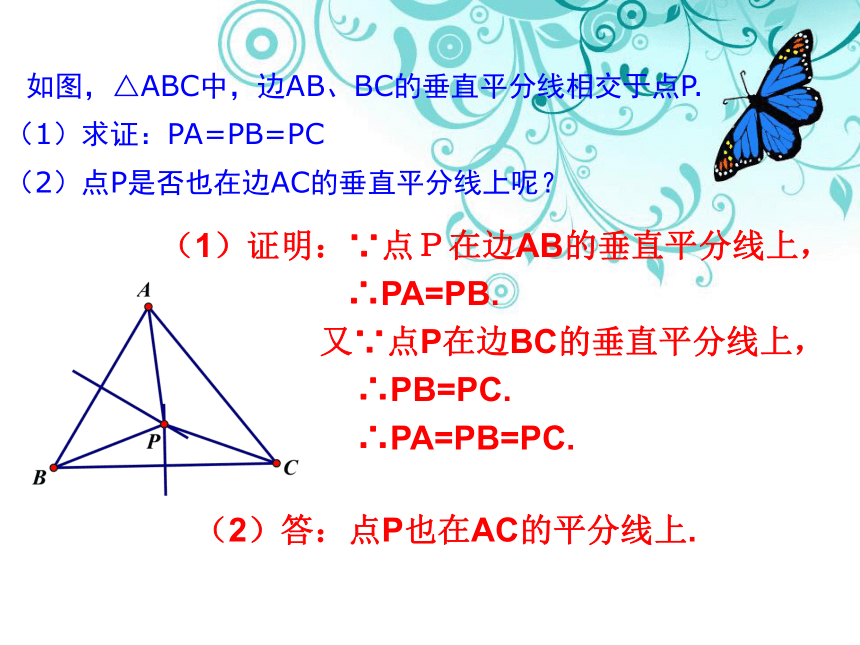
如图,△ABC中,边AB、BC的垂直平分线相交于点P.
(1)求证:PA=PB=PC
(2)点P是否也在边AC的垂直平分线上呢?
(1)证明:∵点P在边AB的垂直平分线上,
∴PA=PB.
又∵点P在边BC的垂直平分线上,
∴PB=PC.
∴PA=PB=PC.
(2)答:点P也在AC的平分线上.
如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.
即:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
如果把这个命题反过来说,还成立吗?
你能证明这个结论吗?
已知:线段AB,点P是平面内一点且PA=PB.
求证:P点在AB的
垂直平分线上.
证明:过点P作已知线段AB的垂线PC,∴∠PCA=∠PCB=90°
在Rt△PAC≌Rt△PBC中 PA=PB,
PC=PC(公共边),
∴Rt△PAC≌Rt△PBC(HL)
∴AC=BC(全等三角形对应角相等)
即,P点在AB的垂直平分线上
结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
BC的垂直平分线上
线段垂直平分线的判定:
定理:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
练习:如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
解:
∵ED是线段AB的垂直平分线
∴
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=
=
=
BD=AD
AD+DC+BC
AC+BC
12+7=19
本节课你有哪些收获?
一、线段垂直平分线的的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
二、逆定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
回忆与思考
1、什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2、线段垂直平分线有什么性质?
线段垂直平分线上的点与这条线段的两个端点的距离相等 。
你能画图说明吗?
基本作图:
作线段的垂直平分线。
已知:线段AB,
求作:线段AB的垂直平分线。
C
D
作法:
(2)作直线CD。
CD即为所求。
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴。
例题:
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
例题:
如图,在Rt△ABC中,∠C=90,DE是AB的垂直平分线,连接AE,∠CAE:∠DAE=1:2,求∠B的度数。
例题:
如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。
C
垂直平分线的定义
学习目标
垂直平分线的性质
中垂线
图形轴对称的性质
如果两个图形关于某条直线对称,那么对称轴是任何一对对称点所连线段的垂直平分线.
轴对称图形的对称轴是任何一对对称点所连线段的垂直平分线.
对称轴是任何一对对称点所连线段的垂直平分线.
性质定理:在线段垂直平分线上的点到线段两个端点距离都相等(纯粹性)。
逆定理:与线段两个端点距离相等的点都在线段的垂直平分线上(完备性)。
线段垂直平分线的集合定义:
线段垂直平分线可以看作是与线段两个端点距离相等的所有点的集合。
辨析:
垂直平分线的性质
线段垂直平分线上的点与这条线段两个端点的距离相等.
AB
AB=AC
如左图,木条L与木条AB钉在一起,L垂直平分AB,P1、P2、P3……是l 上的点,分别量一量点P1、P2、P3……到A与B的距离,你有什么发现?
结论: 线段垂直平分线上的点到这条线段两个端点距离相等.
已知:如图,AC=BC,MN⊥AB,P是MN上任意一点.
求证:PA=PB.
证明: ∵MN⊥AB,
∴ ∠PCA=∠PCB=90°
在△APC与△BPC中
PC=PC(公共边)
∠PCA=∠PCB(已证)
AC=BC(已知) ∴△PCA≌△PCB(SAS) ;
∴PA=PB(全等三角形的对应边相等).
这个结论是经常用来证明两条线段相等的根据之一.
∵AC=BC,MN⊥AB,P是MN上任意一点(已知),
∴PA=PB(线段垂直平分线上的点到这条线段两个端点距离相等).
如图,△ABC中,边AB、BC的垂直平分线相交于点P.
(1)求证:PA=PB=PC
(2)点P是否也在边AC的垂直平分线上呢?
(1)证明:∵点P在边AB的垂直平分线上,
∴PA=PB.
又∵点P在边BC的垂直平分线上,
∴PB=PC.
∴PA=PB=PC.
(2)答:点P也在AC的平分线上.
如果有一个点到线段两个端点的距离相等,那么这个点在这条线段的垂直平分线上.
即:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
如果把这个命题反过来说,还成立吗?
你能证明这个结论吗?
已知:线段AB,点P是平面内一点且PA=PB.
求证:P点在AB的
垂直平分线上.
证明:过点P作已知线段AB的垂线PC,∴∠PCA=∠PCB=90°
在Rt△PAC≌Rt△PBC中 PA=PB,
PC=PC(公共边),
∴Rt△PAC≌Rt△PBC(HL)
∴AC=BC(全等三角形对应角相等)
即,P点在AB的垂直平分线上
结论:与一条线段两个端点距离相等的点,在这条线段的垂直平分线上.
BC的垂直平分线上
线段垂直平分线的判定:
定理:到线段两个端点的距离相等的点在这条线段的垂直平分线上.
∵PA=PB(已知),
∴点P在AB的垂直平分线上(到一条线段两个端点距离相等的点,在这条线段的垂直平分线上).
练习:如图,若AC=12,BC=7,AB的垂直平分线交AB于E,交AC于D,求△BCD的周长。
解:
∵ED是线段AB的垂直平分线
∴
∵ △BCD的周长=BD+DC+BC
∴ △BCD的周长=
=
=
BD=AD
AD+DC+BC
AC+BC
12+7=19
本节课你有哪些收获?
一、线段垂直平分线的的性质定理:
线段垂直平分线上的点与这条线段两个端点的距离相等。
二、逆定理:
与一条线段两个端点距离相等的点,在这条线段的垂直平分线上。
回忆与思考
1、什么叫线段垂直平分线?
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫中垂线。
2、线段垂直平分线有什么性质?
线段垂直平分线上的点与这条线段的两个端点的距离相等 。
你能画图说明吗?
基本作图:
作线段的垂直平分线。
已知:线段AB,
求作:线段AB的垂直平分线。
C
D
作法:
(2)作直线CD。
CD即为所求。
结论:对于轴对称图形,只要找到任意一组对应点,作出对应点所连线段的垂直平分线,就得到此图形的对称轴。
例题:
有A、B、C三个村庄,现准备要建一所学校,要求学校到三个村庄的距离相等,请你确定学校的位置。
A
B
C
如图,△ABC中,边AB、BC的垂直平分线交于点P。
(1)求证:PA=PB=PC。
(2)点P是否也在边AC的垂直平分线上呢?由此你能得出什么结论?
结论:三角形三条边的垂直平分线相交于一点,这个点到三角形三个顶点的距离相等。
例题:
如图,在Rt△ABC中,∠C=90,DE是AB的垂直平分线,连接AE,∠CAE:∠DAE=1:2,求∠B的度数。
例题:
如下图△ABC中,AC=16cm,DE为AB的垂直平分线, △BCE的周长为26cm,求BC的长。
C
