4.4 探索三角形相似的条件 同步练习(解析版)
文档属性
| 名称 | 4.4 探索三角形相似的条件 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 16:48:12 | ||
图片预览



文档简介
初中数学北师大版九年级上学期 第四章 4.4 探索三角形相似的条件
一、单选题
1.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(?? )
A.?3对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?8对
2.下列命题中,是真命题的是(?? )
A.?两直线平行,内错角相等????????????????????????????????????B.?两个锐角的和是钝角 C.?直角三角形都相似??????????????????????????????????????????????D.?正六边形的内角和为360°21世纪教育网版权所有
3.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
4.如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是(?? )
A.?∠B=∠D???????????????????????B.?∠C=∠AED???????????????????????C.?= ???????????????????????D.?=
5.如图,下列条件中不能判定△ACD∽△ABC的是(??? )
A.?∠ADC=∠ACB???????????????????B.????????????????????C.?∠ACD=∠B???????????????????D.?AC2=AD?AB
6.如图,∠1=∠2,DE∥AC,则图中的相似三角形有(?? )
A.?2对???????????????????????????????????????B.?3对???????????????????????????????????????C.?4对???????????????????????????????????????D.?5对
7.“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置(?? )www-2-1-cnjy-com
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
二、填空题
8.如图,在△ABC和△ADE中, = ,要使△ABC 和 △ADE相似,还需要添加一个条件,这个条件是________ 2-1-c-n-j-y
9.如图,若使△ACD∽△ABC,需添加的一个条件是________.
三、综合题
10.已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A与点O重合,顶点C在∠MON内部 21*cnjy*com
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法); 【来源:21cnj*y.co*m】
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1 , 试猜想∠BCC1为多少度,并证明你的猜想.
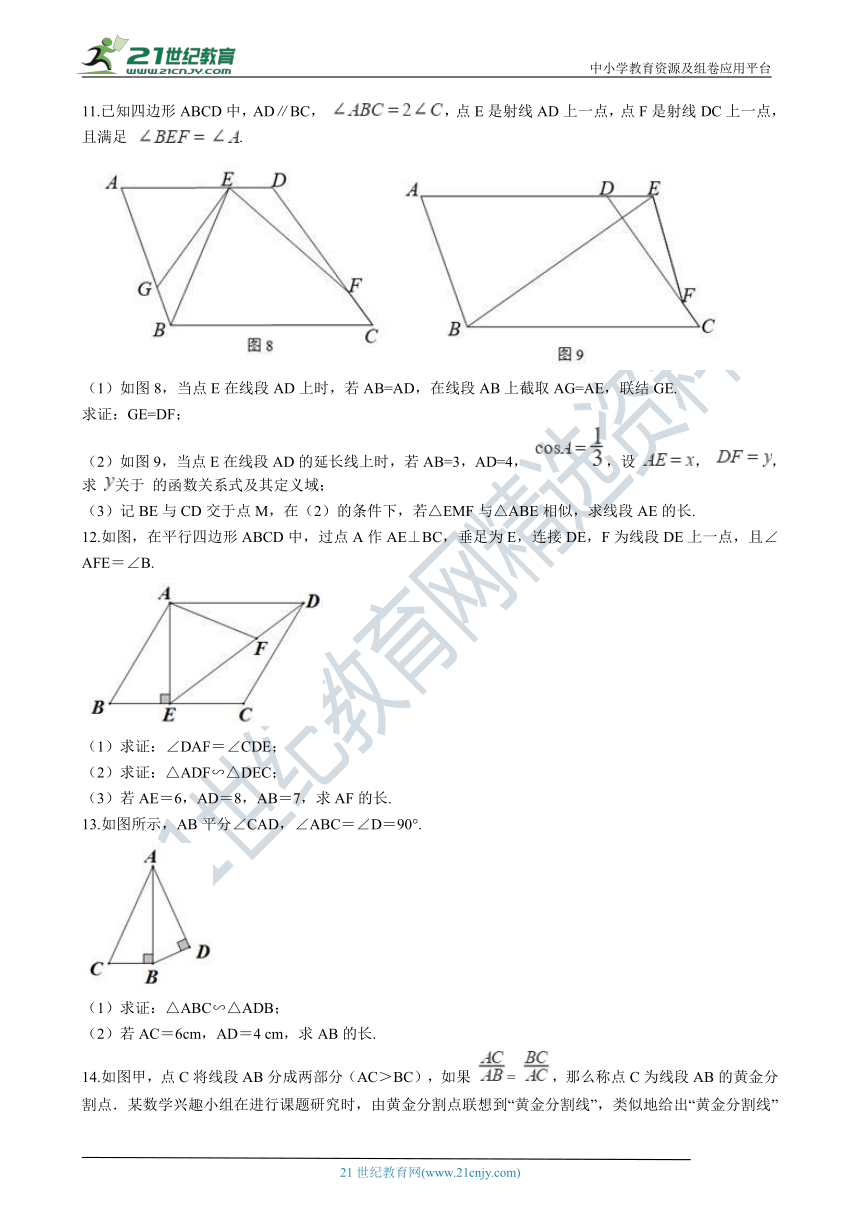
11.已知四边形ABCD中,AD∥BC, ,点E是射线AD上一点,点F是射线DC上一点,且满足 . 【版权所有:21教育】
(1)如图8,当点E在线段AD上时,若AB=AD,在线段AB上截取AG=AE,联结GE.
求证:GE=DF;
(2)如图9,当点E在线段AD的延长线上时,若AB=3,AD=4, ,设 , ,求 关于 的函数关系式及其定义域; 21教育网
(3)记BE与CD交于点M,在(2)的条件下,若△EMF与△ABE相似,求线段AE的长.
12.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. 21*cnjy*com
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
13.如图所示,AB平分∠CAD,∠ABC=∠D=90°.
(1)求证:△ABC∽△ADB;
(2)若AC=6cm,AD=4 cm,求AB的长.
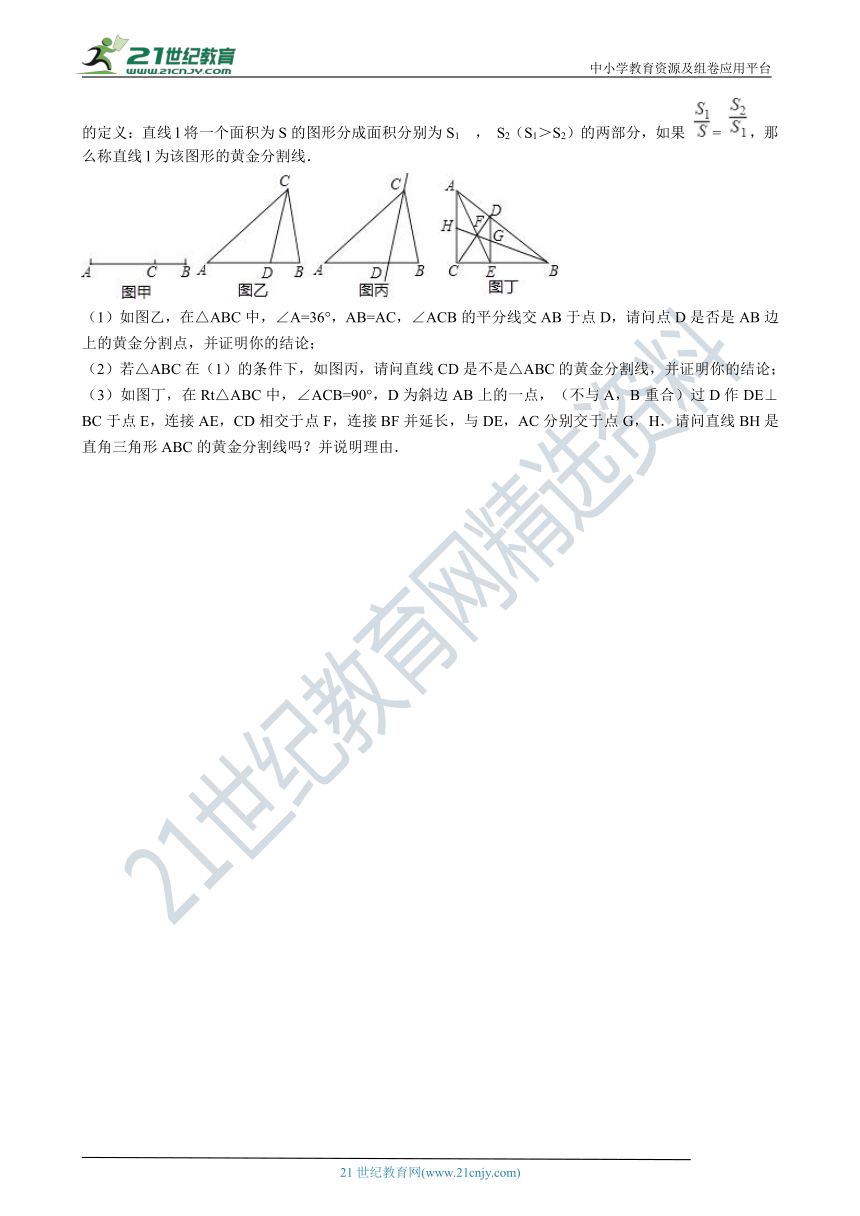
14.如图甲,点C将线段AB分成两部分(AC>BC),如果 = ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 = ,那么称直线l为该图形的黄金分割线.
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
答案解析部分
一、单选题
1. C
解:图中三角形有:△AEG,△ADC,CFG,△CBA,
∵AB∥EF∥DC,AD∥BC
∴△AEG∽△ADC∽CFG∽△CBA
共有6个组合分别为:∴△AEG∽△ADC,△AEG∽CFG,△AEG∽△CBA,△ADC∽CFG,△ADC∽△CBA,CFG∽△CBA。21·世纪*教育网
故答案为:C。
【分析】根据平行于三角形一边的直线截其它两边或两边的延长线,所截的三角形与原三角形相似得出△AEG∽△ADC∽CFG∽△CBA,从而即可得出答案。21教育名师原创作品
2. A
解:A、两直线平行,内错角相等,正确,是真命题;
B、两个锐角的和不一定是钝角,故错误,是假命题;
C、所有的直角三角形不一定相似,故错误,是假命题;
D、正六边形的内角和为720°,故错误,是假命题。
故答案为:A。
【分析】根据平行线的性质、钝角及锐角的定义、相似三角形的判定方法、正多边形的内角和公式即可一一判断得出答案。【出处:21教育名师】
3. B
解:因为 中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故答案为:B.
【分析】利用网格的特点知∠A1B1C1=135°,B选项中有一个角为135°,利用勾股定理分别求出135°角的两邻边的长,可得两邻边之比相等,根据两边对应成比例且夹角相等的两个三角形相似判断即可.
4. C
解:DBAD=DCAE,
A,B,D都可判定 ,
选项C中不是夹这两个角的边,所以不相似.
故答案为:C.
【分析】根据已知条件可证得∠BAC=∠DAE,要证△ABC∽△ADE,因此可以添加另外的两组角对应相等,可对A,C作出判断;还可以添加∠BAC和∠DAE的两边对应成比例,可对C,D作出判断。
5. B
解:A.由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B.由 不能判定△ACD∽△ABC,此选项符合题意;
C.由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D.由AC2=AD?AB,即 ,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故答案为:B.
【分析? △ACD与△ABC中有一公共角A与公共边AC,根据两个三角形相似的判定定理将选项带进去即可排除,选出答案。
6. C
解:∵DE∥AC,
∴△BED∽△BAC,∠EDA=∠DAC,
∵∠1=∠2,
∴△ADE∽△CAD,
∵DE∥AC,
∴∠2=∠EDB,
∵∠1=∠2,
∴∠1=∠EDB,
∵∠B=∠B,
∴△BDE∽△BAD,
∴△ABD∽△CBA,
故答案为:C.
【分析】根据”两角对应相等,两三角形相似“可判断出图中的相似三角形共有4对。
7. B
解:黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,21cnjy.com
故答案为:B.
【分析】黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,21·cn·jy·com
二、填空题
8. ∠B=∠E(答案不唯一)
解:∵ = , ∠B=∠E ∴ △ABC ∽△ADE 故答案为:∠B=∠E www.21-cn-jy.com
【分析】根据已知条件,两边对应成比例,因此添加这两边的夹角相等即可证得△ABC ∽△ADE。
9. ∠ACD=∠B(答案不唯一).
解:△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.理由如下:
∵∠A=∠A,∠ACD=∠B,∴△ACD∽△ABC.
故答案为:∠ACD=∠B(答案不唯一).
【分析】开放性的命题,答案不唯一:由图形可知:两个三角形中已经具有一个公共角∠A,根据相似三角形的判定方法,可以再添加一个角对应相等,或者夹相等角的两边对应成比例即可。
三、综合题
10. (1)解:如图所示:
(2)解:∵△ACB和△A1C1B都是等边三角形,
∴∠BCQ=∠BA1D=60°,
∵∠A1BD=∠QBC,
∴△BCQ∽△BA1D (3)解:猜想∠BCC1=90°,
∵△ACB和△A1C1B都是等边三角形,
∴∠CBA=∠A1BC1=60°,A1B=C1B,AB=CB,
∴∠ABA1=∠CBC1 ,
在△A1BA和△C1BC中: ,
∴△A1BA≌△C1BC(SAS),
∴∠BCC1=∠BAA1=90°.
解析:(1)利用尺规作图法,分别以点A1,B为圆心,A1B为半径画弧,两弧相交于∠MON内部一点C1 , 连接A1C1 , BC1即可; (2)根据等边三角形的每一个内角都等于60°得出 ∠BCQ=∠BA1D=60°, 根据公共角相等得出 ∠A1BD=∠QBC, 根据有两组角对应相等的三角形相似得出 △BCQ∽△BA1D ; (3) 猜想∠BCC1=90°, 理由如下:根据等边三角形的性质得出 ∠CBA=∠A1BC1=60°,A1B=C1B,AB=CB, 故 ∠ABA1=∠CBC1 , 从而利用SAS判断出 △A1BA≌△C1BC ,根据全等三角形的对应角相等得出 ∠BCC1=∠BAA1=90 °。2·1·c·n·j·y
11. (1)证明:∵ ,
∴ .
∵AD∥BC,
∴ ,
∵ ,
∴ ,
∴ ,
∵AD∥BC,
∴ ,
又 ,
∴ .
∵ ,
∵ ,
∴ .
又AB=AD,AG=AE,
∴BG=ED,
∴ ≌ ,
∴GE=DF.
(2)解:在射线AB上截取AH=AE,联结EH.
∵ , ,
又 ,
∴ .
∵AD∥BC,
∴ , .
∵AH=AE,
∴ ,
又 ,
∴ ,
∴ ,
∴ ∽ .
∴ .
过点H作HP⊥AE,垂足为点P.
∵ , ,
∴ , , ,
∴ .
∵AB=3,AD=4, , ,
∴ ,
∴ .
(3)解:记EH与BC相交于点N.
∵ ∽ , ,
∴ ,或 .
若 ,又 ,矛盾,∴此情况不存在.
若 ,∵ ∽ ,∴ ,
∴ .
∵AD∥BC,
∴ ,
∴ ,
∴ ,
∵AD∥BC,
∴ ,
∴ ,
∴ .
∴线段AE的长为 .
解:(1)由AG=AE,可得, 再根据同旁内角互补和邻补角的定义,可得。从而继而可得, 从而可证≌, 故GE=DF; (2)通过证明两组角对应相等得到∽, 得到, 设出, 表达出AP、PH、PE、EH,从而可表达出DF,即y; (3)若△EMF与△ABE相似,有对应角相等,从?得出矛盾,可知不存在,当时能得, 根据AD∥BC能得, 代入可求得线段AE长。【来源:21·世纪·教育·网】
12. (1)证明:∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵∠AFE=∠B,∴∠AFE=∠ADC
∵∠AFE=∠1+∠2,∠ADC=∠3+∠2
∴∠1+∠2=∠3+∠2,即∠1=∠3
∴∠DAF=∠CDE
(2)证明:∵四边形ABCD是平行四边形
∴AD∥BC,∴∠2=∠4
由(1)得∠1=∠3?? ∴△ADF∽△DEC
(3)解:∵AE⊥BC,∴AE⊥AD
∴DE=
由上可得△ADF∽△DEC,CD=AB=7
∴
∴
∴AF=
解:(1)由平行四边形对角相等可知:∠AFE=∠B=∠ADC;由三角形的一个外角等于与它不相邻的两个内角和可知∠AFE=∠ADF+DAF,即可得∠DAF=∠CDE; (2)利用对应两角相等的两个三角形相似即可得证; (3)利用勾股定理可求出DE长,再由(2)中已证的相似三角形的性质即可求出AF长。
13. (1)证明:∵AB平分∠CAD
∴∠1=∠2
∵∠ABC=∠D=90o
∴△ABC∽△ADB
(2)解:由(1)得△ABC∽△ADB
∴ ,
即
∴ .
解:(1)由两组角对应相等的两个三角形相似即可证明; (2)由(1)中已证的相似三角形性质可找出AC、AD、AB的关系,代入数值即可求出AB。
14.(1)解:点D是AB边上的黄金分割点.理由如下:
∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵CD是角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠ACD,
∴AD=CD,
∵∠CDB=180°﹣∠B﹣∠BCD=72°,
∴∠CDB=∠B,
∴BC=CD,
∴BC=AD.
在△BCD与△BCA中,∠B=∠B,∠BCD=∠A=36°,
∴△BCD∽△BAC,
∴ ,
∴ ,
∴点D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.理由如下:
证明:设△ABC中,AB边上的高为h,则S△ABC= ?AB?h,S△ACD= ?AD?h,S△BCD= ?BD?h,
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
由(1)知,点D是AB边上的黄金分割点,
∴ ,???????????????????????????????????
∴S△ACD:S△ABC=S△BCD:S△ACD ,
∴CD是△ABC的黄金分割线.
(3)解:直线BH不是△ABC的黄金分割线.理由如下:
∵DE∥AC,
∴ , ,
∴ , ,
∴ ,
∴AH2=HC2 ,
∴AH=HC,
∴S△BHA=S△BHC= S△ABC ,
∴BH不是△ABC的黄金分割线.
解:(1)根据等边对等角得出∠B=∠ACB=72°,根据角平分线的定义及等量代换得出∠A=∠ACD,进而根据等角对等边得出AD=CD,BC=CD,从而得出BC=AD.然后判断出△BCD∽△BAC,根据相似三角形对应边成比例得出=,从而得出=,从而得出结论点D是AB边上的黄金分割点; (2)设△ABC中,AB边上的高为h,根据三角形的面积公式,则S△ABC=?? AB?h,S△ACD=?AD?h,S△BCD=?? BD?h,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故=,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD , 从而得出结论; (3)直线BH不是△ABC的黄金分割线.理由如下:根据平行线分线段成比例定理得出AH2=HC2 , 故AH=HC,从而S△BHA=S△BHC=?S△ABC , 得出结论BH不是△ABC的黄金分割线.
一、单选题
1.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(?? )
A.?3对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?8对
2.下列命题中,是真命题的是(?? )
A.?两直线平行,内错角相等????????????????????????????????????B.?两个锐角的和是钝角 C.?直角三角形都相似??????????????????????????????????????????????D.?正六边形的内角和为360°21世纪教育网版权所有
3.如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ??)
A.??????????????????B.??????????????????C.??????????????????D.?
4.如图,如果∠BAD=∠CAE,那么添加下列一个条件后,仍不能确定△ABC∽△ADE的是(?? )
A.?∠B=∠D???????????????????????B.?∠C=∠AED???????????????????????C.?= ???????????????????????D.?=
5.如图,下列条件中不能判定△ACD∽△ABC的是(??? )
A.?∠ADC=∠ACB???????????????????B.????????????????????C.?∠ACD=∠B???????????????????D.?AC2=AD?AB
6.如图,∠1=∠2,DE∥AC,则图中的相似三角形有(?? )
A.?2对???????????????????????????????????????B.?3对???????????????????????????????????????C.?4对???????????????????????????????????????D.?5对
7.“黄金分割”是一条举世公认的美学定律. 例如在摄影中,人们常依据黄金分割进行构图,使画面整体和谐. 目前,照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗,按照黄金分割的原则,应该使小狗置于画面中的位置(?? )www-2-1-cnjy-com
A.?①?????????????????????????????????????????B.?②?????????????????????????????????????????C.?③?????????????????????????????????????????D.?④
二、填空题
8.如图,在△ABC和△ADE中, = ,要使△ABC 和 △ADE相似,还需要添加一个条件,这个条件是________ 2-1-c-n-j-y
9.如图,若使△ACD∽△ABC,需添加的一个条件是________.
三、综合题
10.已知∠MON=90°,等边三角形ABC的一个顶点B是射线ON上的一定点,顶点A与点O重合,顶点C在∠MON内部 21*cnjy*com
(1)当点A在射线OM上移动到A1时,连接A1B,请在∠MON内部作出以A1B为一边的等边三角形A1BC1(保留作图痕迹,不写作法); 【来源:21cnj*y.co*m】
(2)设A1B与OC交于点Q,BC的延长线与A1C1交于点D.求证:△BCQ∽△BA1D;
(3)连接CC1 , 试猜想∠BCC1为多少度,并证明你的猜想.
11.已知四边形ABCD中,AD∥BC, ,点E是射线AD上一点,点F是射线DC上一点,且满足 . 【版权所有:21教育】
(1)如图8,当点E在线段AD上时,若AB=AD,在线段AB上截取AG=AE,联结GE.
求证:GE=DF;
(2)如图9,当点E在线段AD的延长线上时,若AB=3,AD=4, ,设 , ,求 关于 的函数关系式及其定义域; 21教育网
(3)记BE与CD交于点M,在(2)的条件下,若△EMF与△ABE相似,求线段AE的长.
12.如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. 21*cnjy*com
(1)求证:∠DAF=∠CDE;
(2)求证:△ADF∽△DEC;
(3)若AE=6,AD=8,AB=7,求AF的长.
13.如图所示,AB平分∠CAD,∠ABC=∠D=90°.
(1)求证:△ABC∽△ADB;
(2)若AC=6cm,AD=4 cm,求AB的长.
14.如图甲,点C将线段AB分成两部分(AC>BC),如果 = ,那么称点C为线段AB的黄金分割点.某数学兴趣小组在进行课题研究时,由黄金分割点联想到“黄金分割线”,类似地给出“黄金分割线”的定义:直线l将一个面积为S的图形分成面积分别为S1 , S2(S1>S2)的两部分,如果 = ,那么称直线l为该图形的黄金分割线.
(1)如图乙,在△ABC中,∠A=36°,AB=AC,∠ACB的平分线交AB于点D,请问点D是否是AB边上的黄金分割点,并证明你的结论;
(2)若△ABC在(1)的条件下,如图丙,请问直线CD是不是△ABC的黄金分割线,并证明你的结论;
(3)如图丁,在Rt△ABC中,∠ACB=90°,D为斜边AB上的一点,(不与A,B重合)过D作DE⊥BC于点E,连接AE,CD相交于点F,连接BF并延长,与DE,AC分别交于点G,H.请问直线BH是直角三角形ABC的黄金分割线吗?并说明理由.
答案解析部分
一、单选题
1. C
解:图中三角形有:△AEG,△ADC,CFG,△CBA,
∵AB∥EF∥DC,AD∥BC
∴△AEG∽△ADC∽CFG∽△CBA
共有6个组合分别为:∴△AEG∽△ADC,△AEG∽CFG,△AEG∽△CBA,△ADC∽CFG,△ADC∽△CBA,CFG∽△CBA。21·世纪*教育网
故答案为:C。
【分析】根据平行于三角形一边的直线截其它两边或两边的延长线,所截的三角形与原三角形相似得出△AEG∽△ADC∽CFG∽△CBA,从而即可得出答案。21教育名师原创作品
2. A
解:A、两直线平行,内错角相等,正确,是真命题;
B、两个锐角的和不一定是钝角,故错误,是假命题;
C、所有的直角三角形不一定相似,故错误,是假命题;
D、正六边形的内角和为720°,故错误,是假命题。
故答案为:A。
【分析】根据平行线的性质、钝角及锐角的定义、相似三角形的判定方法、正多边形的内角和公式即可一一判断得出答案。【出处:21教育名师】
3. B
解:因为 中有一个角是135°,选项中,有135°角的三角形只有B,且满足两边成比例夹角相等,
故答案为:B.
【分析】利用网格的特点知∠A1B1C1=135°,B选项中有一个角为135°,利用勾股定理分别求出135°角的两邻边的长,可得两邻边之比相等,根据两边对应成比例且夹角相等的两个三角形相似判断即可.
4. C
解:DBAD=DCAE,
A,B,D都可判定 ,
选项C中不是夹这两个角的边,所以不相似.
故答案为:C.
【分析】根据已知条件可证得∠BAC=∠DAE,要证△ABC∽△ADE,因此可以添加另外的两组角对应相等,可对A,C作出判断;还可以添加∠BAC和∠DAE的两边对应成比例,可对C,D作出判断。
5. B
解:A.由∠ADC=∠ACB,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
B.由 不能判定△ACD∽△ABC,此选项符合题意;
C.由∠ACD=∠B,∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
D.由AC2=AD?AB,即 ,且∠A=∠A可得△ACD∽△ABC,此选项不符合题意;
故答案为:B.
【分析? △ACD与△ABC中有一公共角A与公共边AC,根据两个三角形相似的判定定理将选项带进去即可排除,选出答案。
6. C
解:∵DE∥AC,
∴△BED∽△BAC,∠EDA=∠DAC,
∵∠1=∠2,
∴△ADE∽△CAD,
∵DE∥AC,
∴∠2=∠EDB,
∵∠1=∠2,
∴∠1=∠EDB,
∵∠B=∠B,
∴△BDE∽△BAD,
∴△ABD∽△CBA,
故答案为:C.
【分析】根据”两角对应相等,两三角形相似“可判断出图中的相似三角形共有4对。
7. B
解:黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,21cnjy.com
故答案为:B.
【分析】黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618,观察图中的位置可知应该使小狗置于画面中②的位置,21·cn·jy·com
二、填空题
8. ∠B=∠E(答案不唯一)
解:∵ = , ∠B=∠E ∴ △ABC ∽△ADE 故答案为:∠B=∠E www.21-cn-jy.com
【分析】根据已知条件,两边对应成比例,因此添加这两边的夹角相等即可证得△ABC ∽△ADE。
9. ∠ACD=∠B(答案不唯一).
解:△ACD∽△ABC,需添加的一个条件是∠ACD=∠B.理由如下:
∵∠A=∠A,∠ACD=∠B,∴△ACD∽△ABC.
故答案为:∠ACD=∠B(答案不唯一).
【分析】开放性的命题,答案不唯一:由图形可知:两个三角形中已经具有一个公共角∠A,根据相似三角形的判定方法,可以再添加一个角对应相等,或者夹相等角的两边对应成比例即可。
三、综合题
10. (1)解:如图所示:
(2)解:∵△ACB和△A1C1B都是等边三角形,
∴∠BCQ=∠BA1D=60°,
∵∠A1BD=∠QBC,
∴△BCQ∽△BA1D (3)解:猜想∠BCC1=90°,
∵△ACB和△A1C1B都是等边三角形,
∴∠CBA=∠A1BC1=60°,A1B=C1B,AB=CB,
∴∠ABA1=∠CBC1 ,
在△A1BA和△C1BC中: ,
∴△A1BA≌△C1BC(SAS),
∴∠BCC1=∠BAA1=90°.
解析:(1)利用尺规作图法,分别以点A1,B为圆心,A1B为半径画弧,两弧相交于∠MON内部一点C1 , 连接A1C1 , BC1即可; (2)根据等边三角形的每一个内角都等于60°得出 ∠BCQ=∠BA1D=60°, 根据公共角相等得出 ∠A1BD=∠QBC, 根据有两组角对应相等的三角形相似得出 △BCQ∽△BA1D ; (3) 猜想∠BCC1=90°, 理由如下:根据等边三角形的性质得出 ∠CBA=∠A1BC1=60°,A1B=C1B,AB=CB, 故 ∠ABA1=∠CBC1 , 从而利用SAS判断出 △A1BA≌△C1BC ,根据全等三角形的对应角相等得出 ∠BCC1=∠BAA1=90 °。2·1·c·n·j·y
11. (1)证明:∵ ,
∴ .
∵AD∥BC,
∴ ,
∵ ,
∴ ,
∴ ,
∵AD∥BC,
∴ ,
又 ,
∴ .
∵ ,
∵ ,
∴ .
又AB=AD,AG=AE,
∴BG=ED,
∴ ≌ ,
∴GE=DF.
(2)解:在射线AB上截取AH=AE,联结EH.
∵ , ,
又 ,
∴ .
∵AD∥BC,
∴ , .
∵AH=AE,
∴ ,
又 ,
∴ ,
∴ ,
∴ ∽ .
∴ .
过点H作HP⊥AE,垂足为点P.
∵ , ,
∴ , , ,
∴ .
∵AB=3,AD=4, , ,
∴ ,
∴ .
(3)解:记EH与BC相交于点N.
∵ ∽ , ,
∴ ,或 .
若 ,又 ,矛盾,∴此情况不存在.
若 ,∵ ∽ ,∴ ,
∴ .
∵AD∥BC,
∴ ,
∴ ,
∴ ,
∵AD∥BC,
∴ ,
∴ ,
∴ .
∴线段AE的长为 .
解:(1)由AG=AE,可得, 再根据同旁内角互补和邻补角的定义,可得。从而继而可得, 从而可证≌, 故GE=DF; (2)通过证明两组角对应相等得到∽, 得到, 设出, 表达出AP、PH、PE、EH,从而可表达出DF,即y; (3)若△EMF与△ABE相似,有对应角相等,从?得出矛盾,可知不存在,当时能得, 根据AD∥BC能得, 代入可求得线段AE长。【来源:21·世纪·教育·网】
12. (1)证明:∵四边形ABCD是平行四边形
∴∠B=∠ADC
∵∠AFE=∠B,∴∠AFE=∠ADC
∵∠AFE=∠1+∠2,∠ADC=∠3+∠2
∴∠1+∠2=∠3+∠2,即∠1=∠3
∴∠DAF=∠CDE
(2)证明:∵四边形ABCD是平行四边形
∴AD∥BC,∴∠2=∠4
由(1)得∠1=∠3?? ∴△ADF∽△DEC
(3)解:∵AE⊥BC,∴AE⊥AD
∴DE=
由上可得△ADF∽△DEC,CD=AB=7
∴
∴
∴AF=
解:(1)由平行四边形对角相等可知:∠AFE=∠B=∠ADC;由三角形的一个外角等于与它不相邻的两个内角和可知∠AFE=∠ADF+DAF,即可得∠DAF=∠CDE; (2)利用对应两角相等的两个三角形相似即可得证; (3)利用勾股定理可求出DE长,再由(2)中已证的相似三角形的性质即可求出AF长。
13. (1)证明:∵AB平分∠CAD
∴∠1=∠2
∵∠ABC=∠D=90o
∴△ABC∽△ADB
(2)解:由(1)得△ABC∽△ADB
∴ ,
即
∴ .
解:(1)由两组角对应相等的两个三角形相似即可证明; (2)由(1)中已证的相似三角形性质可找出AC、AD、AB的关系,代入数值即可求出AB。
14.(1)解:点D是AB边上的黄金分割点.理由如下:
∵AB=AC,∠A=36°,
∴∠B=∠ACB=72°,
∵CD是角平分线,
∴∠ACD=∠BCD=36°,
∴∠A=∠ACD,
∴AD=CD,
∵∠CDB=180°﹣∠B﹣∠BCD=72°,
∴∠CDB=∠B,
∴BC=CD,
∴BC=AD.
在△BCD与△BCA中,∠B=∠B,∠BCD=∠A=36°,
∴△BCD∽△BAC,
∴ ,
∴ ,
∴点D是AB边上的黄金分割点.
(2)直线CD是△ABC的黄金分割线.理由如下:
证明:设△ABC中,AB边上的高为h,则S△ABC= ?AB?h,S△ACD= ?AD?h,S△BCD= ?BD?h,
∴S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,
由(1)知,点D是AB边上的黄金分割点,
∴ ,???????????????????????????????????
∴S△ACD:S△ABC=S△BCD:S△ACD ,
∴CD是△ABC的黄金分割线.
(3)解:直线BH不是△ABC的黄金分割线.理由如下:
∵DE∥AC,
∴ , ,
∴ , ,
∴ ,
∴AH2=HC2 ,
∴AH=HC,
∴S△BHA=S△BHC= S△ABC ,
∴BH不是△ABC的黄金分割线.
解:(1)根据等边对等角得出∠B=∠ACB=72°,根据角平分线的定义及等量代换得出∠A=∠ACD,进而根据等角对等边得出AD=CD,BC=CD,从而得出BC=AD.然后判断出△BCD∽△BAC,根据相似三角形对应边成比例得出=,从而得出=,从而得出结论点D是AB边上的黄金分割点; (2)设△ABC中,AB边上的高为h,根据三角形的面积公式,则S△ABC=?? AB?h,S△ACD=?AD?h,S△BCD=?? BD?h,故S△ACD:S△ABC=AD:AB,S△BCD:S△ACD=BD:AD,由(1)知,点D是AB边上的黄金分割点,故=,根据等量代换得S△ACD:S△ABC=S△BCD:S△ACD , 从而得出结论; (3)直线BH不是△ABC的黄金分割线.理由如下:根据平行线分线段成比例定理得出AH2=HC2 , 故AH=HC,从而S△BHA=S△BHC=?S△ABC , 得出结论BH不是△ABC的黄金分割线.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
