4.7 相似三角形的性质 同步练习(解析版)
文档属性
| 名称 | 4.7 相似三角形的性质 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 16:55:38 | ||
图片预览



文档简介
初中数学北师大版九年级上学期 第四章 4.7 相似三角形的性质
一、单选题
1.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是(??? ) 21cnjy.com
A.?3:5???????????????????????????????????B.?9:25???????????????????????????????????C.?5:3???????????????????????????????????D.?25:9
2.把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ?????;若边长扩大5倍,则面积扩大????? 。(?? ) 2·1·c·n·j·y
A.?5倍,10倍?????????????????????B.?10倍,25倍?????????????????????C.?倍,25倍?????????????????????D.?25倍,25倍
3.已知 ∽ ,AB=8,A`B`=6,则 (? )
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.?3?????????????????????????????????????????D.?
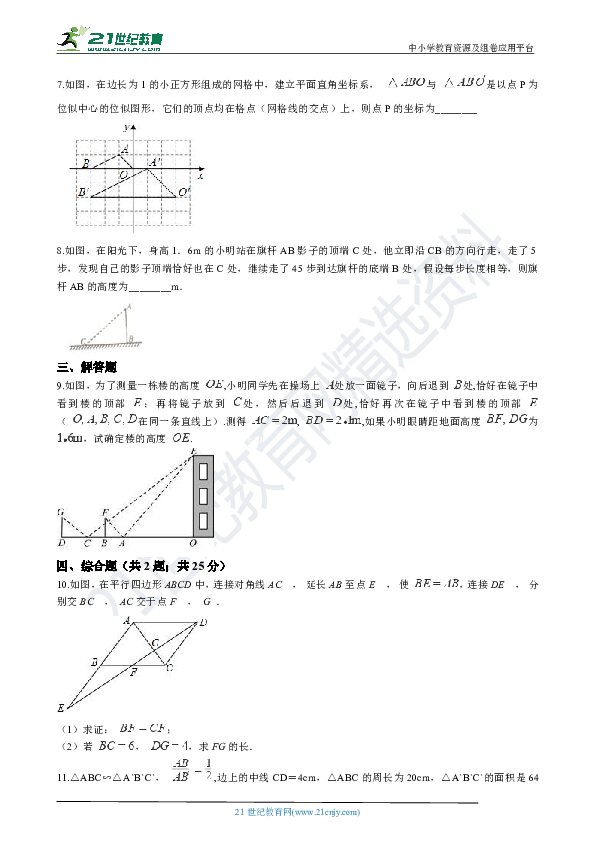
4.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(??? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
5.如图,在正方形ABCD的对角线AC上取一点E . 使得 ,连接BE并延长BE到F , 使 ,BF与CD相交于点H , 若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有(??? ) 2-1-c-n-j-y
A.?①②③???????????????????????????????B.?①②③④???????????????????????????????C.?①②④???????????????????????????????D.?①③④
二、填空题
6.三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为________cm. 21·世纪*教育网
7.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系, 与 是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为________
8.如图,在阳光下,身高1.6m的小明站在旗杆AB影子的顶端C处,他立即沿CB的方向行走,走了5步,发现自己的影子顶端恰好也在C处,继续走了45步到达旗杆的底端B处,假设每步长度相等,则旗杆AB的高度为________m. 【来源:21cnj*y.co*m】
三、解答题
9.如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 . 【版权所有:21教育】
四、综合题(共2题;共25分)
10.如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G . 21教育名师原创作品
(1)求证: ;
(2)若 , ,求FG的长.
11.△ABC∽△A`B`C`, ,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2 , 求: 21*cnjy*com
(1)A`B`边上的中线C`D`的长;
(2)△A`B`C`的周长
(3)△ABC的面积
答案解析部分
一、单选题
1. C
解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD:A′D′=10:6=5:3.
故答案为:C.
【分析】根据相似三角形的周长之比、对应中线的比都等于相似比即可得出答案。
2. C
解:因为面积扩大了5倍,所以边长扩大了 倍,边长扩大5倍,则面积扩大25倍.
故答案为:C.
【分析】根据相似三角形面积的比等于相似比的平方,即可得出答案。
3. B
解:∵ ∽ , ∴, ∵ AB=8,A'B'=6, ∴. 故答案为:B。 【出处:21教育名师】
【分析】根据相似三角形对应边成比例即可得出答案。
4. C
解:∵△ABO∽△CDO,
∴ = ,
∵BO=6,DO=3,CD=2,
∴ = ,
解得:AB=4.
故答案为:C.
【分析】根据相似三角形对应边成比例得出 = ,根据比例式即可求出AB的长。
5. A
解:证明:①∵四边形ABCD是正方形,
∴ , , .
在 和 中,
,
∴ ,
∴ ,故①符合题意;
②在EF上取一点G , 使 ,连结CG ,
∵ ,
∴ .
∴ ,
∵ ,
∴ ,
∴ .
∵ ,
∴ ,
∴ .
∵ ,
∴ 是等边三角形.
∴ , ,
∴ ,
∴ .
在 和 中,
,
∴ ,
∴ .
∵ ,
∴ ,故②符合题意;
③过D作 交于M ,
根据勾股定理求出 ,
由面积公式得: ,
∴ ,
∵ , ,
∴ , ,
∴
∴ ,故③符合题意;
④在 中, ,
∵ 是等边三角形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,故④不符合题意;
综上,正确的结论有①②③,
故答案为:A .
【分析】根据全等三角形和相似三角形、矩形的性质,进行证明,可得出正确的结论。
二、填空题
6. 12+8
解:连接AC交BD于K,
根据菱形的性质OA和HG互相垂直平分,又∵∠AOB=90°得HG∥KO,又OG∥KH,∴则四边形HKOG为平行四边形,则OK=HG=2。∠CDB+∠HDB=∠ADH+∠HDB=90°。又OH=OC,则△HOC为等腰直角△,∠CHO=45°,∵HG=KO=2,∠BOC=∠CAO,∠OCK=∠ACK,∴△OCK=△ACK, ,则BE=2OA= ,AB= ?,则△ABE周长为BE+2AB= 。21世纪教育网版权所有
在故答案为: ?。
【分析】利用四边形HKOG是平行四边形得KO=2,由△COH是等腰直角三角形,得各边之比确定,本题关键是抓住A、H、C三点共线,找三角形相似,利用相似比可求OA的长,OA求出,∵△ABE是等腰直角三角形,则其他各边可求,得其周长。21教育网
7.
解:根据位似图形的性质“位似图形对应点连线的交点是位似中心”,
连接 并延长, 并延长, 与 的交点即为位似中心P点,由图可知 、B、P在一条直线上,则P点横坐标为-3,【来源:21·世纪·教育·网】
由图可得 和 的位似比为 , ,
所以 ,
解得PB=2,
所以P点纵坐标为 ,
即P点坐标为 .
故答案为:
【分析】由题意根据位似图形的性质特点,位似图形对应点连线的交点是位似中心,根据位似比一定,即可求出点P的坐标。 ?www-2-1-cnjy-com
8. 16
解:根据题意可知,, 解得,AB=16. 故答案为:16。 【分析】根据题意,利用相似三角形的性质进行作答即可,相似三角形的对应边成比例,即可得到AB的长度。21*cnjy*com
三、解答题
9. 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,??
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
解:根据光的反射定律作出相关光路图,因为GF∥AC,利用三角形相似分别列比例式。因为根据平面镜成像特点,像和物是等大的,找出有关相等的线段,进行一系列相关的等量代换,使关系式用用已知线段表示,代入已知数据,得出楼的高度。www.21-cn-jy.com
四、综合题
10. (1)证明: 四边形ABCD是平行四边形,
, ,
,
∴ ,
∵BE=AB,AE=AB+BE,
,
,
(2)解: 四边形ABCD是平行四边形,
,
,
,即 ,
解得, .
解:(1)根据平行四边形的性质,即可证明△EBF∽△EAD,根据相似的性质从而得到答案。 (2)根据平行四边形的性质证明△FGC∽△DGA,根据相似三角形的性质即可得到答案。
11.(1)解:∵△ABC∽△A′B′C′, ,AB边上的中线CD=4cm,
∴ = ,
∴C′D′=4cm×2=8cm,
∴A′B′边上的中线C′D′的长为8cm
(2)解:∵△ABC∽△A′B′C′, ,△ABC的周长为20cm,
∴ ,
∴C△A′B′C′=20cm×2=40cm,
∴△A′B′C′的周长为40cm
(3)解:∵△ABC∽△A′B′C′, ,△A′B′C′的面积是64cm2 ,
∴ ,
∴S△ABC=64cm2÷4=16cm2 ,
∴△ABC的面积是16cm2.
解:(1)根据相似三角形对应边的中线的比等于相似比可得方程求解; (2)根据相似三角形周长的比等于相似比可得方程求解; (3)根据相似三角形面积的比等于相似比的平方即可求解。21·cn·jy·com
一、单选题
1.已知△ABC∽△A'B'C',AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的周长比是(??? ) 21cnjy.com
A.?3:5???????????????????????????????????B.?9:25???????????????????????????????????C.?5:3???????????????????????????????????D.?25:9
2.把一个三角形变成和它相似的三角形,若面积扩大5倍,则边长扩大 ?????;若边长扩大5倍,则面积扩大????? 。(?? ) 2·1·c·n·j·y
A.?5倍,10倍?????????????????????B.?10倍,25倍?????????????????????C.?倍,25倍?????????????????????D.?25倍,25倍
3.已知 ∽ ,AB=8,A`B`=6,则 (? )
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.?3?????????????????????????????????????????D.?
4.如图,△ABO∽△CDO,若BO=6,DO=3,CD=2,则AB的长是(??? )
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
5.如图,在正方形ABCD的对角线AC上取一点E . 使得 ,连接BE并延长BE到F , 使 ,BF与CD相交于点H , 若 ,有下列结论:① ;② ;③ ;④ .则其中正确的结论有(??? ) 2-1-c-n-j-y
A.?①②③???????????????????????????????B.?①②③④???????????????????????????????C.?①②④???????????????????????????????D.?①③④
二、填空题
6.三个形状大小相同的菱形按如图所示方式摆放,已知∠AOB=∠AOE=90°,菱形的较短对角线长为2cm.若点C落在AH的延长线上,则△ABE的周长为________cm. 21·世纪*教育网
7.如图,在边长为1的小正方形组成的网格中,建立平面直角坐标系, 与 是以点P为位似中心的位似图形,它们的顶点均在格点(网格线的交点)上,则点P的坐标为________
8.如图,在阳光下,身高1.6m的小明站在旗杆AB影子的顶端C处,他立即沿CB的方向行走,走了5步,发现自己的影子顶端恰好也在C处,继续走了45步到达旗杆的底端B处,假设每步长度相等,则旗杆AB的高度为________m. 【来源:21cnj*y.co*m】
三、解答题
9.如图,为了测量一栋楼的高度 ,小明同学先在操场上 处放一面镜子,向后退到 处,恰好在镜子中看到楼的顶部 ;再将镜子放到 处,然后后退到 处,恰好再次在镜子中看到楼的顶部 ( 在同一条直线上).测得 , ,如果小明眼睛距地面高度 为 ,试确定楼的高度 . 【版权所有:21教育】
四、综合题(共2题;共25分)
10.如图,在平行四边形ABCD中,连接对角线AC , 延长AB至点E , 使 ,连接DE , 分别交BC , AC交于点F , G . 21教育名师原创作品
(1)求证: ;
(2)若 , ,求FG的长.
11.△ABC∽△A`B`C`, ,边上的中线CD=4cm,△ABC的周长为20cm,△A`B`C`的面积是64 cm2 , 求: 21*cnjy*com
(1)A`B`边上的中线C`D`的长;
(2)△A`B`C`的周长
(3)△ABC的面积
答案解析部分
一、单选题
1. C
解:∵△ABC∽△A'B'C',AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴△ABC与△A'B'C'的周长比=AD:A′D′=10:6=5:3.
故答案为:C.
【分析】根据相似三角形的周长之比、对应中线的比都等于相似比即可得出答案。
2. C
解:因为面积扩大了5倍,所以边长扩大了 倍,边长扩大5倍,则面积扩大25倍.
故答案为:C.
【分析】根据相似三角形面积的比等于相似比的平方,即可得出答案。
3. B
解:∵ ∽ , ∴, ∵ AB=8,A'B'=6, ∴. 故答案为:B。 【出处:21教育名师】
【分析】根据相似三角形对应边成比例即可得出答案。
4. C
解:∵△ABO∽△CDO,
∴ = ,
∵BO=6,DO=3,CD=2,
∴ = ,
解得:AB=4.
故答案为:C.
【分析】根据相似三角形对应边成比例得出 = ,根据比例式即可求出AB的长。
5. A
解:证明:①∵四边形ABCD是正方形,
∴ , , .
在 和 中,
,
∴ ,
∴ ,故①符合题意;
②在EF上取一点G , 使 ,连结CG ,
∵ ,
∴ .
∴ ,
∵ ,
∴ ,
∴ .
∵ ,
∴ ,
∴ .
∵ ,
∴ 是等边三角形.
∴ , ,
∴ ,
∴ .
在 和 中,
,
∴ ,
∴ .
∵ ,
∴ ,故②符合题意;
③过D作 交于M ,
根据勾股定理求出 ,
由面积公式得: ,
∴ ,
∵ , ,
∴ , ,
∴
∴ ,故③符合题意;
④在 中, ,
∵ 是等边三角形,
∴ ,
∵ ,
∴ ,
∴ ,
∴ ,故④不符合题意;
综上,正确的结论有①②③,
故答案为:A .
【分析】根据全等三角形和相似三角形、矩形的性质,进行证明,可得出正确的结论。
二、填空题
6. 12+8
解:连接AC交BD于K,
根据菱形的性质OA和HG互相垂直平分,又∵∠AOB=90°得HG∥KO,又OG∥KH,∴则四边形HKOG为平行四边形,则OK=HG=2。∠CDB+∠HDB=∠ADH+∠HDB=90°。又OH=OC,则△HOC为等腰直角△,∠CHO=45°,∵HG=KO=2,∠BOC=∠CAO,∠OCK=∠ACK,∴△OCK=△ACK, ,则BE=2OA= ,AB= ?,则△ABE周长为BE+2AB= 。21世纪教育网版权所有
在故答案为: ?。
【分析】利用四边形HKOG是平行四边形得KO=2,由△COH是等腰直角三角形,得各边之比确定,本题关键是抓住A、H、C三点共线,找三角形相似,利用相似比可求OA的长,OA求出,∵△ABE是等腰直角三角形,则其他各边可求,得其周长。21教育网
7.
解:根据位似图形的性质“位似图形对应点连线的交点是位似中心”,
连接 并延长, 并延长, 与 的交点即为位似中心P点,由图可知 、B、P在一条直线上,则P点横坐标为-3,【来源:21·世纪·教育·网】
由图可得 和 的位似比为 , ,
所以 ,
解得PB=2,
所以P点纵坐标为 ,
即P点坐标为 .
故答案为:
【分析】由题意根据位似图形的性质特点,位似图形对应点连线的交点是位似中心,根据位似比一定,即可求出点P的坐标。 ?www-2-1-cnjy-com
8. 16
解:根据题意可知,, 解得,AB=16. 故答案为:16。 【分析】根据题意,利用相似三角形的性质进行作答即可,相似三角形的对应边成比例,即可得到AB的长度。21*cnjy*com
三、解答题
9. 解:设 关于点 的对称点为 ,由光的反射定律知,延长 相交于 ,??
连接 并延长交 于 ,
∥ , ∽ ,
,
即 ,
,
.
答:楼的高度 为32米。
解:根据光的反射定律作出相关光路图,因为GF∥AC,利用三角形相似分别列比例式。因为根据平面镜成像特点,像和物是等大的,找出有关相等的线段,进行一系列相关的等量代换,使关系式用用已知线段表示,代入已知数据,得出楼的高度。www.21-cn-jy.com
四、综合题
10. (1)证明: 四边形ABCD是平行四边形,
, ,
,
∴ ,
∵BE=AB,AE=AB+BE,
,
,
(2)解: 四边形ABCD是平行四边形,
,
,
,即 ,
解得, .
解:(1)根据平行四边形的性质,即可证明△EBF∽△EAD,根据相似的性质从而得到答案。 (2)根据平行四边形的性质证明△FGC∽△DGA,根据相似三角形的性质即可得到答案。
11.(1)解:∵△ABC∽△A′B′C′, ,AB边上的中线CD=4cm,
∴ = ,
∴C′D′=4cm×2=8cm,
∴A′B′边上的中线C′D′的长为8cm
(2)解:∵△ABC∽△A′B′C′, ,△ABC的周长为20cm,
∴ ,
∴C△A′B′C′=20cm×2=40cm,
∴△A′B′C′的周长为40cm
(3)解:∵△ABC∽△A′B′C′, ,△A′B′C′的面积是64cm2 ,
∴ ,
∴S△ABC=64cm2÷4=16cm2 ,
∴△ABC的面积是16cm2.
解:(1)根据相似三角形对应边的中线的比等于相似比可得方程求解; (2)根据相似三角形周长的比等于相似比可得方程求解; (3)根据相似三角形面积的比等于相似比的平方即可求解。21·cn·jy·com
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
