人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题1.4 全称量词与存在量词
文档属性
| 名称 | 人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题1.4 全称量词与存在量词 |  | |
| 格式 | zip | ||
| 文件大小 | 456.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 15:57:36 | ||
图片预览




文档简介
知识
1.全称量词和全称命题
(1)短语“__________”“__________”在逻辑中通常叫做全称量词,并用符号“______”表示,常见的全称量词还有“一切”“每一个”“任给”“所有的”等.
(2)含有____________的命题,叫做全称命题.
(3)全称命题:“对M中任意一个x,有 成立”,可用符号简记为____________.
注意:全称命题含有全称量词,有些全称命题中的全称量词是可以省略的,理解时需要把它补充出来.
2.存在量词和特称命题
(1)短语“__________”“____________”在逻辑中通常叫做存在量词,并用符号“______”表示,常见的存在量词还有“有些”“有一个”“对某个”“有的”等.
(2)含有____________的命题,叫做特称命题.
(3)特称命题:“存在M中的元素x0,有p(x0)成立”,可用符号简记为________________________.
注意:(1)含有存在量词的命题,不管包含的程度多大,都是特称命题.
(2)不管含不含有存在量词,只要在意义上具有“存在”“有一个”等特征的命题都是特征命题.
3.含有一个量词的命题的否定
(1)全称命题 ,它的否定:________________;
(2)特称命题,它的否定:________________.
注意:含有一个量词的命题的否定,是在否定结论的同时,改变量词的属性,即将全称量词改为存在量词,存在量词改为全称量词.
知识参考答案:
1.(1)所有的 任意一个 ? (2)全称量词 (3)
2.(1)存在一个 至少有一个 ? (2)存在量词 (3)?x0∈M,p(x0)
3.(1),;(2),
重点
重点
掌握全称量词与存在量词的的意义以及掌握对含有一个量词的命题进行否定的方法
难点
掌握含有量词的命题:全称命题和特称命题真假的判断;明确全称命题的否定是存在命题,存在命题的否定是全称命题
易错
易混淆全称命题与特称命题
1.用量词表示命题
由于叙述的多样性,有些语句不是典型的全称命题或特称命题,但却表达了这两种命题的意思,如果能恰当地引入全称量词或存在量词,即可使题意清晰明了.
全称量词相当于日常语言中“凡”,“所有”,“一切”,“任意一个”等;存在量词相当于日常语言中“存在一个”,“有一个”,“有些”,“至少有一个”,“至多有一个”等.
【例1】用全称量词或存在量词表示下列语句.
(1)不等式x2+x+1>0恒成立;
(2)当x为有理数时,x2+x+1也是有理数;
(3)等式sin(α+β)=sin α+sin β对有些角α,β成立;
(4)方程3x-2y=10有整数解.
(3)存在角α0,β0,使sin(α0+β0)=sin α0+sin β0成立.
(4)存在整数x0,y0,使3x0-2y0=10成立.
【名师点睛】利用相关量词表示命题尤其是全称命题和特称命题,可以更准确地表述命题的含义,这就需要我们对量词及全称命题、特称命题有较好的把握,能够准确体会其意义,并且适当引入量词.
2.全称命题与特称命题的真假判断
(1)判断命题是全称命题还是特称命题,关键是找出命题中含有的量词,隐含量词需依据命题的特征挖掘出来.
(2)①要确定一个全称命题是真命题,需保证该命题对所有的元素都成立;若能举出一个反例说明命题不成立,则该全称命题是假命题.
②要确定一个特称命题是真命题,举出一个例子说明该命题成立即可;若经过逻辑推理得到命题对所有的元素都不成立,则该特称命题是假命题.
【例2】判断下列命题是全称命题还是特称命题,并判断其真假.
(1)对数函数都是单调函数;
(2)至少有一个整数,它既能被11整除,又能被9整除;
(3)?x∈{x|x>0},;
(4)?x0∈Z,log2x0>2.
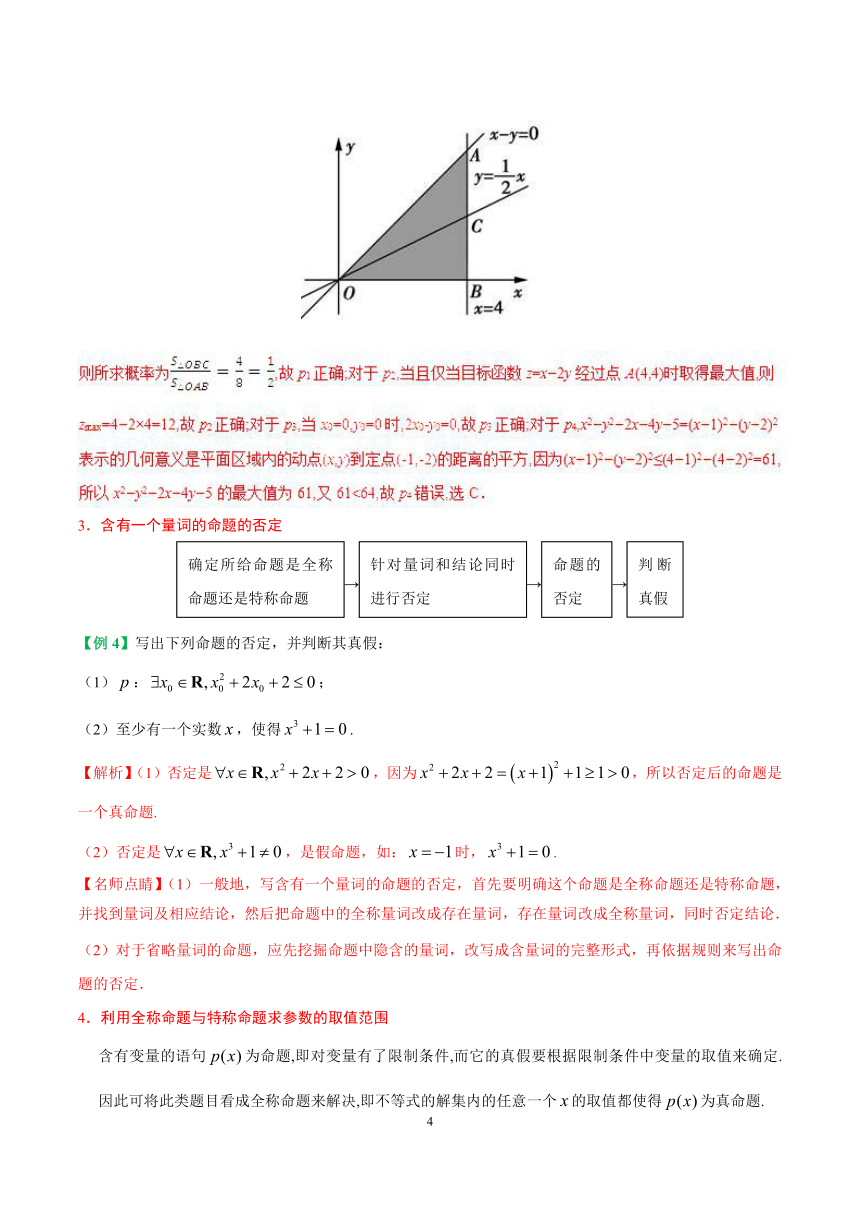
【例3】已知不等式组的解集为D,有下面四个命题:
p1:?(x,y)∈D,2y≤x的概率为; p2:?(x,y)∈D,x+2y的最大值为12;
p3:?(x0,y0)∈D,2x0-y0≤0; p4:?(x,y)∈D,x2+y2+2x+4y+5的最大值为64.
其中真命题的个数是
A.1 B.2
C.3 D.4
【答案】C
【解析】作出不等式组所表示的平面区域如图中阴影部分所示,对于p1,当取图中内(包括边界)的点时,2y≤x,由可得A(4,4),由可得C(4,2),故S△OAB=×4×4=8,S△OBC=×4×2=4,
3.含有一个量词的命题的否定
→→→
【例4】写出下列命题的否定,并判断其真假:
(1):;
(2)至少有一个实数,使得.
【解析】(1)否定是,因为,所以否定后的命题是一个真命题.
(2)否定是,是假命题,如:时,.
【名师点睛】(1)一般地,写含有一个量词的命题的否定,首先要明确这个命题是全称命题还是特称命题,并找到量词及相应结论,然后把命题中的全称量词改成存在量词,存在量词改成全称量词,同时否定结论.
(2)对于省略量词的命题,应先挖掘命题中隐含的量词,改写成含量词的完整形式,再依据规则来写出命题的否定.
4.利用全称命题与特称命题求参数的取值范围
含有变量的语句为命题,即对变量有了限制条件,而它的真假要根据限制条件中变量的取值来确定.因此可将此类题目看成全称命题来解决,即不等式的解集内的任意一个的取值都使得为真命题.
应用全称命题与特称命题求参数范围的常见题型:
(1)全称命题的常见题型是“恒成立”问题,全称命题为真时,意味着命题对应的集合中的每一个元素都具有某种性质,所以可以代入,也可以根据函数等数学知识来解决.
(2)特称命题的常见题型是以适合某种条件的结论“存在”“不存在”“是否存在”等语句表达.解答这类问题,一般要先对结论作出肯定存在的假设,然后从肯定的假设出发,结合已知条件进行推理证明,若推出合理的结论,则存在性随之解决;若导致矛盾,则否定了假设.
【例5】若“?x∈[0,],tan x≤m”是真命题,则实数m的最小值为 .?
【答案】1
【例6】已知命题”;命题?“=”,若命题“”是真命题,求实数的取值范围.
【解析】因为“且”是真命题,所以为真命题,也为真命题.
命题?“对任意的”,
当时,,
对任意成立,
所以.
命题?“存在”,
根据二次函数性质得,即,
解得或.
综上,的取值范围为或.
5.对含有一个量词的命题否定不完全
【例7】已知命题:存在一个实数,使得,写出.
【错解一】:存在一个实数,使得.
【错解二】:对任意的实数x,都有.
【错因分析】该命题是特称命题,其否定应是全称命题,但错解一得到的仍是特称命题,显然只对结论进行了否定,而没有对存在量词进行否定.错解二只对存在量词进行了否定,而没有对结论进行否定.
【正解】:对任意的实数x,都有.
【名师点睛】对含有量词的命题进行否定时,(1)牢记全称命题的否定是特称命题,特称命题的否定是全称命题,注意不能只否定结论,而忘记了对量词的否定;也不能只否定量词,而忘记了对结论的否定.(2)牢记命题的否定与原命题的真假性相反,可以以此检验命题的否定是否正确.
基础训练
1.下列命题为特称命题的是
A.任意一个三角形的内角和为 B.棱锥仅有一个底面
C.偶函数的图象关于轴垂直 D.存在大于1的实数,使
2.
A. B.
C. D.
3.下列命题中是全称命题并且是真命题的是
A.每个二次函数的图象与x轴都有两个不同的交点
B.对任意非正数c,若a≤b+c,则a≤b
C.存在一个菱形不是平行四边形
D.存在一个实数x使不等式x2-3x+7<0成立
4.已知命题.若为假命题,则的取值范围为
A. B.
C. D.
5.给出下列四个命题:
①对任意的x∈R,x2>0;
②存在x∈R,使得x2≤x成立;
③对于集合M,N,若x∈M∩N,则x∈M且x∈N;
④存在α,β∈R,使tan(α+β)=tan?α+tan?β.
其中真命题的个数是
A.0 B.1
C.2 D.3
6.全称命题“对任意实数x,都有x2-2x+1=0成立”含有全称量词 .?
7.命题“能被2整除的数,末位数字是0”的否定是 .?
8.写出下列命题的否定,并判断命题的真假:
(1);
(2)
9.若命题“对任意实数”是真命题,求实数m的取值范围.
能力提升
10.下列说法正确的是
A.命题“若,则”的否命题为:“若,则”
B.命题“若,则”的逆否命题为假命题
C.命题“存在,使得”的否定是:“对任意,均有”
D.中,是的充要条件
11.下列命题中是假命题的是
A.使
B.,函数都不是偶函数
C.使是幂函数,且在上单调递减
D.,函数有零点
12.命题,命题,真命题的是
A. B.
C. D.
13.已知命题“”,“,成立”.如果“”为真,“”为假,求实数的取值范围.
真题练习
14.(2019年高考浙江模拟) 命题“,使得”的否定形式是
A.,使得
B.,使得
C.,使得
D.,使得
15.(2019年四川模拟)设命题,则 为
A.?n∈N,n2>2n B.?n∈N,n2≤2n
C.?n∈N,n2≤2n D.?n∈N,n2=2n
16.(2019年高考重庆模拟)命题“对任意,都有”的否定为
A.对任意,都有 B.不存在,使得
C.存在,使得 D.存在,使得
17.(2019年青岛模拟)设,集合是奇数集,集合是偶数集.若命题,,则
A., B.,
C., D.,
18.(2019年辽宁模拟)下列命题中,真命题是
A.
B.
C.的充要条件是
D.是的充分条件
19.(2019年高考山东模拟)若“”是真命题,则实数m的最小值为__________________.
20.(2019年高考湖南模拟)设函数
(1)记集合,则所对应的的零点的取值集合为__________________.
(2)若__________________.(写出所有正确结论的序号)
①
②
③若
参考答案
1
2
3
4
5
10
11
12
14
15
16
17
18
D
D
B
D
D
D
B
C
D
C
D
D
D
1.【答案】D
2.【答案】D
【解析】因为是特称命题,所以命题p的否定是全称命题,.
3.【答案】B
【解析】对于A,是全称命题,但是假命题,故A错误;
对于B,是全称命题,是真命题,故B正确;
对于C,是特称命题,但是假命题,故C错误;
对于D,是特称命题,但是假命题,故D错误.
故选B.
4.【答案】D
【解析】为假命题,等价于方程无正实根,即,得,
则的取值范围为,故选D.
5.【答案】D
【解析】对于①,存在x=0,使x2=0,故①是假命题;显然②③④是真命题.
6.【答案】任意
【解析】“对任意实数x,都有x2-2x+1=0成立”含有全称量词“任意”.
7.【答案】有些能被2整除的数,末位数字不是0
【解析】原命题省略了全称量词“任何一个”,故其否定为有些能被2整除的数,末位数字不是0.
9.【解析】由题意知,不等式恒成立,
即不等式恒成立.
(1)当时,不等式可化为,显然不恒成立,不合题意.
(2)当时,要使不等式恒成立,则解得.
综上可知,所求实数的取值范围是.
10.【答案】D
【解析】A.否命题是将原命题的条件与结论都否定,因此A错误;B.命题“若,则”显然为真命题,由于互为逆否命题的两个命题同真同假,故逆否命题为真命题,因此B错误;C.由特称命题否定的定义可得,C错误,故答案为D.
11.【答案】B
【解析】对于选项A,如当时,所以选项A的命题为真命题;对于选项B,当时,函数
是偶函数,因此选项B中的命题为假命题;对于选项C,如当时,,在上单调递减,所以选项C中的命题为真命题,对于选项D中,令,则,所以当时,结合函数的图象易知有零点,所以选项D的命题为真命题.
12.【答案】C
13.【解析】若是真命题,则关于的方程有实数解,
由于,∴.
若为真,则成立,即成立.
设,则在上是增函数,∴的最大值为,∴,
∴为真时,.
∵“”为真,“”为假,∴与—真一假.
当真假时,;
当假真时,.
综上所述,实数的取值范围是.
14.【答案】D
【解析】的否定是,的否定是,的否定是.故选D.
【方法点睛】全称命题的否定是特称命题,特称命题的否定是全称命题.对含有存在(全称)量词的命题进行否定需要两步操作:①将存在(全称)量词改成全称(存在)量词;②将结论加以否定.
15.【答案】C
【解析】根据定义可知,?p为,故选C .
16.【答案】D
【解析】根据定义可知命题的否定为存在,使得.故选D.
17.【答案】D
【名师点睛】本题考查命题的含义以及全称命题的否定,注意:“任意”的否定是“存在”,“属于”的否定是“不属于”.
18.【答案】D
【解析】因为,所以排除A;取则,故排除B;,取,则不能推出,故排除C.故选D.
19.【答案】1
【解析】若“”是真命题,则,其中,
∵函数,的最大值为1,∴,即的最小值为1.
20.【答案】(1);(2)①②③
【解析】(1)由题设知,,则,即.又从而,,∴,解得.故所求取值集合为;
