人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题3.1.3 空间向量的数量积运算
文档属性
| 名称 | 人教版高中数学选修2-1知识讲解,巩固练习(教学资料,补习资料):专题3.1.3 空间向量的数量积运算 |  | |
| 格式 | zip | ||
| 文件大小 | 827.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-27 17:15:14 | ||
图片预览




文档简介
知识
1.空间两向量的夹角
如图1,已知两个非零向量,,在空间任取一点,作,,则≤≤叫做向量,的夹角,记作.
由上述概念可知0≤≤,因此,两个向量的夹角是唯一确定的,且.
如图2,当时,向量,_______;
如图3,当时,向量,_______,记作;
如图4,当时,向量,_______.
因此,当时,或.
对于空间任意两个向量,,都有.
图1 图2 图3 图4
2.空间向量的数量积
已知两个非零向量,,则叫做,的数量积,记作,即_______.
类比平面向量,我们可得的几何意义:数量积等于的长度与在的方向上的投影的乘积.
由此可知,零向量与任何向量的数量积为_______.
3.空间向量数量积的性质
(1)若是非零向量,是任意单位向量,则.
(2)若,是非零向量,则.
(3).
(4)若为与的夹角,则_______.
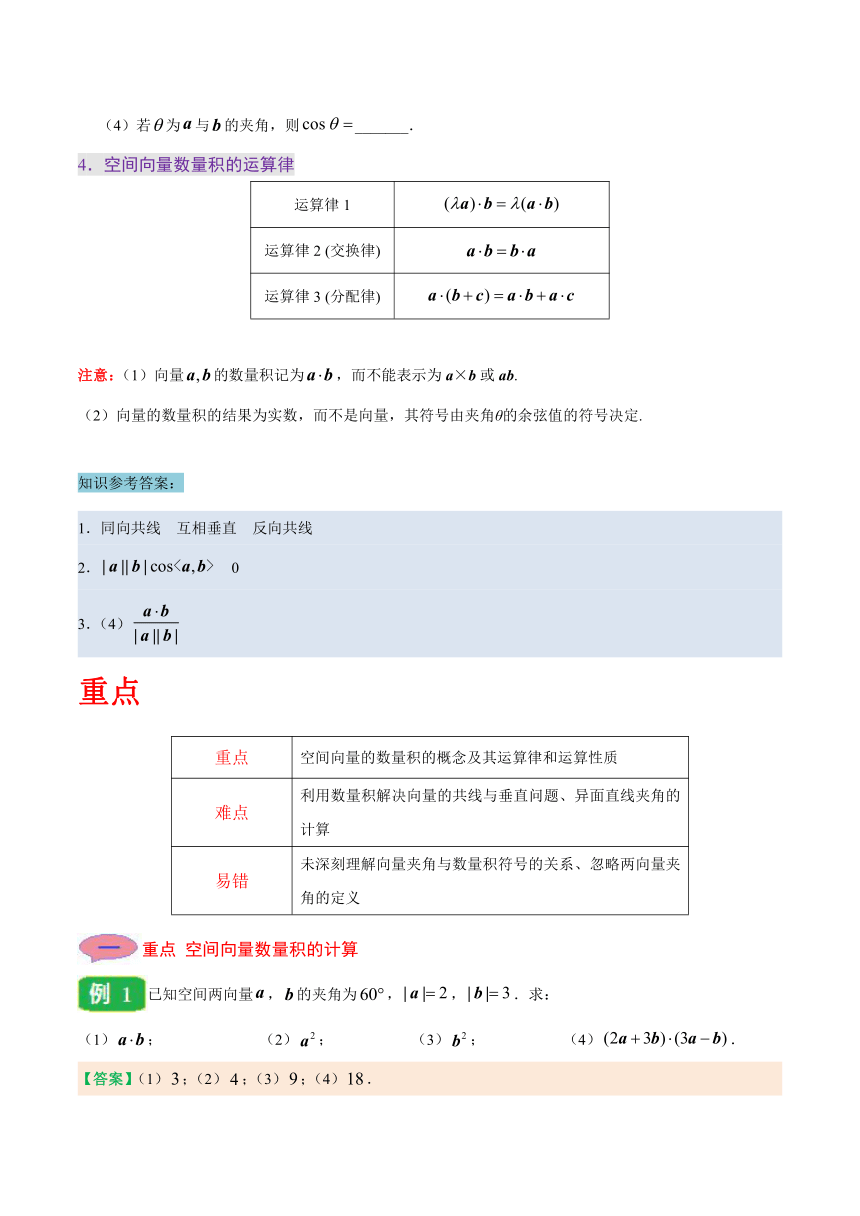
4.空间向量数量积的运算律
运算律1
运算律2 (交换律)
运算律3 (分配律)
注意:(1)向量的数量积记为,而不能表示为a×b或ab.
(2)向量的数量积的结果为实数,而不是向量,其符号由夹角θ的余弦值的符号决定.
知识参考答案:
1.同向共线 互相垂直 反向共线
2. 0
3.(4)
重点
重点
空间向量的数量积的概念及其运算律和运算性质
难点
利用数量积解决向量的共线与垂直问题、异面直线夹角的计算
易错
未深刻理解向量夹角与数量积符号的关系、忽略两向量夹角的定义
重点 空间向量数量积的计算
已知空间两向量,的夹角为,,.求:
(1); (2); (3); (4).
【答案】(1);(2);(3);(4).
【名师点睛】根据数量积的定义求解即可,应注意准确确定向量的夹角.
如图,已知空间四边形ABCD的每条边和对角线长都等于a,点E、F、G分别是AB、AD、DC的中点.求下列向量的数量积:
(1); (2);
(3); (4).
【解析】(1)在空间四边形ABCD中,,且,
∴;
(2),,,
∴;
(3),,
又∵,,
∴;
【名师点睛】在几何体中求空间向量的数量积时,
①充分利用向量所在的图形,将各向量分解成已知模和夹角的向量的组合形式;
②利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
③利用数量积的定义求解即可.注意挖掘几何体中的垂直关系或者特殊角.
难点 利用数量积证明垂直问题
如图,在正方体中,为与的交点,为的中点.求证:平面.
【解析】设,,,则,,.
而,
,
.
∴
.
∴,∴.
同理可证,∴.
又且平面,
∴平面.
【名师点睛】(1)要证两直线垂直,由数量积的性质可知,可构造与两直线分别平行的向量,只要证明这两个向量的数量积为0即可;
(2)用向量法证明线面垂直,离不开线面垂直的判定定理,需将线面垂直转化为线线垂直,然后利用向量法证明线线垂直即可.
难点 利用数量积求异面直线的夹角
求几何体中异面直线的夹角,可将问题转化为求向量的夹角,步骤如下:
(1)依据夹角公式,求出的余弦值;
(2)若求出,则是异面直线所成的角;
若求出,则是异面直线所成的角,为;
若求出,则是异面直线所成角的补角.
在棱长为的正方体中,求异面直线与所成的角.
【解析】,,
,
,,,
,,,
又,,
,,
∴,
,
即异面直线与所成的角为.
【名师点睛】解决本题的关键是在两异面直线上构造向量,求出向量的夹角,在求解过程中易忽略向量的夹角与两直线所成的角的区别.
重点 利用数量积求线段的长或两点间的距离
利用空间向量求线段的长度或两点间的距离,步骤如下:
(1)结合图形将所求线段用向量表示;
(2)用已知夹角和模的向量表示该向量;
(3)利用,通过计算求出,即可得,即得所求线段的长度或两点间的距离.
如图所示,一块矿石晶体的形状为四棱柱ABCD-A1B1C1D1,底面ABCD是正方形,CC1=3,CD=2,且∠C1CB=∠C1CD=60°.
(1)设=a,=b,=c,试用a,b,c表示;
(2)已知O为四棱柱ABCD-A1B1C1D1的中心,求CO的长.
【解析】(1)由=a,=b,=c,得=a+b+c,
所以=-a-b-c.
(2)O为四棱柱ABCD-A1B1C1D1的中心,即O为线段A1C的中点.
由已知条件得|a|=|b|=2,|c|=3,a·b=0,.
由(1)得=a+b+c,
则||2==(a+b+c)2=a2+b2+c2+2a·b+2b·c+2a·c
=22+22+32+0+2×2×3×cos 60°+2×2×3×cos 60°=29.
所以A1C的长为,
所以CO的长为.
易错 未深刻理解向量夹角与数量积符号的关系导致错误
“”是“为钝角”的______________条件.
【错解】易知为钝角,
所以“”是“为钝角”的充要条件.
【错因分析】错解中忽略了两个向量共线且反向的情况从而导致错误.
【正解】易知为钝角或平角,
所以“”是“为钝角”的必要不充分条件.
【名师点睛】,即夹角为钝角或平角,不能忽略与平行且反向的情形;
,即夹角为直角;
,即夹角为零角或锐角,不能忽略与平行且同向的情形.
易错 忽略向量夹角的定义导致错误
如图所示,在空间四边形中,,,,,分别为,的中点,则______________.
【错解】由题易知,,
所以.
【错因分析】错解中没有正确理解两向量的夹角,误认为是与的夹角.
【正解】由题易知,,
所以.
【名师点睛】向量的夹角定义中,必须把两向量移至共起点,如下图所示,是与的夹角,而与的夹角为的补角.
基础训练
1.已知,,,则
A. B.
C. D.
2.设是棱长为的正方体,和相交于点,则有
A. B.
C. D.
3.若非零向量,满足,,则与的夹角为
A. B.
C. D.
4.已知四边形为矩形(邻边不相等),平面,连接、、、、,则下列各组向量中,数量积不为零的是
A.与 B.与
C.与 D.与
5.在空间四边形ABCD中,·+·+·=
A.0 B.
C.1 D.无法确定
6.一个结晶体的形状是平行六面体,以顶点为端点的三条棱长均是1,且它们彼此的夹角都是,则对角线的长度是
A. B.2
C. D.
7.已知是异面直线,且则与所成的角是
A. B.
C. D.
8.在空间四边形中,,,则等于
A. B.
C. D.
9.在棱长为的正方体中,___________.
10.已知空间向量a,b满足,,a与b的夹角为150°,则___________.
11.已知,,,则___________.
12.如图所示,在棱长为1的正方体ABCD-A1B1C1D1中,向量在向量上的投影是___________.?
13.如图,在空间四边形中,,,求异面直线与的夹角.
14.如图,在正方体ABCD-A1B1C1D1中,P是DD1的中点,O是底面ABCD的中心.求证:B1O⊥平面PAC.
能力提升
15.若a,b均为非零向量,则a·b=|a||b|是a与b共线的
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
16.设,,,是空间不共面的四个点,且满足,,,则的形状是
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰直角三角形
17.已知,且与垂直,则与的夹角为
A. B.
C. D.
18.在平行四边形中,,,,若、分别是边、上的点,且满足,则的取值范围是
A. B.
C. D.
19.如图,正四面体中,是的中点,那么
A. B.
C. D.与不能比较大小
20.设,,与垂直,,,则_________________.
21.如图,平面,且△是的等腰直角三角形,四边形、四边形都是正方形,若,求异面直线与所成的角.
22.如图,在平行四边形中,,,,沿着它的对角线将折起,使与成角,求此时,之间的距离.
23.如图,已知平行六面体ABCD-A1B1C1D1的底面ABCD是菱形,且∠C1CB=∠C1CD=∠BCD=60°.当的值等于多少时,能使A1C⊥平面C1BD?
真题练习
24.(2019上海模拟)如图,四个棱长为1的正方体排成一个正四棱柱,AB是一条侧棱,是上底面上其余的八个点,则的不同值的个数为
A.1 B.2
C.4 D.8
25.(2019天津模拟)如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=
AB=2,E为棱AA1的中点.证明B1C1⊥CE.
参考答案
1.【答案】C
2.【答案】C
【解析】由.故选C.
3.【答案】C
【解析】由,可得,则,故与的夹角为.故选C.
4.【答案】A
【解析】由图分析可知(图略),选项B、C、D中两向量的夹角均为,∴数量积都为,故选A.
5.【答案】A
【解析】·+·+··(-)+(-)·+(-)··-·+·
-·+·-·=0,故选A.
6.【答案】D
【解析】,故选D.
7.【答案】C
8.【答案】D
【解析】
,∴
9.【答案】
【解析】由题意知,所以,又,所以.故填.
10.【答案】
【解析】
11.【答案】
【解析】由,得,所以,
所以即所以.
12.【答案】
【解析】向量在上的投影为||cos<,>=||cos<,>=1×cos 45°=.
14.【解析】连结DB,令,,,且|a|=|b|=|c|=1,
则,,
.
,
∴,即AC⊥OB1.
又,
∴.
∴,即.
∵AP∩AC=A,
∴OB1⊥平面ACP.
15.【答案】B
【解析】∵a·b=|a||b|cos〈a,b〉,a·b=|a||b|,∴cos〈a,b〉=1,∴〈a,b〉=0,∴a与b共线.反之,当a与b共线时,也可能a·b=-|a|·|b|,故a·b=|a||b|是a与b共线的充分不必要条件,故选B.
16.【答案】A
17.【答案】D
【解析】∵与垂直,∴,
∴
∴
18.【答案】D
【解析】设.
则
,选D.
19.【答案】C
【解析】∵,
,
∴.
20.【答案】
21.【解析】∵,,
∴.
∵,,,
∴,,,.
∴.
又,
∴,∴,
∴异面直线与所成的角为.
22.【解析】因为,所以,.
因为与成角,所以或.
因为,
所以,
所以.
当时,,即;
当时,,即.
综上,可知,之间的距离为或.
【名师点睛】求解本题应注意:与成角,有,两种情况.
24.【答案】A
【解析】由题图可知,与上底面垂直,因此,.
25.【解析】因为·=(++)·(++)=(++)·+(++)·
+(++)·,
又(++)·=2+0+(-1)=1,
(++)·=0+(-1)+0=-1,
(++)·=0,
所以·=1+(-1)+0=0,因此B1C1⊥CE.
