山东省肥城市边院镇初级中学2019—2020学年上学期八年级数学第一次月考试卷(9月)(pdf版含答案)
文档属性
| 名称 | 山东省肥城市边院镇初级中学2019—2020学年上学期八年级数学第一次月考试卷(9月)(pdf版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 690.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-23 21:30:20 | ||
图片预览


文档简介
数学试卷 第 1 页(共 12 页) 数学试卷 第
2 页(共 12 页)
2019-2020 学年度上学期第一次月考
八年级数学试卷
2019.9
一、选择题(每小题 3 分:共 30 分)
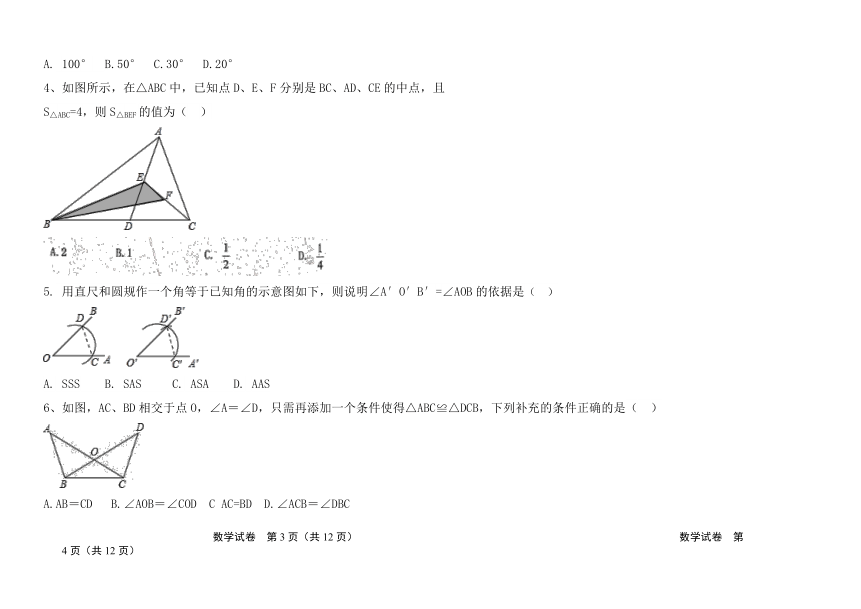
1. 下列图案是我国几家银行的标志,其中既是轴对称图形,又是中心对称图形的有( )
2.在△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2= ( )
A.360度 B.250度 C.180度 D.140
3.如图,△ABC与△A'B'C'关于直线 1对称,则∠B的度数为( )
密
封
线
内
不
要
答
题
学
校
班
级
姓
名
学
号
数学试卷 第 3 页(共 12 页) 数学试卷 第
4 页(共 12 页)
A. 100° B.50° C.30° D.20°
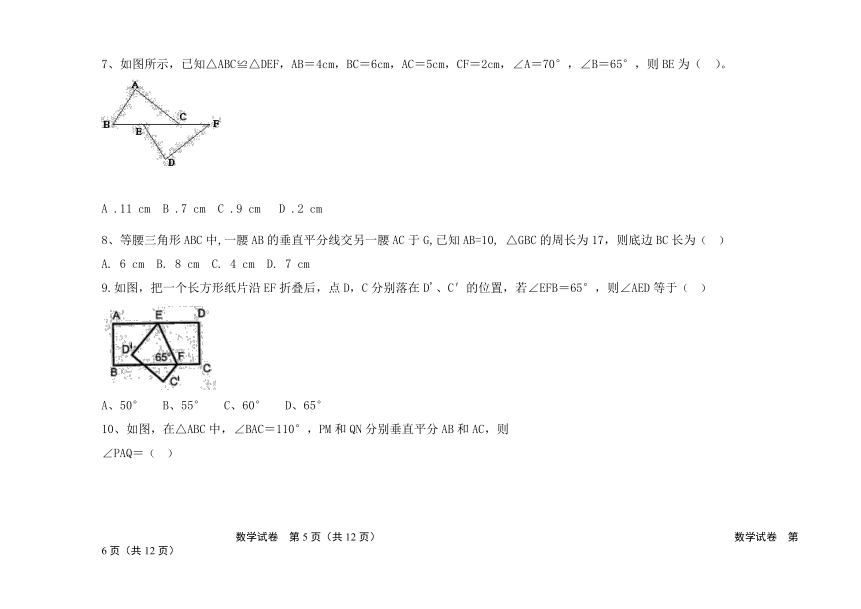
4、如图所示,在△ABC中,已知点 D、E、F分别是 BC、AD、CE的中点,且
S△ABC=4,则 S△BEF的值为( )
5. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
A. SSS B. SAS C. ASA D. AAS
6、如图,AC、BD相交于点 O,∠A=∠D,只需再添加一个条件使得△ABC≌△DCB,下列补充的条件正确的是( )
A.AB=CD B.∠AOB=∠COD C AC=BD D.∠ACB=∠DBC
数学试卷 第 5 页(共 12 页) 数学试卷 第
6 页(共 12 页)
7、如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则 BE为( )。
A .11 cm B .7 cm C .9 cm D .2 cm
8、等腰三角形 ABC中,一腰 AB的垂直平分线交另一腰 AC于 G,已知 AB=10, △GBC的周长为 17,则底边 BC长为( )
A. 6 cm B. 8 cm C. 4 cm D. 7 cm
9.如图,把一个长方形纸片沿 EF折叠后,点 D,C分别落在 D'、C'的位置,若∠EFB=65°,则∠AED等于( )
A、50° B、55° C、60° D、65°
10、如图,在△ABC中,∠BAC=110°,PM和 QN分别垂直平分 AB和 AC,则
∠PAQ=( )
数学试卷 第 7 页(共 12 页) 数学试卷 第
8 页(共 12 页)
A.30 B.40 C.50 D.60
11、如下图.有 A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,
则超市应建在( )
A.在 AC、BC两边高线的交点处
B.在 AC、BC两边中线的交点处
C.在 AC、BC两边垂直平分线的交点处
D.在∠A、∠B两内角平分线的交点处
数学试卷 第 9 页(共 12 页) 数学试卷 第
10 页(共 12 页)
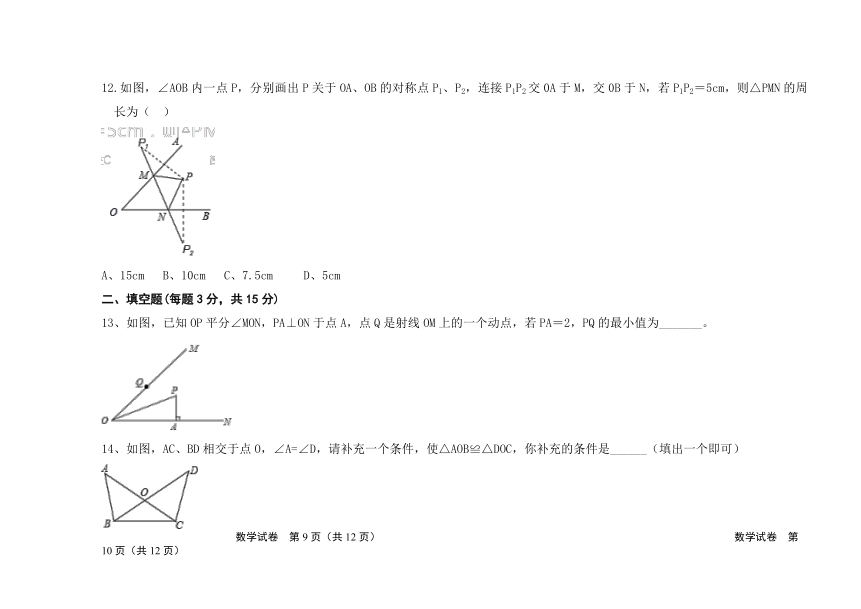
12.如图,∠AOB内一点 P,分别画出 P关于 OA、OB的对称点 P1、P2,连接 P1P2交 0A于 M,交 0B于 N,若 P1P2=5cm,则△PMN的周
长为( )
A、15cm B、10cm C、7.5cm D、5cm
二、填空题(每题 3 分,共 15 分)
13、如图,已知 OP平分∠MON,PA⊥ON于点 A,点 Q是射线 OM上的一个动点,若 PA=2,PQ的最小值为_______。
14、如图,AC、BD相交于点 O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是______(填出一个即可)
数学试卷 第 11 页(共 12 页) 数学试卷
第 12 页(共 12 页)
15.等腰三角形的两边长分别为 9 cm、4cm,则三角形周长为__________。
16. 如图,已知△ABC是等边三角形,点 B、C、D、E在同一直线上,且 CG=CD,DF=DE,则∠E=________度。
17、如图所示,Rt△ABC中、∠ACB=900,∠A=500,将其折叠,使 A落在边 CB
上的点 E处,折痕为 CD,则∠BDE=________。
数学试卷 第 13 页(共 12 页) 数学试卷 第
14 页(共 12 页)
18.如图,C为线段 AE上一动点(不与点 A,E重合),在 AE同侧分别作正三角形
ABC和正三角形 CDE、AD与 BE交于点 O,AD与 BC交于点 P,BE与 CD交于点 Q,
连接 PQ、OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;
⑤∠AOB=600。恒成立的结论有__________(把你认为正确的序号都填上)。
三、解答题(按要求答题,写出必要的步骤和过程)
19、如图,已知 AB=AD,AC=AE,∠1=∠2。试说明 BC=DE。
数学试卷 第 15 页(共 12 页) 数学试卷
第 16 页(共 12 页)
20、用直尺和圆规按下列要求作图:(不写作法,保留作图痕迹)
(1)作∠ABC的角平分线
(2)过点 P作 L的垂线
数学试卷 第 17 页(共 12 页) 数学试卷 第
18 页(共 12 页)
21、如图,AB∥DE,AB=DE,BE=CF,求证:AC∥DF
数学试卷 第 19 页(共 12 页) 数学试卷
第 20 页(共 12 页)
22.(8分)如图,∠ABC=90°,AB=BC,D为 AC上一点,分别过 A.C作 BD的垂线,垂足分别为 E、F,求证: EF=CF-AE
数学试卷 第 21 页(共 12 页) 数学试卷 第
22 页(共 12 页)
23、如图,在△ABC中,∠ABC和∠ACB的平分线交于点 O,过点 O作 EF∥BC,交 AB于 E、交 AC于 F.
(1)请写出图中的一个等腰三角形,并说明理由;
(2)若 AB=8,AC=6,求△AEF的周长
数学试卷 第 23 页(共 12 页) 数学试卷
第 24 页(共 12 页)
24. (1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线 m经过点 A,BD⊥直线 m,CE⊥直线 m,垂足分别为点 D、E,证
明:△ABD≌△CAE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线 m上,并且有∠BDA=∠AEC=∠BAC=α,其中α
为任意锐角或钝角.试说明 DE=BD+CE
数学试卷 第 25 页(共 12 页) 数学试卷 第
26 页(共 12 页)
数学试卷 第 27 页(共 12 页) 数学试卷
第 28 页(共 12 页)
参考答案
一、选择题(每小题 3分:共 30分)
1-5BBABA 6-10DDDDB 11-12CD
二、填空题(每题 3分,共 15分)
13.2
14.AB=CD
15.22 cm
16.15度
17. 100
18. ①②③⑤
三、解答题(按要求答题,写出必要的步骤和过程)
19. 解:在ΔABC 和ΔADE 中:∠BAC=∠1+∠EAC,∠EAD=∠2+∠EAC
又∵∠1=∠2
∴∠BAC=∠EAD
在△ABC与△ADE中
AB=AD
∠BAC=∠EAD
AC=AE
∴ΔABC≌ΔADE (SAS)
∴BC=DE
数学试卷 第 29 页(共 12 页) 数学试卷 第
30 页(共 12 页)
20. (1)(2)如图所示:
21. 证明:∵AB∥CD,
∴∠ABC=∠DEF,
又∵BE=CF,
∴BE+EC=CF+EC,
即:BC=EF,
在△ABC和△DEF中
AB=DE
∠ABC=∠DEF
BC=EF
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴AC∥DF.
22. 证明:
∵AE⊥BD,CF⊥BD
数学试卷 第 31 页(共 12 页) 数学试卷
第 32 页(共 12 页)
∴∠AEB=∠CFB=90
∴∠ABE+∠BAE=90
∵∠ABC=90
∴∠ABE+∠CBF=90
∴∠BAE=∠CBF
∵AB=BC
∴△ABE≌△CBF (AAS)
∴BE=CF,BF=AE
∵EF=BE-BF
∴EF=CF-AE
23. (1)图中的等腰三角形有△BEO(或△CFO).
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
(2)同(1)可证△OFC也为等腰三角形,
∴OE=BE,OF=FC,
∴△AEF的周长=AE+AF+OE+OF=AE+AF+BE+FC=AB+AC=6+8=14.
数学试卷 第 33 页(共 12 页) 数学试卷 第
34 页(共 12 页)
24. (1)证明:
∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中
∠BDA=∠CEA
∠ABD=∠CAE
AB=AC
∴△ABD≌△CAE(AAS),
(2)证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中
∠BDA=∠CEA
∠ABD=∠CAE
AB=AC
∴△ABD≌△CAE(AAS),
数学试卷 第 35 页(共 12 页) 数学试卷
第 36 页(共 12 页)
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
2 页(共 12 页)
2019-2020 学年度上学期第一次月考
八年级数学试卷
2019.9
一、选择题(每小题 3 分:共 30 分)
1. 下列图案是我国几家银行的标志,其中既是轴对称图形,又是中心对称图形的有( )
2.在△ABC中,∠C=70°,若沿图中虚线截去∠C,则∠1+∠2= ( )
A.360度 B.250度 C.180度 D.140
3.如图,△ABC与△A'B'C'关于直线 1对称,则∠B的度数为( )
密
封
线
内
不
要
答
题
学
校
班
级
姓
名
学
号
数学试卷 第 3 页(共 12 页) 数学试卷 第
4 页(共 12 页)
A. 100° B.50° C.30° D.20°
4、如图所示,在△ABC中,已知点 D、E、F分别是 BC、AD、CE的中点,且
S△ABC=4,则 S△BEF的值为( )
5. 用直尺和圆规作一个角等于已知角的示意图如下,则说明∠A′O′B′=∠AOB的依据是( )
A. SSS B. SAS C. ASA D. AAS
6、如图,AC、BD相交于点 O,∠A=∠D,只需再添加一个条件使得△ABC≌△DCB,下列补充的条件正确的是( )
A.AB=CD B.∠AOB=∠COD C AC=BD D.∠ACB=∠DBC
数学试卷 第 5 页(共 12 页) 数学试卷 第
6 页(共 12 页)
7、如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,CF=2cm,∠A=70°,∠B=65°,则 BE为( )。
A .11 cm B .7 cm C .9 cm D .2 cm
8、等腰三角形 ABC中,一腰 AB的垂直平分线交另一腰 AC于 G,已知 AB=10, △GBC的周长为 17,则底边 BC长为( )
A. 6 cm B. 8 cm C. 4 cm D. 7 cm
9.如图,把一个长方形纸片沿 EF折叠后,点 D,C分别落在 D'、C'的位置,若∠EFB=65°,则∠AED等于( )
A、50° B、55° C、60° D、65°
10、如图,在△ABC中,∠BAC=110°,PM和 QN分别垂直平分 AB和 AC,则
∠PAQ=( )
数学试卷 第 7 页(共 12 页) 数学试卷 第
8 页(共 12 页)
A.30 B.40 C.50 D.60
11、如下图.有 A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,
则超市应建在( )
A.在 AC、BC两边高线的交点处
B.在 AC、BC两边中线的交点处
C.在 AC、BC两边垂直平分线的交点处
D.在∠A、∠B两内角平分线的交点处
数学试卷 第 9 页(共 12 页) 数学试卷 第
10 页(共 12 页)
12.如图,∠AOB内一点 P,分别画出 P关于 OA、OB的对称点 P1、P2,连接 P1P2交 0A于 M,交 0B于 N,若 P1P2=5cm,则△PMN的周
长为( )
A、15cm B、10cm C、7.5cm D、5cm
二、填空题(每题 3 分,共 15 分)
13、如图,已知 OP平分∠MON,PA⊥ON于点 A,点 Q是射线 OM上的一个动点,若 PA=2,PQ的最小值为_______。
14、如图,AC、BD相交于点 O,∠A=∠D,请补充一个条件,使△AOB≌△DOC,你补充的条件是______(填出一个即可)
数学试卷 第 11 页(共 12 页) 数学试卷
第 12 页(共 12 页)
15.等腰三角形的两边长分别为 9 cm、4cm,则三角形周长为__________。
16. 如图,已知△ABC是等边三角形,点 B、C、D、E在同一直线上,且 CG=CD,DF=DE,则∠E=________度。
17、如图所示,Rt△ABC中、∠ACB=900,∠A=500,将其折叠,使 A落在边 CB
上的点 E处,折痕为 CD,则∠BDE=________。
数学试卷 第 13 页(共 12 页) 数学试卷 第
14 页(共 12 页)
18.如图,C为线段 AE上一动点(不与点 A,E重合),在 AE同侧分别作正三角形
ABC和正三角形 CDE、AD与 BE交于点 O,AD与 BC交于点 P,BE与 CD交于点 Q,
连接 PQ、OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;
⑤∠AOB=600。恒成立的结论有__________(把你认为正确的序号都填上)。
三、解答题(按要求答题,写出必要的步骤和过程)
19、如图,已知 AB=AD,AC=AE,∠1=∠2。试说明 BC=DE。
数学试卷 第 15 页(共 12 页) 数学试卷
第 16 页(共 12 页)
20、用直尺和圆规按下列要求作图:(不写作法,保留作图痕迹)
(1)作∠ABC的角平分线
(2)过点 P作 L的垂线
数学试卷 第 17 页(共 12 页) 数学试卷 第
18 页(共 12 页)
21、如图,AB∥DE,AB=DE,BE=CF,求证:AC∥DF
数学试卷 第 19 页(共 12 页) 数学试卷
第 20 页(共 12 页)
22.(8分)如图,∠ABC=90°,AB=BC,D为 AC上一点,分别过 A.C作 BD的垂线,垂足分别为 E、F,求证: EF=CF-AE
数学试卷 第 21 页(共 12 页) 数学试卷 第
22 页(共 12 页)
23、如图,在△ABC中,∠ABC和∠ACB的平分线交于点 O,过点 O作 EF∥BC,交 AB于 E、交 AC于 F.
(1)请写出图中的一个等腰三角形,并说明理由;
(2)若 AB=8,AC=6,求△AEF的周长
数学试卷 第 23 页(共 12 页) 数学试卷
第 24 页(共 12 页)
24. (1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线 m经过点 A,BD⊥直线 m,CE⊥直线 m,垂足分别为点 D、E,证
明:△ABD≌△CAE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线 m上,并且有∠BDA=∠AEC=∠BAC=α,其中α
为任意锐角或钝角.试说明 DE=BD+CE
数学试卷 第 25 页(共 12 页) 数学试卷 第
26 页(共 12 页)
数学试卷 第 27 页(共 12 页) 数学试卷
第 28 页(共 12 页)
参考答案
一、选择题(每小题 3分:共 30分)
1-5BBABA 6-10DDDDB 11-12CD
二、填空题(每题 3分,共 15分)
13.2
14.AB=CD
15.22 cm
16.15度
17. 100
18. ①②③⑤
三、解答题(按要求答题,写出必要的步骤和过程)
19. 解:在ΔABC 和ΔADE 中:∠BAC=∠1+∠EAC,∠EAD=∠2+∠EAC
又∵∠1=∠2
∴∠BAC=∠EAD
在△ABC与△ADE中
AB=AD
∠BAC=∠EAD
AC=AE
∴ΔABC≌ΔADE (SAS)
∴BC=DE
数学试卷 第 29 页(共 12 页) 数学试卷 第
30 页(共 12 页)
20. (1)(2)如图所示:
21. 证明:∵AB∥CD,
∴∠ABC=∠DEF,
又∵BE=CF,
∴BE+EC=CF+EC,
即:BC=EF,
在△ABC和△DEF中
AB=DE
∠ABC=∠DEF
BC=EF
∴△ABC≌△DEF(SAS),
∴∠ACB=∠DFE,
∴AC∥DF.
22. 证明:
∵AE⊥BD,CF⊥BD
数学试卷 第 31 页(共 12 页) 数学试卷
第 32 页(共 12 页)
∴∠AEB=∠CFB=90
∴∠ABE+∠BAE=90
∵∠ABC=90
∴∠ABE+∠CBF=90
∴∠BAE=∠CBF
∵AB=BC
∴△ABE≌△CBF (AAS)
∴BE=CF,BF=AE
∵EF=BE-BF
∴EF=CF-AE
23. (1)图中的等腰三角形有△BEO(或△CFO).
∵EF∥BC,
∴∠EOB=∠OBC.
∵∠EBO=∠OBC,
∴∠EOB=∠EBO,
∴△BEO是等腰三角形;
(2)同(1)可证△OFC也为等腰三角形,
∴OE=BE,OF=FC,
∴△AEF的周长=AE+AF+OE+OF=AE+AF+BE+FC=AB+AC=6+8=14.
数学试卷 第 33 页(共 12 页) 数学试卷 第
34 页(共 12 页)
24. (1)证明:
∵BD⊥DE,CE⊥DE,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=∠BAD+∠ABD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中
∠BDA=∠CEA
∠ABD=∠CAE
AB=AC
∴△ABD≌△CAE(AAS),
(2)证明如下:
∵∠BDA=∠AEC=∠BAC=a,
∴∠BAD+∠CAE=180°-α,且∠DBA+∠BAD=180°-α,
∴∠DBA=∠CAE,
在△ABD和△CAE中
∠BDA=∠CEA
∠ABD=∠CAE
AB=AC
∴△ABD≌△CAE(AAS),
数学试卷 第 35 页(共 12 页) 数学试卷
第 36 页(共 12 页)
∴BD=AE,CE=DA,
∴DE=AE+DA=BD+CE;
同课章节目录
