江苏省江都区嘶马中学2019-2020学年八年级数学上第3章勾股定理同步提高测试含答案
文档属性
| 名称 | 江苏省江都区嘶马中学2019-2020学年八年级数学上第3章勾股定理同步提高测试含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 121.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-24 15:24:50 | ||
图片预览


文档简介
八年级数学第3章《勾股定理》同步提高测试
一、选择题:
1、下列各组线段能构成直角三角形的一组是( )
A.5 cm,9 cm,12 cm B.7 cm,12 cm,13 cm
C.30 cm,40 cm,50 cm D.3 cm,4 cm,6 cm
2、一直角三角形的斜边长比直角边长大2,另一直角边长为6,则斜边长为( )
A. 4 B. 8 C. 10 D. 12
3、如果△ABC中,∠A:∠B:∠C=1:2:3,那么这个三角形是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形
4、下列叙述中,正确的是( )
A、直角三角形中,两条边的平方和等于第三边的平方
B、如果一个三角形中两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C、△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2+b2=c2,则∠A=90°
D、如果△ABC是直角三角形,且∠C=90°,那么c2=b2-a2
5、如图,在直线 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4=( )
A.2.44 B.4.88 C.3.88 D.3.65
6、一架2.5m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯脚移动的距离是 ( )
A. 1.5m B. 0.9m C. 0.8m D. 0.5m
7、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3,5,2,3,则最大的正方形E的面积是( ).
A.26 B.47 C.36 D.94
8、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
9、如图,矩形纸片ABCD中,已知AD=4,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=.则AB的长为( )
A.2.5 B.4 C.3 D.2.4
10、一根直杆在离地面9米处断折,直杆顶部落在离旗杆底部12米处,直杆折断之前的长度为 ( )
A.15米 B. 18米 C. 21米 D. 24米
11、已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )
A.m2+2mn+n2=0 B.m2﹣2mn+n2=0 C.m2+2mn﹣n2=0 D.m2﹣2mn﹣n2=0
12、如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A.b2+(b﹣a)2 B.b2+a2 C.(b+a)2 D.a2+2ab
二、填空题:
13、已知直角三角形两边,的长满足,则第三边长为______.
14、学校有一块长方形的花圃,有极少数人为了避开拐角而走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了 步路(假设2步为1m),却踩伤了花草。
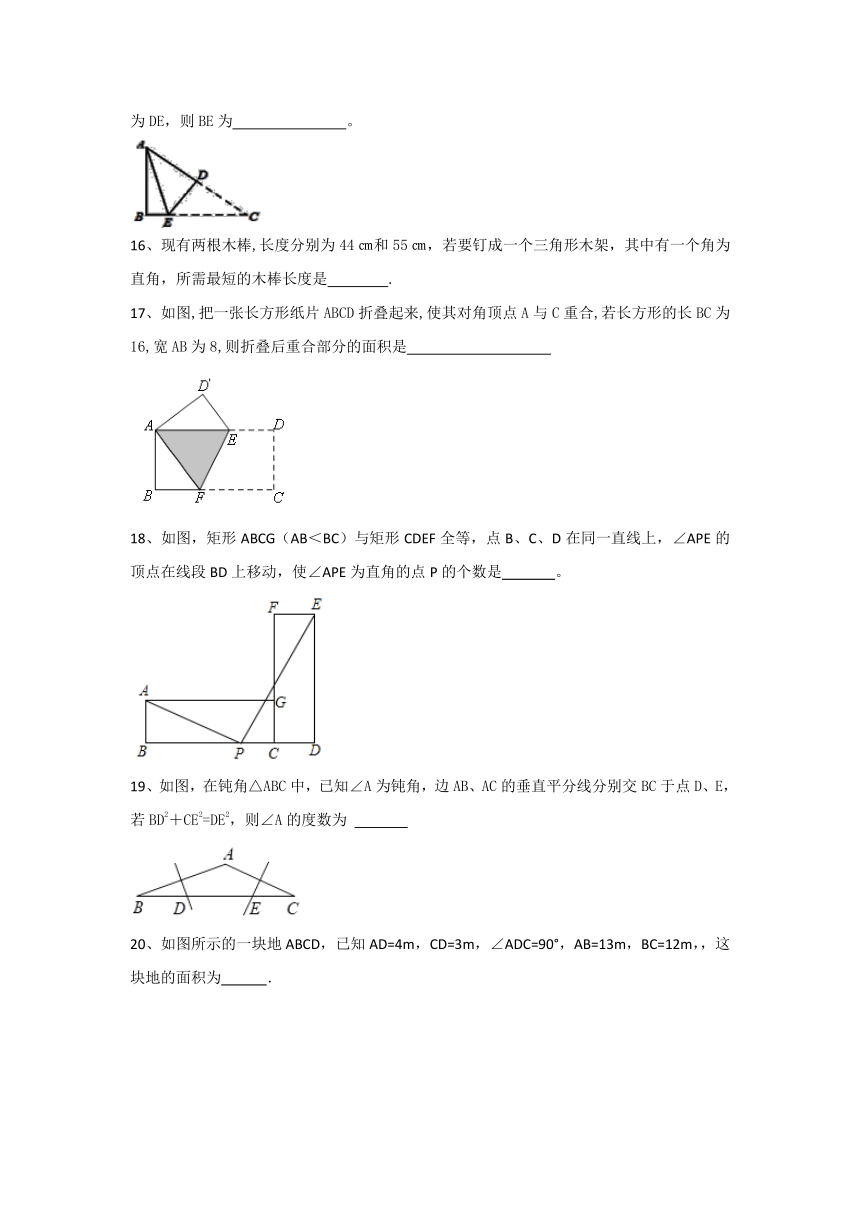
15、如图,在三角形ABC中,∠B=900,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE为 。
16、现有两根木棒,长度分别为44㎝和55㎝,若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是 .
17、如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,若长方形的长BC为16,宽AB为8,则折叠后重合部分的面积是
18、如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B、C、D在同一直线上,∠APE的顶点在线段BD上移动,使∠APE为直角的点P的个数是 。
19、如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为
20、如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,,这块地的面积为 .
21、如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2= .
22、如图所示,P为正方形ABCD内一点,将ABP绕B顺时针旋转到CBE的位置,若BP=,则以PE为边长的正方形的面积为 。
三、解答题:
23、如图,在Rt△ABC中,∠ACB=90°,AC=16,AB=20,CD⊥AB于点D.
(1)求BC的长;(2)求CD的长
24、如图,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。如果M为CD边的中点,且DE=6,求正方形ABCD的面积
25、如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长。
26如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
参考答案:
CC BB AC BD CD CA
13、2√2或√13
14、4
15、7/8
16、33
17、48
18、2
19、135
20、24
21、25
22、2a2
23、25 12
24、256
25、13
26、AO=CQ 直角三角形
一、选择题:
1、下列各组线段能构成直角三角形的一组是( )
A.5 cm,9 cm,12 cm B.7 cm,12 cm,13 cm
C.30 cm,40 cm,50 cm D.3 cm,4 cm,6 cm
2、一直角三角形的斜边长比直角边长大2,另一直角边长为6,则斜边长为( )
A. 4 B. 8 C. 10 D. 12
3、如果△ABC中,∠A:∠B:∠C=1:2:3,那么这个三角形是( )
A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形
4、下列叙述中,正确的是( )
A、直角三角形中,两条边的平方和等于第三边的平方
B、如果一个三角形中两边的平方差等于第三边的平方,那么这个三角形是直角三角形
C、△ABC中,∠A、∠B、∠C的对边分别为a、b、c,若a2+b2=c2,则∠A=90°
D、如果△ABC是直角三角形,且∠C=90°,那么c2=b2-a2
5、如图,在直线 上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1,1.21,1.44,正放置的四个正方形的面积为S1、S2、S3、S4,则S1+S2+S3+S4=( )
A.2.44 B.4.88 C.3.88 D.3.65
6、一架2.5m长的梯子斜靠在一竖直的墙上,这时梯脚距离墙角0.7m,如果梯子的顶端沿墙下滑0.4m,那么梯脚移动的距离是 ( )
A. 1.5m B. 0.9m C. 0.8m D. 0.5m
7、如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的边长分别是3,5,2,3,则最大的正方形E的面积是( ).
A.26 B.47 C.36 D.94
8、若等腰三角形中相等的两边长为10cm,第三边长为16 cm,那么第三边上的高为 ( )
A. 12 cm B. 10 cm C. 8 cm D. 6 cm
9、如图,矩形纸片ABCD中,已知AD=4,折叠纸片使AB边与对角线AC重合,点B落在点F处,折痕为AE,且EF=.则AB的长为( )
A.2.5 B.4 C.3 D.2.4
10、一根直杆在离地面9米处断折,直杆顶部落在离旗杆底部12米处,直杆折断之前的长度为 ( )
A.15米 B. 18米 C. 21米 D. 24米
11、已知直角三角形纸片的两条直角边长分别为m和n(m<n),过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则( )
A.m2+2mn+n2=0 B.m2﹣2mn+n2=0 C.m2+2mn﹣n2=0 D.m2﹣2mn﹣n2=0
12、如图,将一边长为a的正方形(最中间的小正方形)与四块边长为b的正方形(其中b>a)拼接在一起,则四边形ABCD的面积为( )
A.b2+(b﹣a)2 B.b2+a2 C.(b+a)2 D.a2+2ab
二、填空题:
13、已知直角三角形两边,的长满足,则第三边长为______.
14、学校有一块长方形的花圃,有极少数人为了避开拐角而走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了 步路(假设2步为1m),却踩伤了花草。
15、如图,在三角形ABC中,∠B=900,AB=3,AC=5,将△ABC折叠,使点C与点A重合,折痕为DE,则BE为 。
16、现有两根木棒,长度分别为44㎝和55㎝,若要钉成一个三角形木架,其中有一个角为直角,所需最短的木棒长度是 .
17、如图,把一张长方形纸片ABCD折叠起来,使其对角顶点A与C重合,若长方形的长BC为16,宽AB为8,则折叠后重合部分的面积是
18、如图,矩形ABCG(AB<BC)与矩形CDEF全等,点B、C、D在同一直线上,∠APE的顶点在线段BD上移动,使∠APE为直角的点P的个数是 。
19、如图,在钝角△ABC中,已知∠A为钝角,边AB、AC的垂直平分线分别交BC于点D、E,若BD2+CE2=DE2,则∠A的度数为
20、如图所示的一块地ABCD,已知AD=4m,CD=3m,∠ADC=90°,AB=13m,BC=12m,,这块地的面积为 .
21、如图,△ABC中,CE平分∠ACB,CF平分∠ACD,且EF∥BC交AC于M,若EF=5,则CE2+CF2= .
22、如图所示,P为正方形ABCD内一点,将ABP绕B顺时针旋转到CBE的位置,若BP=,则以PE为边长的正方形的面积为 。
三、解答题:
23、如图,在Rt△ABC中,∠ACB=90°,AC=16,AB=20,CD⊥AB于点D.
(1)求BC的长;(2)求CD的长
24、如图,将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G。如果M为CD边的中点,且DE=6,求正方形ABCD的面积
25、如图所示,△ABC是等腰直角三角形,AB=AC,D是斜边BC的中点,E、F分别是AB、AC边上的点,且DE⊥DF,若BE=12,CF=5.求线段EF的长。
26如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.
参考答案:
CC BB AC BD CD CA
13、2√2或√13
14、4
15、7/8
16、33
17、48
18、2
19、135
20、24
21、25
22、2a2
23、25 12
24、256
25、13
26、AO=CQ 直角三角形
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
