3.1.2等式的性质 课件
图片预览









文档简介
(共41张PPT)
3.1.2等式的性质
数学人教版 七年级上
1. 理解、掌握等式的性质. (重点)
2. 能正确应用等式的性质解简单的一元一次方程. (难点)
新知导入
√
用等号表示相等关系的式子叫做等式. 我们可以用
a=b表示一般的等式.
新知导入
√
√
√
√
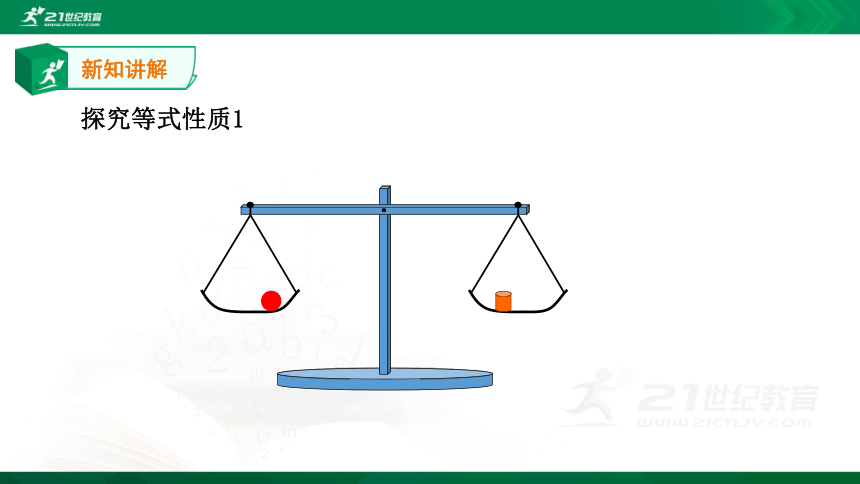
新知讲解
探究等式性质1
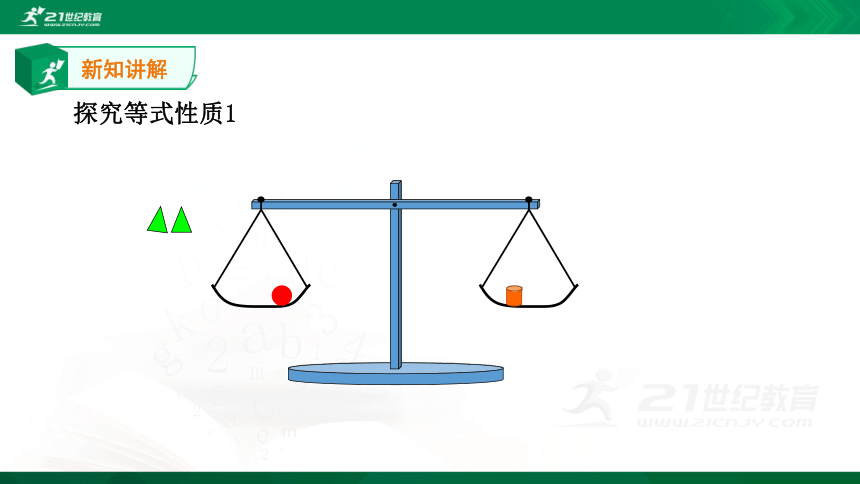
新知讲解
探究等式性质1
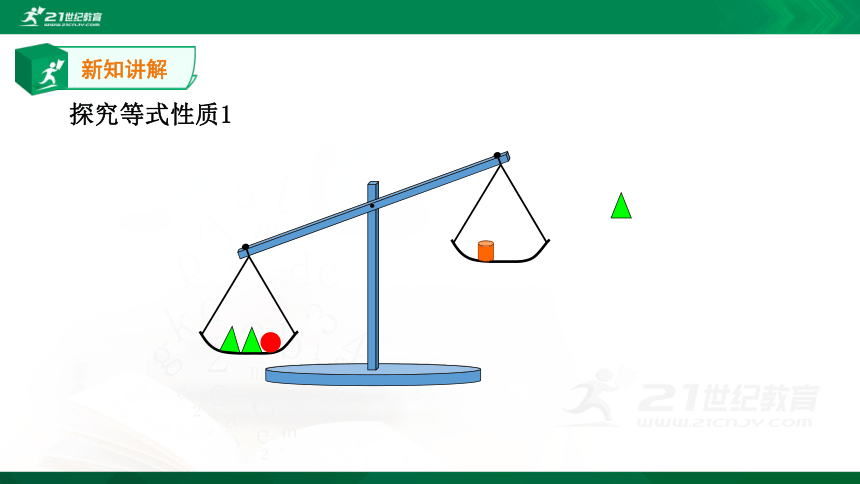
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
等式性质1:
等式两边加(或减)同一个数(或式子),结果仍相等。
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式性质2:
及时小练
1.判断(正确的画“√”,错误的画“×”):
(1)若2a=a+b,则a=b。( )
(2)若x+1=y-2,则x=y-3。( )
(3)等式两边除以同一个数,所得结果仍是等式。( )
(4)若x=y+1,则2x=y+2. ( )
√
×
√
×
2. 已知mx=my,下列结论错误的是( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
A
学以致用
例:利用等式性质解下列方程:
(1)
(2)
(3)
解:两边减7,得
解: 两边除以-5,得
x=-4
解:两边加5,得
x=27
化简,得
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程 的左边,
方程的左右两边相等,所以 x = -27 是原方程的解.
学以致用
小试牛刀
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
A
2. 下列说法正确的是( ) A. 等式都是方程 B. 方程都是等式 C. 不是方程的就不是等式 D. 未知数的值就是方程的解
B
小试牛刀
小试牛刀
4.下面的解法对不对?如果不对,错在哪里?应怎样改正?
(1)解方程:x+12=34
解:x+12=34
x+12 -12=34
x=34
解: x+12=34
x+12 -12=34 -12
x=22
(2)解方程:-9x+3=6
解:-9x+3-3=6-3
于是 -9x=3
所以 x=-3
小试牛刀
解:两边加5,得:
x-5+5=6+5
x=11
解:两边除以0.3 ,得:
0.3x÷0.3=45÷0.3
x=150
解:两边加2,得:
两边乘4,得
x=20
解:两边减4,得:
5x= -4
两边除以5得
本节课你学到了什么?
畅谈收获
性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
用式子可表示为:如果a=b , 那么 a±c=b±c
性质2:等式两边同乘一个数,或除以同一个不为零的数,结果仍相等.
用式子可以表示为,
如果a=b, 那么ac=bc
如果a=b(c≠0),那么
作业布置
课本83页,第4题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
3.1.2等式的性质
数学人教版 七年级上
1. 理解、掌握等式的性质. (重点)
2. 能正确应用等式的性质解简单的一元一次方程. (难点)
新知导入
√
用等号表示相等关系的式子叫做等式. 我们可以用
a=b表示一般的等式.
新知导入
√
√
√
√
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
新知讲解
探究等式性质1
等式性质1:
等式两边加(或减)同一个数(或式子),结果仍相等。
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
新知讲解
探究等式性质2
等式两边乘同一个数,或除以同一个不为0的数,结果仍相等。
等式性质2:
及时小练
1.判断(正确的画“√”,错误的画“×”):
(1)若2a=a+b,则a=b。( )
(2)若x+1=y-2,则x=y-3。( )
(3)等式两边除以同一个数,所得结果仍是等式。( )
(4)若x=y+1,则2x=y+2. ( )
√
×
√
×
2. 已知mx=my,下列结论错误的是( )
A. x=y B. a+mx=a+my
C. mx-y=my-y D. amx=amy
A
学以致用
例:利用等式性质解下列方程:
(1)
(2)
(3)
解:两边减7,得
解: 两边除以-5,得
x=-4
解:两边加5,得
x=27
化简,得
一般地,从方程解出未知数的值以后,可以代入原方程检验,看这个值能否使方程的两边相等.
例如,将 x = -27 代入方程 的左边,
方程的左右两边相等,所以 x = -27 是原方程的解.
学以致用
小试牛刀
3
等式的性质1
-2
-3
-4
等式的性质2
除以-2
减去4
2
A
2. 下列说法正确的是( ) A. 等式都是方程 B. 方程都是等式 C. 不是方程的就不是等式 D. 未知数的值就是方程的解
B
小试牛刀
小试牛刀
4.下面的解法对不对?如果不对,错在哪里?应怎样改正?
(1)解方程:x+12=34
解:x+12=34
x+12 -12=34
x=34
解: x+12=34
x+12 -12=34 -12
x=22
(2)解方程:-9x+3=6
解:-9x+3-3=6-3
于是 -9x=3
所以 x=-3
小试牛刀
解:两边加5,得:
x-5+5=6+5
x=11
解:两边除以0.3 ,得:
0.3x÷0.3=45÷0.3
x=150
解:两边加2,得:
两边乘4,得
x=20
解:两边减4,得:
5x= -4
两边除以5得
本节课你学到了什么?
畅谈收获
性质1:等式两边加(或减)同一个数(或式子),结果仍相等.
用式子可表示为:如果a=b , 那么 a±c=b±c
性质2:等式两边同乘一个数,或除以同一个不为零的数,结果仍相等.
用式子可以表示为,
如果a=b, 那么ac=bc
如果a=b(c≠0),那么
作业布置
课本83页,第4题
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
