24.3.1 锐角三角函数 同步练习(解析版)
文档属性
| 名称 | 24.3.1 锐角三角函数 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-25 10:15:20 | ||
图片预览




文档简介
初中数学华师大版九年级上学期 第24章 24.3.1 锐角三角函数
一、单选题(共4题)
1.如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为(??? ) 21·世纪*教育网
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?2????????????????????????????????????????D.?
3.如图,矩形ABCD的对角线交于点O,已知AB=m,∠BAC=∠α,则下列结论错误的是( ??)
A.?∠BDC=∠α????????????????????B.?BC=m·tanα????????????????????C.?AO= ????????????????????D.?BD=
4.如图,在 中, ,则 sinB 的值为(??? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题(共3题)
5.如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于________. 21教育网
6.如图,在矩形ABCD中, , ,H是AB的中点,将 沿CH折叠,点B落在矩形内点P处,连接AP,则 ________. www-2-1-cnjy-com
7.在 Rt△ABC中, , ,则 ________.
三、计算题(共2题)
8.计算:
9.先化简,再求代数式( - )÷ 的值,其中x=4tan45°+2cos30°.
四、综合题(共2题;共21分)
10.如图,已知△ABC三个顶点的坐标分别为A(-2,-4),B(0,-4),C(1,-1)
(1)请在网格中,画出线段BC关于原点对称的线段B1C1:
(2)请在网格中,过点C画一条直线CD,
将△ABC分成面积相等的两部分,与线段AB相交于点D,写出点D的坐标
(3)若另有一点P(-3,-3),连接PC,则tan∠BCP= ________?。
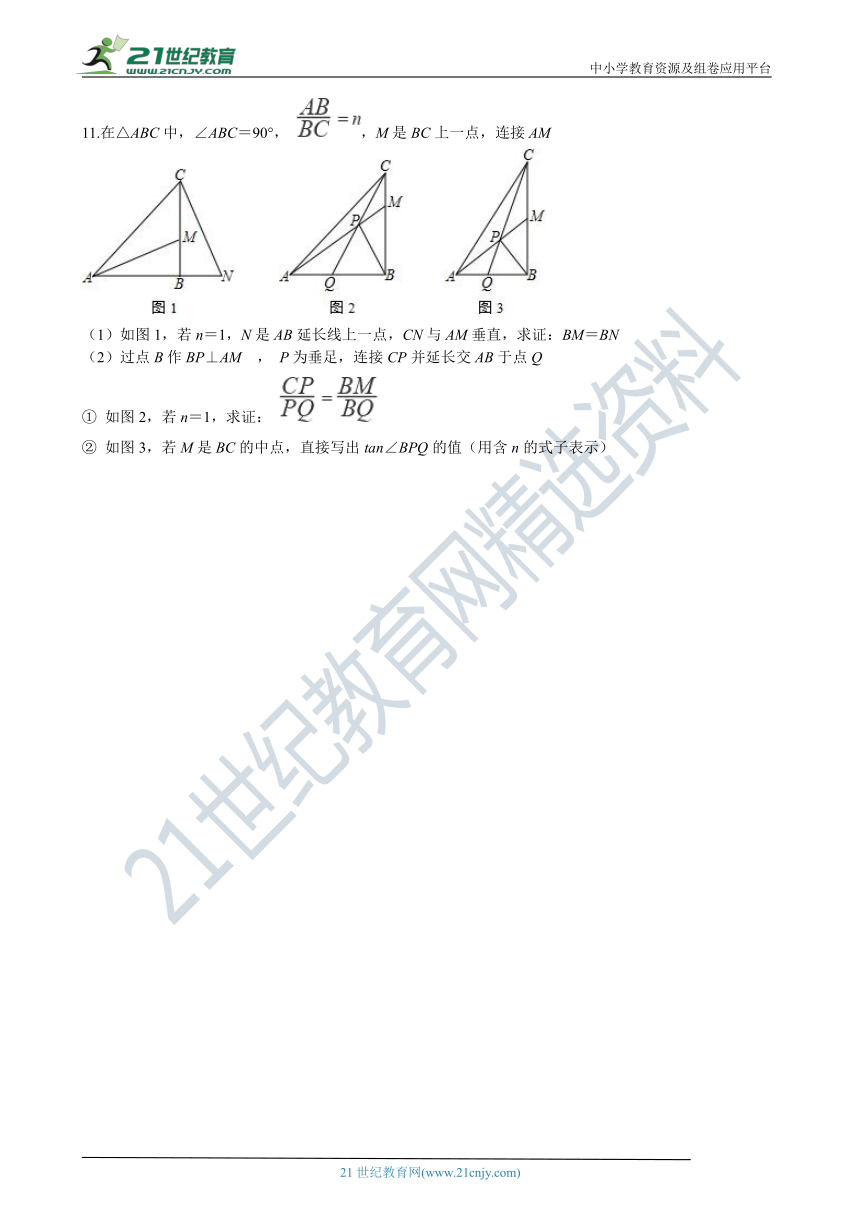
11.在△ABC中,∠ABC=90°, ,M是BC上一点,连接AM
???????? ?????????
(1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN
(2)过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q
① 如图2,若n=1,求证:
② 如图3,若M是BC的中点,直接写出tan∠BPQ的值(用含n的式子表示)
答案解析部分
一、单选题
1. D
解:由图形绕着点D选择可知,当点B与点E重合时,α角度最小且重叠部分为平行四边形,设BC与FD交于点M,如图, www.21-cn-jy.com
依题可得:EF=CD=2,∠F=∠C=90°,∠EMF=∠DMC=α,
∴△EFM≌△DCM(AAS),
∴FM=CM,EM=DM,
设CM=FM=x,则DM=8-x,
在Rt△ABC中,
∵CM2+CD2=DM2 ,
∴x2+22=(8-x)2 ,
解得:x= ,
tanα= .
故答案为:D.
【分析】由图形绕着点D选择可知,当点B与点E重合时,α角度最小且重叠部分为平行四边形,设BC与FD交于点M,根据全等三角形的判定AAS可得△EFM≌△DCM,由全等三角形性质得FM=CM,EM=DM,设CM=FM=x,则DM=8-x,在Rt△ABC中,根据勾股定理列出方程,解之得CD长,再由锐角三角函数正切定义即可求得答案.21世纪教育网版权所有
2. A
解:设 , ,
∵ 点为菱形对角线的交点,
∴ , , ,
∴ ,
把 代入 得 ,
∴ ,
∵四边形 为菱形,
∴ ,
∴ ,解得 ,
∴ ,
在 中, ,
∴ .
故答案为:A.
【分析】设 , ,根据菱形的四边相等得出根据菱形的性质得出, , ,根据线段中点坐标公式,用含m,t的式子表示出点M的坐标,将点M的坐标代入反比例函数的解析式得出 ,根据勾股定理建立方程求解得出,利用等量代换即可简化点M的坐标,在 中,根据正切函数的定义由, 进而即可得出 的值 。21*cnjy*com
3. C
解:A.∵矩形ABCD,
∴AB=DC,∠ABC=∠DCB=90°,
又∵BC=CB,
∴△ABC≌△DCB(SAS),
∴∠BDC=∠BAC=α,
故正确,A不符合题意;
B.∵矩形ABCD,
∴∠ABC=90°,
在Rt△ABC中,
∵∠BAC=α,AB=m,
∴tanα= ,
∴BC=AB·tanα=mtanα,
故正确,B不符合题意;
C.∵矩形ABCD,
∴∠ABC=90°,
在Rt△ABC中,
∵∠BAC=α,AB=m,
∴cosα= ,
∴AC= = ,
∴AO= AC=
故错误,C符合题意;
D.∵矩形ABCD,
∴AC=BD,
由C知AC= = ,
∴BD=AC= ,
故正确,D不符合题意;
故答案为:C.
【分析】A.由矩形性质和全等三角形判定SAS可得△ABC≌△DCB,根据全等三角形性质可得
∠BDC=∠BAC=α,故A正确;
B.由矩形性质得∠ABC=90°,在Rt△ABC中,根据正切函数定义可得BC=AB·tanα=mtanα,
故正确;
C.由矩形性质得∠ABC=90°,在Rt△ABC中,根据余弦函数定义可得AC= = ,再由AO= AC即可求得AO长,故错误;21cnjy.com
D.由矩形性质得AC=BD,由C知AC= = ,从而可得BD长,故正确;
4. D
解:过点A作 ,垂足为D,如图所示.
在 中, ,
;
在 中, ,
,
.
故答案为:D.
【分析】过点A作 ,垂足为D,如图所示.利用解直角三角形可求出CD=1,根据勾股定理可求出AD=, 从而求出BD=CB-CD=3,在Rt△ABD中,利用勾股定理可求出AB的长,利用三角函数定义可求出sinB=的值.2·1·c·n·j·y
二、填空题
5.
解:过点P作PQ⊥AD,垂足为Q,
∵四边形ABCD是平行四边形,
∴DC//AB,
∴∠QDP=∠DAB=60°,
∴PQ=PD?sin∠QDP= PD,
∴ =BP+PQ,
∴当点B、P、Q三点共线时 有最小值,
∴ 的最小值为 。
故答案为:3 。
【分析】过点P作PQ⊥AD,垂足为Q,根据平行四边形的对边平行得出DC//AB,根据二直线平行,同位角相等得出∠QDP=∠DAB=60°,然后根据正弦函数的定义及特殊锐角三角函数值,由PQ=PD?sin∠QDP表示出PQ,故 =BP+PQ,根据两点之间线段最短得出当点B、P、Q三点共线时 有最小值,根据正切函数的定义及特殊锐角三角函数值得出的最小值为 。【来源:21cnj*y.co*m】
6.
解:如图,连接PB,交CH于E,
由折叠可得,CH垂直平分BP, ,
又∵H为AB的中点,
∴ ,
∴ ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
又∵ 中, ,
∴ 。
故答案为: 。
【分析】如图,连接PB,交CH于E,由折叠可得,CH垂直平分BP, ,进而根据线段中点的定义得出, 根据等边对等角及三角形的内角和得出 ;根据同位角相等,二直线平行得出 ,根据二直线平行同位角相等得出, 进而根据正切函数的定义及等角的同名三角函数值相等得出结论。【出处:21教育名师】
7.
解:在 中, ,
故答案为: .
【分析】根据sinA=计算即可.
三、计算题
8. 解:原式
=-1+3-1-6
=-5
【分析】根据有理数的乘方、二次根式的性质、0指数的意义、特殊锐角三角函数值分别化简,再根据实数的运算顺序及法则即可算出答案。21·cn·jy·com
9. 解:原式= = = = x= 原式=
【分析】先将分式的分子分母能分解因式的先分解因式,将括号里的分式减法进行通分计算,再将除法转化为乘法运算,约分化简,同时将x的值进行化简,然后代入求值。 【来源:21·世纪·教育·网】
四、综合题
10. (1)解:如图,作出线段
标字母B1和C1
(2)解:画出直线CD
写出D(-1,-4) (3)1
(3)连接PB,?∵B(0,-4),C(1,-1) P(-3,-3) , ∴PB2=10,PC2=20,CB2=10, ∴PB2+BC2=PC2 , ∴△BPC是等腰直角三角形, ∴∠PCB=45°, ∴tan∠BCP=1. 【分析】(1)先确定点B、C关于原点对称点的位置,然后连接即得线段B1C1. (2)如图,取AB的中点D画出直线CD即可,根据位置写出D点坐标. (3)连接BP,根据勾股定理的逆定理得出△BPC是等腰直角三角形,可得∠PCB=45°,从而求出tan∠BCP的值.2-1-c-n-j-y
11. (1)证明:如图1中,延长AM交CN于点D ? ∵AM⊥CN, ∴∠ADC=90°, ∵∠ABC=∠CBN=90°, ∴∠BAM+∠AMB=90°,∠BCN+∠CMD=90°, ∵∠AMB=∠CMD, ∴∠BAM=∠BCN, ∵ ∴AB=BC 在△ABM和△CBN中 ∴△ABM≌△CBN(ASA), ∴BM=BN. (2)①证明:如图2中,过点C作CH∥AB交BP的延长线于H. ? ∴∠ABC+∠BCH=90° ∵∠ABC=90° ∴∠BCH=∠ABC=90° ∵BP⊥AM, ∴∠BPM=90°, ∴∠MPB+∠AMB=90°,∠MPB+∠H=90°,? ∴∠AMB=∠H, ∵ ∴AB=BC, 在△ABM和△BCH中 ∴△ABM≌△BCH(AAS) ∴BM=CH, ∵CH∥BQ, ∴ ∴ ②如图3中,过点C作CD∥AB交BP的延长线于D,作CE⊥BD于E. ∵点M时BC的中点 ∴BC=2CM 设CM=m,则BC=2m, 则AB=2mn. ∵AB:BC=n ∴AB=2mn, ∵∠DCB=∠ABM=90°,∠D=∠AMB ∴△BCD∽△ABM ∴ 解之:CD=, 在Rt△BCD中,BD= ∵m>0,n>0 ∴BD= 在Rt△AMB中 AM=, ∵S△AMB=AM?BP=AB?BM, ∴PB== ∵S△BCD=BD?CE=CD?BC, ∴CE= ∵CE⊥BD,PM⊥BD, ∴CE∥PM, ∴BM:CM=BP:PE ∵CM=BM, ∴BP=PE ∴PE= ∵∠BPQ=∠CPE, ∴tan∠BPQ=tan∠CPE 在Rt△PCE中, ∴【版权所有:21教育】
【分析】 (1) 如图1中,延长AM交CN于点D,利用垂直的定义及余角的性质,可证得∠BAM=∠BCN,由n=1,可知AB=BC,再利用ASA证明△ABM≌△CBN,然后利用全等三角形的性质可证得结论。 (2)①证明:如图2中,过点C作CH∥AB交BP的延长线于H,利用平行线的性质,可知∠BCH=∠ABC,利用余角的性质,可证∠AMB=∠H,由n=1可得到AB=BC,再利用AAS证明△ABM≌△BCH,从而可得到MB=CH,然后根据平行线分线段成比例定理,得出对应相等成比例,继而可证得结论;②如图3中,过点C作CD∥AB交BP的延长线于D,作CE⊥BD于E,利用线段中点的定义可知BC=2CM,设CM为m,由AB:BC=n可表示出BC、AB,再证明△BCD∽△ABM,利用相似三角形的性质,得出对应边成比例,求出CD,在Rt△BCD和Rt△AMB中,利用勾股定理求出BD,AM,根据同一个直角三角形的面积相等,分别求出PB、CE,再利用平行线分线段成比例,可知BP=PE,就可得到PE的长,根据对顶角相等,可证∠BPQ=∠CPE,然后在Rt△PCE中,利用锐角三角函数的定义,可求出tan∠BPQ。
一、单选题(共4题)
1.如图,有两张矩形纸片ABCD和EFGH、AB=EF=2cm,BC=FG=8cm,把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合,当两张纸片交叉所成的角最小α时,tanα等于(?? )
A.????????????????????????????????????????B.????????????????????????????????????????C.????????????????????????????????????????D.?
2.如图,在平面直角坐标系 中,菱形 的顶点 与原点 重合,顶点 落在 轴的正半轴上,对角线 、 交于点 ,点 、 恰好都在反比例函数 的图象上,则 的值为(??? ) 21·世纪*教育网
A.?????????????????????????????????????????B.?????????????????????????????????????????C.?2????????????????????????????????????????D.?
3.如图,矩形ABCD的对角线交于点O,已知AB=m,∠BAC=∠α,则下列结论错误的是( ??)
A.?∠BDC=∠α????????????????????B.?BC=m·tanα????????????????????C.?AO= ????????????????????D.?BD=
4.如图,在 中, ,则 sinB 的值为(??? )
A.???????????????????????????????????B.???????????????????????????????????C.???????????????????????????????????D.?
二、填空题(共3题)
5.如图,平行四边形ABCD中,∠DAB=60°,AB=6,BC=2,P为边CD上的一动点,则 的最小值等于________. 21教育网
6.如图,在矩形ABCD中, , ,H是AB的中点,将 沿CH折叠,点B落在矩形内点P处,连接AP,则 ________. www-2-1-cnjy-com
7.在 Rt△ABC中, , ,则 ________.
三、计算题(共2题)
8.计算:
9.先化简,再求代数式( - )÷ 的值,其中x=4tan45°+2cos30°.
四、综合题(共2题;共21分)
10.如图,已知△ABC三个顶点的坐标分别为A(-2,-4),B(0,-4),C(1,-1)
(1)请在网格中,画出线段BC关于原点对称的线段B1C1:
(2)请在网格中,过点C画一条直线CD,
将△ABC分成面积相等的两部分,与线段AB相交于点D,写出点D的坐标
(3)若另有一点P(-3,-3),连接PC,则tan∠BCP= ________?。
11.在△ABC中,∠ABC=90°, ,M是BC上一点,连接AM
???????? ?????????
(1)如图1,若n=1,N是AB延长线上一点,CN与AM垂直,求证:BM=BN
(2)过点B作BP⊥AM , P为垂足,连接CP并延长交AB于点Q
① 如图2,若n=1,求证:
② 如图3,若M是BC的中点,直接写出tan∠BPQ的值(用含n的式子表示)
答案解析部分
一、单选题
1. D
解:由图形绕着点D选择可知,当点B与点E重合时,α角度最小且重叠部分为平行四边形,设BC与FD交于点M,如图, www.21-cn-jy.com
依题可得:EF=CD=2,∠F=∠C=90°,∠EMF=∠DMC=α,
∴△EFM≌△DCM(AAS),
∴FM=CM,EM=DM,
设CM=FM=x,则DM=8-x,
在Rt△ABC中,
∵CM2+CD2=DM2 ,
∴x2+22=(8-x)2 ,
解得:x= ,
tanα= .
故答案为:D.
【分析】由图形绕着点D选择可知,当点B与点E重合时,α角度最小且重叠部分为平行四边形,设BC与FD交于点M,根据全等三角形的判定AAS可得△EFM≌△DCM,由全等三角形性质得FM=CM,EM=DM,设CM=FM=x,则DM=8-x,在Rt△ABC中,根据勾股定理列出方程,解之得CD长,再由锐角三角函数正切定义即可求得答案.21世纪教育网版权所有
2. A
解:设 , ,
∵ 点为菱形对角线的交点,
∴ , , ,
∴ ,
把 代入 得 ,
∴ ,
∵四边形 为菱形,
∴ ,
∴ ,解得 ,
∴ ,
在 中, ,
∴ .
故答案为:A.
【分析】设 , ,根据菱形的四边相等得出根据菱形的性质得出, , ,根据线段中点坐标公式,用含m,t的式子表示出点M的坐标,将点M的坐标代入反比例函数的解析式得出 ,根据勾股定理建立方程求解得出,利用等量代换即可简化点M的坐标,在 中,根据正切函数的定义由, 进而即可得出 的值 。21*cnjy*com
3. C
解:A.∵矩形ABCD,
∴AB=DC,∠ABC=∠DCB=90°,
又∵BC=CB,
∴△ABC≌△DCB(SAS),
∴∠BDC=∠BAC=α,
故正确,A不符合题意;
B.∵矩形ABCD,
∴∠ABC=90°,
在Rt△ABC中,
∵∠BAC=α,AB=m,
∴tanα= ,
∴BC=AB·tanα=mtanα,
故正确,B不符合题意;
C.∵矩形ABCD,
∴∠ABC=90°,
在Rt△ABC中,
∵∠BAC=α,AB=m,
∴cosα= ,
∴AC= = ,
∴AO= AC=
故错误,C符合题意;
D.∵矩形ABCD,
∴AC=BD,
由C知AC= = ,
∴BD=AC= ,
故正确,D不符合题意;
故答案为:C.
【分析】A.由矩形性质和全等三角形判定SAS可得△ABC≌△DCB,根据全等三角形性质可得
∠BDC=∠BAC=α,故A正确;
B.由矩形性质得∠ABC=90°,在Rt△ABC中,根据正切函数定义可得BC=AB·tanα=mtanα,
故正确;
C.由矩形性质得∠ABC=90°,在Rt△ABC中,根据余弦函数定义可得AC= = ,再由AO= AC即可求得AO长,故错误;21cnjy.com
D.由矩形性质得AC=BD,由C知AC= = ,从而可得BD长,故正确;
4. D
解:过点A作 ,垂足为D,如图所示.
在 中, ,
;
在 中, ,
,
.
故答案为:D.
【分析】过点A作 ,垂足为D,如图所示.利用解直角三角形可求出CD=1,根据勾股定理可求出AD=, 从而求出BD=CB-CD=3,在Rt△ABD中,利用勾股定理可求出AB的长,利用三角函数定义可求出sinB=的值.2·1·c·n·j·y
二、填空题
5.
解:过点P作PQ⊥AD,垂足为Q,
∵四边形ABCD是平行四边形,
∴DC//AB,
∴∠QDP=∠DAB=60°,
∴PQ=PD?sin∠QDP= PD,
∴ =BP+PQ,
∴当点B、P、Q三点共线时 有最小值,
∴ 的最小值为 。
故答案为:3 。
【分析】过点P作PQ⊥AD,垂足为Q,根据平行四边形的对边平行得出DC//AB,根据二直线平行,同位角相等得出∠QDP=∠DAB=60°,然后根据正弦函数的定义及特殊锐角三角函数值,由PQ=PD?sin∠QDP表示出PQ,故 =BP+PQ,根据两点之间线段最短得出当点B、P、Q三点共线时 有最小值,根据正切函数的定义及特殊锐角三角函数值得出的最小值为 。【来源:21cnj*y.co*m】
6.
解:如图,连接PB,交CH于E,
由折叠可得,CH垂直平分BP, ,
又∵H为AB的中点,
∴ ,
∴ ,
∴ , ,
又∵ ,
∴ ,
∴ ,
∴ ,
∴ ,
又∵ 中, ,
∴ 。
故答案为: 。
【分析】如图,连接PB,交CH于E,由折叠可得,CH垂直平分BP, ,进而根据线段中点的定义得出, 根据等边对等角及三角形的内角和得出 ;根据同位角相等,二直线平行得出 ,根据二直线平行同位角相等得出, 进而根据正切函数的定义及等角的同名三角函数值相等得出结论。【出处:21教育名师】
7.
解:在 中, ,
故答案为: .
【分析】根据sinA=计算即可.
三、计算题
8. 解:原式
=-1+3-1-6
=-5
【分析】根据有理数的乘方、二次根式的性质、0指数的意义、特殊锐角三角函数值分别化简,再根据实数的运算顺序及法则即可算出答案。21·cn·jy·com
9. 解:原式= = = = x= 原式=
【分析】先将分式的分子分母能分解因式的先分解因式,将括号里的分式减法进行通分计算,再将除法转化为乘法运算,约分化简,同时将x的值进行化简,然后代入求值。 【来源:21·世纪·教育·网】
四、综合题
10. (1)解:如图,作出线段
标字母B1和C1
(2)解:画出直线CD
写出D(-1,-4) (3)1
(3)连接PB,?∵B(0,-4),C(1,-1) P(-3,-3) , ∴PB2=10,PC2=20,CB2=10, ∴PB2+BC2=PC2 , ∴△BPC是等腰直角三角形, ∴∠PCB=45°, ∴tan∠BCP=1. 【分析】(1)先确定点B、C关于原点对称点的位置,然后连接即得线段B1C1. (2)如图,取AB的中点D画出直线CD即可,根据位置写出D点坐标. (3)连接BP,根据勾股定理的逆定理得出△BPC是等腰直角三角形,可得∠PCB=45°,从而求出tan∠BCP的值.2-1-c-n-j-y
11. (1)证明:如图1中,延长AM交CN于点D ? ∵AM⊥CN, ∴∠ADC=90°, ∵∠ABC=∠CBN=90°, ∴∠BAM+∠AMB=90°,∠BCN+∠CMD=90°, ∵∠AMB=∠CMD, ∴∠BAM=∠BCN, ∵ ∴AB=BC 在△ABM和△CBN中 ∴△ABM≌△CBN(ASA), ∴BM=BN. (2)①证明:如图2中,过点C作CH∥AB交BP的延长线于H. ? ∴∠ABC+∠BCH=90° ∵∠ABC=90° ∴∠BCH=∠ABC=90° ∵BP⊥AM, ∴∠BPM=90°, ∴∠MPB+∠AMB=90°,∠MPB+∠H=90°,? ∴∠AMB=∠H, ∵ ∴AB=BC, 在△ABM和△BCH中 ∴△ABM≌△BCH(AAS) ∴BM=CH, ∵CH∥BQ, ∴ ∴ ②如图3中,过点C作CD∥AB交BP的延长线于D,作CE⊥BD于E. ∵点M时BC的中点 ∴BC=2CM 设CM=m,则BC=2m, 则AB=2mn. ∵AB:BC=n ∴AB=2mn, ∵∠DCB=∠ABM=90°,∠D=∠AMB ∴△BCD∽△ABM ∴ 解之:CD=, 在Rt△BCD中,BD= ∵m>0,n>0 ∴BD= 在Rt△AMB中 AM=, ∵S△AMB=AM?BP=AB?BM, ∴PB== ∵S△BCD=BD?CE=CD?BC, ∴CE= ∵CE⊥BD,PM⊥BD, ∴CE∥PM, ∴BM:CM=BP:PE ∵CM=BM, ∴BP=PE ∴PE= ∵∠BPQ=∠CPE, ∴tan∠BPQ=tan∠CPE 在Rt△PCE中, ∴【版权所有:21教育】
【分析】 (1) 如图1中,延长AM交CN于点D,利用垂直的定义及余角的性质,可证得∠BAM=∠BCN,由n=1,可知AB=BC,再利用ASA证明△ABM≌△CBN,然后利用全等三角形的性质可证得结论。 (2)①证明:如图2中,过点C作CH∥AB交BP的延长线于H,利用平行线的性质,可知∠BCH=∠ABC,利用余角的性质,可证∠AMB=∠H,由n=1可得到AB=BC,再利用AAS证明△ABM≌△BCH,从而可得到MB=CH,然后根据平行线分线段成比例定理,得出对应相等成比例,继而可证得结论;②如图3中,过点C作CD∥AB交BP的延长线于D,作CE⊥BD于E,利用线段中点的定义可知BC=2CM,设CM为m,由AB:BC=n可表示出BC、AB,再证明△BCD∽△ABM,利用相似三角形的性质,得出对应边成比例,求出CD,在Rt△BCD和Rt△AMB中,利用勾股定理求出BD,AM,根据同一个直角三角形的面积相等,分别求出PB、CE,再利用平行线分线段成比例,可知BP=PE,就可得到PE的长,根据对顶角相等,可证∠BPQ=∠CPE,然后在Rt△PCE中,利用锐角三角函数的定义,可求出tan∠BPQ。
