北师大版数学八年级上一次函数复习课件(共28张ppt)
文档属性
| 名称 | 北师大版数学八年级上一次函数复习课件(共28张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-10-26 07:45:29 | ||
图片预览





文档简介
(共28张PPT)
一、知识要点:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,_
__),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
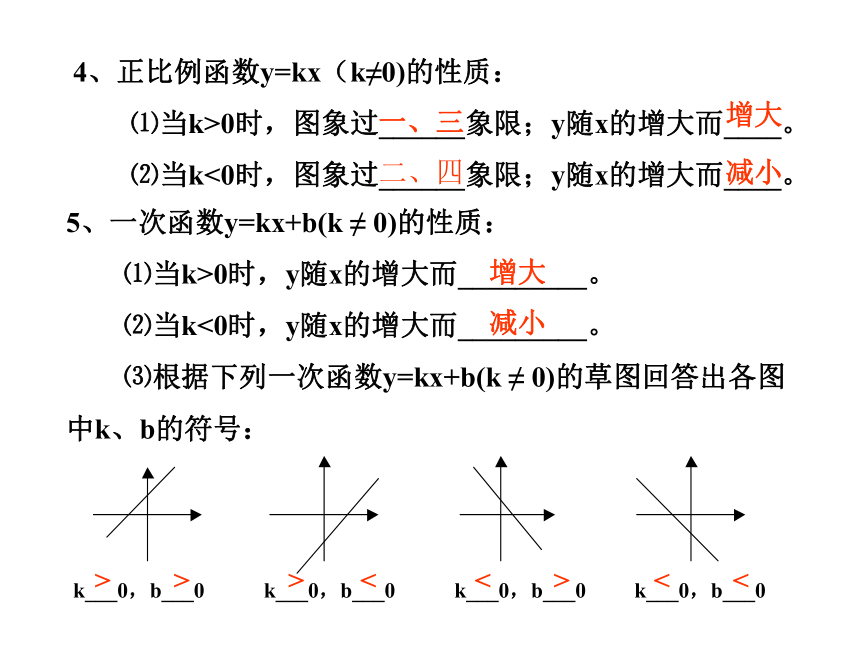
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
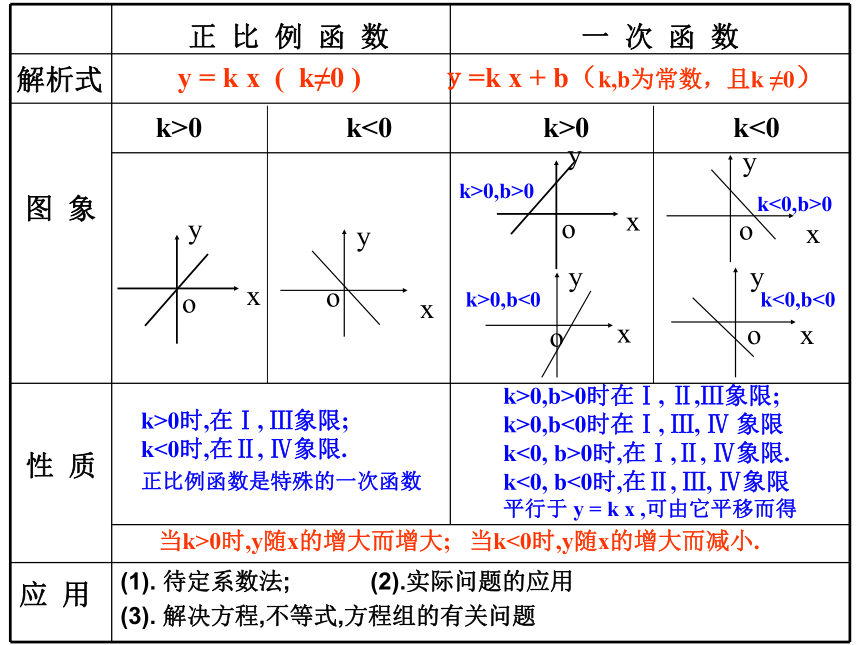
一 次 函 数
正 比 例 函 数
解析式
图 象
性 质
应 用
y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0)
k>0 k<0 k>0 k<0
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
y
x
o
x
y
o
k>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数
k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得
当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
(1). 待定系数法; (2).实际问题的应用
(3). 解决方程,不等式,方程组的有关问题
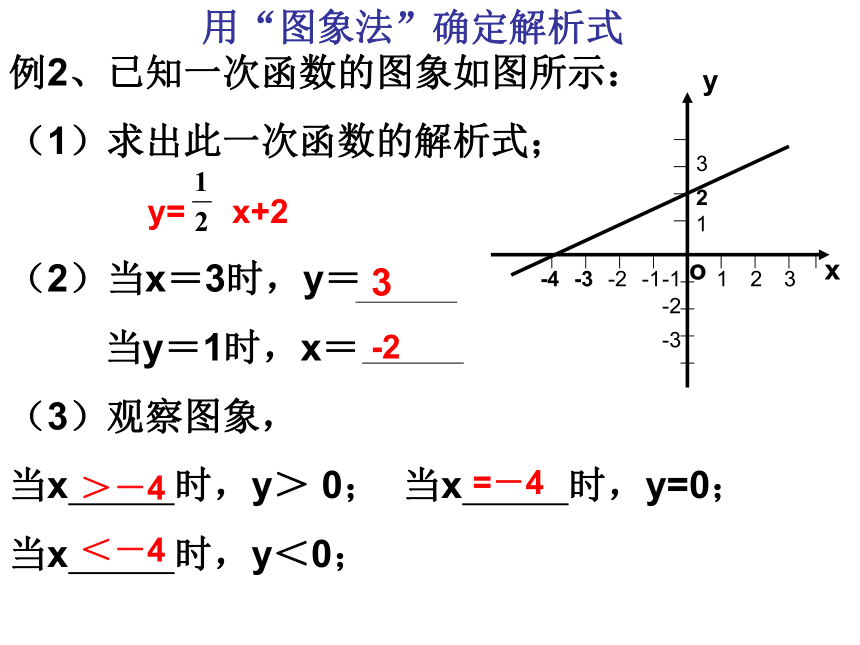
例1、已知
①y是x一次函数。
则当m、n满足什么条件时:
②y是x正比例函数。
>-4
=-4
<-4
3
-2
用“图象法”确定解析式
②
①、②、③
④
③
(2)、如果一次函数y=kx-3k+6的图象经过原点,那么
k的值为________。
(3)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
k=2
解:设一次函数解析式为y=kx+b,
把x=1时, y=5;x=6时,y=0代入解析式,得
解得
∴一次函数的解析式为 y= - x+6。
点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
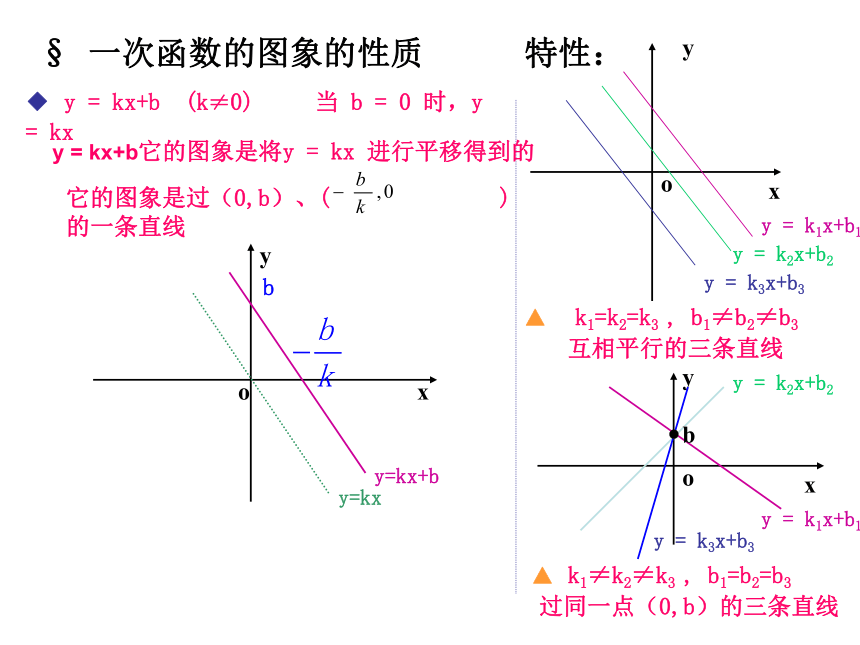
§ 一次函数的图象的性质
◆ y = kx+b (k≠0) 当 b = 0 时,y = kx
x
y
o
b
特性:
x
y
o
y = k1x+b1
y = k2x+b2
y = k3x+b3
▲ k1=k2=k3 , b1≠b2≠b3
互相平行的三条直线
x
y
o
y = k2x+b2
y = k3x+b3
b
●
▲ k1≠k2≠k3 , b1=b2=b3
过同一点(0,b)的三条直线
y=kx
y=kx+b
y = kx+b它的图象是将y = kx 进行平移得到的
y = k1x+b1
2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
图象辨析
A
3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
C
4、直线y1=ax+b与直线y2=bx+a在同一坐标系内的大致图象是 ( )
a>0 ,b>0
b<0, a>0
a>0 ,b>0
b>0, a<0
a>0 ,b>0
b<0, a<0
a>0 ,b>0
b>0, a>0
D
2、根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
1、有下列函数:①y=2x+1, ②y=-3x+4,③y=0.5x,④y=x-6;
① ④
②
③
①
函数y随x的增大而增大的是__________;
其中过原点的直线是________;
函数y随x的增大而减小的是___________;
图象在第一、二、三象限的是________ 。
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A
C
B
D
D
y/毫安
x/天
此种手机的电板最大带电量是多少?
1、某手机的电板剩余电量y毫安是使用天数x的一次函数x和y关系如图 :
小 试 牛 刀
2、某植物t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
l
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm?
(4)先写出y与t的关系式,
再计算长到100cm需几天?
初生牛犊不怕虎
3、 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量的关系如图:
旅客最多可免费携带多少千克行李?
⑵超过30千克后,每千克需付多少元?
⑴想一想紫红色那段图象表示什么意思?
生活中的数学
4、 下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。
做一做
新龟兔赛跑
s /米
(1)这一次是 米赛跑。
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(2)表示兔子的图象是 。
-1
12
9
10
11
-3
-2
100
l2
-4
根据图象可以知道:
s /米
(3)当兔子到达终点时,乌龟距终点还有 米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米。
(5)乌龟要先到达终点,至少要比兔子早跑 分钟。
-1
12
9
10
11
-3
-2
40
4
-4
你还能用其他方法解决上述问题吗?
40
是哪个队获胜了?
5、10千米龙舟比赛中,红队由于某些原因,晚出发了。出发时蓝队已经划出了 500米,如图所示,?和m分别表示蓝队和红队的行驶路程y(千米)和时间x(分)之间的关系。
y(千米)
x(分)
m
2
4
6
8
5
10
15
20
25
0
?
6、已知:函数y = (m+1) x+2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与此同时y = ﹣3 x + 1 的交点
并求这两条直线 与y 轴所围成的三角形面积
解:(1)由题意:
2=﹣(m+1)+2m﹣6
解得 m = 9
∴ y = 10x+12
(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
解得: x =1 , y = ﹣2
∴ 这两直线的交点是(1 ,﹣2)
y = 2x﹣4 与y 轴交于( 0 , 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)
●
x
y
o
1
1
﹣4
(1, ﹣2)
S△=
-2
小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:
观察图象形状,有何特点,你知道该电话套餐的内容吗?
⑴该话费套餐的月租费是多少元?
⑵每分钟通话需多少元?
100分钟后每分钟通话:
100分钟前每分钟通话:
思考:
练习2、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(2)服药5时,血液中含药量为每毫升____毫克。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(3)当x≤2时y与x之间的函数关系式是_____。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(4)当x≥2时y与x之间的函数关系式是____。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间范围是___时。.
一、知识要点:
1、一次函数的概念:函数y=_______(k、b为常数,k______)叫做一次函数。当b_____时,函数y=____(k____)叫做正比例函数。
kx +b
≠0
= 0
≠0
kx
★理解一次函数概念应注意下面两点:
⑴、解析式中自变量x的次数是___次,⑵、比例系数_____。
1
K≠0
2、正比例函数y=kx(k≠0)的图象是过点(_____),(______)的_________。
3、一次函数y=kx+b(k≠0)的图象是过点(0,_
__),(____,0)的__________。
0,0
1,k
一条直线
b
一条直线
4、正比例函数y=kx(k≠0)的性质:
⑴当k>0时,图象过______象限;y随x的增大而____。
⑵当k<0时,图象过______象限;y随x的增大而____。
一、三
增大
二、四
减小
5、一次函数y=kx+b(k ≠ 0)的性质:
⑴当k>0时,y随x的增大而_________。
⑵当k<0时,y随x的增大而_________。
⑶根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图
中k、b的符号:
增大
减小
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
<
<
>
<
<
>
>
>
一 次 函 数
正 比 例 函 数
解析式
图 象
性 质
应 用
y = k x ( k≠0 ) y=k x + b(k,b为常数,且k ≠0)
k>0 k<0 k>0 k<0
k>0,b>0
k>0,b<0
k<0,b>0
k<0,b<0
y
x
o
x
y
o
k>0时,在Ⅰ, Ⅲ象限;
k<0时,在Ⅱ, Ⅳ象限.
正比例函数是特殊的一次函数
k>0,b>0时在Ⅰ, Ⅱ,Ⅲ象限;
k>0,b<0时在Ⅰ, Ⅲ, Ⅳ 象限
k<0, b>0时,在Ⅰ,Ⅱ, Ⅳ象限.
k<0, b<0时,在Ⅱ, Ⅲ, Ⅳ象限
平行于 y = k x ,可由它平移而得
当k>0时,y随x的增大而增大; 当k<0时,y随x的增大而减小.
(1). 待定系数法; (2).实际问题的应用
(3). 解决方程,不等式,方程组的有关问题
例1、已知
①y是x一次函数。
则当m、n满足什么条件时:
②y是x正比例函数。
>-4
=-4
<-4
3
-2
用“图象法”确定解析式
②
①、②、③
④
③
(2)、如果一次函数y=kx-3k+6的图象经过原点,那么
k的值为________。
(3)、已知y-1与x成正比例,且x=-2时,y=4,那么y与
x之间的函数关系式为_________________。
k=2
解:设一次函数解析式为y=kx+b,
把x=1时, y=5;x=6时,y=0代入解析式,得
解得
∴一次函数的解析式为 y= - x+6。
点评:用待定系数法求一次函数y=kx+b的解析式,可由已知条件给出的两对x、y的值,列出关于k、b的二元一次方程组。由此求出k、b的值,就可以得到所求的一次函数的解析式。
例2、已知一次函数y=kx+b(k≠0)在x=1时,y=5,且
它的图象与x轴交点的横坐标是6,求这个一次函数的
解析式。
§ 一次函数的图象的性质
◆ y = kx+b (k≠0) 当 b = 0 时,y = kx
x
y
o
b
特性:
x
y
o
y = k1x+b1
y = k2x+b2
y = k3x+b3
▲ k1=k2=k3 , b1≠b2≠b3
互相平行的三条直线
x
y
o
y = k2x+b2
y = k3x+b3
b
●
▲ k1≠k2≠k3 , b1=b2=b3
过同一点(0,b)的三条直线
y=kx
y=kx+b
y = kx+b它的图象是将y = kx 进行平移得到的
y = k1x+b1
2、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是( )
1.已知一次函数y=kx+b,y随着x的增大而减小,且kb<0,则在直角坐标系内它的大致图象是( )
(A) (B) (C) (D)
A
图象辨析
A
3.直线y1=kx与直线y2=kx-k在同一坐标系内的大致图象是( )
k>0
k<0
k<0
不平行
k>0 -k>0
k<0 -k<0
k<0 -k>0
C
4、直线y1=ax+b与直线y2=bx+a在同一坐标系内的大致图象是 ( )
a>0 ,b>0
b<0, a>0
a>0 ,b>0
b>0, a<0
a>0 ,b>0
b<0, a<0
a>0 ,b>0
b>0, a>0
D
2、根据下列一次函数y=kx+b(k ≠ 0)的草图回答出各图中k、b的符号:
k___0,b___0 k___0,b___0 k___0,b___0 k___0,b___0
1、有下列函数:①y=2x+1, ②y=-3x+4,③y=0.5x,④y=x-6;
① ④
②
③
①
函数y随x的增大而增大的是__________;
其中过原点的直线是________;
函数y随x的增大而减小的是___________;
图象在第一、二、三象限的是________ 。
一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h(厘米)与燃烧时间t(时)的函数关系的图象是( )
A
C
B
D
D
y/毫安
x/天
此种手机的电板最大带电量是多少?
1、某手机的电板剩余电量y毫安是使用天数x的一次函数x和y关系如图 :
小 试 牛 刀
2、某植物t天后的高度为ycm,图中反映了y与t之间的关系,根据图象回答下列问题:
(1)植物刚栽的时候多高?
9
6
3
12
15
18
21
24
l
2
4
6
8
10
12
14
t/天
Y cm
(2)3天后该植物高度为多少?
(3)几天后该植物高度可达21cm?
(4)先写出y与t的关系式,
再计算长到100cm需几天?
初生牛犊不怕虎
3、 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量的关系如图:
旅客最多可免费携带多少千克行李?
⑵超过30千克后,每千克需付多少元?
⑴想一想紫红色那段图象表示什么意思?
生活中的数学
4、 下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。
做一做
新龟兔赛跑
s /米
(1)这一次是 米赛跑。
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(2)表示兔子的图象是 。
-1
12
9
10
11
-3
-2
100
l2
-4
根据图象可以知道:
s /米
(3)当兔子到达终点时,乌龟距终点还有 米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米。
(5)乌龟要先到达终点,至少要比兔子早跑 分钟。
-1
12
9
10
11
-3
-2
40
4
-4
你还能用其他方法解决上述问题吗?
40
是哪个队获胜了?
5、10千米龙舟比赛中,红队由于某些原因,晚出发了。出发时蓝队已经划出了 500米,如图所示,?和m分别表示蓝队和红队的行驶路程y(千米)和时间x(分)之间的关系。
y(千米)
x(分)
m
2
4
6
8
5
10
15
20
25
0
?
6、已知:函数y = (m+1) x+2 m﹣6
(1)若函数图象过(﹣1 ,2),求此函数的解析式。
(2)若函数图象与直线 y = 2 x + 5 平行,求其函数的解析式。
(3)求满足(2)条件的直线与此同时y = ﹣3 x + 1 的交点
并求这两条直线 与y 轴所围成的三角形面积
解:(1)由题意:
2=﹣(m+1)+2m﹣6
解得 m = 9
∴ y = 10x+12
(2) 由题意,m +1= 2
解得 m = 1
∴ y = 2x﹣4
(3) 由题意得
解得: x =1 , y = ﹣2
∴ 这两直线的交点是(1 ,﹣2)
y = 2x﹣4 与y 轴交于( 0 , 4 )
y = ﹣3x + 1与y 轴交于( 0 , 1)
●
x
y
o
1
1
﹣4
(1, ﹣2)
S△=
-2
小明在电信局办理了某种电话话费套餐,该套餐要求按分钟计费且无论通话多长时间都需要交纳一定的费用作为月租费,办理后某月手机话费y元和通话时间x的关系图如下:
观察图象形状,有何特点,你知道该电话套餐的内容吗?
⑴该话费套餐的月租费是多少元?
⑵每分钟通话需多少元?
100分钟后每分钟通话:
100分钟前每分钟通话:
思考:
练习2、某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(2)服药5时,血液中含药量为每毫升____毫克。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(3)当x≤2时y与x之间的函数关系式是_____。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(4)当x≥2时y与x之间的函数关系式是____。
某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后。
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间范围是___时。.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
