2.3 透镜成像 凸透镜成像 教案
图片预览
文档简介
凸 透 镜 成 像
1.教学目标
知识与技能
过程与方法
能识别凸透镜和凹透镜
知道凸透镜的会聚作用和凹透镜的发散作用
知道透镜的主光轴、光心、焦点和焦距
理解凸透镜成像的初步规律
知道照相机、幻灯机、放大镜的成像原理
领会研究凸透镜成像的方法,感受验证过程的科学方法
学会验证凸透镜成像的规律
能运用凸透镜成像规律讨论、解决一些简单的实际问题
2.知识网络图
结构:中间厚、边缘薄
凸透镜
对光线的作用:会聚
(1)透镜 结构:中间薄、边缘厚
凹透镜
对光线的作用:发散
验证凸透镜成像的方法
成像规律 验证过程的科学方法
运用规律解决实际问题
(2)凸透镜成像
照相机
成像应用 幻灯机
放大镜
经典例题类析
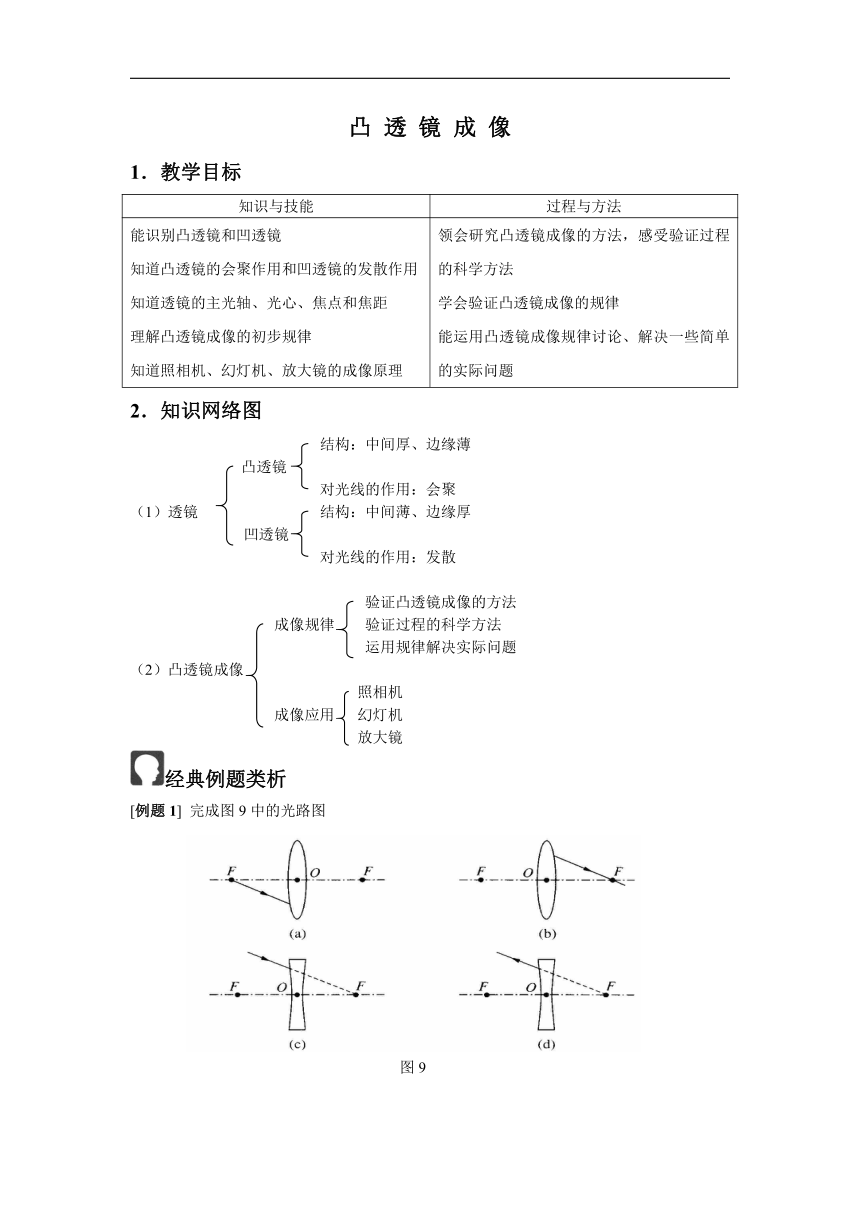
[例题1] 完成图9中的光路图
?
解析:图9中所给的四个透镜,(a)、(b)是凸透镜,(c)、(d)为凹透镜,并且(a)、(c)给出入射光线,要求画出折射光线。而(b)、(d)则给出折射光线,要求画出入射光线。根据光心、焦点的定义方法就能画出这些特殊光线。
在画图中要注意光的传播方向。 (利用基本概念完成作图)
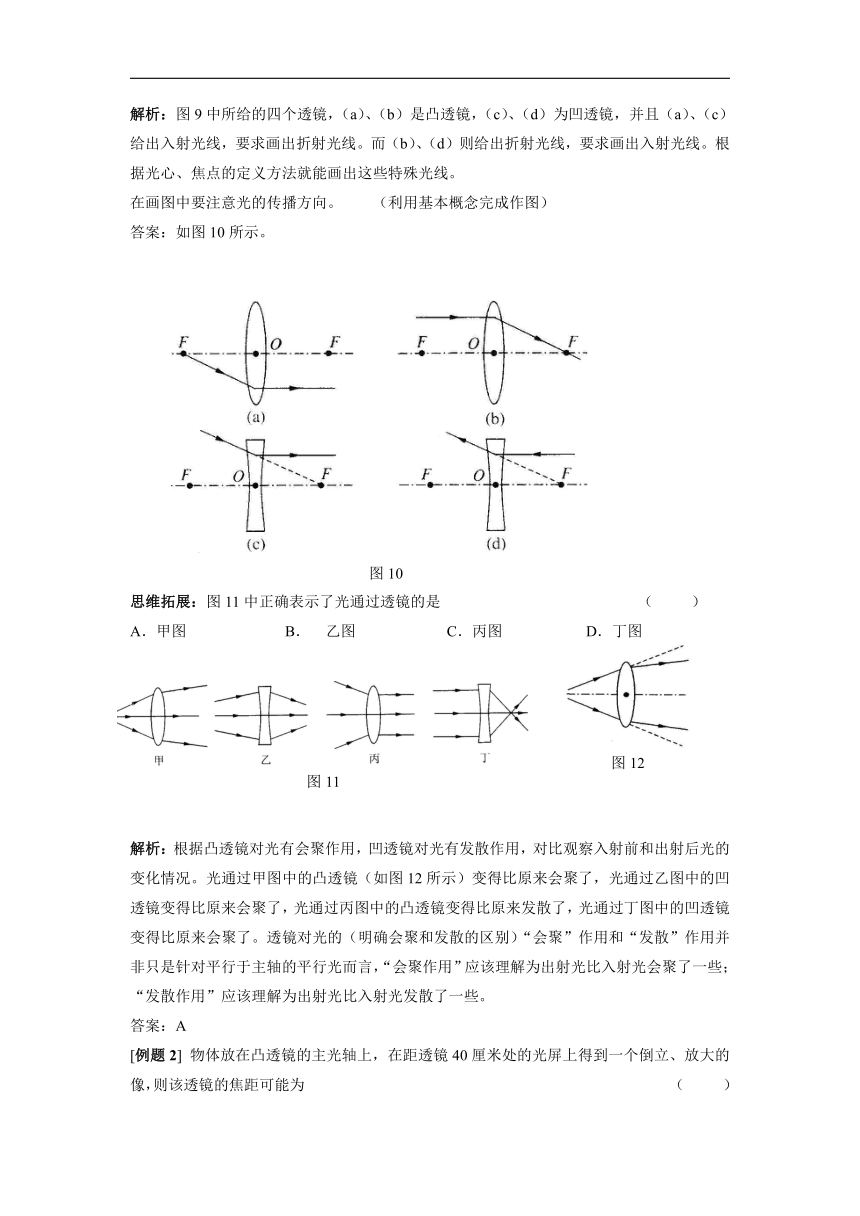
答案:如图10所示。
思维拓展:图11中正确表示了光通过透镜的是 ( )
A.甲图 B. 乙图 C.丙图 D.丁图
x*k.Com]
解析:根据凸透镜对光有会聚作用,凹透镜对光有发散作用,对比观察入射前和出射后光的变化情况。光通过甲图中的凸透镜(如图12所示)变得比原来会聚了,光通过乙图中的凹透镜变得比原来会聚了,光通过丙图中的凸透镜变得比原来发散了,光通过丁图中的凹透镜变得比原来会聚了。透镜对光的(明确会聚和发散的区别)“会聚”作用和“发散”作用并非只是针对平行于主轴的平行光而言,“会聚作用”应该理解为出射光比入射光会聚了一些;“发散作用”应该理解为出射光比入射光发散了一些。
答案:A
[例题2] 物体放在凸透镜的主光轴上,在距透镜40厘米处的光屏上得到一个倒立、放大的像,则该透镜的焦距可能为 ( )
A.40cm B.30cm C.20cm 10.5cm
解析:本题可以用“不等式法”来确定焦距的范围。根据题意“距透镜40厘米处的光屏”,可知像距v,且所得的像是倒立、放大的,根据凸透镜成像的规律得v>2f,即40厘米>2f,由此推得该凸透镜的焦距f<20厘米,符合这一要求的只有选项D。
答案:D
思维拓展1:物体距凸透镜20cm时,可在光屏上得到一个缩小的实像,若把物体向透镜方向移8cm,又可在光屏上得到一个放大的实像,则透镜的焦距是 ( )
A.20cm B.10cm C.9cm D.5cm
解析:根据题意,当物距u=20cm时,物体通过凸透镜在光屏上成倒立、缩小的实像。即物距必须满足u>2f,也就是f<10cm。这是焦距的第一个解。又从题意可知:把物体向透镜方向移8cm,所以当物距u=12cm时,物体通过凸透镜在光屏上成倒立、放大的实像。即物距必须满足2f>u>f,也就是2f>12cm>f ,求得12cm>f>6cm。这是焦距的第二个解。选取两个解的公共部分,求得最后结果为10cm>f>6cm。因此选C正确。
答案:C (注意:物体移动时的分析方法)
思维拓展2:物体距凸透镜30厘米时,在距透镜20厘米处的光屏上成一清晰的像,由此可以确定该凸透镜的焦距可能为 ( )
A.f=10cm B.f=15cm C.15cm>f>10cm D.无法确定
解析:本题有两种解法:
解法一:“不等式法”。由题意可知,光屏上成清晰的像,必定是实像,但到底是缩小的像还是放大的像,有的学生就分辨不清,故直接错选了“D”。其实物距30厘米大于像距20厘米,所以光屏上像是缩小的,物距30 cm>2f,求得f<15cm;而像距v满足:2f>20cm>f,求得20cm>f>10cm,取两个解的公共部分,得最后结果为15cm>f>10cm。因此选C正确。
解法二:“公式法”。根据题意,物距u=30cm时,像距v=20cm,直接带入凸透镜成像公式:1/u+ 1/v = 1/f,即1/30cm+1/20cm=1/f,求解得:f=12cm。因此选C正确。
答案:C(注意方法的灵活运用)
[例题3] 物体放在凸透镜前20厘米处,在透镜另一侧的光屏上成一个倒立放大的像。当物体距凸透镜12厘米时,所成的像 ( )
A.一定是倒立放大的实像 B.可能是倒立缩小的实像
C.可能是正立放大的虚像 D.可能是正立等大的虚像
解析:本题可以用“不等式法”先确定焦距的范围。由题意可知,当物距u=12cm时,物体通过凸透镜在光屏上成倒立放大的实像。即物距必须满足2f>u>f,也就是2f>20cm>f ,求得20cm>f>10cm。当物体离透镜12cm时,解题的关键是判断12cm与焦距f的关系,,较简单可行的方法是“特殊值法”。由于20cm>f>10cm,则f可能11cm或19cm,当f为11cm时,2f>12cm>f,成倒立放大的实像;当f为19cm时,12cm答案:C
思维拓展:当蜡烛距凸透镜30厘米时,在离该透镜40厘米的光屏上能成一个清晰的烛焰像;如果蜡烛到该透镜的距离为40厘米时,则在光屏上 ( )
A.一定成一个放大的像 B.一定成一个缩小的像
C.可能成一个倒立的像 D.可能不成像
解析:本题若用“不等式法”解题,也是能正确解答的,但较繁。建议利用“光路可逆法”解题,因为这样更简单。由题意可知,当物距u=30cm,像距v=40cm时,光屏上成清晰的像,因为物距小于像距,光屏的像一定是放大的,物距u应满足2f>30cm>f,像距v满足40cm>2f,当物距发生变化,变为40cm时,物距一定大于2f,故答案是唯一的,只能成“缩小倒立实像”。
答案:B
总结:解决以上有关问题,关键是熟记凸透镜成像的规律,每种情况下成像的性质是怎样的,这时物距、像距、焦距的关系怎样。另外,要养成仔细审题的习惯,要分清题目告知的是“物距”还是“像距”,才能正确找到切入点。
1.教学目标
知识与技能
过程与方法
能识别凸透镜和凹透镜
知道凸透镜的会聚作用和凹透镜的发散作用
知道透镜的主光轴、光心、焦点和焦距
理解凸透镜成像的初步规律
知道照相机、幻灯机、放大镜的成像原理
领会研究凸透镜成像的方法,感受验证过程的科学方法
学会验证凸透镜成像的规律
能运用凸透镜成像规律讨论、解决一些简单的实际问题
2.知识网络图
结构:中间厚、边缘薄
凸透镜
对光线的作用:会聚
(1)透镜 结构:中间薄、边缘厚
凹透镜
对光线的作用:发散
验证凸透镜成像的方法
成像规律 验证过程的科学方法
运用规律解决实际问题
(2)凸透镜成像
照相机
成像应用 幻灯机
放大镜
经典例题类析
[例题1] 完成图9中的光路图
?
解析:图9中所给的四个透镜,(a)、(b)是凸透镜,(c)、(d)为凹透镜,并且(a)、(c)给出入射光线,要求画出折射光线。而(b)、(d)则给出折射光线,要求画出入射光线。根据光心、焦点的定义方法就能画出这些特殊光线。
在画图中要注意光的传播方向。 (利用基本概念完成作图)
答案:如图10所示。
思维拓展:图11中正确表示了光通过透镜的是 ( )
A.甲图 B. 乙图 C.丙图 D.丁图
x*k.Com]
解析:根据凸透镜对光有会聚作用,凹透镜对光有发散作用,对比观察入射前和出射后光的变化情况。光通过甲图中的凸透镜(如图12所示)变得比原来会聚了,光通过乙图中的凹透镜变得比原来会聚了,光通过丙图中的凸透镜变得比原来发散了,光通过丁图中的凹透镜变得比原来会聚了。透镜对光的(明确会聚和发散的区别)“会聚”作用和“发散”作用并非只是针对平行于主轴的平行光而言,“会聚作用”应该理解为出射光比入射光会聚了一些;“发散作用”应该理解为出射光比入射光发散了一些。
答案:A
[例题2] 物体放在凸透镜的主光轴上,在距透镜40厘米处的光屏上得到一个倒立、放大的像,则该透镜的焦距可能为 ( )
A.40cm B.30cm C.20cm 10.5cm
解析:本题可以用“不等式法”来确定焦距的范围。根据题意“距透镜40厘米处的光屏”,可知像距v,且所得的像是倒立、放大的,根据凸透镜成像的规律得v>2f,即40厘米>2f,由此推得该凸透镜的焦距f<20厘米,符合这一要求的只有选项D。
答案:D
思维拓展1:物体距凸透镜20cm时,可在光屏上得到一个缩小的实像,若把物体向透镜方向移8cm,又可在光屏上得到一个放大的实像,则透镜的焦距是 ( )
A.20cm B.10cm C.9cm D.5cm
解析:根据题意,当物距u=20cm时,物体通过凸透镜在光屏上成倒立、缩小的实像。即物距必须满足u>2f,也就是f<10cm。这是焦距的第一个解。又从题意可知:把物体向透镜方向移8cm,所以当物距u=12cm时,物体通过凸透镜在光屏上成倒立、放大的实像。即物距必须满足2f>u>f,也就是2f>12cm>f ,求得12cm>f>6cm。这是焦距的第二个解。选取两个解的公共部分,求得最后结果为10cm>f>6cm。因此选C正确。
答案:C (注意:物体移动时的分析方法)
思维拓展2:物体距凸透镜30厘米时,在距透镜20厘米处的光屏上成一清晰的像,由此可以确定该凸透镜的焦距可能为 ( )
A.f=10cm B.f=15cm C.15cm>f>10cm D.无法确定
解析:本题有两种解法:
解法一:“不等式法”。由题意可知,光屏上成清晰的像,必定是实像,但到底是缩小的像还是放大的像,有的学生就分辨不清,故直接错选了“D”。其实物距30厘米大于像距20厘米,所以光屏上像是缩小的,物距30 cm>2f,求得f<15cm;而像距v满足:2f>20cm>f,求得20cm>f>10cm,取两个解的公共部分,得最后结果为15cm>f>10cm。因此选C正确。
解法二:“公式法”。根据题意,物距u=30cm时,像距v=20cm,直接带入凸透镜成像公式:1/u+ 1/v = 1/f,即1/30cm+1/20cm=1/f,求解得:f=12cm。因此选C正确。
答案:C(注意方法的灵活运用)
[例题3] 物体放在凸透镜前20厘米处,在透镜另一侧的光屏上成一个倒立放大的像。当物体距凸透镜12厘米时,所成的像 ( )
A.一定是倒立放大的实像 B.可能是倒立缩小的实像
C.可能是正立放大的虚像 D.可能是正立等大的虚像
解析:本题可以用“不等式法”先确定焦距的范围。由题意可知,当物距u=12cm时,物体通过凸透镜在光屏上成倒立放大的实像。即物距必须满足2f>u>f,也就是2f>20cm>f ,求得20cm>f>10cm。当物体离透镜12cm时,解题的关键是判断12cm与焦距f的关系,,较简单可行的方法是“特殊值法”。由于20cm>f>10cm,则f可能11cm或19cm,当f为11cm时,2f>12cm>f,成倒立放大的实像;当f为19cm时,12cm
思维拓展:当蜡烛距凸透镜30厘米时,在离该透镜40厘米的光屏上能成一个清晰的烛焰像;如果蜡烛到该透镜的距离为40厘米时,则在光屏上 ( )
A.一定成一个放大的像 B.一定成一个缩小的像
C.可能成一个倒立的像 D.可能不成像
解析:本题若用“不等式法”解题,也是能正确解答的,但较繁。建议利用“光路可逆法”解题,因为这样更简单。由题意可知,当物距u=30cm,像距v=40cm时,光屏上成清晰的像,因为物距小于像距,光屏的像一定是放大的,物距u应满足2f>30cm>f,像距v满足40cm>2f,当物距发生变化,变为40cm时,物距一定大于2f,故答案是唯一的,只能成“缩小倒立实像”。
答案:B
总结:解决以上有关问题,关键是熟记凸透镜成像的规律,每种情况下成像的性质是怎样的,这时物距、像距、焦距的关系怎样。另外,要养成仔细审题的习惯,要分清题目告知的是“物距”还是“像距”,才能正确找到切入点。
